S-GLCM熵：一种新的滚动轴承性能退化指标提取方法

潘玉娜，程道来，贾玉琛

（上海应用技术大学轨道交通学院，上海201418 ）

1 引言

随着科学技术的进步和工业的发展，旋转机械需要应对的工况越来越复杂。旋转机械在长期运行过程中，其关键零部件逐渐老化，使用寿命逐渐减少，发生机械故障的概率随之增加[1]。现有的机械设备维护方式主要分为定期维护和事后维修两大方法。事后维修是指机械设备在运行过程出现故障后才进行维修，虽然此种方法能够阻止设备故障进一步恶化，但是会造成不可避免的财产损失以及人员伤亡的风险。定期维修是指定期的对机械设备关键零部件进行检查、更换。这种方法虽然弥补了事后维修带来的财产损失以及人员伤亡的风险。但是当维修间隔设置不合理时，会产生维修不足或维修过剩问题，造成资源浪费，加大设备使用、维护成本。因此，对旋转机械重要部件进行可靠、全面的性能退化评估已成为设备状态监测领域的研究热点。寻找一种尽可能保持与性能退化过程一致并且对早期退化过程较为敏感的特征指标变得尤为重要[2]。

滚动轴承运行过程中产生的非高斯、非平稳性振动信号往往包含复杂的频率特征。S变换作为小波变换和短时傅里叶变换的继承与发展，具有良好的时频聚集性[3]。灰度共生矩阵能够通过研究灰度的空间相关特性来描述图像纹理[4]。信息熵作为一种度量信号复杂程度的方法，已经在性能退化评估中得到应用并取得了一定的效果[5-6]。滚动轴承信号经S 变换取其模后得到S时频谱图，通过灰度共生矩阵对S 变换时频谱图进行不同状态进行特征提取并对其进行复杂度度量，提出了一种S-GLCM熵特征指标来反映滚动轴承的退化过程。

2 S-GLCM熵

2.1 S变换

Stock well中提出了连续S变换定义[7]：

式中：f—频率；τ—时窗函数中心点。

由式（1）可以得出，S变换免去了窗函数选择的同时也改善了窗宽固定的缺陷，其高斯窗函数宽度与频率成反比，低频段时，时窗变宽，得到较高的频率分辨率，高频段时，时窗变窄，得到较高的时间分辨率，故S变换具有多分辨率的性质。

为了满足在计算机中对数字信号进行快速处理的要求，将连续S 变换通过快速傅里叶变换离散化后得到离散S 变换，当n≠0时表达式为：

当n=0时其离散S变换表达式为：

其中，T—被分析信号；x(t)—采样时间间隔，j，m，n=0，1，…，N-1。对被分析信号进行离散S 变换后得到复时频矩阵，列向量为某一时刻所有的频率展开，行向量为某一频率所有的时间点展开。

2.2 灰度共生矩阵

Haralick于1973年提出了灰度共生矩阵理论（GLCM，Gray Level Co-occurrence Matrix），是一种经典的图像纹理特征提取方法。GLCM是通过计算图像中一定距离和一定方向的两个矩阵元胞之间的灰度相关性，来表征图像灰度在相邻间隔、方向、变换快慢和幅度的综合信息。

设f(x，y)是某时频域的二维图像，取图像不同的两个点A，B，其中A点的坐标可描述为(e，f)，B点的坐标为(g，h)，两个点的位置方向为θ，两点距离为d。其中θ值取0°、45°、90°和135°（0°表示水平方向），记点对A(e，f)和B(g，h)在四个方向出现的概率为，即灰度共生矩阵：

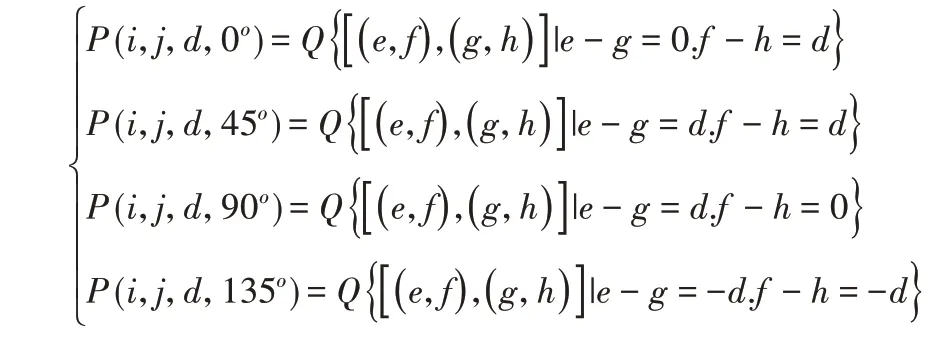
式中：Q—集合中的点对数量。

2.3 归一化信息熵

信息熵由C.E.Shannon于1948年提出，用来度量信息的不确定性[8]。其定义如下：已知一个信源由离散随机变量X={x1，x2，…xn} 组成，其概率分布函数为pi=P(xi)(i=1，2，…n)，则该信源的信息熵表示为：

因此，信息熵描述了信源中各个分量概率分布的均匀程度。各个分量分布越均匀，信息熵值越大，反之，信息熵值越小。但是信息熵的大小仅仅依赖各分量的概率分布，其取值范围为0～lnN，为了消除信源中分量长度的影响，采用下面的归一化形式：

从而使得信息熵的取值范围在［0，1］，有利于对信号进行定量分析和比较。

2.4 S-GLCM熵

GLCM可以分析图像的局部模式和排列规则等，但因其矩阵形式使得应用受限。往往将其进行二次特征提取得到二次统计量—熵特征。根据式（5）可得GLCM熵的定义为：

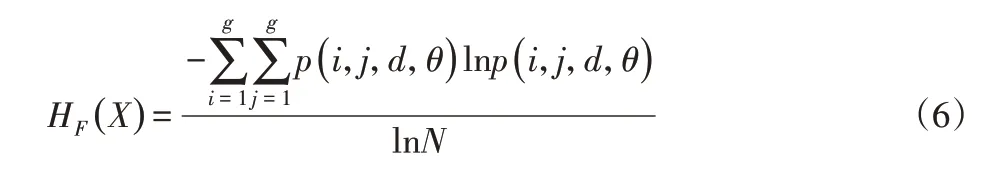
S变换时频谱图能够清晰有效的表征出滚动轴承不同阶段的差异性，提取S变换时频谱GLCM熵值特征作为滚动轴承的特征向量，记为：S-GLCM熵。

S-GLCM熵计算过程如下：

（1）对一个采样周期内采样数为n的信号X={x1，x2，…xn}进行S 变换，取其模得到S 变换时频谱系数矩阵。为一个n×n的矩阵，n为一个采样周期内连续时间信号x(t)的采样长度；

（3）对灰度共生矩阵P进行归一化信息熵特征提取。

S-GLCM熵同样满足信息熵的性质，各个分量分布越均匀，信息熵值越大，反之，信息熵值越小。

3 数学模型仿真分析

滚动轴承的损伤往往表现为内圈、外圈或滚动体上的局部点蚀。在轴承运转过程中，点蚀与其他组件不断接触时便会产生周期性的冲击，不同的点蚀故障产生的冲击频率不同，并且冲击幅值也会受到不同频率的调制，内圈故障受轴频调制，滚动体故障受保持架转频调制，外圈故障不存在调制。另外，在轴承运转过程中，滚动体和滚道间会存在微小的滑动。因此，滚动轴承故障模型[9-10]可表示为：

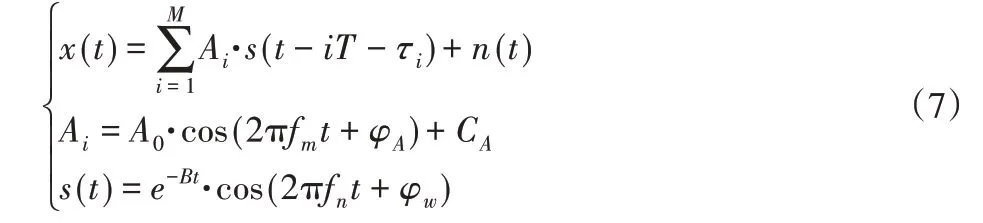
式中：fm—冲击幅值调制频率；A0—冲击强度；T—冲击周期；s(t)—平均周期为；T—共振衰减信号；τi—滚动体相对于滚道存在的随机微小滑动；n(t)—高斯噪声；fn—系统共振频率；B—共振衰减系数；CA—任意常数。

这里仿真信号轴承参数同下面的加速疲劳全寿命周期实验数据，即一个周期的数据长度2048，采样频率为25.6kHz，选取冲击强度A0数据为规律数据，即：A0=1，5，10。其他仿真参数：τi=0.02，fn=2000Hz，B=1000，加强性高斯白噪声的强度为0.4，当仿真内圈故障时，fm=fr，T=1/fip。当仿真外圈故障时，fm=0，T=1/fop。当仿真滚动体故障时，fm=fc，T=1/fbp。

对轴承滚动体损伤、内圈损伤、外圈损伤一个周期内的仿真信号的S-GLCM熵特征指标进行分析，如图1所示。由图1可知S-GLCM熵对于轴承滚动体、内圈、外圈不同程度损伤反应与理论分析一致：随着故障程度的加重，S-GLCM熵值减小。验证了S-GLCM熵的可行性。

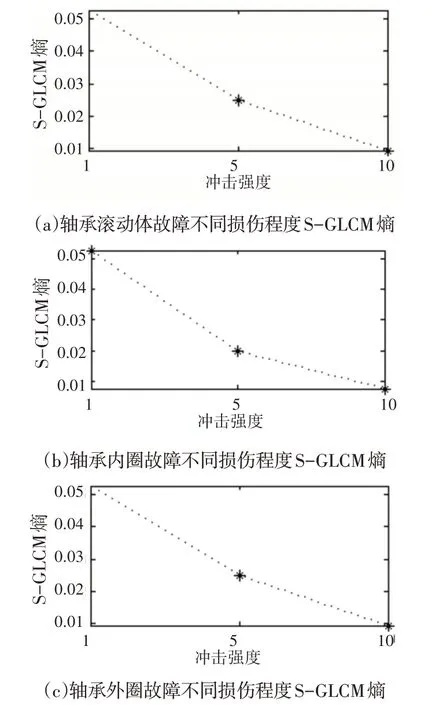
图1 轴承滚动体、内圈、外圈故障不同损伤程度S-GLCM熵指标Fig.1 S-GLCM Entropy Index of Different Damage Degree of Bearing Ball，Inner and Out

4 实验验证

轴承的实际性能退化是一个非常复杂的过程，数学模型仿真数据结果并不能有效地代表轴承在工程中实际的退化过程。因此文中采用上海交通大学机械与动力工程实验室滚动轴承加速疲劳全寿命周期的实验数据[11]对本文提出的方法进行了实验验证。轴承型号为6307，试验转速为3000rpm，荷载为，采样率为25.6kHz，每隔一分钟采一组长度为20480的数据。数据采集从轴承正常状态一直持续到寿命结束，两个轴承最终的失效形式都以内圈严重点蚀为主要因素。第一个轴承（记为B1）共采集了2469组数据，第二个轴承（记为B2）共采集了1062组数据。

有效值是目前工程上反映轴承全寿命退化过程中应用最为广泛也最为成熟的指标。因此，选取了有效值在全寿命周期中的变化情况与S-GLCM 熵在全寿命周期中的变化情况进行比较。首先对B1的有效值和S-GLCM熵进行对比分析。图2（其中(b)为(a)的局部放大图，下同）是B1全寿命周期内有效值的变化情况。从图中可以看出，有效值指标在1298min 左右有非常微弱的上升，可以认为此时是轴承开始出现轻微的损伤阶段，但有效值对此反映并不太敏感。在2308min 开始出现比较明显的上升，在2338min左右又一次出现大幅的上升后保持稳定，在失效时刻又大幅上升，可以认为是轴承损伤程度进一步恶化的两个阶段。图3是B1的S-GLCM熵在全寿命周期内的变化情况。从图中可以看出，在1294min对轴承出现轻微损伤的阶段有明显的反应，幅值出现大幅的上升，并在时间上与有效值相比有所提前。之后保持稳定，在2309min 开始出现明显的下降，并逐步下降，在2337min出现大幅下降，在失效时刻又出现较大降幅，对应了轴承损伤程度进一步恶化的两个阶段。

图2 B1全寿命周期有效值指标Fig.2 Full Life Cycle RMS Index of B1

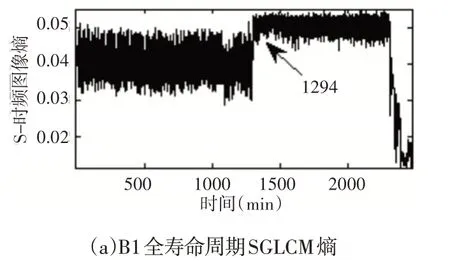
图3 B1全寿命周期S-GLCM熵指标Fig.3 Full Life Cycle S-GLCM Entropy Index of B1

为了验证文中所提指标的有效性，对B2的数据进行了同样的对比分析。B2的有效值在全寿命周期内的变化情况，如图4所示。从中可以看出，有效值在520min左右出现轻微幅值变化，之后保持稳定。在978min 开始出现比较明显的上升，在1040min左右出现大幅的上升直至失效时刻。B2的S-GLCM熵在全寿命周期内的变化情况，如图5所示。从图中可以看出，在513min左右出现较明显的上升，与有效值出现早期微弱故障阶段相对应，在时间上有所提前，并且S-GLCM熵增幅比有效值在此阶段增幅明显。之后保持稳定，在977min开始出现明显的下降，与其有效值出现故障加剧阶段相对应，并逐步下降，在1040分钟后出现大幅下降直至失效时刻，与其有效值出现大幅上升阶段相对应。

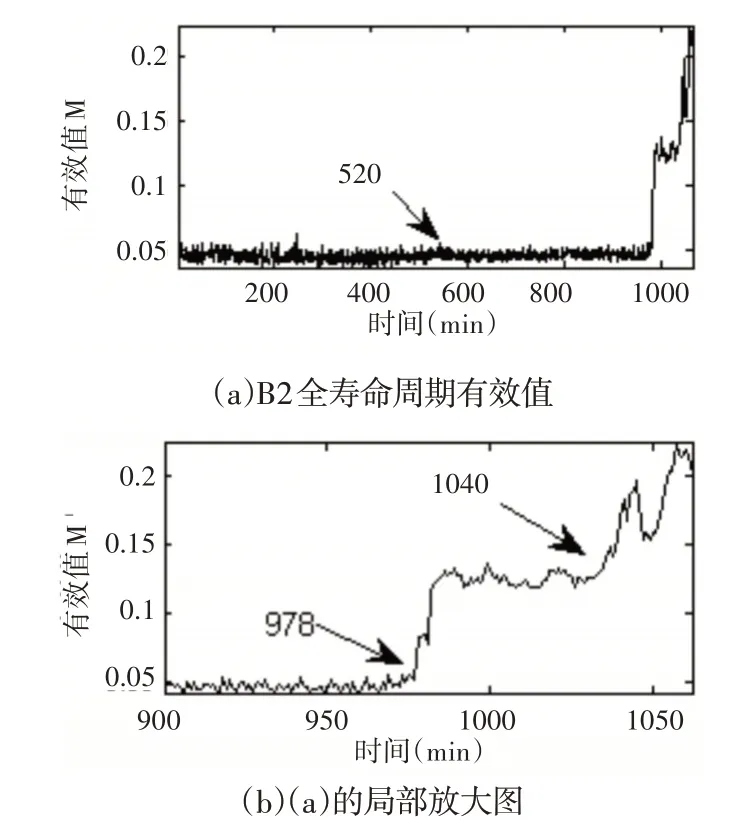
图4 B2全寿命周期有效值指标Fig.4 Full Life Cycle RMS Index of B2

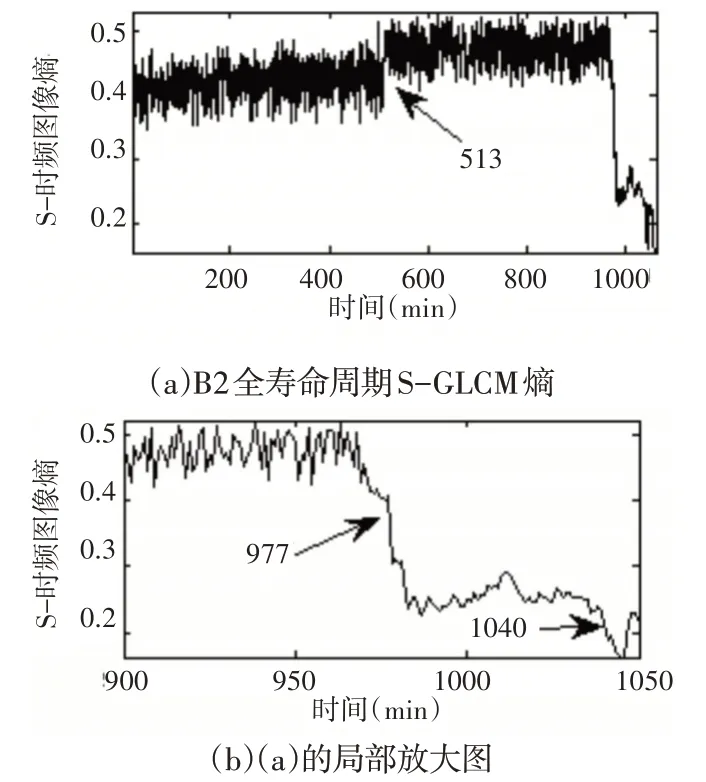
图5 B2全寿命周期S-GLCM熵指标Fig.5 Full Life Cycle S-GLCM Entropy Index of B2

为了更清晰的表现上述S-GLCM熵相对于有效值对轴承性能退化过程反映的优势，以及与仿真实验结果比较。将B1、B2两组轴承数据的S-GLCM熵和有效值对每个关键退化节点的表现时刻在表1中做出了详细对比。通过表1对比发现，B1、B2两组轴承数据在轴承开始出现轻微的损伤阶段，S-GLCM熵值均出现了明显的上升并在之后保持稳定的现象。文献[12]对本文数据进行了频谱分析，发现这可能是因为轴承在实际跑合过程中真实的损伤结果较为复杂，在出现轻微损伤后引起频率成分增加，主要的频率成分也集中到了（1000～4000）Hz，但频谱的复杂度反而下降，因此谱熵值也随之减小。在滚动轴承损伤加剧阶段，随着轴承损伤程度的加剧，其S-GLCM熵值减小，与数学模型仿真及人为损伤实验结果相对应。

表1 B1、B2故障状态对比表Tab.1 B1，B2 Fault Condition Comparison Table

通过上述实验验证和仿真结果验证对比分析得出：

（1）S-GLCM 熵对初始的退化表现敏感并且在时间上有所提前。在B1 轴承最初始的退化表现中相对于有效值提前了4min，并且幅值增幅明显。在B2轴承最初始的退化表现相对于有效值提前了7min，幅值增幅明显。

（2）S-GLCM 熵对轴承损伤进一步恶化的阶段也有良好的反应，相对于有效值反应时间有所提前，幅值下降明显。

综合来看，S-GLCM 熵对于滚动轴承全寿命周期中早期微弱故障阶段和故障恶化阶段都有着良好的反应。这对于在滚动轴承实际运行过程中有着很大的参考价值。

5 结论

从性能退化评估框架下特征指标相对匮乏这一研究现状出发，以深沟球轴承这一旋转机械中的关键零部件为研究对象，根据其振动信号的非平稳性。利用S变换这一具有良好时频聚集性的时频分析方法，通过GLCM 对S时频谱进行特征提取，结合信息熵能够定量度量信号分布均匀程度的特性，提出了S-GLCM熵的性能退化特征提取方法。通过对滚动轴承数学模型仿真信号分析验证了S-GLCM熵的可行性。通过对全寿命周期实验数据分析，由于轴承在实际运行中的复杂性，在出现微弱故障阶段其频率成分增加，熵值出现上升现象，相对于有效值在时间上均有所提前，幅值变化更加明显。在故障加剧阶段，相对于有效值在时间上均有所提前，幅值变化明显。结果表明，S-GLCM熵对深沟球轴承性能退化过程的反映相对有效值具有一定的优势，具有一定的理论意义和实际应用价值，可以作为性能退化评估框下现有指标的有益补充。