优化神经网络的锂电池SOC估算

刘晓悦，魏宇册

（华北理工大学电气工程学院，河北 唐山 063200）

1 引言

锂电池拥有蓄电量大、无记忆效应、质量轻、自放电率低、放电电压平稳、环境友好等诸多优点，因此成为车用动力电池首选[1]。但锂离子电池也带有明显缺陷，那就是对温度、电流和电压等有着苛刻要求，因而新能源汽车上需要配备电池管理系统（BMS）对电池进行实时监测和管控。SOC估计是BMS最为核心的技术。电池组的SOC是决定车辆接下来行驶里程和行驶性能的关键参数。电池组内部结构十分复杂，而且SOC与相关参数之间表现为高度非线性，导致建模困难，精准预测电池SOC成为亟待解决的一大难题。

以往对电池组SOC的研究基本是采用建立SOC与电池组的电流、电压、内阻等有关参数函数关系的方式，从而获得电池SOC值。放电实验法、电流积分法（AH法）、开路电压法、等效电路法、卡尔曼（Kalman）滤波法是常用的几种SOC 预测方法[2]。放电实验法能够获得不错的SOC预测结果，但实验时间太长。开路电压法能精准预测电池的初始数值，缺陷在于充放电时开路电压只能通过间接方式测量。卡尔曼滤波法预测精度有一定提高，该方法把电池看作一个动力系统，但该方法的准确性过度依赖于所建电池等效模型[3]。

上面提到的预测方法都兼具优缺点，因此有人采取组合的办法来预测电池SOC，提高SOC预测的准确性。文献[4]结合了扩展卡尔曼算法和安时法进行SOC 估算。文献[5]提出了一种融合安时法、开路电压法、卡尔曼滤波法的改进SOC方法，但电池SOC估算结果仍然无法满足电动汽车实际运行中SOC精度要求。锂电池在正常工作时可被看作是高度非线性的系统，而神经网络是一个非线性映射系统，并且不需要建立数学模型[6]，给定输入就能得到输出，可以很好地模拟电池动态特性。文献[7]利用BP神经网络估算SOC，文献[8]利用遗传算法优化的BP神经网络估算SOC都取得了较好的效果。但是鉴于一般的神经网络具有收敛速度慢、容易陷入极小值、预测精度不高等问题，本文提出用自适应变异粒子群优化算法对神经网络进行改进，提高SOC估计准确性。

2 自适应变异粒子群优化的BP神经网络

2.1 BP神经网络

BP神经网络是一种按照误差逆向传播算法训练的多层前馈神经网络，工作信号始终正向流动，没有反馈结构，在训练网络权值的过程当中，数据则沿着减少误差的方向传播。绝大多数人工神经网络都是采用这种网络及其变化形式。BP神经网络是包含多个隐含层的网络，具备处理线性不可分问题的能力。在保证网络性能和泛化能力的前提下，确定隐层层数的基本原则是：在满足精度的前提下尽可能取更紧凑的网络结构。网络性能与隐含层节点数关系，如表1所示。

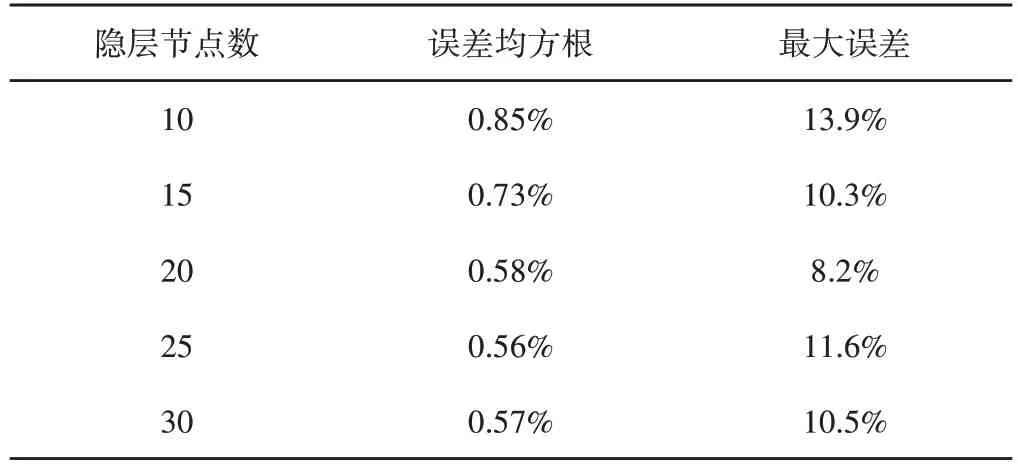
表1 网络性能与隐层节点数关系Tab.1 Relationship Between the Performance of Network with the Number of Hidden Layer Nodes

建立的就是基于改进BP神经网络的SOC估算模型。一个简单的3层BP神经网络，如图1所示。

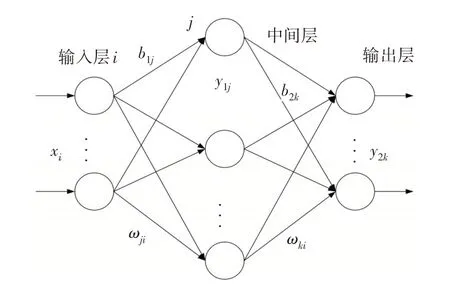
图1 BP神经网络结构Fig.1 The Structure of BP Neural Network

由于BP神经网络采用梯度下降法，所要优化的目标函数是非常复杂的，导致算法收敛速度慢、难跳出局部极小值的缺点。本文采用Levenberg-Marquardt算法来训练神经网络。

2.2 粒子群优化算法

粒子群优化算法（Particle Swarm Optimizition）是一种随机全局迭代进化算法，它速度快、算法容易、易于实现，需要调整的参数少，自提出以来得到了广泛的应用。粒子群优化算法初始化一群随机粒子，通过选取合适的目标函数为每个粒子分配适应度值，迭代环节过程中粒子利用个体极值P(best)和全局极值g(best)调整粒子本身的速度以及新的位置，并搜索当前最优粒子，反复迭代计算后，可找到待寻优函数的最优解集。自适应粒子群算法公式如下：

假设在一个D维的搜索空间内有n个粒子，每个粒子的速度根据（1）来计算。

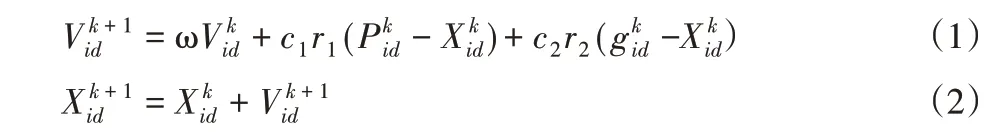
式中：ω—惯性权重；

d=1，2，…，D；i=1，2，…，n；

Vid—粒子速度；

Pid—粒子目前搜索到的最优位置；

gid—整个粒子群目前搜索到的最优位置；

k—当前迭代次数；

c1、c2—非负常数，称为加速度因子；

r1和r2—[0，1]之间的随机值。一般将粒子的速度和位置限制在区间，以防止粒子盲目搜索。

在式（2）中，ω为惯性权重，通常取较大值，ω的大小变化由最优适应值Q的变化来决定，两个变量之间的关系由下面两个公式表示：

式中：g(t)—种群的最优适应值；

r—均匀分布［0，1］之间的随机值；

Q—种群最优适应值的相对变化率；如图（4）所示，w的变化随着r值的变化而变化。

粒子群半径R与pgd和xid的关系如下，它表示种群内所有粒子到全局极值的最大空间距离：

式中：η—服从柯西分布函数的随机变量；

xid—编译后的xid数值；

xid—d维的数值。

处于全局最优位置的粒子从第n代进化到n+1代后，如果此时的P(n+1)适应度值比前一代更好，则用P(n+1)的适应度值代替P(n)的适应度值。反之，P(n)的值则保持不变，无法更新，算法则会选取不同的参数进行下一次进化，这样一直循环直至达到进化上限步数为止。

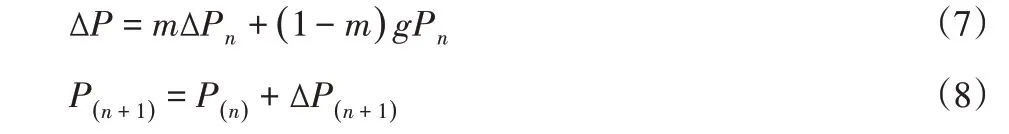
2.3 自适应变异粒子群优化算法

PSO 算法收敛速度很快，有很强的普适性，但容易提前收敛、局部寻优能力较差、收敛速度慢等不足，由于粒子群参数的初始化的算法具有随机性，而且太依赖于算法参数，从而导致寻优过程时间较长，容易出现早熟收敛和停滞。

另外，由式（1）可以看出，个体极值最优解Pid和群体极值最优解gid这两种因素会影响到每个粒子的运动状态。若这两个参数的最优解为同一个粒子，粒子则会以相同的轨迹向同一方向的同一点聚集，形成粒子种群的快速趋同效应，使粒子群高度集中，而导致搜索停滞不前，同时又使粒子间的相互学习减少，造成信息资源的浪费。面对这一现象，模仿遗传算法中变异思维，在算法中加入变异程序，按照一定的概率再次初始化部分粒子，增大找到全局最优解的几率。基于AMPSO 的BP 网络学习算法与标准BP 算法过程类似，只是在算法的过程中，要增加粒子群结点的初始化、结点位置向量变异及粒子群结点与BP 网络之间的相互映射等操作。

2.4 AMPSO-BP神经网络电池SOC估计模型

大量研究表明锂离子[9]电池组SOC受到电流、电压、温度等因素的影响。因此选择这3个变量作为神经网络输入，电池SOC值作为网络的输出。根据分析建立一个3-20-1 结构的网络模型。SOC预测流程，如图2所示。

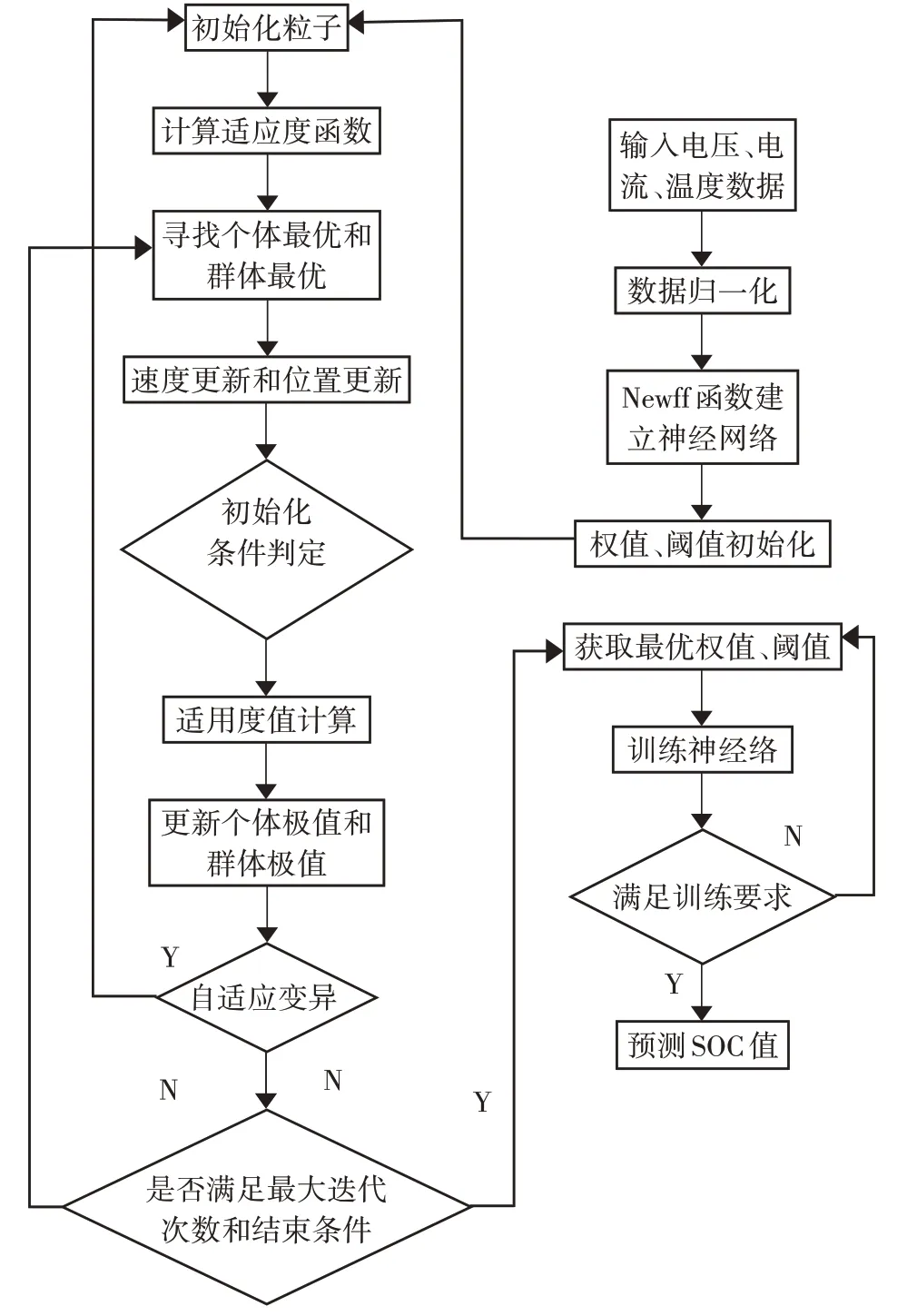
图2 AMPSO-BP SOC估算模型Fig.2 SOC Estimation Model Based on AMPSO-BP

3 实验仿真

3.1 实验参数设置

自适应变异粒子群优化算法种群规模M=20，最大迭代次数N=100，ω取值（0.3～0.8），学习因子c1、c2为1.4945，压缩因子α固定取值0.73。建立3-20-1 结构的BP 神经网络，训练方法采用Levenberg-Marquardt 优化算法。网络的训练函数为trainlm 函数，性能函数为MSE函数，学习率u=0.1，目标误差为0.00001，最大训练次数为1000次，其他参数均为缺省值。

3.2 训练神经网络

ADVISOR2002 是美国可再生能源实验室在MATLAB 和SIMULINK软件环境下开发的高级车辆仿真软件，可以对基本车辆，包括电动车辆的各方面性能进行灵活的建模和分析，ADVISOR[10]是一款分析性软件，简化了传统数学方法的建模过程，由于ADVISOR是模块化的，它的各种部件模型可以轻松扩展和改良。根据给定的道路循环条件，利用车辆各部分参数，用户可以对汽车的动力性、经济性等性能进行预测、分析与评估，以达到最终的要求。为了更好的估算锂电池SOC的实际应用，选取美国公司的GM_EV1型号的电动车，电池组容量为100Ah，锂离子电池总电压为344V（96节SAFT锂离子电池）。在BP神经网络模型的基础上，采用不同的SOC估算方法分析比较，模型1为扩展卡尔曼滤波器（EKF），模型2为无迹卡尔曼滤波器（UKF），模型3为标准粒子群优化算法（PSO），模型4为本文提出的自适应变异粒子群优化算法（AMPSO）。本实验测试样本为US06工况循环，电池组数据变化情况，如图3所示。测试样本为25个US06工况循环下完整电池组数据。

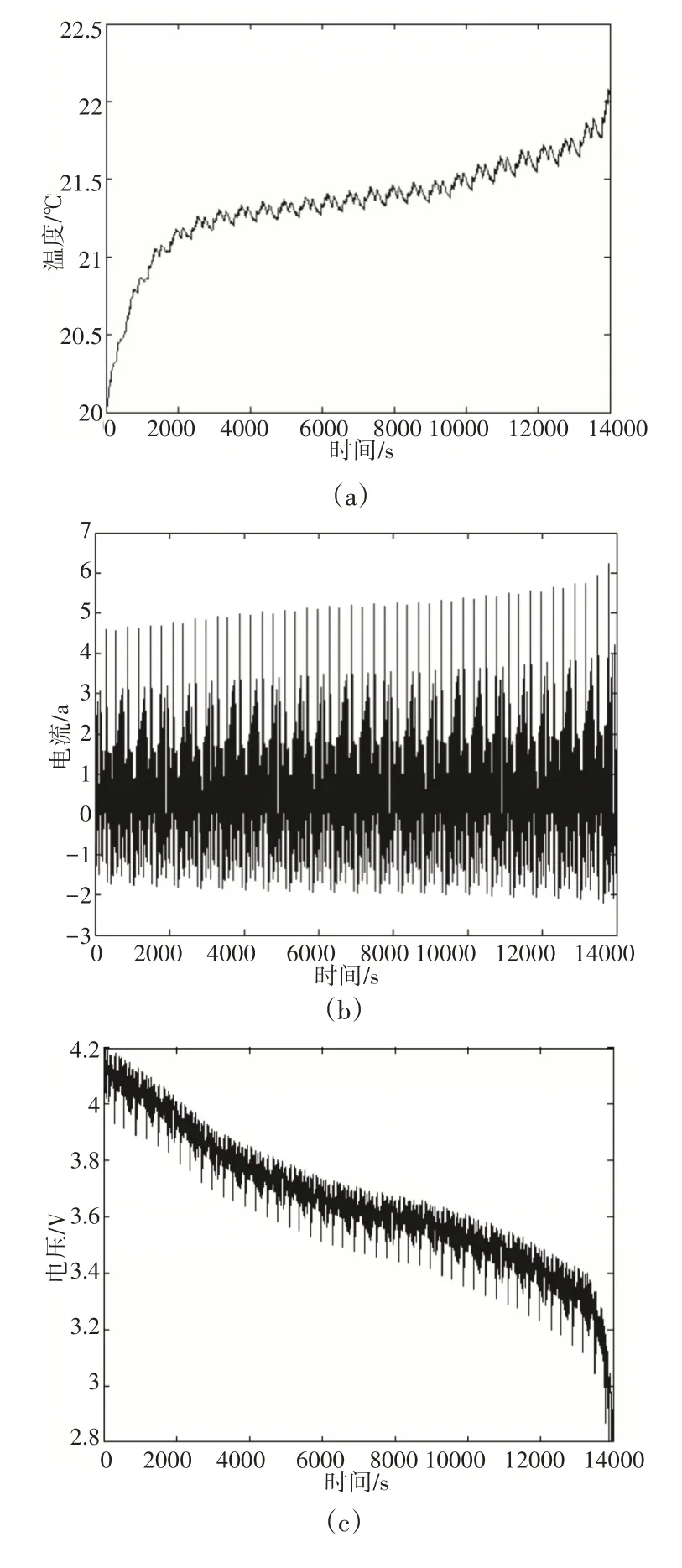
图3 US06工况下电池组数据Fig.3 Battery Pack Data Under US06 Conditions

3.3 神经网络预测结果

训练好神经网络后，利用US06工况数据进行SOC预测，4种模型误差对比，如图4所示。

图4 电池SOC估算结果对比Fig.4 Battery SOC Estimation Results Comparison

EKF、UKF、PSO、AMPSO四种SOC估算方法误差结果对比如图4所示，图中可以清晰的看出，AMPSO和PSO的估算效果明显优于UKF和EKF方法，AMPSO和PSO方法的收敛速度更快，EKF和UKF方法的误差波动变化大，不具有稳定性，AMPSO和PSO方法的预测曲线相对稳定，且最大误差均小于2%，而EKF方法的最大误差为3.09%，UKF方法的最大误差为2.48%。AMPSO与PSO的SOC估算的对比可看出，AMPSO方法的误差更小。为了验证实验结果准确性，进行多次试验，取平均结果，结果，如表2所示。

表2 SOC估算结果对比Tab.2 Comparison of SOC Estimates

4 结论

利用ADVISOR 提供的仿真电池组实际数据进行了SOC预测，对预测的结果进行了详细分析。采用自适应变异粒子群优化算法对BP 神经网络参数进行了优化，建立了AMPSO-BP 电池SOC 估算模型。结果表明，所提的AMPSO-BP 估算模型降低了传统BP神经网络的估算误差，有更高的预测精度和稳定性，是行之有效的SOC估算方法。