非线性负载下的微电网并联逆变系统谐波功率均分策略

张泽正，文传博

（上海电机学院电气学院，上海 201306）

0 引言

微电网可以将发电单元、负荷以及储能装置相结合，形成独立的供电系统[1]。在微电网孤岛运行过程中，常用下垂控制实现各逆变器的负荷分担，但用户侧大量非线性负载的接入，使系统产生谐波分量。而逆变器容量不同和线路组抗不匹配，导致系统中并联逆变器之间谐波电流无法实现均分，产生环流效应，进而增加电源、设备的负担以及线路损耗，影响微电网的可靠运行[2]。

目前，常用工频条件下的改进下垂控制实现对逆变器输出功率和系统电压的控制。文献[3]基于自适应虚拟阻抗的增强型比例功率分配策略，解决了复杂阻抗环境下的功率耦合，实现了基频条件下的功率分担。文献[4]在下垂控制策略中引入电压反馈环，实现了功率均分和稳压控制。文献[5]将IPSO算法和虚拟阻抗相结合，通过算法寻求耦合补偿中最优的参数，保证系统在稳定状态下运行。上述文献解决基频条件下的功率分担，但仍不能实现谐波功率均分。为了实现谐波频率下的均分控制，文献[6]提出了一种自适应虚拟谐波阻抗方法，实现了非线性负载下低次谐波均流过程，但没有针对高次谐波分配精度进行研究。文献[7]提出了一种分散分级控制方法，使用RBF神经网络进行计算，最终实现对谐波的均分控制，但其控制过程较为复杂，动态性能较差。文献[8]在谐波分频处理中加入高频频率信号，通过计算产生的谐波功率对虚拟阻抗进行动态调节，实现谐波功率的均分，但对于电压质量问题没有做出进一步的研究。

为了进一步提高接入非线性负载后微电网中谐波共享精度，在实现基频功率共享的前提下，本文通过提取不同频次的谐波电流并引入到控制策略中，将得到的谐波电压参考信号反馈到控制环，对谐波域输出阻抗进行整形，最终实现谐波功率均分。但由于引入谐波虚拟阻抗，可能导致母线电压谐波含量增加，因此本文提出电压谐波补偿策略，对公共点谐波电压进行适当的补偿，保证了公共点电压畸变在限制范围内。本文所提出的研究策略不仅能够实现不同谐波频率下的功率均分，提高谐波分配精度，同时还兼顾了谐波电压质量，解决了非线性负载接入造成的系统不稳定运行问题。

1 非线性负载下并联逆变器等效电路模型

常见的低压微电网中包括多个分布式电源，分布式电源经逆变器、滤波器以及传输线路向接入公共母线的负载供电。本文研究对象为两个逆变器并联系统，在微电网公共母线处接有线性负载和非线性负载。当非线性负载接入电网中，逆变器的输出电压、电流会发生严重畸变。为了便于分析，在谐波频率下，建立并联系统的等效电路模型，如图1所示。

图1 逆变器并联谐波等效电路Fig.1 Equivalent circuit of parallel harmonics of inverter

图中：将非线性负载的谐波成分等效为电流源ih，上标h表示谐波次数。Zinv为逆变器的等效输出阻抗；ZLh为谐波频率下逆变器接口到母线处的线路阻抗；Vpcch为谐波频率下的公共点电压幅值；io1h，io2h分别为逆变器1，2输出的谐波电流。

由图1可得，谐波频率下公共点电压为

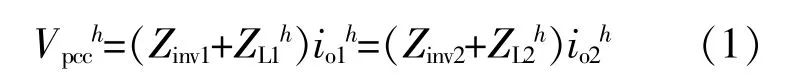
由于系统中线路阻抗远大于逆变器的等效输出阻抗，逆变器输出的谐波电流可表示为

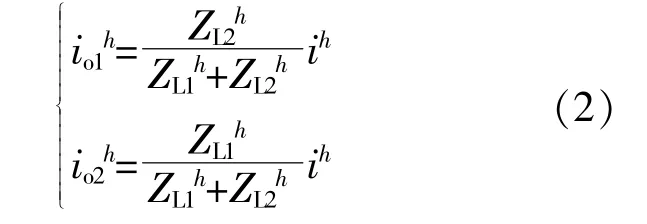
由式（2）可以看出，当逆变器到公共母线的线路阻抗不匹配时，其谐波频率下的电流会根据线路阻抗进行分配，进而产生环流，谐波功率不能实现均分，对系统的稳定运行造成影响。当某一逆变器承受谐波电流较大时，可能会超出逆变器承受限定值，造成设备损坏或过热。

2 逆变器功率均分控制

上文对于非线性负载引入所带来的环流效应进行了分析，通过改变逆变器到公共母线的等效输出阻抗实现谐波功率的共享，进而消除逆变器的环流。因此，为了实现逆变器之间的均流效果，可通过引入谐波虚拟阻抗，使等效输出阻抗相等，即：

式中：ZV1h，ZV2h为逆变器的谐波虚拟阻抗。

引入固定谐波虚拟阻抗可以整定系统的谐波输出阻抗，实现谐波功率均分[8]。但由于固定的谐波阻抗须要测量线路阻抗值，且为了削弱线路阻抗不匹配所带来的影响，常须要满足ZVh＞＞ZL，不适用于多个逆变器并联的复杂网络。

2.1 基频下的功率控制

在微电网的控制中，常采用下垂控制实现基频条件下逆变器功率和电压幅值的控制，考虑到低压微电网线路中阻性成分远大于感性成分，因此采用下垂控制公式：

式中：下标n为第n台逆变器；Pn和Pn*分别为逆变器的额定有功功率和实际输出有功功率；Qn和Qn*分别为逆变器的额定无功功率和实际输出无功功率；ωn和ω0分别为额定角频率和角频率参考值；U0为逆变器的额定电压幅值；Un为逆变器电压幅值的参考值；m和n为下垂控制系数。

2.2 谐波功率均分控制

为了实现谐波功率均分控制，首先提取逆变器输出电流，对电流进行分频谐波处理，由于本文建立的微电网模型为三相三线制模型，负载对称，因此不考虑偶次谐波的影响。其谐波功率均分策略如图2所示。

图2 谐波功率控制流程图Fig.2 Flow chart of harmonic power control

图中：Vo，io分别为逆变器的输出电压和电流；ωh为h次额定角频率；inh为提取出的h次谐波电流；Qnh为h次谐波无功功率；Qrate为引入的谐波无功功率参考值；Vreff，Vrefh分别为下垂控制得到的基波电压参考值和h次谐波频率下的电压参考值；VVh为计算所得的h次谐波虚拟电压；Vref为送入电压电流环的电压参考值。

由图2可得，采用双二阶广义积分模块对谐波电流进行提取，将提取出的h次谐波送入谐波无功功率计算模块，得到h次频率下的谐波无功功率，其功率表达式为

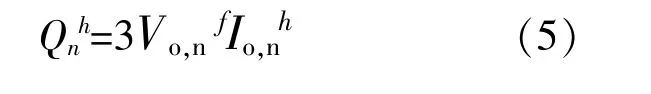
式中：Vo，nf为基频下的逆变器输出电压幅值；Io，nh为逆变器输出的h次谐波电流。

由于下垂控制特性，基频下的输出电压偏移量很小（不超过5%），因此，谐波功率的产生主要取决于谐波电流。为了实现精确的谐波功率共享，在线路阻抗和负载电流未知的情况下，设计谐波虚拟阻抗计算过程为

式中：kh为谐波系数。

由于谐波虚拟电压与谐波虚拟阻抗成正比，可将计算出的谐波虚拟电压值引入电压电流环进行进一步的控制，其计算过程如图3所示。

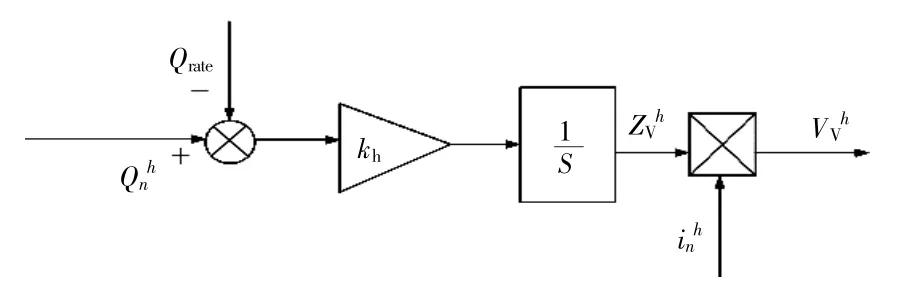
图3 谐波虚拟电压计算结构图Fig.3 Structure diagram of harmonic virtual voltage calculation

其设计的主要思路：当逆变器之间产生谐波环流时，谐波功率无法达到均分状态，假设线路阻抗ZL1＞ZL2，此时io1h＜io2h，可得Q1h＜Q2h，根据式（6）计算，得到谐波功率初始参考值，进而得到的初始谐波虚拟阻抗ZV1h＜ZV2h。通过实时变化的谐波功率有效值来构造变化的谐波虚拟阻抗，对不同频次下的系统阻抗进行自适应补偿，从而改变系统谐波域的阻抗特性，进一步改善谐波环流的均分精度。将得到的电压参考信号反馈到电压电流环，可以改变逆变器的输出电压电流。

根据前文的分析，在引入谐波虚拟阻抗后，逆变器间的环流为

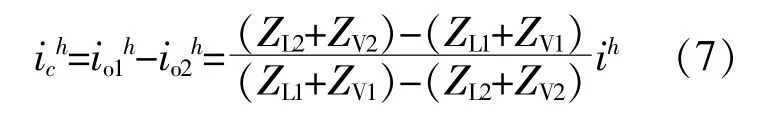
承担谐波电流较大的逆变器，根据式（6）的调节可以添加较小的谐波虚拟阻抗值，随着谐波功率的变化，当ZL1+ZV1=ZL2+ZV2时，谐波环流为0，系统达到稳定状态，此时积分器输入在稳态情况下为0，各逆变器须满足：

由式（8）可得，当系统达到稳定状态时，对于容量不同的逆变器，可通过设计其谐波系数与容量呈反比，即可实现谐波功率均分。

3 电压谐波补偿策略

由于引入谐波虚拟阻抗，逆变器的等效输出阻抗发生改变，此时新的公共点谐波电压为

由式（9）可知，谐波虚拟阻抗的引入，导致PCC点的电压谐波含量增大，谐波畸变率增加。为了保证电压质量，进一步补偿公共点电压谐波，本文提出了电压谐波补偿策略，引入新的电压参考量，其表达式为[9]～[11]

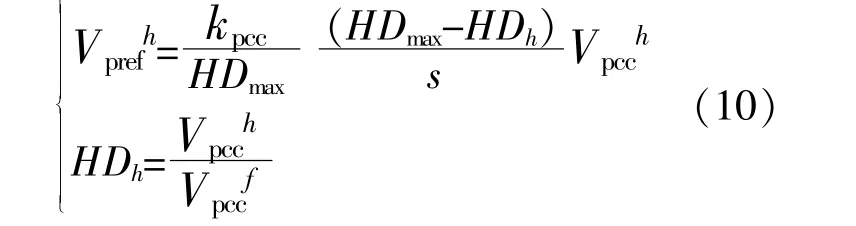
式中：kpcc为电压谐波补偿系数；HDmax为各频次电压谐波畸变最大参考值；Vpccf，Vpcch分别为公共母线处基频和h次谐波电压幅值。

将采集到的母线电压通过分频处理，提取基频公共点电压和不同频次的谐波电压，引入电压谐波补偿模块，得到公共点谐波电压参考值Vprefh，将其送入电压电流控制环，即可得到补偿后的分量。电压谐波补偿策略如图4所示。

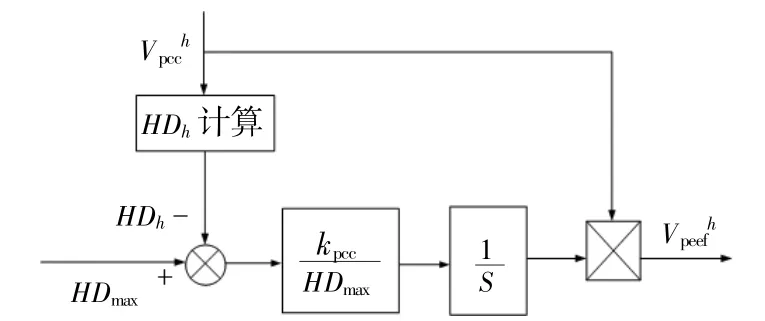
图4 电压谐波补偿策略控制图Fig.4 Control diagram of voltage harmonic compensation strategy

由图4可知，引入后修正的电压参考值为

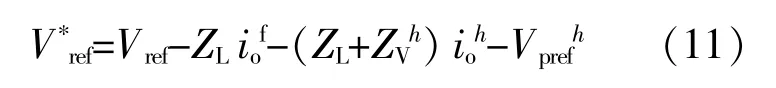
由式（11）可知，引入谐波虚拟阻抗仅改变不同谐波频率的等效输出阻抗，对基频条件下的电压参考值不会产生影响。

为了实现对各频次信号的跟踪，在电压环控制中采用基波比例谐振控制器和多个谐波谐振控制器，电流环采用比例调节器，为LC滤波器提供足够的阻尼，其具体的传递函数为

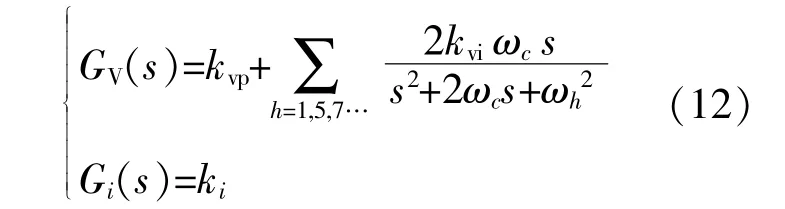
式中：kvp，kvi分别为电压环的比例系数和谐振系数；ωc为截止频率；ki为电流环的比例系数。

4 仿真及结果分析

为了验证本文所提出谐波功率均分和电压谐波补偿策略的有效性，在Matlab/Simulink中搭建了以两个逆变器为基础的微电网并联逆变系统，在公共母线处接有线性负载和非线性负载，其中，线性负载为有功功率为2 kW、无功功率为1 kVar的恒功率负载，非线性负载为二极管整流器，输出端电阻为30Ω，基频频率设置为50 Hz。仿真参数见表1。仿真过程主要验证5，7，11次谐波均分状态及公共母线电压谐波畸变率变化，仿真时间设置为1.8 s，仿真结果如图5所示。

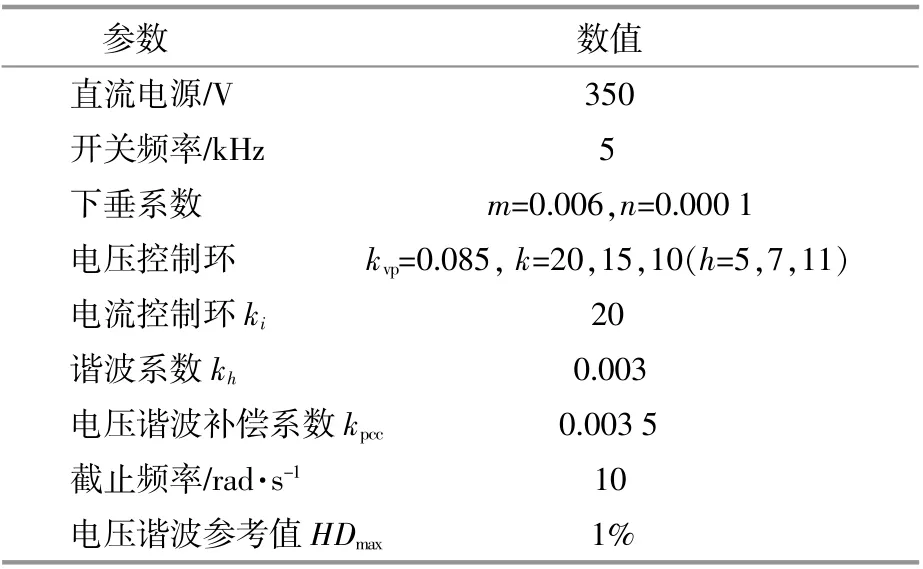
表1 仿真参数Table 1 Simulation parameters

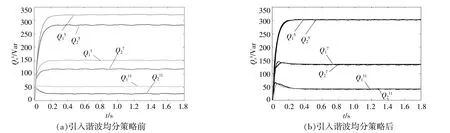
图5 引入谐波功率均分前后并联逆变器谐波功率波形图Fig.5 Harmonic power waveforms of parallel inverters before and after the introduction of harmonic power sharing

由图5可知，未采用谐波功率均分策略前，在经过短暂的瞬态过程后，仅在传统下垂控制下，虽然谐波功率最终趋于稳定，但逆变器之间的谐波功率不能实现均分，这必然导致系统中产生环流，系统不能稳定运行。引入谐波功率均分策略后，系统中5，7，11次谐波功率均分状态，并为了测试系统的动态响应，在t=1 s时接入新的负荷。在系统运行约0.2 s后，逆变器的5，7，11次谐波功率基本达到均分状态，并实现稳定。负荷发生变动后，经短暂的瞬态响应，谐波功率仍保持均分状态，验证了所提出的谐波功率均分策略的有效性。

为了进一步验证谐波功率均分策略在多个逆变器并联系统中的有效性，在上述算例基础上并联同等容量的逆变器3，分别设置不同的线路阻抗值，对比策略引入前后谐波功率的均分情况，如图6所示。

图6 引入谐波功率均分前后多逆变器并联谐波功率波形图Fig.6 Waveforms of harmonic power of multiple inverters connected in parallel before and afterthe introduction of harmonic power sharing

由图6可知，尽管系统为馈线阻抗不匹配的多逆变器并联系统，但在引入谐波功率均分策略后，系统中各逆变器仍能实现不同频次的谐波功率均分。

以逆变器1，2为例，观察逆变器之间环流特性如图7所示。

图7 引入谐波功率均分前后A相负载电流波形Fig.7 A-phase load current waveform before and after the introduction of harmonic power sharing

由图7可知：在系统引入谐波功率均分策略前，逆变器1，2的A相负载电流波形均存在畸变，且谐波不能实现均分，存在较大的谐波环流；在系统引入谐波功率均分策略后，谐波虚拟阻抗跟随谐波功率变化，稳定状态下谐波环流明显减小，更接近于0，此时逆变器1，2的谐波电流近似于均分状态，因此谐波功率可实现均分。

本文分别对引入电压谐波补偿策略前、后的公共点电压波形和频谱进行分析，其结果如图8，9所示。

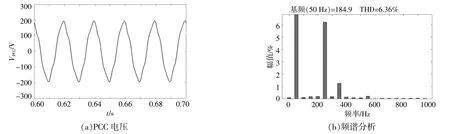
图8 引入补偿策略前的公共点电压波形和频谱分析Fig.8 Analysis of voltage waveform and spectrum of common point before introducing compensation strategy

图9 引入补偿策略后的公共点电压波形和频谱分析Fig.9 Analysis of voltage waveform and spectrum of common point after introducing compensation strategy

由图8，9可知：系统达到稳定状态后，在引入补偿策略前，公共点电压波形具有明显畸变，总畸变率THD达到了6.36%，高于电网要求的5%，且频谱分析中5，7次谐波均超过了规定的电压谐波允许的最大值，电压质量较差；在引入电压谐波补偿策略后，电压波形得到了明显改善，电压THD由6.36%降到了1.01%，符合电网要求，且选取的5，7，11次谐波占比均未超过1%，由此证明电压谐波补偿策略的有效性。

5 结论

本文针对低压微电网中公共母线接入大量非线性负载，导致系统中谐波含量增加，且谐波不能实现均分而导致系统中存在环流，电压质量降低等问题进行了分析，并提出了谐波功率均分策略以及公共点电压谐波补偿策略。通过自适应跟随谐波功率变化，引入谐波虚拟阻抗，解决由于复杂的微电网结构及馈线阻抗不匹配而导致的环流问题，使谐波频率下等效输出阻抗近似相等，最终实现谐波功率均分，降低系统中的环流。同时，所提出的电压谐波补偿策略，有效地降低了电压谐波畸变率，满足电网对于电压质量的要求。仿真结果验证了所提出策略的有效性。由于本文策略的实现须要提取不同频次的谐波电流，设计结构更加复杂，对精度和动态性能要求更高，简化结构设计，减小硬件误差是所提控制方法今后研究的重点。