基于AP算法的路网同质区域划分方法研究

郭红莉，刘晓雯，种潇敏，曲卫东

(长安大学 信息工程学院，陕西 西安 710064)

0 引 言

交通作为城市的重要组成部分，为城市经济的快速发展做出了巨大贡献，也在很大程度上促进了社会的进步。但是随着城市规模的不断扩大和城市化进程的加快，同时也导致了汽车的保有量急剧增长，城市的交通拥堵问题日益严峻。机动车保有量的快速增长给城市交通运行带来了很大的压力，严重影响了城市交通系统的正常运转，并在一定程度上限制了社会经济的稳定发展。同时交通拥堵所引发的经济损失、交通事故等后果对城市居民和社会造成了很多负面影响，因此如何缓解交通拥堵问题成为当今的热点研究方向之一。对城市路网进行合理的分区，有助于提高道路交通的运行效率。挖掘城市路网交通信息并对路网进行分区，降低路网复杂性成为智能交通领域中的一个重要研究方向。这些研究可以更好地发现城市交通内部的运行规律，从而为交通管理者制定交通拥堵缓解措施提供有力的理论依据。

目前，许多国内外研究者都认识到区域划分在智能交通领域研究中的重要意义，并对路网区域划分方面进行了大量的探索和研究。例如Geroliminis等人利用指数族函数对仿真数据进行回归分析，并基于3D-vMFD、3D-pMFD提出了一种新的交通区域划分方法[1]。Wang等人首先使用改进的C均值算法评价交叉口在交通路网中的重要性，然后选择几个关键路口将路网划分成几个不同的子区域，并最终达到了对路网的合理分区和控制[2]。尹洪英等人基于路网交叉口的拓扑特性和实时交通流数据构建了相似性矩阵，并采用谱聚类算法结合谱图理论对路网进行动态划分[3]。吕玉强等人以聚类算法为基础，通过对比和交通区域划分的相似性，利用K-means空间聚类法对交通区域进行划分[4]。Saeedmanesh等人通过在路网中迭代计算，获得局部性质相似的路段，然后采用对称正定矩阵因式分解获得较高相似性的集群，从而获得路网的同质区域并实现区域的划分[5]。冯树民等人考虑路网区域之间的相似性和位置关系，使用两维图论聚类方法对交通区域进行划分，能够有效克服现有方法无法识别交通区域位置关系的缺点，并在此基础上对区域进行合并[6]。

从国内外研究可以看出，交通区域划分多基于聚类方法对路网宏观交通状态进行划分，大多数划分算法存在着初始值敏感性及聚类个数的设定问题。同时，如今国内外基于路网同质区域划分的研究比较少，因此文中采用AP算法对路网进行同质区域划分，该方法与现有的方法相比优势在于它可以很好地挖掘出城市路网中的瓶颈路段和敏感节点，并且具有很好的稳定性、可靠性和高效性，从而有助于交通部门针对道路改造、交通诱导和交通规划方面做一些措施以进一步改善交通拥堵问题。

1 AP算法原理

AP算法[7]是Frey等人于2007年在Science杂志中的“Clustering by Passing Messages Between Data Points”一文中提出的一种基于数据点间“信息传递”的新聚类算法，因其具有高效、稳定等特点，被广泛应用于各大领域。并且AP算法不需要事先确定聚类中心和聚类个数，而是将所有样本点都看作潜在的聚类中心，通过循环迭代，在迭代过程中不断搜索合适的聚类中心，自动从数据点间识别聚类中心的位置及个数[8]。

AP算法的基本思想是基于网络中数据点与数据点之间进行的消息传递[9]，将整个数据集合看作网络，其中将各个数据点看作网络中的节点，然后通过网络中各条边的消息传递进而寻找数据点与聚类中心之间的隶属关系，从而实现数据间的自适应聚类。AP算法首先计算数据点间的相似度矩阵s，将任意两个数据点i与j之间的相似度值定义为s(i,j)，一般将其设置为一个负的平方差值(欧氏距离的负数)，其计算公式为：

s(i,j)=-d2(xi,xj)=-|xi-xj|2,i≠j

(1)

在相似度矩阵中，对角线上的数值s(i,i)作为某点能否成为聚类中心的评判标准，这个值称为参考度p，调节p值可以改变某点成为聚类中心的概率，p值越大则证明该数据点成为聚类中心的概率越大。在消息传递之前，通常认为所有的数据点都同等地适合作为聚类中心，因此p值的选取一般为相似度矩阵的中心值(结果产生聚类中心的数量较合适)或相似度矩阵的最小值(结果产生聚类中心的数量较少)，但也可以根据实际情况来设定。p值通过以下公式计算：

(2)

为了找到合适的聚类中心，AP算法通过迭代不断地更新相似度矩阵中每个数据点的吸引度值和归属度值，直到找到最合适的聚类中心，然后将网络中其余的数据点分配到相应的簇中。算法通过r(i,k)+a(i,k)的值来确定聚类中心点，r(i,k)+a(i,k)的值越大，则k最终作为聚类中心的可能性越大。算法迭代之前，将吸引度矩阵R和归属度矩阵A都初始化为0矩阵，并使用以下公式迭代计算：

(3)

at+1(i,k)=min(0,rt(k,k)+

(4)

(5)

其中，r(i,k)为吸引度信息，表示点i选择点k的过程；a(i,k)为归属度信息，表示点k选择点i的过程。

算法在传递消息的过程中，可能会由于数据震荡影响最终聚类结果，因此在更新信息的过程中引入阻尼系数λ，其值在0和1之间。迭代公式为：

rt+1(i,k)=(1-λ)rt+1(i,k)+λrt(i,k)

(6)

at+1(i,k)=(1-λ)at+1(i,k)+λat(i,k)

(7)

迭代完成后，根据吸引度值和归属度值来得到最终的聚类中心点，不论是否k=i，对于点i来说，使得r(i,k)+a(i,k)取最大值的那个k即为点i的聚类中心。当算法的迭代次数达到设定阈值或经过若干次迭代后其聚类中心保持不变时，则消息传递过程终止，算法结束。

2 路网同质区域划分

道路交通网络不仅要考虑路网的拓扑结构，还要考虑路网本身的交通特性[10]。城市路网的拓扑特性与交通流的周期相似特性揭示着路网中存在同质的区域。路网的同质区域是指路网中交通流在一段时间内具有规律变化的相似性的区域。首先对交通时间序列数据进行聚类分析，然后得到交通状态变化的同质区域并挖掘出路网中的瓶颈路段和敏感节点。发现和挖掘出这些同质区域对于局部区域实施灵活的协调控制方案、保证交通控制系统的可靠性等方面有很大作用，不同同质区域间的交通状态变化情况还可以很好地帮助我们分析出路网结构的脆弱性，挖掘出路网的敏感交叉点。文中主要关注路网宏观同质区域的划分。

2.1 数据预处理

文中实验数据来自于陕西省西安市二环区域内的13 000辆出租车运行的GPS数据，每日采集数据条目数约为2 700万条，浮动车系统每隔30秒更新一次数据。由于出租车采集到的GPS数据均为没有经过处理的原始数据，这些数据可能受到定位设备或外部因素的影响，导致其内容和准确性存在部分的偏差和错误[11]。数据筛选和处理的目的是为了去除错误数据和研究范围之外的数据。对出租车GPS数据做了如下分类和相应处理：

(1)数据冗余。若数据表中有多条相同记录则只保留其中一条，其余记录全部删除。

(2)数据错误。若数据表中某个字段的属性值超出合理范围，如经纬度、速度等字段，则删除此类数据。

(3)数据失效。文中是对15分钟内的交通状态分析，所以筛选出速度字段连续15分钟取值为0的数据条目并将其删除。

(4)坐标纠偏。在将出租车GPS坐标匹配城市路网之前，针对出租车GPS数据的偏移情况，将出租车GPS数据坐标系与路网坐标系统一转换为WGS-84坐标系。

GPS数据做以上处理之后，文中选择西安市内交通状态变化较复杂的二环区域作为研究对象。由于城市路网是一个具有离散性、强耦合性和非线性的复杂网络，所以首先要将真实的城市路网抽象成拓扑结构图[12]。通过标记西安市二环区域内的交叉点经纬度坐标来构建城市路网的拓扑结构图，然后通过计算西安市13 000辆浮动车在工作日各区域路段不同时间段内的平均速度，对城市路网的各个区域拥堵情况进行划分。采用国内最常用的B类城市的标准，即公安部新修订的《城市道路交通管理评价指标体系》中的规定来判别交通状态。该指标根据城市主干道路车辆的平均速度定义道路的拥堵程度，并将交通状态划分为五个等级，分别是畅通、基本畅通、轻度拥堵、中度拥堵和严重拥堵，同时规定了各自的速度阈值[13-14]。当平均速度大于等于28 km/h时为畅通状态，当平均速度位于25 km/h和28 km/h之间时为基本畅通状态，当平均速度位于22 km/h和25 km/h之间时为轻度拥堵状态，当平均速度位于19 km/h和22 km/h之间时为中度拥堵状态，平均速度小于19 km/h时为严重拥堵状态。

2.2 时间序列数据的相似性度量

时间序列数据是按照时间顺序排列的数据序列，可以潜在地表达数据内部状态随时间变化的规律，交通流是典型的时间序列数据。对时间序列数据进行分析，挖掘其内部规律在各个领域应用广泛。文中以西安市二环区域内某工作日6:00到22:00这一时间段内的189条路段的出租车为研究对象，每隔15分钟计算一次各路段出租车的平均速度作为时间序列数据。

时间序列数据在进行聚类分析之前，通常需要计算样本之间的相似度。对于很多的机器学习算法来说，选择一种合适的相似性度量方法评价数据之间的相似性对这些算法的性能有非常重要的影响。相似性度量[15]指的是样本之间相似性程度的一种度量，然后根据数据点间的相似度，将时间序列数据集划分为多个类别。时间序列的相似性度量通常采用衡量两个不同时间序列之间距离远近程度的方式来验证两个序列是否相似[16]。聚类算法在数据挖掘领域应用广泛，在应用于时间序列数据挖掘领域时，一般会与相似性度量相结合[17]。相似性度量的目的在于计算、衡量空间中样本点间的相似性。文中采用的时间序列数据是等长的，而动态时间规整距离(DTW)主要用于解决两个不等长的时间序列进行相似性对比的问题，并且DTW距离需要计算累加矩阵及最优规整路径，所以复杂度较高且对数据点变化敏感，因此选用欧氏距离作为相似性度量的方法。

2.3 算法设计及流程

文中研究的数据为在工作日内预处理后的(6:00至22:00)189条路段的时间序列数据，然后采用欧氏距离计算每两条路段之间的相似度值并构建相似度矩阵。

基于AP算法的路网同质区域划分步骤如下：

步骤1：首先使用欧氏距离作为相似性度量方法计算189条路段时间序列数据的相似性；

步骤2：将建立的时间序列相似度矩阵作为本次聚类的输入数据集；

步骤3：选择相似度矩阵的均值作为参考度p的值，来得到合适的聚类个数；

步骤4：算法初始化，迭代更新吸引度矩阵R(189*189)和归属度矩阵A(189*189)；

步骤5：当聚类中心稳定或迭代次数达到设定阈值时，会生成最终聚类中心点，并根据聚类中心与其他点的相似程度将数据集划分为不同的类别。

算法实现流程如图1所示。

3 实验结果分析

3.1 路网同质区域划分

路网全天交通状态变化同质区域划分的可视化结果如图2所示。同质区域的道路采用同一种灰度表示，不同灰度代表了路网各个区域一天内的交通拥堵程度，其中，灰度由深到浅依次表示为严重拥堵区域、畅通区域、基本畅通区域、中度拥堵区域和轻度拥堵区域。

从图2中可以看出，通过对相似性路段进行聚类可以很好地发现路网中交通状态变化的同质区域，并且可以看出路网中全天处于严重拥堵或者高峰时段严重拥堵的道路大多集中在西安市的核心区域附近。

图1 路网区域划分流程

图2 路网同质区域划分

道路时间序列变化的谱图如图3所示，其不同灰度表示道路的拥堵程度。从以下谱图可以看出，从早6:00到晚10:00这一时间段内，第一、二类道路处于基本畅通状态，第三、四、五类路网子区域的周期变化和潮汐交通现象逐渐明显，第六类则全天多处于严重拥堵状态。从谱图中还可看出全天路网中道路状态的变化情况，路网中同质区域内路段的交通状态变化规律基本一致，交通部门可以根据这些变化规律做出一些交通诱导。这种同质的变化规律能很好地对该区域进行交通信号控制、道路改造及交通诱导指挥，同时也减少了一些不必要的交通疏导，从而能够更加有效地对拥堵区域进行交通疏导工作，提高城市交通运行的效率和可靠性，进一步缓解交通拥堵问题。同时也为城市的智能交通控制和交通信息诱导提供理论支撑。

3.2 路网脆弱性的识别

通过对路网中同质区域的划分和其全天的交通状态情况还可以很好地帮我们挖掘出路网结构的特性。当交叉点邻接多个不同的同质区域时，由于受到多个不同交通状态的影响，交叉点的控制就显得格外重要。图4中分别标记出了部分瓶颈路段和敏感节点。

图3 道路时间序列数据变化谱图

分析图4可以看到，路网中的交叉点(例如交叉点ID为25、54等)连接的路段处于不同交通状态的区域，由于各区域的交通流变化情况并不一致，车辆从某一区域经交叉点进入另一区域时不能很好地同步，使得该交叉点的交通状态不稳定且比较敏感；此外，当某些路段处在相同的同质区域间时(例如路段ID为11、18等)，其全天交通状态的变化情况与周围区域的交通状态并不一致，因此这些路段属于瓶颈路段，产生路段交通流瓶颈的原因可能是由于其附近存在人流量较大的公共场所，如学校、商场及医院等。

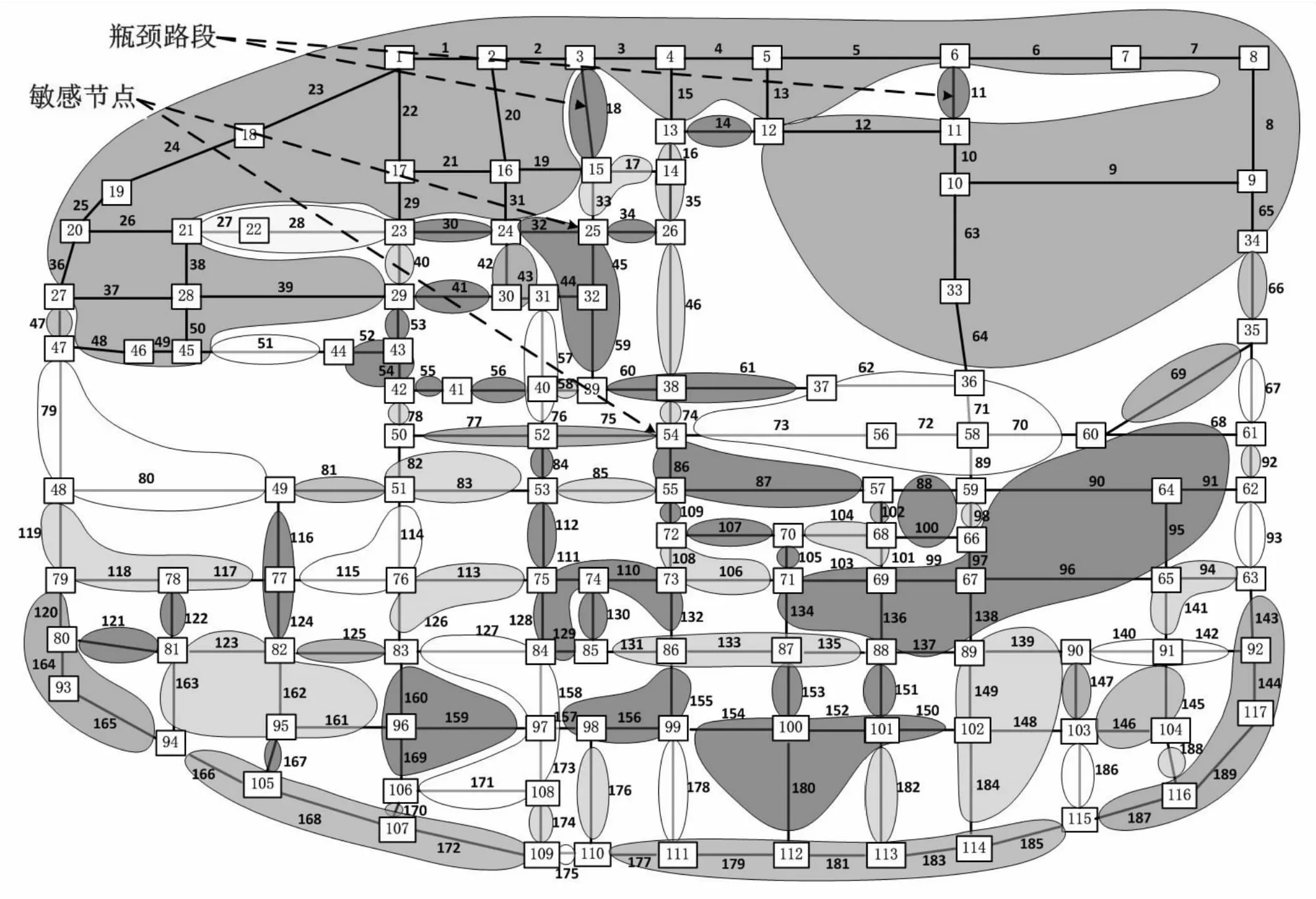
图4 路网同质区域划分

3.3 针对路网同质区域的交通控制策略及诱导

交通网络具有独特的动态特性，应根据聚类结果设计缓解交通拥堵的潜在控制策略[18]。通过对路网时间序列数据的聚类分析，可以识别出路网中的交通状态变化的同质区域，并且还可以挖掘出路网中的瓶颈路段和敏感节点。这里基于同质区域的划分和结论，提出适合的交通拥堵缓解策略：

(1)针对路网中交通状态变化的同质区域，城市交通管理者可以对其进行统一管理，大力发展公共交通，根据路段的拥堵情况，调整人们的出行方式，鼓励人们使用公共交通方式出行，减少私家车的出行，提高公共交通换乘的便捷性[19]，进一步缓解交通拥堵的问题；

(2)针对路网中的瓶颈路段，可以在这些路段设置交通诱导板，并在高峰时段之间完成分流，同时把转移外围剩余车流量作为辅助措施，减少高峰时段车辆临时变道带来的交通拥堵[19]；

(3)针对路网中的敏感节点，可以在这些交叉口设置信号控制对其进行合理的交通流引导，以提高交叉口的通行能力。

4 结束语

依照城市交通路网不同区域内浮动车在不同时段的平均速度来判断某路段的拥堵程度，并对城市路网进行划分，文中提出基于AP算法的城市交通路网划分方法，并将该方法用于路网同质区域划分这一任务中。经过多次实验，证明基于AP算法的交通路网区域划分方法具有很好的稳定性、可靠性和高效性，能够得到有效的交通拥堵区域，同时AP算法可以有效地识别路网中交通状态变化的同质区域，并且能够挖掘出路网中的瓶颈路段和敏感节点，从而可以更好地发现城市交通内部的运行规律，并且为交通管理者制定交通拥堵缓解措施提供有力的理论依据。