阿伏伽德罗常数的新定义对高中化学教学的影响探讨

摘 要：在高中化学教学中，阿伏伽德罗常数属于一个重要的化学计量单位概念。2018年，国际计量大会对阿伏伽德罗常数做出了全新规定。文章对其定义变化的原因做出了分析，并且还对其定义产生的变化给高中化学教学带来的影响做出了深入分析，根据实际情况对教师教学提出建议。

关键词：阿伏伽德罗常数;高中化学;教学调整

中图分类号：G634.8 文献标识码：A 文章编号：2095-624X（2021）39-0039-02

在高中化学教学过程中，以阿伏伽德罗常数为背景的选择题是传统题型之一，属于教学的热点，在试卷上的题型和题量都处于稳定状态，既考查计算关系，又考查对概念的理解进行分析和研究。在此种情况下，教师在教学时还应加强阿伏伽德罗常数的概念性教学，将教学内容进行良好区分，增强教学逻辑性，以此来实现高质量教学。

一、阿伏伽德罗常数

阿伏伽德罗常数主要是借助于X射线的晶体密度来进行测量，主要利用到下列公式：

其中晶胞粒子数量用n表示，硅球半径用r表示，硅球质量用m表示，硅原子量用M表示，晶格常数用a表示。因此，在测定阿伏伽德罗常数的过程当中，需要对单晶硅的原子量、单晶硅球的宏观密度以及晶胞的体积进行测定。 阿伏伽德罗常数属于计量学领域的知识，而计量学属于测量的科学范畴内，从科学和技术内部的某一个领域当中一个不确定度的水平角度，实现对理论和实验方面的相关测量，其中国际单位制属于全球化的统一的计量单位制，属于构成国际计量体系的基础元素。国际计量委员会主要结合了国际纯粹和应用物理联合会、国际纯粹和应用化学联合会以及国际标准化的组织意见，对阿伏伽德罗常数进行了定义。随着现阶段全球化的趋势加快，在多种贸易以及科学发展的基础上，需要运用精准、稳定和普适的单位来进行测量。

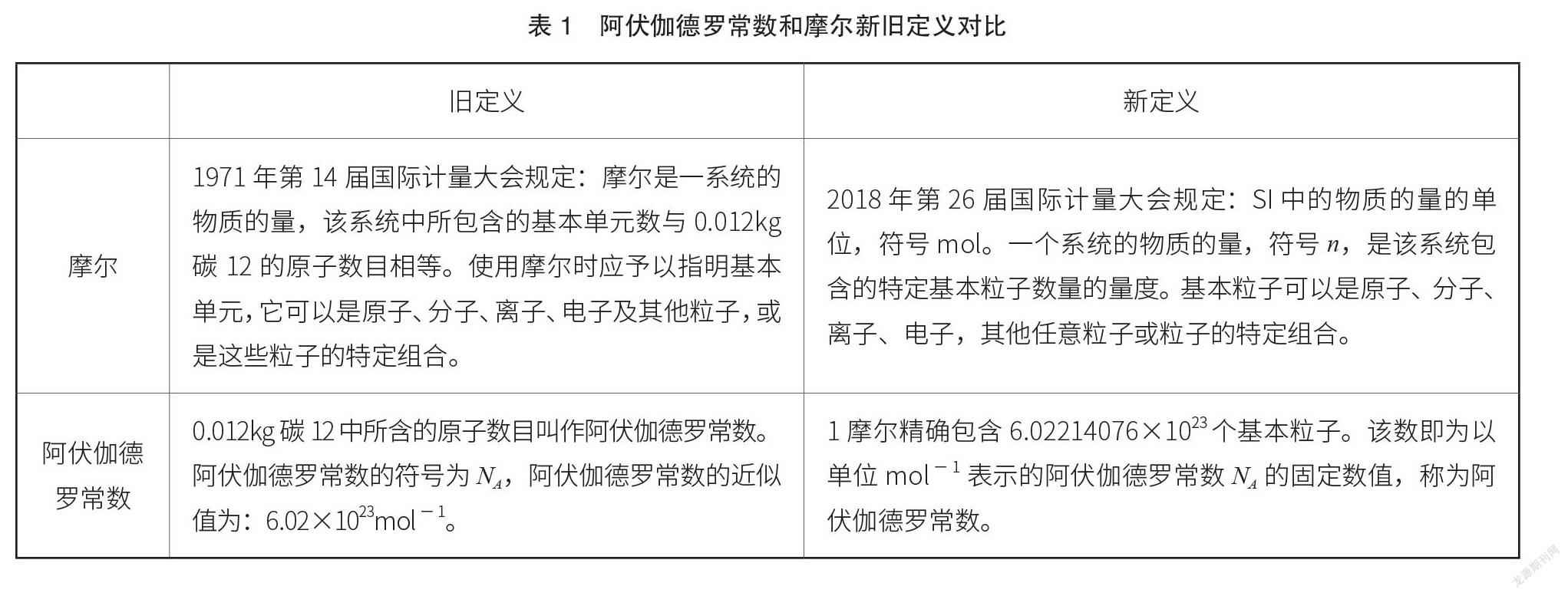
国际单位的制定基本单位主要是基于物理学的理论基础产生的，并基于实物基准和自然的基准进行定义。现代化的计量科学以及技术手段得到飞速发展，传统的计量学逐渐转变为“量子计量学”，基本物理常数的国际单位制的量子化定义也逐渐变得成熟。因此，量子化的定义和实物基准对科学研究、科技生产和科学教育都产生了相当大的影响。将阿伏伽德罗常数和摩尔的新旧定义进行对比分析，可以发现，在1997年的定义当中，摩尔和0.012 kg碳 12 的原子数目是相关联的，在早期的定义当中，“其中最大的问题就是摩尔作为7个SI单位之一，其定义是通过另一个SI单位——千克实现的”，此种方式下的计量对于普适不变的基本物理常数已经全部实现，其基本单位更加稳定、统一。摩尔的新定义直接利用阿伏伽德罗常数（NA）来定义，实现了基本单位定义到物理基本常数当中，此种方式体现了“元测量”的精神，即利用一套稳定的基准来实现测量。在此种方式下的规定可以使得各种物理量不会受制于时间和空间甚至于人工操作而产生的偏差，进行定义和标准的修改。在新定义当中，最大的意义在于可以使得某个特定物质所获得的物质量展现完全一致的效果，如表1所示。

二、定义的修改对高中化学教学的影响

在重新定义之后，摩尔和质量的基本单位不再存在关联，但是在化学测量的工作当中，某种物质当中的待测微粒个数是无法直接测量的，因此化学分析需要先对物质的质量进行称量，借助摩尔质量的公式，对粒子物质的量进行计算。对摩尔进行重新定义之后，需要将物质的质量作为量传溯源的方式，其中对物质的量的计算方法不会改变。

新定义发生的主要变化可以从多个方面分析：其一，对于在1mol的某种微粒集合体当中，所包含的微粒数量和0.012 kg碳 12当中所包含的原子数量是相同的说法，现阶段被定义为大约相同，主要是由于0.012 kg

碳12内部所包含的原子数量不等于6.02214076×1023 个，并且其差距相对较小，对于现阶段的化学分析不会产生过大的精确度影响。其二，对于某种同位素的元素，以前其本身的摩尔质量的数值相对于原子质量来说属于完全一致状态的说法，现在为大约相同，但是其中产生的差距是相当小的，不影响现阶段化学分析的精确程度。其三，阿伏伽德罗常数NA属于一个固定的数值，不再是6.02214076×1023 个基本单元，属于完全等于的状态。其四，对于原先的0.012 kg碳 12包含的原子数等于阿伏伽德罗常数的认知来说，现阶段需要利用固定值来进行阿伏伽德罗常数的代替，也就是6.02214076×1023 。

三、高中化学教学调整

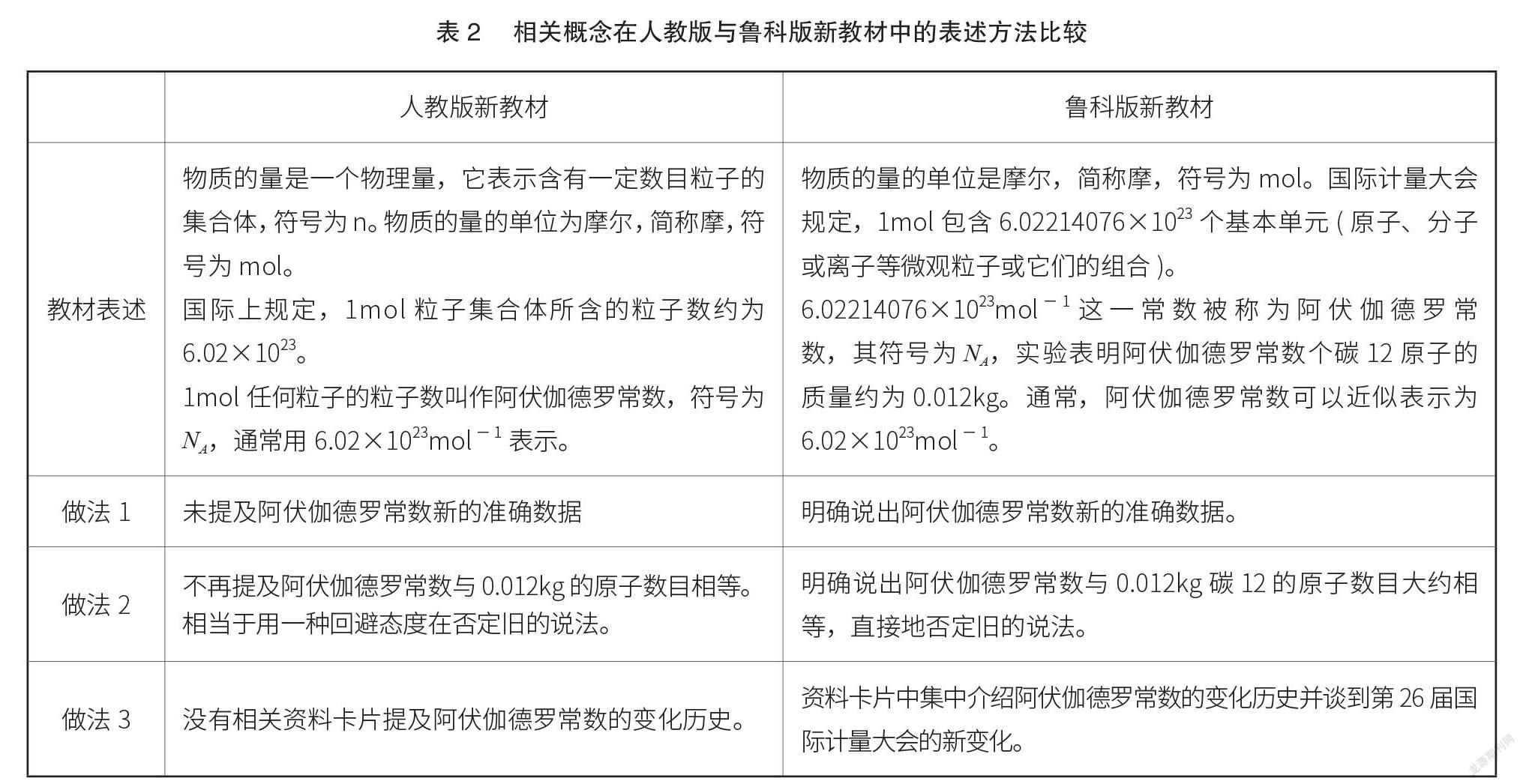
对于相关定义发生的改变，我们可以针对人教版新教材和鲁科版新教材中的表述进行对比，如表2所示。

在教学建议方面，教师需要明确地进行定义说明，因为国际单位制相关内容的宣传和传播需要从中小学的基础教育方面做起。对于和概念相关的判断题，需要进行对应的审核和修订。在规定的摩尔数值当中包含了6.02214076×1023個基本单元，因此摩尔当中包含了对数量的含义。转移的电力数为2mol此种说法虽然具有一定的道理，但是不建议将其直接进行教学，需要利用阿伏伽德罗常数来进行具体个数的换算。

此外，阿伏伽德罗常数属于一个基本的物理常数，其中的主要核心为“宏观辨识与微观探析”。因此，在教学过程当中，教师需要关注概念的科学性和教学的现实性，根据此种理论来进行简单关系的对应和研究，利用不同的模块来获取证据，对不同模块的知识特征进行充分认知。对于元素化合物的教学，教师可以引入实验材料，教学化学反应原理需要进行定量证据的应用，教学物质结构和性质需要进行宏观证据和微观证据的融合，提升学生化学学习的证据意识。除此之外，还要培养学生“证据推理”素养发展的持久性。在高中化学教学当中，证据推理素养不应该局限于具体概念中，学生需要在复杂且真实的问题情境当中进行证据的寻找、分析、推理以及得出结论，在解决问题的过程中巩固学过的知识，学生的高阶思维能力也能够得到锻炼。如此一来，才能使得学生的证据推理素养不会受知识、学科等多方面的限制。

结语

在阿伏伽德罗常数的新定义教学当中，教师要利用辩证的方式来展开教学活动，从全方位、多角度来培养学生的科学思维，锻炼学生的自主学习能力，最终提升高中化学教学质量。

[参考文献]

[1]林建秀.高中化学教学中驱动性问题链设计的实例分析[J].科学咨询（教育科研），2019（5）：71.

[2]郑欣佳，衷明华.浅析高考理综化学选择题解题攻略[J].江西化工，2015（3）：232-233.

[3]祁海娟.攻克高考化学选择题之阿伏伽德罗常数[J].才智，2012（33）：129，24.

[4]黄剑锋.高中化学高效课堂教学模式的研究[J].广西教育学院学报，2012（4）：158-161.

作者简介：陈安航（1986— ），男，广西河池人，中学一级教师，本科，研究方向：高中化学教学。