基于2-阶段成本优化的多播容量供应

杜文龙，黄 余

(1.江苏电子信息职业学院 计算机与通信学院，江苏 淮安 223003；2.圣路易斯大学 研究生院，菲律宾 碧瑶 2600)

0 引 言

网络技术的进步和可用带宽的增长导致了众多媒体内容提供商提供数据传播服务，如实时和按需媒体流。这些媒体内容提供商的一个主要关注点是网络资源(即网络容量)的供应；媒体内容提供商的要求以及对使用资源的付费通过服务级协议(service level agreements，SLA)[1,2]和因特网服务提供商(internet service providers，ISPs)获得。超出SLA中规定限额的使用一般会引起高于SLA中最初商定的额外费用。由于客户的未来需求本身是不确定的，所以媒体内容提供商的初始容量供应过程必须基于预期客户使用模式和需求的预测对成本达成平衡。

由于多播利用了信息的可复制性，从而可获得高效的带宽利用和高吞吐量[3]。如果进一步利用网络编码，将使得多播路由算法是最优的和高效可计算的。对于有向和无向网络中的多播来说，采用网络编码会得到更高的吞吐量以及更便宜的路由成本[3,4]。此外，还可以采用线性规划(linear programs，LP)来计算高效多播。

已有大量文献研究了不同情形下通信网络的容量规划。文献[5]提出了一种用于需求不确定时的容量规划算法；文献[6]针对面临不确定性流量需求时需要提前预留最佳带宽的虚拟专用网络(virtual private networks，VPN)客户，提出了一种基于随机规划模型；文献[7]通过对不同场景下网络资源分配方法进行需求分析，提出了完全垄断和完全竞争的网络资源分配模型；文献[8]提出并分析了一种基于定价的收入管理模型，同时针对随机需求提出了一种基于动态规划的解决方案。

也有不少文献对随机优化进行研究。文献[9]采用随机优化理论对异构网络中的若干关键问题进行了研究，同时介绍了随机优化中采用的一些技术和模型；近年来，随机优化问题还受到了计算机理论界的广泛关注。文献[10]对各种经典组合优化问题的各种随机形式进行了研究；文献[11]将LP四舍五入用来得到随机Steiner树问题的常数因子近似；文献[12]采用了一种新的原始对偶技术来求解随机环境中寻找最优Steiner森林的问题。

资源供应最主要的挑战是未来需求的不确定性，因此，本文假设存在一个概率分布，这个概率分布可以用来估计对多播服务感兴趣的未来客户集，于是将采用网络编码的多播容量供应问题建模为一个2-阶段随机优化问题，目标就是设计指导在第一阶段容量购买决策的算法，从而使得两个阶段的总体成本在预期中最小化。

1 预备知识

将通信网络建模为一个图G=(V,E,C,w)， 其中V是节点的集合，E是边的集合，C和w分别为容量和成本向量。边e∈E有固定容量C(e)， 以及相关的每单位流量成本w(e)。

假设一个固定的源节点s∈V为多播接收者集合T⊂V提供多播服务。要研究的问题是采用网络信息流时，对随机环境中一个给定的数据速率，最优化其多播成本。多播流是一个向量f∈Q+E， 其中Q+是非负有理数集合。假设期望的多播(数据)吞吐量为d，目标是得出一个流量路由方案，使得多播服务的总成本最小化。假设e∈E的每单位流量成本为w(e)， 用W(T) 表示服务集T的多播最优成本，多播成本函数对于有向网络是次可加性的，即对于不相交集合A,B⊆T， 满足

W(A∪B)≤W(A)+W(B)

(1)

网络编码结果表明，当且仅当一个速率d是从源分别到每个接收者的可行单播速率时，d的多播速率就是可行的[13,14]，即如果能在独立单个的会话中得到每个接收者的速率d的单播流，则该速率的多播流也存在。这样，可以把有效多播看作是从源到每个接收者的概念单播流的结合，因而可以通过线性规划来计算概念单播流的有效结合。

假设每个接收者t∈T都有一个通往源的路径集合Pt。对于路径p∈Pt，用f(p)表示沿p从s到t的概念流，用f(e)表示边e上的真实流，则可以通过下面的LP计算最小的多播流成本

Minimize： ∑ew(e)f(e)

(2)

满足

∑p∈Ptf(p)=d∀t

(3)

f(e)≥∑p∈Pt∶e∈pf(p) ∀e,∀t

(4)

C(e)≥f(e) ∀e

(5)

f(e)≥0；f(p)≥0 ∀e,∀p∈Pt,∀t

约束条件式(3)要求全部多播接收者必须获得d的流速率。每个边上的真实流是采用该边的全部概念流的最大值，即

f(e)=maxt∑p∈Pt;e∈pf(p)

(6)

尽管max(·)函数是非线性的，但约束条件式(4)等价地给出了优化方向，最后，每个边上的流量必须遵从容量约束条件式(5)。

图1 不采用网络编码与采用网络编码的成本比较

2 基于2-阶段成本优化的随机多播

2.1 最优多播模型

这部分建立一个随机环境下的最优多播模型。如前所述，本文研究的随机多播问题包括2个阶段。在第一阶段，得到潜在多播接收者集合T的概率分布，这些分布基于市场预测或历史客户使用模式；在第二阶段，将此建模为真实的多播接收者集合A的实现。对于一个接收者t∈T，令P(t) 为t在第二阶段将要订阅的多播服务的概率，并假设这些概率是独立的，即∀t,t′∈T，P({t,t′}⊆A)=P(t)P(t′)。 定义一个膨胀参数λ，它使得在第二阶段中边e的成本从w(e)增加到λw(e)，这相当于使用了超过SLA规定限额而引起的更高价格。目标就是在第一阶段要明智地购买容量，使得在第二阶段中对于多播集的所有可能实现A⊆T的期望总成本最小化。令g∈Q+E为在第一阶段购买容量的向量，hA∈Q+E表示当集合A实现时在第二阶段所需要的额外容量的向量，定义

P(A)=∏t∈AP(t)∏t∉A(1-P(t))

(7)

则可以将2个阶段的最小化期望成本构建为一个LP

Minimize： ∑ew(e)g(e)+∑e∑A⊆TP(A)λw(e)hA(e)

(8)

满足

∑p∈PtfA(p)=d∀t∈A,∀A

(9)

fA(e)≥∑p∈Pt∶e∈pfA(p)∀e,∀t∈A,∀A

(10)

C(e)≥fA(e) ∀e,∀A

(11)

g(e)+hA(e)≥fA(e) ∀e,∀A

(12)

g(e),hA(e),fA(e),fA(p)≥0 ∀e,∀p∈Pt,∀t∈A,∀A

LP式(8)计算服务集A的全部可能实现的最小期望成本即最优解。前3个约束条件表明，对于每个集合A⊆T，网络编码多播的可行性要求必须满足，最后的约束条件表明，在2个阶段购买的容量数量必须足以容纳服务集A的多播流fA。

在独立分布概率的情况下，存在指数级的多个集合A，而且直接用LP式(8)计算最优向量g*是很难的。因此，下面提出2种算法来指导第一阶段的购买，使得总成本接近通过LP式(8)计算得到的最优解成本。

2.2 启发式算法

算法基于以下前提：由于容量因因子λ而变得更昂贵，直观上，如果e上需要c的概率大于1/λ，则可以通过在e上购买容量c来最小化预期成本。

具体来说，假设T是潜在接收者集合，令f为从源到T的全部成员的最优最小成本流。对于每个边e，令ft(e)为该边上从s到一个特定接收者t∈T的总的概念流。由于概念流不竞争带宽，因此，全部接收者在每个边上就存在k≤|T| 个不同级别的总的概念流。用li表示边e上的级别为i∈{1,2,…,k} 的总流量，不失一般性，假设这些级别按总流量的降序排序，即li+1li的接收者t出现的概率，这相当于没有从子集Ti-1(e) 中得到未来接收者的概率。更准确地说，用P≤(li,e) 表示边e需要至多li个单位流的容量的概率，同样，P≥(li,e) 为边e需要至少li个单位流的容量的概率，则P≤(li,e) 可计算为

P≤(li,e)=∏j∈Ti=1(e)(1-P(j))

(13)

此外，还有

P≥(li,e)=1-P≤(li+1,e)

(14)

可见，在预期中，无论概率P≥(li,e) 是否大于1/λ，当单独考虑这个边时，通过购买等于li个单位流量的容量可以使得成本最小化。

将网络中的每个边应用上面的算法思想，其伪代码实现如算法1；算法首先计算最小成本流f，然后检查每个边上不同的概念流级别。然后，算法建议当且仅当P≥(li,e)>1/λ时对于边e购买等于li个流量单位的容量。

算法1： 启发式算法

Input： 潜在多播接受者集合T,t∈T的订阅概率P(t)， 网络图G(V,E,C,w)

Output： 在第一阶段要购买的容量向量g∈Q+E

(1)在T上运行LP式(2), 令f为得到的流;

(2)g(e)∶=0,∀e∈E;

(3)for eache∈Edo

(4) for eacht∈Tdo

(5)ft(e)∶=∑p∈Pt∶e∈pf(p);

(6)F(e)∶={ft(e)|ft(e)>0};

(7) 对F(e)排序, 令l1,…,lk为e上概念流级别的降序;

(8)Ti(e)∶={t|ft(e)≥li} ∀i∈{1,…,k};

(9) for eachi∈{1,…,k} do

(10)P≤(li+1,e)∶=∏j∈Ti(e)(1-P(j));

(11)P≥(li,e)∶=1-P≤(li+1,e);

(12) ifP≥(li,e)>1/λthen

(13)g(e)∶=li;

(14) end

(15) end

(16)end

(17)输出g

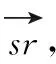
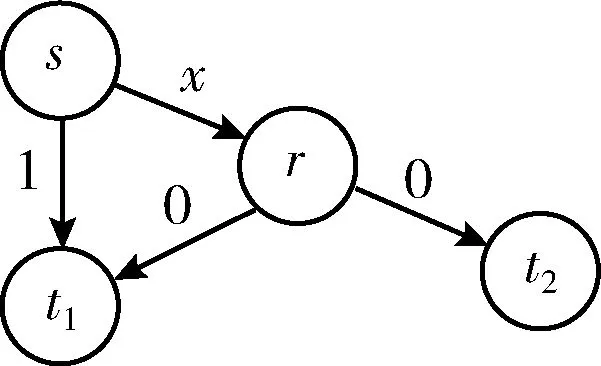
图2 启发式算法导致没有恒定约束的示例网络

在这个示例中算法1性能较差，因为在初始最小成本流计算中没有考虑接收者的概率分布。这就要求求解方法需要考虑初始流计算阶段的分布。因此，下一节提出一种基于采样的方法，为预测未来情形提供一种更准确的方法，并在理论上具有可证明的性能保证。

2.3 采样算法

下面首先给出具体的采样算法，然后证明它的性能约束。

2.3.1 采样算法

算法2： 采样算法

Input： 潜在多播接受者集合T,t∈T的订阅概率P(t)， 网络图G(V,E,C,w)

Output： 在第一阶段要购买的容量向量g∈Q+E

(1)Λ∶={∅};

(3)Ai={∅};

(4) for eacht∈Tdo

(5)r∶=[0,1] 中的随机数;

(6) ifr≤P(t) then

(7)Ai∶=Ai∪{t};

(8) end

(9) end

(10)Λ∶=A∪Ai;

(11)end

(12)在Λ上运行LP式(2), 令f*为最优最小成本流向量;

(13)for eache∈Edo

(14)g(e)=f*(e);

(15)end

(16)输出g

在第二阶段，一旦接收者的真实集合S已知，就需要用服务集合S所需的额外容量来增加第一阶段的解。对于每个边e，用两个边e′和e″替换它。设e′的容量为g(e)，成本w(e′)=0， 并将剩余容量和初始成本分配给e″，即C(e″)=C(e)-g(e) 且w(e″)=w(e)， 则在这个新图上计算得到的最小成本是集合S/Λ对Λ增加的成本，用WAUG(Λ,S/Λ) 表示。

尽管算法本身相对简单明瞭，但关键在于证明算法有一个好的性能约束。为此，首先引入成本分摊方案的概念。成本分摊方案是将多播解的成本分配给接收者集合的一种方法。具体说，给定一个最优多播算法AM，它计算一个接收者集合A的多播成本，则成本分摊方案ξ：2V×V→R≥0将成本份额ξ(A,t) 分配给每个接收者t∈A。

定义1 设AM是一个计算多播最优最小成本的算法，ξ(·,·) 是相关的成本分摊方案，则对于任意两个不相交接收者集合A,B⊆T来说，如果以下3个属性都满足，称ξ(·,·) 为β-严格的成本分摊函数：

(1)ξ(A,t)>0仅当t∈A；

(2)∑t∈Aξ(A,t)≤W(A)；

前两个属性在博弈论中分别称为个体理性和预算平衡[15]。第一个属性表明，如果一个多播接收者没有接收到服务，则不应当要求它支付。第二个属性表明，收到的支付总额不应超过解的成本。最后一个属性关系到集合B中接收者在集合A∪B中被服务时的成本分摊，即将B增加到A的现有解的成本。如果β-严格的成本分摊关于算法AM存在，则B中接收者的成本分摊应该至少涵盖集合A的多播解的增加成本的1/β。β-严格的成本分摊确保了增加的成本可以受到这些成本分摊的约束，因此，改用符号将∑t∈Bξ(A∪B,t) 表示为ξ(A∪B,B)。 下面来表明算法2的性能约束。

定理1 给定一个采用网络编码的多播最优最小成本的相关β-严格的成本分摊函数，算法2构建了一个采用2-阶段随机多播问题的(1+β)-近似解。

由于篇幅所限，这里不给出该定理的证明过程。

注意，算法2未明确采用成本分摊方案。性能约束的证明只需要存在某个β-严格的成本分摊方案，它可以与用于计算最优多播流的算法相关联。因此，本文的目标是证明成本分摊的存在，特别是对于网络编码多播是严格的，并且有有界的严格因子β，这样才能表明算法2是随机多播问题的一个很好的解决方案。对于任意两个不相交集A,B⊆T， 以及一个给定的成本分摊方案β(·,·)， 可以将β定义为

(15)

2.3.2 平均成本分摊是O(|T|)-严格的

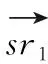
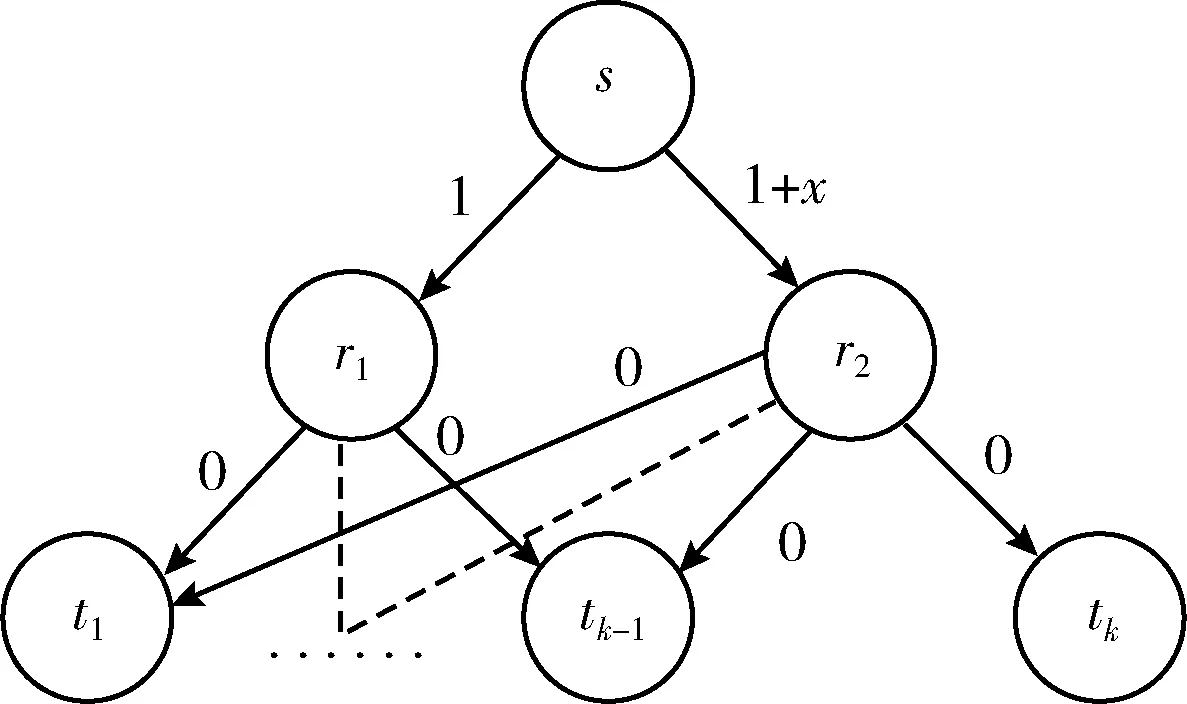
图3 平均成本分摊导致无约束严格因子的网络(这时β=k)

(16)

因此，增加的成本为kξ(T,tk)， 这意味着β=k=O(|T|)。 因此，平均成本分摊对于证明采样算法的约束来说不是一个可行的候选方案。

2.3.3 成本分摊的LP对偶解是2-严格的

LP式(2)的对偶线性规划为下列最大化问题

Maximize： ∑txtd-∑eC(e)s(e)

(17)

满足

∑tyt(e)≤w(e)+s(e) ∀e

(18)

xt≤∑e∈pyt(e) ∀p∈Pt,∀t

(19)

xt<>0；yt(e)≥0；s(e)≥0 ∀t,∀e

在对偶LP中，变量xt、yt(e)和s(e)分别对应于原始LP式(2)中的约束式(3)～式(5)。将对偶最优解表示为 (x*,y*,s*)。 具体来说，如果无限小流量单位是一个非合作多播路由博弈中的自私代理，则基于对偶变量的成本分配方案就能确保最优最小成本流是纳什均衡。因此，对偶解成本分摊方案在非合作网络环境中执行最优多播流。

(20)

因此，变量xt表示t的每单位流量成本，这样，每个接收者的总成本为xtd。但这种成本分配方案只在成本度量w(e)下是预算平衡的，也就是说，如果用成本w(e)+s(e) 替换每个边的成本w(e)，且W′(T) 是该新度量下的最小多播流的成本，则成本分配方案就是预算平衡的，因此∑t∈Txtd=W′(T)。 下面来证明这样的成本分摊方案是2-严格的。

令W(T)为由LP式(2)计算得到的接收者集合T的最优流量成本，考虑下列线性规划

Minimize： ∑ew(e)f(e)

(21)

满足

∑ew(e)f(e)=W(T)

(22)

∑p∈Ptf(p)≥d∀t

(23)

f(e)≥∑p∈Pt∶e∈pf(p) ∀e,∀t

(24)

f(e)≥0；f(p)≥0 ∀e,∀p∈Pt,∀t

在总成本等于W(T)下，LP式(21)使得多播流成本最小化，即目标函数为W(T)。式(21)的对偶LP如下

Minimize： ∑txtd+βW(T)

(25)

满足

xt≤∑e∈pyt(e) ∀p∈Pt,∀t

(26)

∑tyt(e)≤(1-β)w(e) ∀e

(27)

β<>0；xt≥0；yt(e)≥0； ∀t,∀e

下面的引理表明，LP式(25)中的对偶向量x构成了一个有效的成本分摊方案，该方案关于W(T)是预算平衡的。

引理的证明可以直接从LP的对偶性得到。因为两个LP的目标函数有相同的最优解值，因此，具有所述性质的解一定存在。事实上，如果在具有无限边容量的网络中最小成本流更便宜，则对于LP式(25)的每个最优对偶解，可得到β=0。下面给出有效的成本分摊方案。

定义2 令 (x*,y*,β*) 是对于接收者集合T、多播速率为d的LP式(15)的任意最优解，这样β*=0， 则定义成本分摊方案为

(28)

成本分摊方案ξ(·,·) 是一种有效的成本分摊方案，因为它是预算平衡的，而且不在多播集中的接收者有零成本。

下面表明分摊方案ξ(·,·) 是2-严格的，它基于以下3个引理，引理的证明略。

引理2 在网络编码多播中，成本分摊方案ξ(·,·) 对于任意两个不相交集合A和B，ξ(A∪B,A)≤W(A)；

引理3ξ(A∪B,B)≥W(A∪B)-W(A)；

引理4W(A∪B)-W(A)≤WAUG(A,B)≤2(W(A∪B)-W(A))。

由上面3个引理可以得到下面的定理。

定理2 LP式(17)的对偶变量定义了2-严格的成本分摊。

证明：由于成本分摊只适用于多播接收者，因此要尊重个体理性，根据定义，成本分摊也是预算平衡的。根据引理3和引理4得到

(29)

证明完成。

作为成本分摊的对偶变量的严格因子的上界显然是2。现在通过考虑图1所示的网络来给出β的下界。假设目标多播率为1，可以发现对偶变量定义了在这种情形下唯一的成本分摊，例如ξ(T,t1)=1.5， 其中T={t1,t2,t3}。 此外，WAUG(t2∪t3,t1)=2， 因此β=2/1.5=1.333。

定理1和定理2为采样算法提供了理论上的性能保证。

3 算法仿真结果及分析

3.1 仿真环境及设置

仿真在采用C++的BRITE[16]网络拓扑生成器随机生成的网络上进行。BRITE是一种用于生成与Internet非常相似的拓扑工具，它可以用自顶向下和自底向上两种方法来产生GT-ITM层次模型，同时可为多个网络模拟程序提供接口，如NS-2、SSF、Omnet++和Jsim等，并支持可视化工具Otter；BRITE能生成路由器层、AS层以及分层结构拓扑图，并可为连接分配带宽和延迟，具有可视化用户接口；我们在算法中随机分配边容量和成本值，源节点和多播接收者集合也随机选择。除非特别说明，全部接收者都按均匀分布随机分配一个订阅概率。在第一阶段，根据算法1和算法2的建议购买容量，在第二阶段，用接收者的订阅概率随机生成真实的接收者集合，并以膨胀因子为λ的价格购买额外的容量。得到的每个数据点是重复实验200次并取平均值的结果；为了表明本文算法的性能，将通过LP式(8)得到的最优解作为比较基准，并与文献[8]的基于网络收益最大化的定价管理模型的成本解进行比较。

3.2 仿真实验结果

图4为对于不同网络大小和不同多播接收者数量得到的不同算法的解成本，其中膨胀参数λ设置为5。可见，对于不同网络大小时，本文提出的两种算法与最优解非常接近，甚至在某些情形下还优于最优解。对于不同多播接收者数量时(这时网络大小固定在100个节点)，启发式算法始终优于最优解；还可看到，在两种情形下，启发式算法略优于采样算法，而且在两种情形下，本文的两种算法始终优于文献[8]的方案。

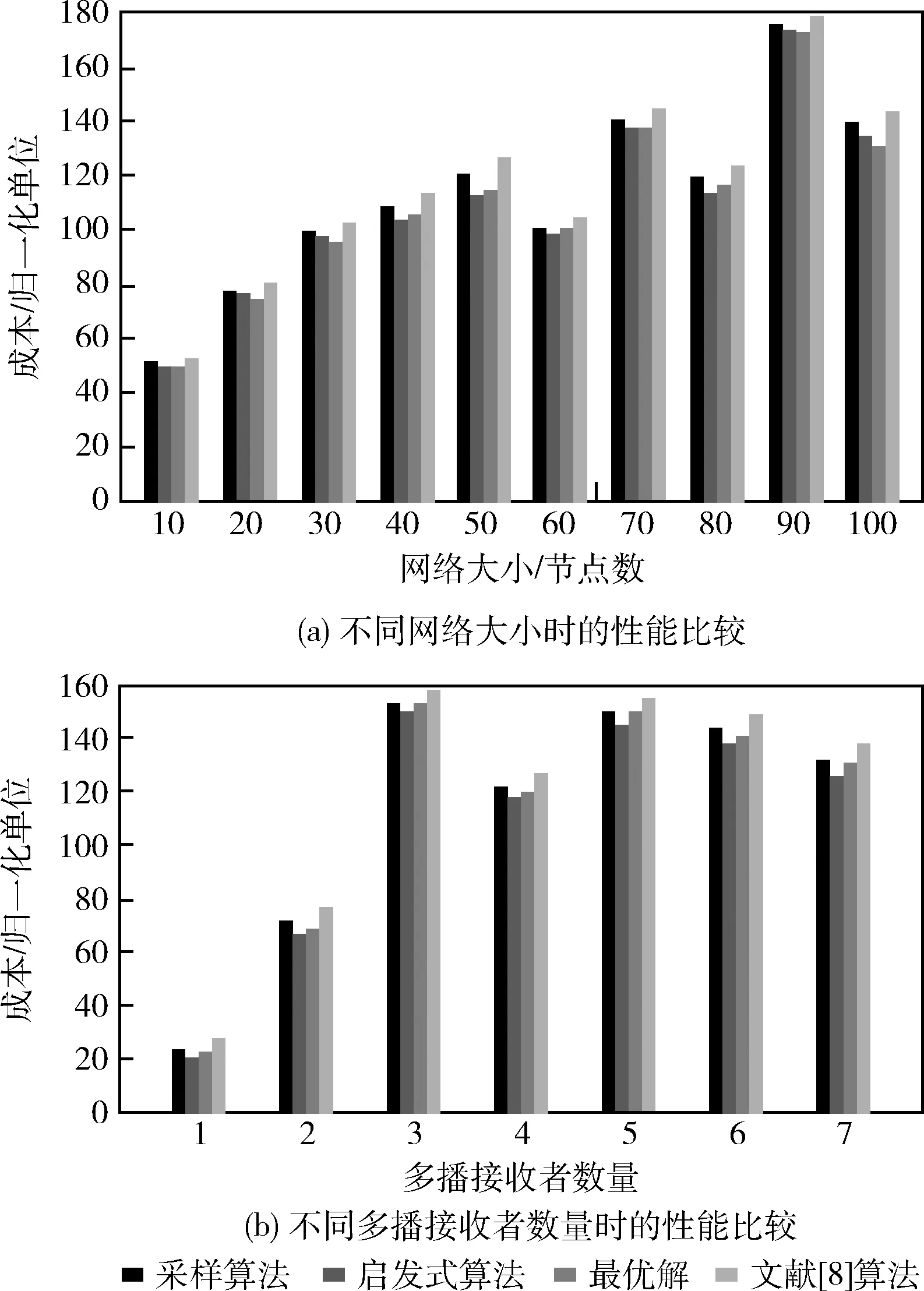
图4 不同算法得到的解成本比较

图5为膨胀参数λ对两种算法性能的影响。对于小的λ值变化，如图5(a)所示，两种算法的性能与最优解的差都在10%以内，基本不受λ值的影响；随着膨胀参数的不断增大，如图5(b)所示，两种算法的性能基本都能收敛到最优解。这是因为当第二阶段的成本增大时，两种算法都能为第一阶段的全部接收者集合提供最优解。

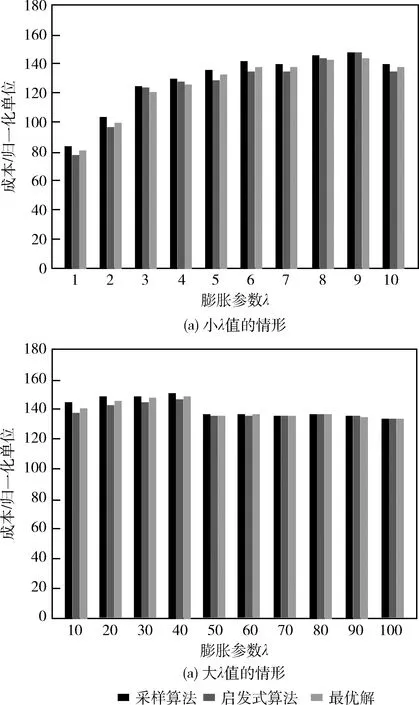
图5 膨胀参数λ对算法1和算法2性能的影响

由前面分析知道，启发式算法在初始最小成本流计算中不考虑接收者的概率分布，从而在某些情形下可能运行很差，而采样算法考虑了接收者的概率分布，为预测未来情形提供了一种更准确的方法，并具有理论上的性能保证。为了比较两种算法，我们将订阅概率在范围[0,0.1]内均匀抽取，网络大小由100个节点构成，有10个多播接收者且设置λ=10；图6为通过启发式算法和采样算法得到的解成本。可以看到，两种算法的解都接近最优解，但采样算法的性能要优于启发式算法。原因是启发式算法最初计算全部接收者的最优多播流，可能最终在更昂贵的边上购买容量，另一方面，当在计算第一阶段的目标多播集时，采样算法通过考虑订阅概率来求解这个问题；还可看到，随着极低订阅概率的接收者数量的增加，与采样算法相比，启发式算法的性能受到的影响越来越大。

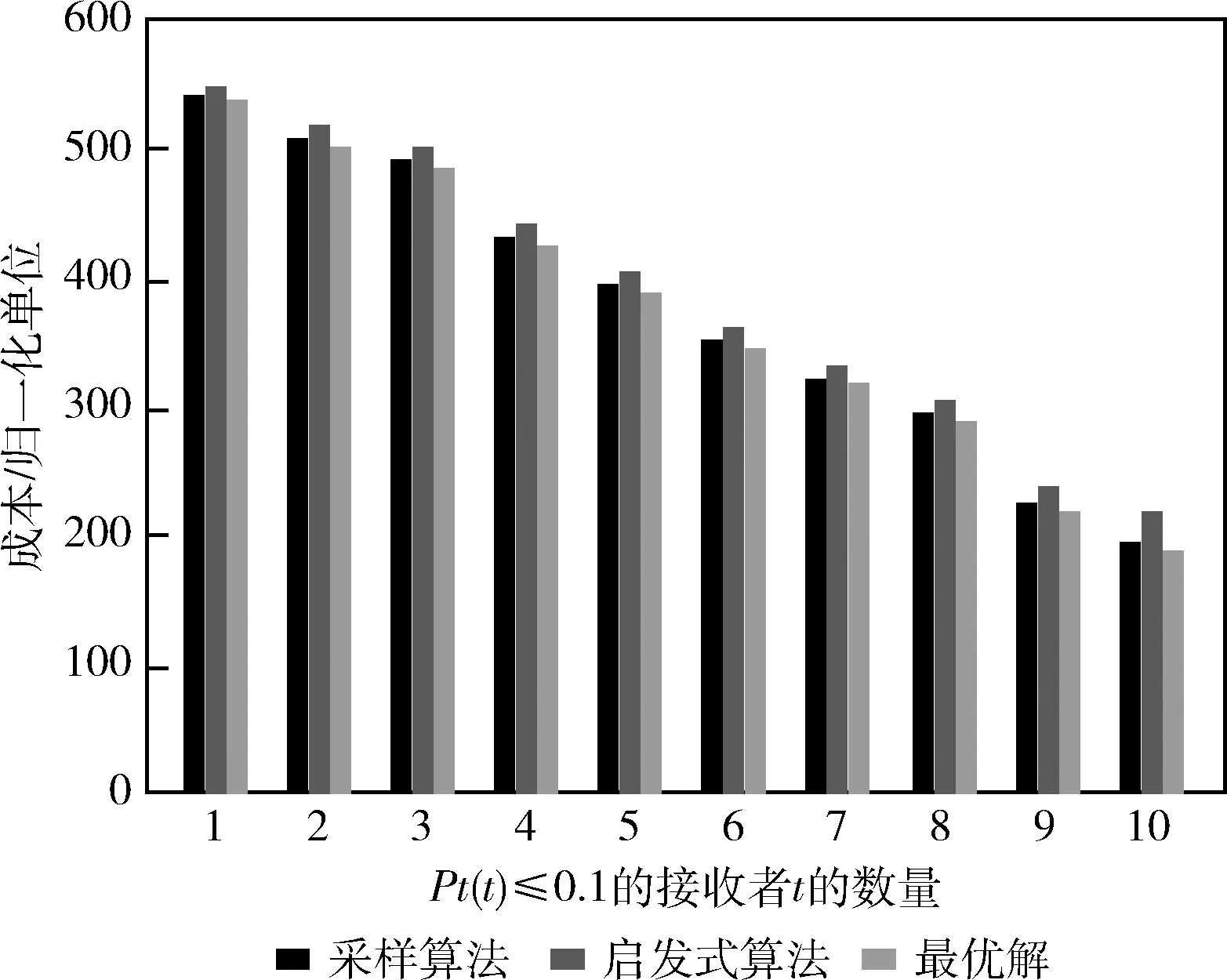
图6 不同订阅概率接受者数量对算法性能的影响

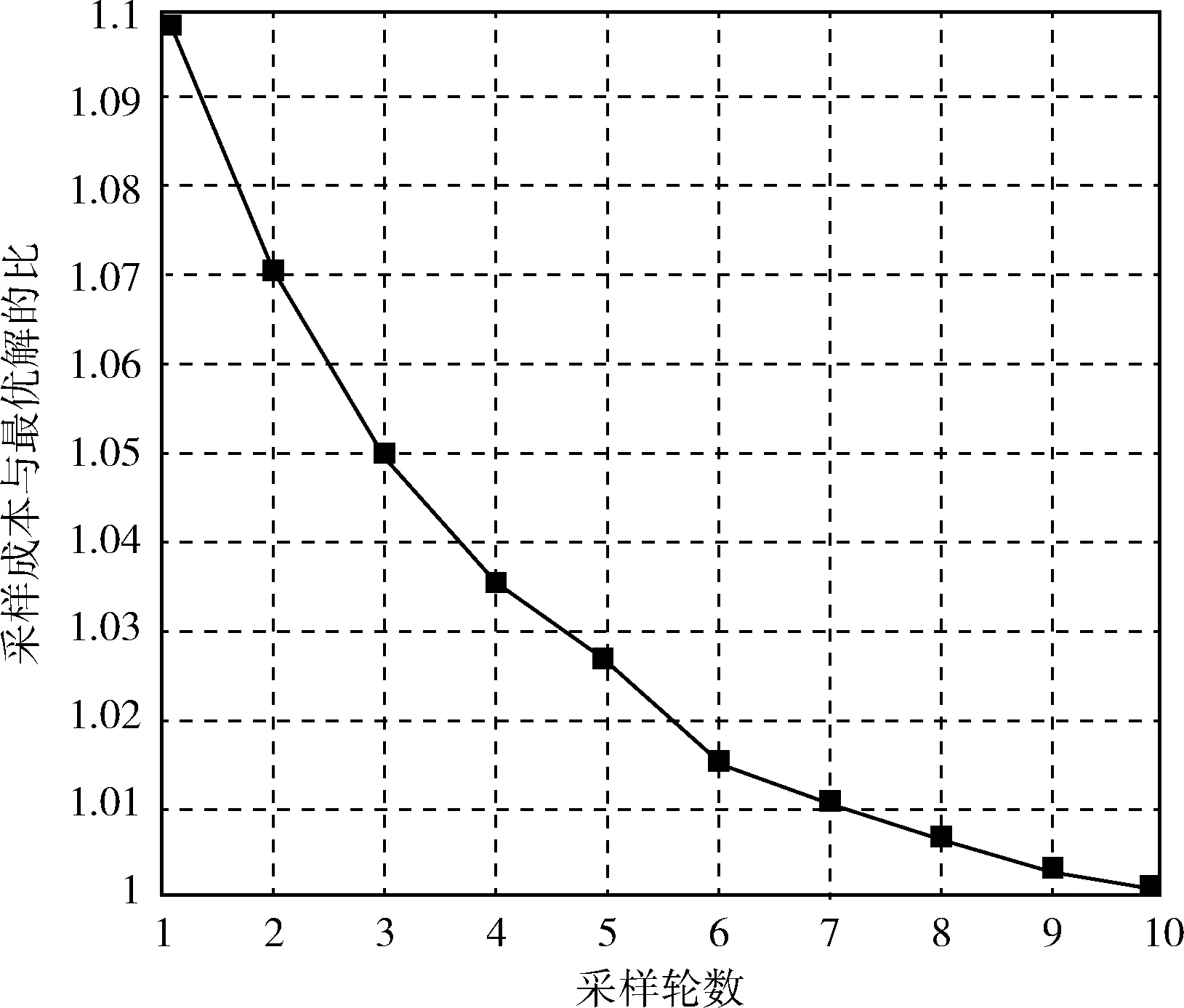
图7 采样轮数对采样算法性能的影响

4 结束语

由于互联网数据传播服务的普及以及内容提供商和ISPs之间的SLA商业模式，明智的多播容量规划使得其自身成为一个重要的研究方向；本文将具有不确定性的多播容量规划构建为一个具有追加的2-阶段随机优化，提出了2种解决方案，即利用网络编码优势的启发式解决方案和进一步结合采样技术的改进方案。仿真结果表明，2种解决方案的实际性能接近最优解的性能。

尽管本文的研究为采用网络编码的多播容量规划问题提供了新的见解，但仍存在一些局限性。本文的解决方案更适用于替代网络，如无线Mesh网或大规模无线Ad-hoc网络，所以将本文的研究扩展到更好的内容分发模型系统是未来研究的一个重要方向；此外，本文的研究只考虑了在所有网络链路的成本一致增加的情况，且只有一个不确定的阶段，还存在非均匀的成本增加，以及多播接收者可以动态订阅和离开多播会话的多个阶段，这些都是我们未来研究的内容。