空水两栖子母系统设计与研究

马跃，李洁，唐雪，蒋海洋，王叶文

(西南科技大学四川省特殊环境机器人技术重点实验室，四川绵阳，621000）

0 引言

进入21世纪之后海洋问题日益显得突出，领土争端、资源勘探、海洋污染、温室效应等问题已经成为困扰人们的热点问题，迫切需要具有在复杂环境搜寻功能的机器人系统。相比于单种机器人平台，两栖机器人具有灵活性高、适应性强、多功能运动模式等技术优势，在目前机器人作业环境日益多元化和复杂化的情况下具有广阔的应用前景。

目前国内外两栖机器人的研究多采用变换推进方式实现水空工作模式切换，但大多机器人结构复杂，对于工作环境要求较高。一款由哈尔滨工业大学[1]设计的动璞明轮式两栖机器人，采用在橡胶轮胎内侧加上璞板的方式让机器人在水中也具有前进能力。该机器人结构设计简单，具有很强的实用性，但因其两个运动方式同时进行，动力浪费严重，续航能力不足。哈佛大学在2015年设计研发了一款水空两栖仿昆虫机器人Robobee[2]，采用扑翼方式提供在水空流体中航行的动力，在水中和空中都具有较好的俯仰控制[3]，并具有较好的自主航行能力。但该机器人系统的供电系统具有较大的问题，不能长时间的处于工作状态。

基于以上研究和问题，我们探索出一套空水结构与子母协作的机器人系统，具有环境适应能力强、灵活性高、工作时间长等优势特点，可解决当前单种机器人在水、陆、空三域搜寻定位的灵活性差、适应性弱和多功能运动模式受限等问题，为国家公共安全的监测、预警与应急处理提供应用理论和技术储备[4]。

1 系统设计

空水两栖子母系统的设计分为子体系统和母体系统两部分。母机器人采用水上浮球轮式机器人，主要实现水上和陆地运动，可提供大容量电源，为子机器人的续航时间提供了保障。由车舱、浮轮、主控装置、推进装置、释放装置、气涨装置、传感器装置、定位及通信装置等部分构成。

子体系统为水空可变结构飞行器，主体为呈圆盘形的多自由度两栖飞行器，用于满足低空及浅域的探测，采用空中固定旋翼式螺旋桨加水中涵道式螺旋桨形式推进。系统硬件包括控制器、空中与水下动力系统、视觉系统、姿态测量系统、通信系统、电源系统等模块。

子系统与母系统配合，组成一个工作环境适应性强、活动范围大、便于使用等诸多优势的空水两栖子母搜寻定位系统。

2 运动控制器设计及仿真

2.1 机械结构设计

空水两栖机器人的机械结构设计主要包括机身、涵道推进器及旋翼装置三部分。其机身由机身底座和机身顶盖通过螺钉紧固连接，并构成一完整的碟形机身[5]；其涵道推进器设置于机身外围，对称安装于机身左右两端面，并通过舵机臂与机身内部的防水舵机相连；机身表面开设六大通孔作为旋翼装置的旋翼域，且分别穿过通孔中心设置径向机轴，径向机轴中部开设电机槽，电机槽内部安装防水无刷电机，螺旋桨即安装于防水无刷电机上方[6]。其机械结构示意图如图1所示。

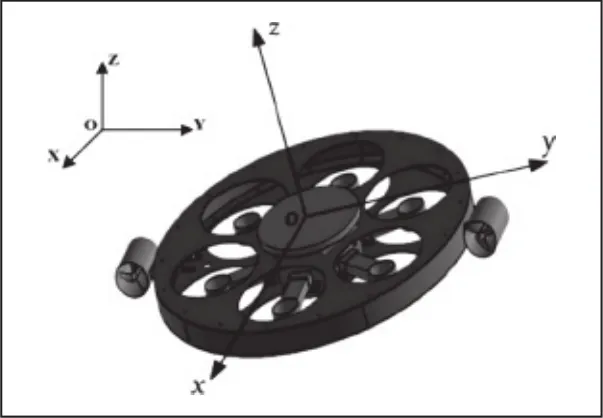
图1 空水两栖机器人机械结构示意图

2.2 运动学及动力学模型

空水两栖机器人在空中和水下的运动过程中，会受到很多因素的影响，为了便于建立空水两栖机器人的运动数理模型[7]，做出如下假设:

（1）空水两栖机器人为刚体，不易形变；

（2）空水两栖机器人的重心与机体坐标系原点相重合；

（3）空水两栖机器人呈完全均匀对称。

由欧拉角定义，机体坐标系和地面坐标系原点重合，地面坐标系可经过三次旋转得到机体坐标系[8]，设飞行器相对地面坐标系旋转的欧拉角为横滚角φ、俯仰角θ和偏航角ψ。

首先，绕Z轴旋转ψ，X转到X'，Y转到Y'，对应的旋转矩阵为RZ,ψ。其次，绕Y'轴旋转θ，X'转到X''，Z转到Z'，对应的旋转矩阵为RY,θ。最后，绕X''轴旋转φ，Y'转到Y''，Z'转到Z''，对应的旋转矩阵为RX,φ。

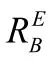
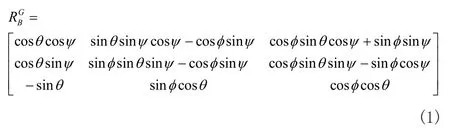
则当机体坐标系下各位置量已知时，则可根据上述规则，将其转换到大地坐标系下：

将上式等式两边的位置量对时间求导，可得线速度的转换关系。同时，根据欧拉角定义横滚角φ、俯仰角θ和偏航角ψ，进行微分几何推导可得到角速度的转换关系：

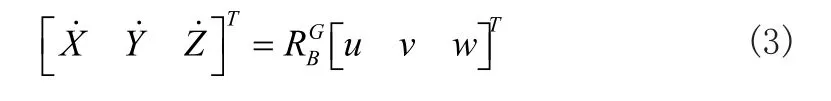
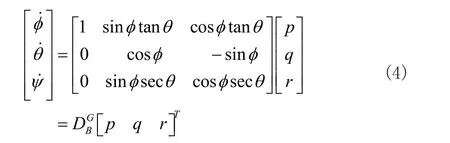
式中u、v、w分别表示机体沿X、Y、Z轴平动时的线速度，p、q、r分别表示机体围绕X、Y、Z轴转动时的角速度。将式（3）和式（4）联立可得到空水两栖机器人的运动学方程，如式（5）所示 ：

空水两栖机器人的运动可以简化为平动和转动，平动方程满足牛顿第二运动定律，转动方程满足欧拉定理。六自由度机器人动力学方程可如下式所表达：

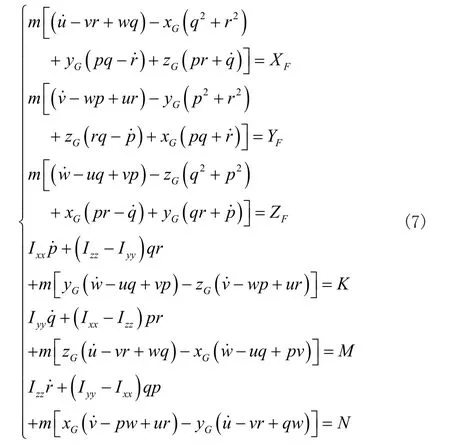
2.3 控制器设计

本系统的控制器设计目标是实现对空水两栖机器人的位置和姿态进行控制，而运行环境的不确定性以及存在的外界干扰等都会增加控制的复杂度。所以控设计采用了经典的PID控制模型[9]，在被控对象的模型有较多不确定性因素和外界干扰环境干扰的情况下，同样适应性强，鲁棒性好。控制器使用串级PID控制的方法，将空水两栖机器人的控制算法分成两个回路，构成外环位置控制回路和内环姿态控制回路，空水两栖机器人控制模型框图如图2所示。

图2 控制器设计框图

控制器的被控对象为机体位置坐标，初始输入为预设位置坐标，输出目前位置坐标，两坐标的偏差值作为反馈信号，使得对机体方向和姿态进行控制完成当前位置的修正。

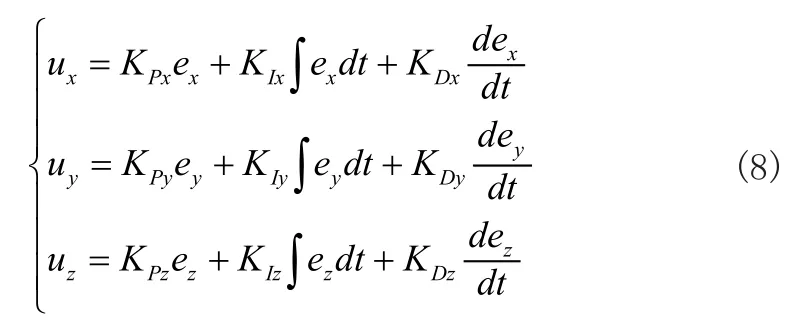
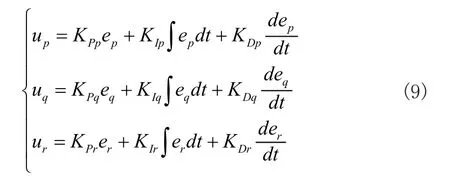
2.4 控制器仿真

为了验证理论上控制器的相应性能，在MATLAB里建立了相应的仿真模型并对其进行了相应的仿真验证[10]，系统位置及姿态仿真结果如图3所示，可知控制系统稳态误差基本为零，同时系统反应速度较快，控制器控制机体x、y、z方向上的位置与姿态，从初始状态到达预设位置经过10s～20s即可到达稳定。

图3 空水两栖机器人xyz方向位置及姿态仿真曲线图

3 结束语

本文设计了一套水空结构与子母协作的机器人系统，分别进行了母体和子体的机械结构设计和软硬件系统设计，并且进行了空水两栖机器人运动模型建立和控制器的设计与分析[11]，最后结合仿真结果对整个控制器的运动控制性能进行了验证。解决了当前单种机器人在水、陆、空三域搜寻定位的灵活性差、适应性弱和多功能运动模式受限等问题，为国家公共安全的监测、预警与应急处理提供应用理论和技术储备。