基于迭代函数系统的三维树木静动态可视化研究

胡杰　刘娟　邓林强　李富忠

摘要：基于树木实测数据，转化为迭代函数系统的IFS码，用Matlab软件分别实现合轴分枝树木和单轴分枝树木三维静动态可视化模拟系统，用于城市和园林等的规划与设计。以槐树和松树分别作为合轴分枝树木和单轴分枝树木的代表，提取树高、分枝数、分枝仰角、方位角、枝长等重要信息进行数据统计分析;将父枝（一级枝）和子枝（二级枝）的枝长粗细比、方位角、仰角等参数进行分析推导，得到迭代函数系统的IFS码，并计算出每个仿射变换相应的概率;最后再用Matlab软件进行编程，对其形态进行三维可视化静动态模拟。试验过程中，通过调整并改变树木的IFS码及相应的概率，可以对树木进行旋转、平移和缩放变换，并且呈现树木的多种形态（枯萎、修剪等）。研究的函数迭代系统方法在虚拟自然景观（山川、植物、云等）方面具有很广的应用，并且程序简单，仅通过对应的IFS码和对应的概率，即可在三维空间中再现不同自然景观的静动态。

关键词：静动态可视化;迭代函数系统;三维树木;IFS码;合轴分枝树木;单轴分枝树木

中图分类号：S126 文献标志码： A文章编号：1002-1302（2021）19-0205-04

树木形态各异，种类繁多。按照分枝模式分为如下两大类：（1）单轴分枝树木，有明显粗壮而直立的主干，顶芽一直向上生长，树形挺拔，形态简单，如杨树、松树、银杏等^[1-2]。（2）合轴分枝树木，无明显主干，树冠呈开展状，顶芽发育一段时间后停滞或死亡，被下面的侧芽取代，有多个弯曲的主轴，形态相对复杂，如枫树、桃树、柳树、槐树等^[3-8]。

综上，树木的形态结构很难用传统的几何法来模拟。但是考虑到树木整体和局部的自相似性，故引入分形几何学^[9]。常见的分形方法有L系统法、粒子系统法、迭代系统法^[1-13]。L系统法的生成规则是由字符串体现的，对于复杂的树木形态，字符串难以获得和使用;粒子系统法缺乏真实感，有明显的人工痕迹，无法细致地刻画光照和树木纹理;迭代函数系统法克服了上述2种方法的缺陷，程序简单，仅需几组仿射变换的系数（IFS码）和相应的概率，便可细致刻画树木的纹理结构，描绘出形态逼真的不同树木。

近年来，树木可视化研究的课题引起了大量学者的关注。 Sievanen等利用Matlab软件，基于分形L系统，对白杨树进行二维可视化研究^[1]。吴欠等利用C语言，基于迭代函数系统实现了杉木三维静态可视化研究^[2]。赵庆丹等利用C语言，基于迭代函数系统实现了红松三维静态可视化研究^[8]。但是上述文献都没有引入随机因子，描述出的树木形态比较呆板，不自然。Prusinkiewicz引入随机因子，利用Matlab软件，分别基于L系统和迭代系统，形象地模拟不同树木的形态^[6]。朱华等基于迭代函数系统，利用C语言模拟动态树木^[10]。相关研究均为二维图形，只是从某一侧面反映树木的平面图形，无法真实地刻画树木的整个图形，故亟需将树木的二维图形推广为三维图形^[1，6，10]。

Matlab软件程序简明，语言简单，在处理图形图像方面很有优势。但是对于树木可视化研究而言，用Matlab编程的比较少。在此基础上，本研究将利用Matlab软件，基于迭代函数系统，分别以槐树、松树作为合轴分枝树木、单轴分枝树木的代表，通过对树木数据进行分析统计，得到IFS码和相应的概率，分别实现合轴和单轴分枝树木的三维静动态可视化研究。

1合轴分枝树木数学建模

1.1数据统计分析

合轴分枝树木形态相对复杂，故先对其进行研究，以槐树为例。槐树为我国古老的树种，分布广泛，有着悠久的历史，受人们喜爱和崇拜;尤其是山西洪洞大槐树，已经成为著名的旅游景点。

本研究选取3株冠形比较好的槐树样木进行数据统计分析，分别提取树高、分枝数、父枝（一级枝）和子枝（二级枝）的仰角、主干长、胸径、冠幅等重要信息（表1）。

统计选定的槐树的一级枝和二级枝的方位角、仰角、枝长和枝径的分布范围，并求其平均值、标准差、最大值、最小值。如表2所示，一级枝（父枝）枝径的平均值大于二级枝（子枝）枝径，一级枝枝长和仰角的平均值小于二级枝枝长和仰角。

1.2提取槐树的IFS码

基于迭代函数系统模拟槐树三维图形，借助Matlab编程，程序简单，仅需确定仿射变换的系数（IFS码）。仿射变换种类很多，为了确保树木图形不失真必须为压缩变换。描绘三维树木图形一般需要12个系数，可以通过3个方程组求解得到。具体方法如下：在原图中找4个点A（x₁，y₁，z₁）、B（x₂，y₂，z₂）、C（x₃，y₃，z₃）、D（x₄，y₄，z₄），在仿射變换后的子图中找到对应的4个点A′（x₁′，y₁′，z₁′）、B′（x₂′，y₂′，z₂′）、C′（x₃′，y₃′，z₃′）、D′（x₄′，y₄′，z₄′）即可建立下列3个方程组：

ax₁+by₁+cz₁+u=x₁′

ax₂+by₂+cz₂+u=x₂′

ax₃+by₃+cz₃+u=x₃′

ax₄+by₄+cz₄+u=x₄′;（1）

dx₁+ey₁+fz₁+v=y₁′

dx₂+ey₂+fz₂+v=y₂′

dx₃+ey₃+fz₃+v=y₃′

dx₄+ey₄+fz₄+v=y₄′;（2）

gx₁+hy₁+kz₁+r=z₁′

gx₂+hy₂+kz₂+r=z₂′

gx₃+hy₃+kz₃+r=z₃′

gx₄+hy₄+kz₄+r=z₄′。（3）

但是这样得到的IFS码不准确，所绘图形比较失真，并且在三维中点的寻找比较困难。故三维中描绘图形一般不采用上述方法。仔细分析上述3个方程进行对应的仿射变换，可以将其进行简化：

式中，矩阵C为枝长比，即一级枝与二级枝的长度粗细比例;α为二级枝的方位角，即绕y轴旋转α角;β为二级枝的仰角，即绕z轴旋转β角;B矩阵为平移变换，代表枝长。

根据调查统计的槐树基本数据（表1、表2），找到相应的参数，带入公式（6）中，得到迭代函数系统中槐树的IFS码（表3），即参数a、b、c、d、e、f、g、h、k、u、v、r。当i=1，2时，对应的仿射变换描绘的就是槐树的主干，当i=3，4，5时，仿射变换描绘的是槐树的枝干;槐树分枝的个数用迭代次数来确定，槐树分枝的位置和大小分别用父枝和子枝各自的仰角、方位角和枝长比来确定。

然后计算每个仿射变换对应的概率（P_i）。概率表示的是子图的体积或面积在原图中所占的比例，利用向量的混合积可以表示体积，转化为矩阵^[6]，所有的概率之和必須为1：

式中：N表示描述图形所需的IFS码的组数;ai，bi，…，ki表示第i组IFS码。

把表3中每组参数依次分别带入式（7）中，经过简单的计算，得到仿射变换的概率依次为0.25、0.15、 0.13、0.12、0.35。利用Matlab软件编程，得到槐树的图形，如图1所示。

1.3呈现槐树的不同状态

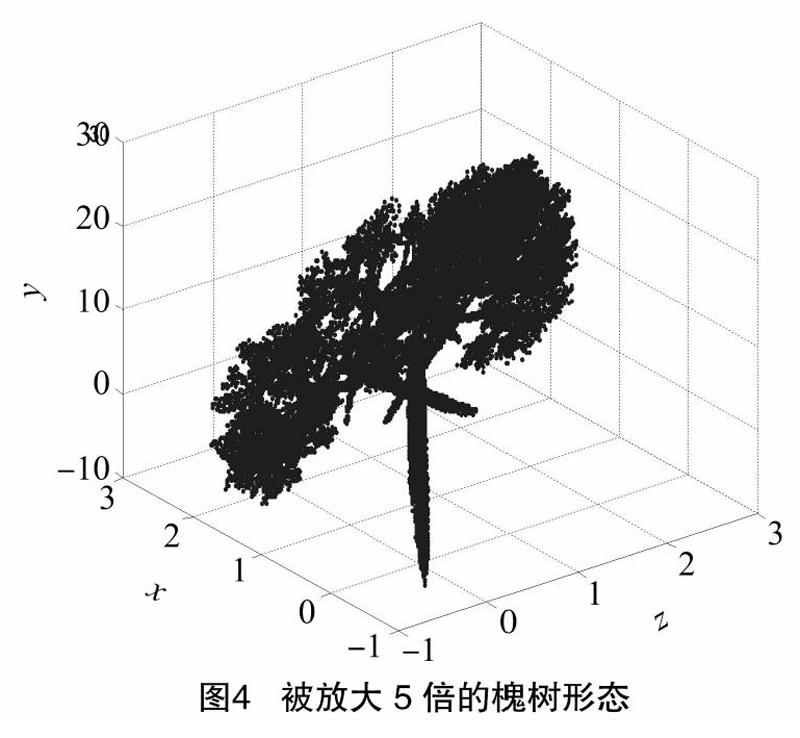
通过以下2种方式可呈现槐树的不同状态：（1）改变槐树仿射变换的概率，调节各仿射变换的强弱，如将对应的概率依次改为0.36、0.34、0.09、011、0.10，此时描绘的是冬天无叶枯萎的槐树（图2）;同理将概率依次改为0.06、0.14、0.37、0、043，即去掉i=4时的仿射变换，此时描绘的是树枝被截断的槐树（图3）。还可以通过提高相应的概率使树木枝叶向阳的地方变得更加稠密，调整相应的概率改变主枝干的粗细等。（2）通过将系数矩阵A乘以特殊矩阵，改变槐树的IFS码。如乘以缩放矩阵

2单轴分枝树木数学建模单轴分枝树木形态相对简单，以松树为例。松树在我国北方随处可见，树型特别笔直，四季常青。笔者用同样的方法，选取3株冠形比较好的松树样木进行数据统计，提取树高、分枝数、分枝仰角、方位角、枝长等重要信息以及相应的范围，得到一级枝枝径和仰角的平均值大于二级枝枝径和仰角，一级枝枝长的平均值小于二级枝枝长。用同样的方法得到迭代函数系统中松树的IFS码（表4）并计算

出相对应的概率，依次为0.01、 0.70、0.09、0.04、006、0.03、0.07。利用Matlab软件编程，得到松树的图形（图6）。同样地，可以通过调整松树仿射变换对应的概率和对仿射变换的系数A乘以一些特殊矩阵改变相应的IFS码，从而呈现松树的不同静动态。

本研究分别以槐树、松树作为合轴分枝树木、单轴分枝树木的代表，提取树高、分枝数、分枝仰角、方位角、枝长等重要信息，进行数据统计分析。将一级枝和二级枝的枝长粗细比sx、 sy、 sz，方位角α和仰角β参数，代入公式（6）中，得到迭代函数系统的IFS码，用Matlab软件进行编程。通过调整仿射变换对应的概率和对仿射变换的系数A乘以一些特殊矩阵改变相应的IFS码，呈现树木的不同状态效果，从而实现三维树木的静动态可视化研究。

此方法通过具体的例子给出如何通过树木的实测数据得到相应的IFS码，有着广泛的应用前景。实际操作中只需要调整Matlab程序中IFS码就可以模拟不同树木、植物、山川、云等自然景观的静动态，程序简单，易于操作。此虚拟树木技术可以应用于很多地方，其中包括数字电影、动画、城市和园林等的规划和设计以及具有场景模拟的类似领域。

参考文献：

[1]Sievanen R，Nikinmaa E，Nygren P，et al. Components of functional structural tree models[J]. Annals of Forest Science，2000，57（5/6）：399-412.

[2]吴欠，张怀清，陈永富，等. 杉木形态三维可视化模拟技术研究[J]. 林业科学，2010，23（1）：59-64.

[3]刘娟，胡杰，张权义，等. 基于随机分形的树木（枫树）可视化研究[J]. 山东农业大学学报（自然科学版），2020，51（3）：495-499.

[4]胡秀珍，张建，李淼，等. 基于参数L系统的梨树枝干模型三维可视化[J]. 计算机系统应用，2011，20（8）：86-90.

[5]Allen M T，Prusinkiewicz P，Dejong T M. Using L-systems for modeling source-sink interactions，architecture and physiology of growing trees：the L-PEACH model[J]. New Phytologist，2005，166（3）：869-880.

[6]Prusinkiewicz P. Modeling plant growth and development[J]. Current Opinion in Plant Biology，2004，7（1）：79-83.

[7]吴翔，高晓阳，邵世禄，等. 基于参数L系统的葡萄果枝生长可视化研究[J]. 中国农机化学报，2017，38（5）：63-68.

[8]赵庆丹，罗传文，孙海洪，等. 基于OpenGL和VC的樹木三维可视化模拟实现[J]. 东北林业大学学报，2010，38（11）：54-57.

[9]高扬，黎展荣，魏为，等. 基于参数L系统的小叶榕树建模方法研究[J]. 计算机技术与发展，2016，26（7）：156-159.

[10]朱华，姬翠翠. 分形理论及其应用[M]. 北京：科学出版社，2011：54-79.

[11]邹运兰，杨志红，王仁芳. 基于迭代函数系统IFS的动态树木模拟[J]. 计算机应用与软件，2012，29（3）：118-121.

[12]李佳祺. 基于中性景观模型的虚拟森林场景的构建方法研究[D]. 南京：南京大学，2018：11-20.

[13]Pradal C，Boudon F，Nouguier C，et al. PlantGL：a Python-based geometric library for 3D plant modelling at different scales[J]. Graphical Models，2009，71：1-21.

基金项目：山西农业大学科技创新基金 （编号：2017005、2017019）。

作者简介：胡杰（1986—），男，山西吕梁人，硕士，讲师，主要从事图像处理和大数据相关研究。 E-mail：17835425155@163.com。

通信作者：刘娟，硕士，讲师，主要从事应用数学和生物数学研究。 E-mail：liujuannk@163.com。