基于IR-UWB 雷达的非接触式呼吸检测方法

党小超，张金龙，郝占军，安 莹

（1.西北师范大学 计算机科学与工程学院，兰州 730070；2.甘肃省物联网工程研究中心，兰州 730070）

0 概述

自2002 年美国联邦通信委员会（Federal Communications Commission，FCC）批准民用微波的频率范围为3.1～10.6 GHz［1］以来，超宽带（Ultra Wide Band，UWB）因具有低功耗、强穿透能力、强抗干扰能力、高分辨率等特性，被广泛用于地震灾害救援、室内定位［2-3］、穿墙检测等任务中。雷达可以通过感知由呼吸和心跳所引起的身体表面微动信息进行人体目标检测［4］。脉冲超宽带（Impulse Radio Ultra Wide Band，IR-UWB）雷达是通过雷达发射端发射电磁波，利用传播介质到达人体，电磁波脉冲经过人体的散射产生相应的回波信号，回波信号通过介质传播到雷达接收端，随后被接收端接收进行数据采样。与微波多普勒雷达相比，IR-UWB 雷达的功耗更低、尺寸更小和信噪比（Signal-to-Noise Ratio，SNR）更高，在复杂环境下具有抗杂波、高鲁棒、高精度等特性［5-6］，可检测人体内部的宏观和微观运动［6］。文献［7］针对IR-UWB 信号在穿墙过程中由墙体参数估计误差所导致的时间误差问题，提出基于图像使用迭代算法的目标范围估计方法。文献［8］介绍了微波多普勒雷达是一种非接触式检测生命体征的替代方法［9］。但是，多普勒雷达系统难以穿透材料以及存在零点问题［10］。IR-UWB 雷达信号由于良好的材料穿透性，因此可以轻易地穿透墙体，进行生命体征的检测和目标识别［11-12］。

人体呼吸会引起人体胸腔壁微动，产生微弱的呼吸回波信号。IR-UWB 雷达系统采集的原始回波信息中通常包含线性趋势、静态杂波、谐波干扰等干扰信号，近些年国内外研究人员对此进行了大量研究以抑制这些杂波信息。文献［13］使用自适应杂波消除技术消除类似呼吸的大量杂波。文献［14］通过快速傅里叶变换（Fast Fourier Transform，FFT）研究人体呼吸回波信号中的时域特征。文献［15］采用有限差分时域数值模拟方法成功模拟了地震灾害后被困人员的心跳、呼吸等生命体征信息。文献［16］提出一种复杂度低的最大似然（Maximum Likelihood，ML）估计方法来估计加性高斯白噪声（Additive White Gaussian Noise，AWGN）中的人体呼吸周期。文献［17］采用奇异值分解在低信噪比条件下提取人类呼吸信号的相关信息。文献［18］利用回波经验模式分解（Empirical Mode Decomposition，EMD）提取雷达回波信号，随后通过独立主成分分析和杂波抑制对雷达穿墙检测进行研究。文献［19］使用复信号解调来消除杂波。文献［20］通过时域自相关技术、快采样均值滤波算法对信号作降噪处理，提高回波信号信噪比。针对现有非接触式呼吸检测方法难以根据低信噪比的接收信号准确估计出人体呼吸频率和到达时间（Time of Arrival，TOA）范围的问题，本文提出一种有效的非接触式呼吸检测方法。

1 IR-UWB 雷达与呼吸回波模型

1.1 IR-UWB 雷达原理

在对呼吸运动引起的胸腔表面的微动信息进行建模的过程中，不论是室内还是室外环境，都存在各种干扰信息、噪声以及多径效应的影响。IR-UWB 雷达接收到的原始回波会包括许多无用的信息，因此要将呼吸信号从含有众多干扰信号的原始回波中提取出来，如图1 所示。实验对象为一个人相对静止地坐在一个高40 cm 的椅子上，面朝置于桌子上离地80 cm 的IRUWB雷达设备，雷达的发射天线（Transmit Antenna，TX）位于设备的顶端，相应的雷达接收天线（Receive Antenna，RX）位于设备的底部。

图1 基于IR-UWB 雷达的呼吸信号提取Fig.1 Respiration signal extraction based on IR-UWB radar

IR-UWB 雷达利用雷达发射端发射电磁波，通过传播介质到达人体胸腔表面，随后经过人体的反射、散射形成雷达回波信号，回波信号经过传播介质到达雷达接收端，然后被接收端接收。通过IRUWB 雷达，可以从接收信号的传播延迟变化中检测到受试目标。电磁波脉冲经发射天线发射出来后接触人体形成反射脉冲，通过反射脉冲的振幅变化以及到达时间可以进行胸腔微动信息评估，然后从中分析得出呼吸频率、幅度信息以及目标范围。收发天线到被检测目标的距离［5］可表示如下：

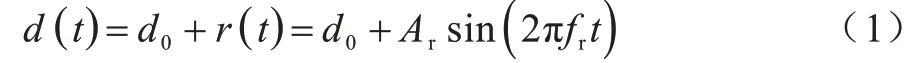
其中：d0表示收发天线到人体胸腔的标称距离；Ar表示呼吸的位移幅度；fr表示呼吸频率。若归一化接收脉冲用δ(t)表示，则总脉冲响应可表示如下：

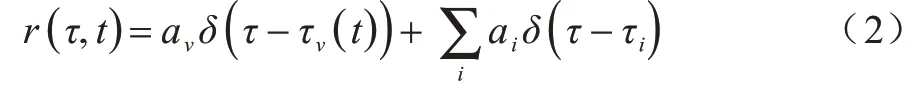
其中：t表示观测时间；τ表示传播时间；avδ(τ-τv(t))表示由胸腔璧的微小运动所形成的传播时间为τv(t)、幅值为av的脉冲响应；表示由每个静态目标i在传播时间为τi、幅值为ai时所产生的单个脉冲响应的总和。传播时间如式（3）所示：

其 中：τ0=2d0/C；τr=2Ar/C；C表示光 速，为3.0×108m/s。接收到的IR-UWB 雷达信号可表示如下：

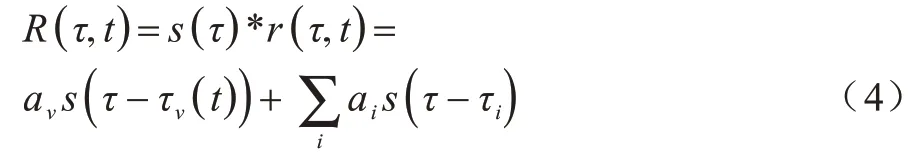
其中：s(τ)表示传播信号；*表示卷积操作。

1.2 呼吸回波模型

IR-UWB 雷达信号采样过程中需对时域信息进行采样，采样时通常涉及两个时间轴：1）快时间域，即单个脉冲信号传播时域信息的时间轴；2）慢时间域，即用来表示脉冲之间的先后关系的时间轴。为简化模型，假设在理想情况下，即忽略静态回波及其他杂波，式（2）可转化为如下离散时间二维回波矩阵（m×n矩阵）：

其中：m和n分别代表慢时间域和快时间域的采样数；Ts和Tf分别表示慢时间域和快时间域的采样间隔。图2 给出了呼吸回波模型的动态特征，使用行向量记录一定小范围内不同观察时间的接收信号，利用列向量记录从不同距离反射的一个脉冲，其中虚线框表示目标所在的检测范围。从图2 可以看出：胸腔璧在快时间域上周期性移动；在慢时间域上，t和t+1T 具有相似的波形。

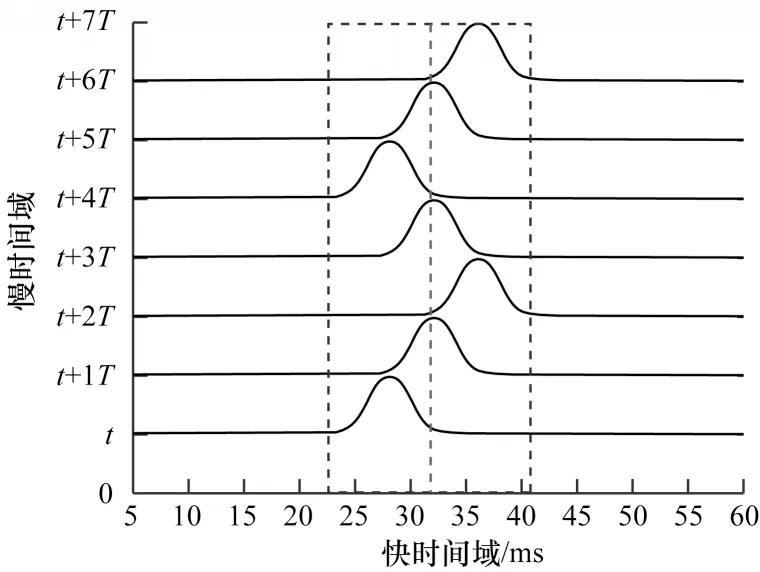
图2 呼吸回波模型的动态特征Fig.2 Dynamic characteristics of the respiration echo models

式（5）经过离散化可表示如下：

其中：δT表示快速采样时间间隔；TS表示持续脉冲时间；m为快时间域的采样数；n为慢时间域的采样数；δR=vδT/2；h[m,n]表示人体微动信号；c[m]表示静态杂波。在实验过程中，接收信号中还可能包含线性趋势、AWGN、非静态杂波及其他未知杂波，因此接收信号可表示为如下：

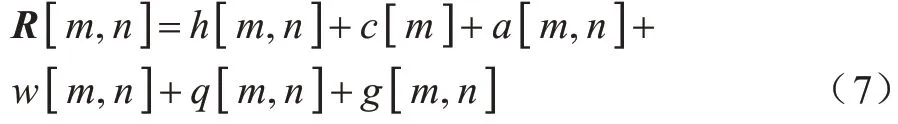
其中：a[m,n]表示线性趋势；w[m,n]表示AWGN；q[m,n]表示非静态杂波；g[m,n]表示其他未知杂波。

在静态环境中，去除所有杂波后的理想雷达回波可表示如下：

为获得呼吸频率fr，在每个慢时间域上对R(τ,t)进行傅里叶变换（Fourier Transformation，FT），如式（9）所示：

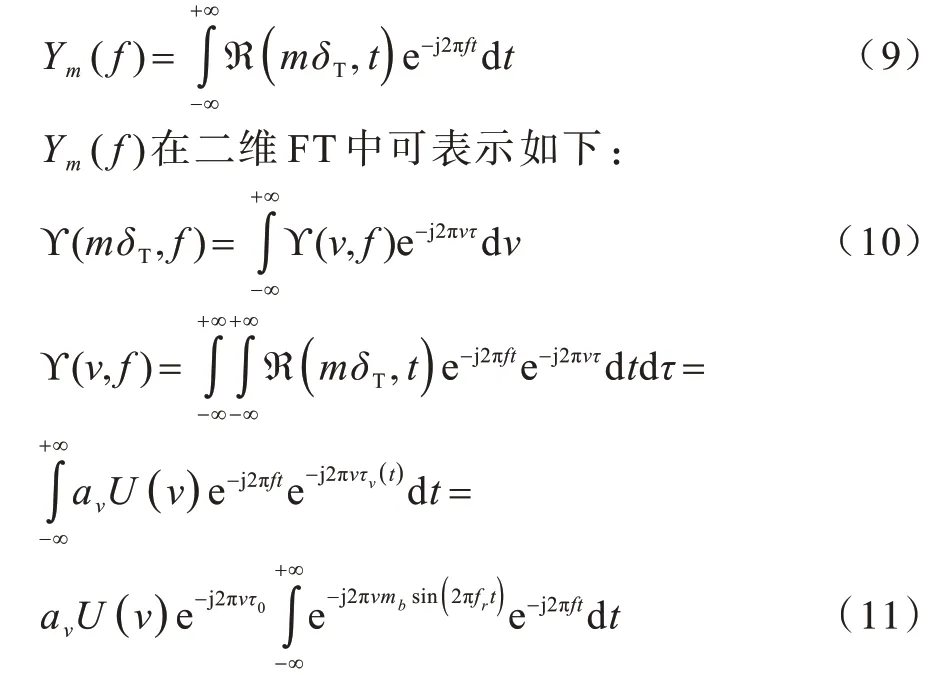
其中：U(v)为快时间域经过FT 后的IR-UWB 脉冲；f和v分别表示慢时间域和快时间域的频谱。基于贝塞尔函数，ϒ(v,f)可表示如下：

通过式（16）和（17）可求解得到呼吸频率fr。

2 基于IR-UWB 雷达的非接触式呼吸检测

首先，对原始IR-UWB 雷达回波信号进行线性趋势消除。然后，通过两个五阶巴特沃斯滤波器对其进行滤波，并使用平滑滤波器得到平滑的采样回波信号。对采样回波信号在慢时间域内进行FT 后通过窗口选择，对受试目标进行呼吸频率估计，同时对采样回波信号使用基于雷达回波信号的超值峰度（Excess Kurtosis，EK）与均方根（Root Mean Square，RMS）的TOA 范围估计算法（简称为EK-RMS 算法），得到受试目标的TOA 范围。最后，将呼吸频率和TOA 范围的目标信息进行比对，得到受试目标的呼吸频率。基于IR-UWB 雷达的非接触式呼吸检测流程如图3 所示。

图3 基于IR-UWB 雷达的非接触式呼吸检测流程Fig.3 Procedure of non-contact respiration detection based on IR-UWB radar

2.1 静态杂波去除

IR-UWB 雷达接收到的回波信号除了包含被测目标的信号以外，还包含周围环境经反射、散射所接收到的信号，其中静态杂波是一个显著的影响因素，可表示如下：

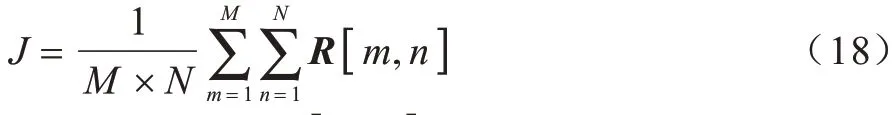
从回波信号R[m,n]中消除静态杂波得到Ω[m,n]：

使用LTS 算法可有效消除回波信号中的线性趋势［17］：

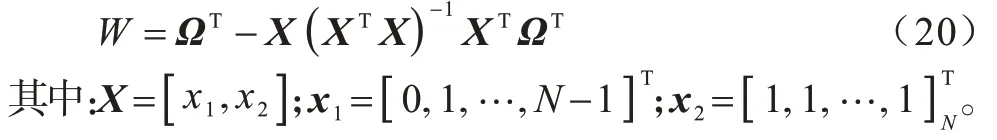
2.2 杂波抑制

IR-UWB 雷达回波信号是由实验环境、检测目标与天线的方位角、介电常数、湿度以及电磁波极化所共同决定的［21］，由于这些参数会随着环境变化很能准确预测，因此本文使用巴特沃斯滤波器进行估计，n阶巴特沃斯滤波器的幅度和频率关系可表示如下：

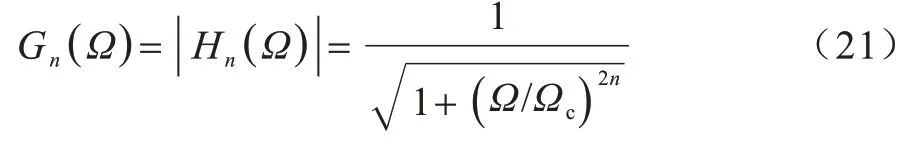
其中：G表示滤波器的放大率；H表示传递函数；n表示滤波器的阶数；Ω表示信号的角频率；Ωc表示截止频率。巴特沃斯滤波器阶数越高，幅频特性越好，即滤波器性能越好，计算复杂度越高。通过前期大量实验验证得出，滤波器阶数选择为五阶，即n=5 时，具有良好的滤波效果，同时考虑到计算复杂度，选择一个五阶巴特沃斯低通滤波器和一个五阶巴特沃斯高通滤波器，分别设置截止频率Ωc为0.103 7 和0.022 2。归一化截止频率可表示如下：

其中：fs表示在快时间域内的采样频率，在每个索引记为n的慢时间域周期内，均对快时间域上的脉冲回波信号Wm×n进行滤波，滤波后得到：

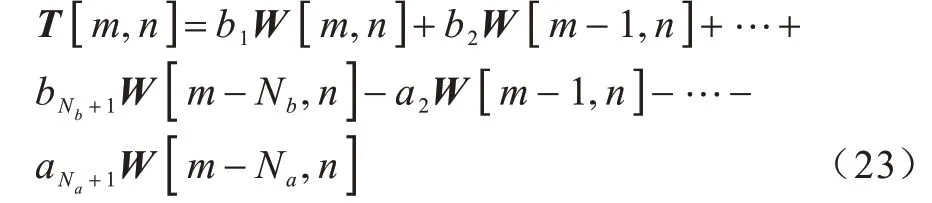
因为使用五阶巴特沃斯滤波器，所以设置Nb=Na=5，其中ai和bi表示滤波器系数。本文采用平滑滤波器抑制非静态杂波：

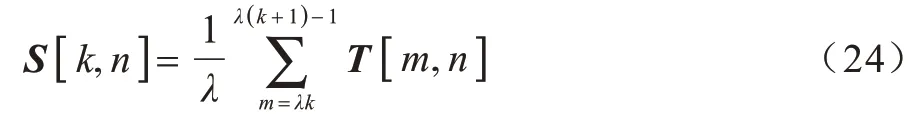
2.3 TOA 范围估计

经过滤波处理后，大部分杂波得到抑制，高斯噪声w[m,n]是影响呼吸回波信号的主要因素。频谱峰度可用于提取非高斯信号，还可以确定其在频率中的位置。本文基于雷达回波信号的超值峰度与均方根对目标进行TOA 范围估计。下面给出每个快速时间域为m的EK：

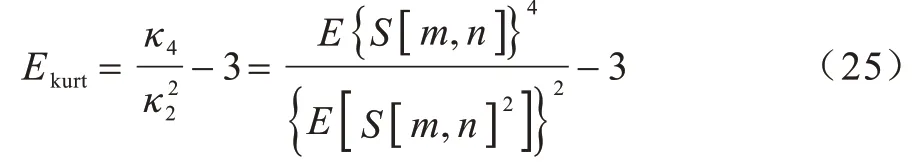
其中：κ4、κ2分别表示样本的四阶中心距和二阶中心距；E表示样本期望。S[m,n]和EK 的RMS 表示分别如式（26）、式（27）所示：

短时傅里叶变换（Short Time Fourier Transform，STFT）和小波变换（Wavelet Transform，WT）已被广泛应用于生命体征信号分析，然而由于STFT 主要依赖信号的时间宽度进行分析，在实际实验过程中时间宽度是很难确定的，因此本文选取在时域中具有可扩展性的WT 进行信号分析。WT 适用于非平稳信号的分析，且窗口尺寸可变。若给定时域信号T(τ)，则连续WT 可以表示如下：

为从回波信号中获取目标对象的TOA 范围估计，频率窗口宽度设置为0.6～1.2 GHz，则受试目标与IR-UWB 雷达之间的距离估计如下：

其中：表示对应矩阵最大的TOA 估计。

2.4 呼吸频率估计

由于IR-UWB 雷达发射脉冲经过人体反射会形成原始雷达回波，原始雷达回波中存在大量杂波信号，为验证EK-RMS 算法对这些杂波信号的抑制或消除作用，进行算法性能分析，截取受试者A 在室外空旷环境下1 m 处所采集到的IR-UWB 雷达回波信号，归一化幅度后的频谱图如图4 所示。

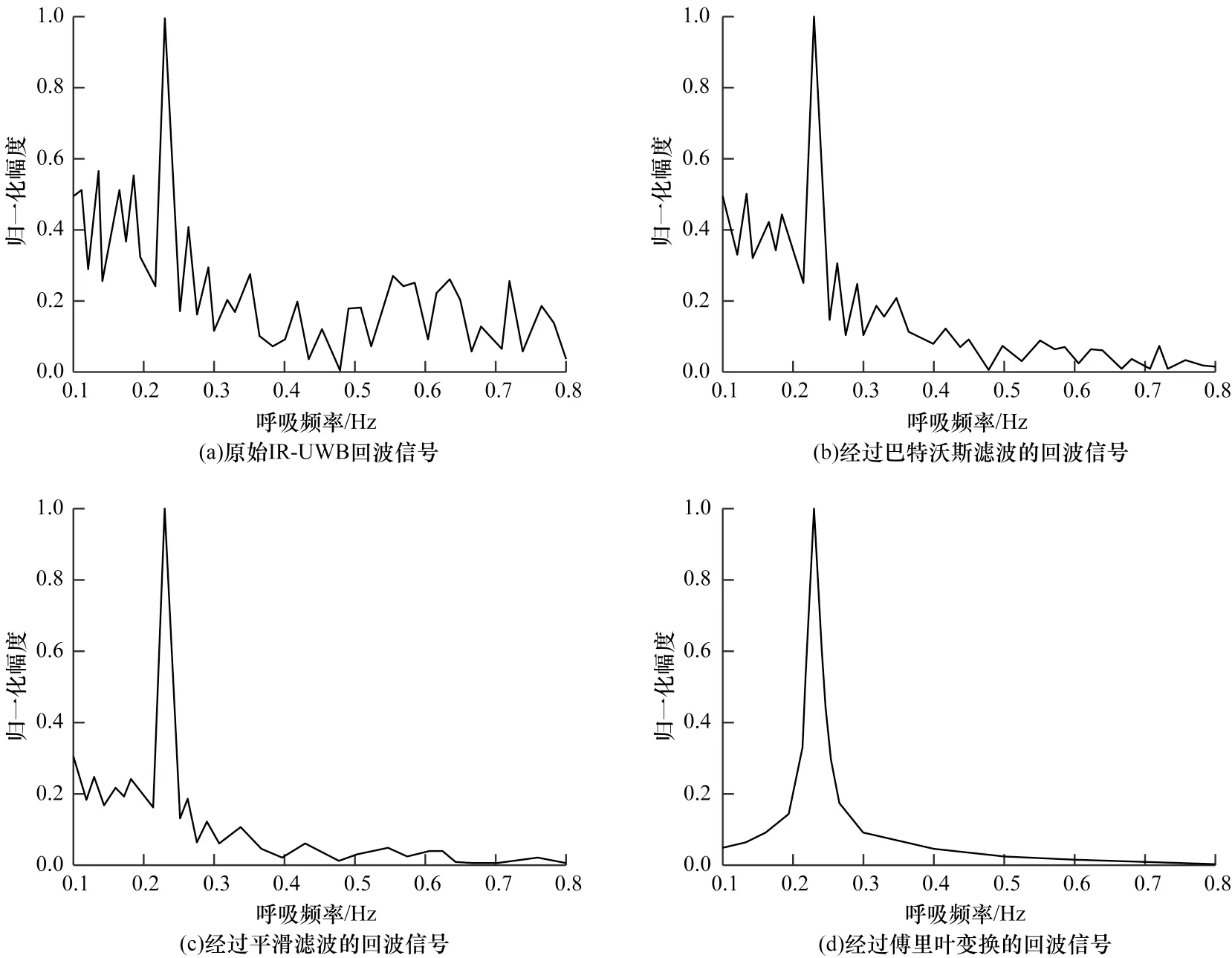
图4 信号处理频谱图Fig.4 Signal processing spectrogram

由图4 可以看出，原始IR-UWB 回波信号含有大量杂波，基于EK-RMS 算法对原始回波信号进行巴特沃斯和平滑滤波后，大量杂波信号得以抑制，最终经过傅里叶变换的呼吸频率在0.229 7 Hz 处幅值达到峰值，可以得出该受试者的呼吸频率约为0.229 7 Hz。

3 实验与结果分析

3.1 数据处理

实验由1 个由Novelda 开发的X4M02 IR-UWB雷达和1 台笔记本电脑组成。IR-UWB 雷达由发射天线、接收天线、雷达模块、微控制单元（Micro Controller Unit，MCU）、存储单元和供电单元组成，如图5 所示。

图5 IR-UWB 雷达实物图Fig.5 IR-UWB radar diagram

3.1.1 实验设备

IR-UWB 雷达发射机带宽为1.4 GHz，传感器中心频率为7.29 GHz，接收器以23.328 GS/s 的速度接收回波信号，并且可以连续覆盖5 m 的探测距离。雷达设备包括处理器、内存、数字基带、模拟前端、脉冲发生器、低噪声放大器（Low Noise Amplifier，LNA）、收发端、电源管理单元（Power Management Unit，PMU）和串行 外设接 口（Serial Peripheral Interface，SPI）。脉冲发生器产生高频脉冲，并在处理器的控制下通过发射天线发出，到达人体胸腔后产生回波，由接收天线接收雷达回波，IR-UWB 雷达发射脉冲的时间间隔由脉冲重复频率（Pulse Repetition Frequency，PRF）决定。

数据采集端为1 台Intel i5-9500 CPU、内存为8 GB 的笔记本电脑，笔记本电脑通过USB 接口与雷达控制模块相连接，进行数据采集并向雷达MCU 发送控制命令。

3.1.2 实验环境

本文分别在室内空旷、室外空旷以及室内复杂环境下对4 名受试者（2 男2 女）通过IR-UWB 雷达采集回波信号，并对收集到的回波信号进行处理分析，使用本文所提出的EK-RMS 算法进行受试目标的呼吸频率和TOA 范围估计。

室内复杂环境选择噪声干扰较多的实验室，实验室有办公桌、板凳、电脑等家居，大小为5 m×5 m；室内空旷环境选择比较空旷的教学楼一楼大厅，大小为5 m×5 m；室外空旷环境选择室外无人的花园，大小为5 m×5 m。实验环境如图6 所示，采取数据的IR-UWB 雷达放置在一个高80 cm 的三角架上。实验过程中受试者保持相对静止，坐在一个高40 cm的板凳或台子上，受试者胸腔离地80 cm，并且上身保持挺直胸腔面对IR-UWB 雷达进行均匀呼吸。

图6 实验环境设置Fig.6 Setting of experimental environments

3.2 结果分析

在采集IR-UWB 雷达数据时，不同的实验环境、测量距离、实验人员等因素都会对回波信号产生影响。本文通过设计多组对比实验，测试EK-RMS 算法性能。4 名受试者的基本信息如表1 所示，对4 名受试者使用呼吸绑带测量20 min 内的呼吸次数并计算平均呼吸频率。

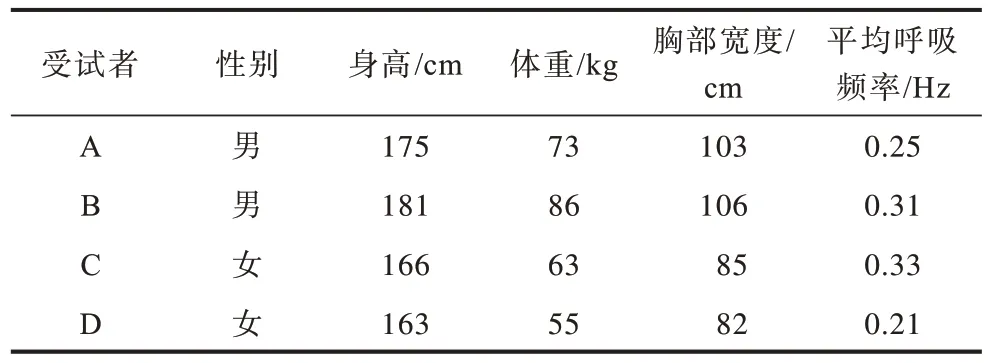
表1 受试者基本信息Table 1 Basic information of subjects

IR-UWB 雷达数据采集设置PRF 为600 kHz、平均采集数量Na为30。通过6 个片段同时进行采样，每个片段的时间窗口设置为124 ms、采样数N为682，快时间域内的样本数量N×6=4 092，因此每个脉冲信号接收时间为N×Na/PRF=0.034 1s，在60 s 内可接收1 759 个脉冲。在室内复杂、室内空旷和室外空旷实验环境中，4 名受试者面朝雷达坐着，保持均匀呼吸，距离雷达1 m、2 m、3 m、4 m 和5 m 的地方进行数据采集，每组数据分别采集5 次，每次采集有效数据时长为20 min。

3.2.1 探测距离对呼吸回波信号的影响

为探究受试者距IR-UWB 雷达设备的远近对呼吸回波信号的影响，设计对照实验，在室内复杂、室内空旷和室外空旷实验环境下，受试者A、B、C 和D分别距离IR-UWB 雷达1 m、2 m、3 m、4 m 和5 m 的情况下进行呼吸频率估计，实验结果如图7 所示。由图7 可以看出，在同一个环境下目标距离雷达相同的距离时，所估计呼吸频率与平均呼吸频率变化基本一致，但是随着受试者离雷达的距离增加，所估计的数据误差增大。

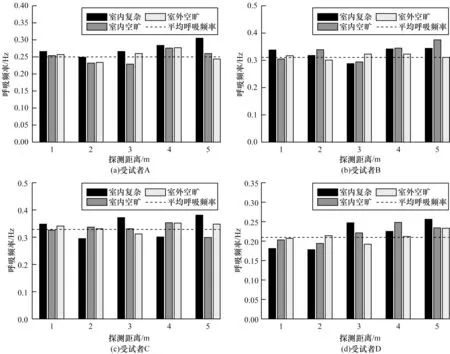
图7 受试者呼吸频率估计Fig.7 Estimation of respiration frequency of subjects

在3 种不同的实验环境下计算并比较4 名受试者的呼吸频率和TOA 范围在距离IR-UWB 雷达1 m、2 m、3 m、4 m 和5 m 时的平均估计误差，结果如表2 所示。由表2 可以看出，探测距离增大，估计误差也逐渐增大。经计算探测距离分别为1 m、2 m、3 m、4 m 和5 m 时，呼吸频率的平均估计误差分别为3.92%、4.59%、4.67%、5.82%和6.74%。在探测距离为1 m 时误差最小，在平均估计误差为2.99%的室外空旷环境下所估计的呼吸频率值更加平稳，更加接近平均呼吸频率。当探测距离为1 m、2 m 和3 m 时，呼吸频率的估计误差最小且在5%以内，究其原因为IR-UWB 雷达发射脉冲受到的干扰更小。由表2 还可以看出，随着受试目标距IR-UWB 雷达的距离增加，TOA 范围的估计误差也逐渐增加。当探测距离为1 m、2 m、3 m、4 m 和5 m 时，TOA 范围的平均估计误差分别约为0.114 m、0.145 m、0.180 m、0.219 m和0.257 m。实验结果表明，使用EK-RMS 算法进行受试目标呼吸频率估计准确率更高，且呼吸频率的平均估计误差约为5.15%，TOA 范围的平均估计误差约为0.183 m。

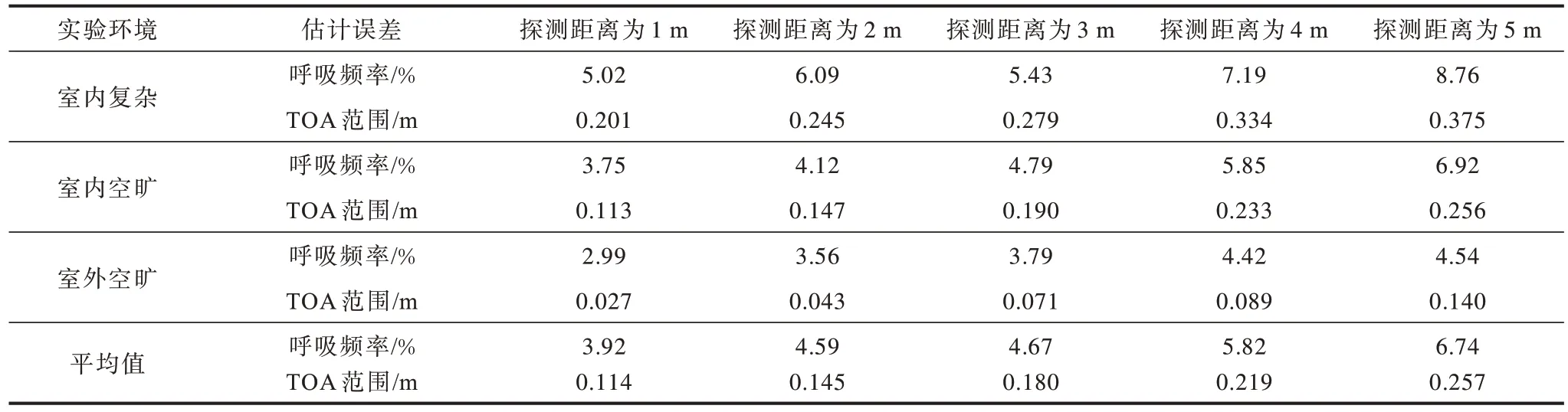
表2 受试者的呼吸频率和TOA 范围估计误差对比Table 2 Comparison of estimation errors of respiration frequency and TOA range of subjects

3.2.2 受试环境对呼吸回波信号的影响

为探究环境对IR-UWB 雷达回波信号的影响，分别在室内空旷环境和室外空旷环境下，对4 名受试者分别在探测距离为1 m、2 m、3 m、4 m 和5 m 的条件下进行呼吸频率估计，实验结果如图8 所示。由图8 可以看出，4 名受试者在室外空旷环境下呼吸频率估计值更加平稳且更接近使用呼吸绑带所测得的平均呼吸频率，受多径效应和环境影响因素干扰，4 名受试者在室内复杂环境下所估计的呼吸频率波动较大。

图8 3 种实验环境下的呼吸频率估计Fig.8 Estimation of respiration frequency under three experimental environments

为进一步验证复杂环境和空旷环境对IR-UWB 雷达回波信号的影响，设计2 组对比实验：1）受试者A 分别在室内复杂环境和室内空旷环境下，进行呼吸频率和TOA 范围估计，实验结果如图9 所示；2）受试者A 分别在室内空旷环境和室外空旷环境下，进行呼吸频率和TOA 范围估计，实验结果如图10 所示。

图9 室内环境下的实验结果Fig.9 Experimental results under indoor environments

图10 空旷环境下的实验结果Fig.10 Experimental results under outdoor environments

第1 组对比实验通过观察受试者A 的呼吸频率估计柱状图可以看出，在室内空旷环境下使用EKRMS 算法相比在室内复杂环境下估计的呼吸频率更加接近平均呼吸频率，误差更小，这是实验所预期的，因为复杂环境干扰较大。通过观察受试者A 的TOA 范围估计图可以看出，使用EK-RMS 算法估计出的TOA 范围误差基本稳定在0.20 左右。室内复杂环境由于多径效应的影响，回波信号中含有大量的杂波，对受试目标的TOA 范围估计造成影响，在室内空旷环境下估计的TOA 范围相比室内复杂环境更加精准、误差更小。

第2 组对比实验通过观察受试者A 在室内空旷和室外空旷环境下估计的呼吸频率，可以看出：室外空旷环境下使用EK-RMS 算法进行呼吸频率估计更加准确，究其原因可能由于室内环境下，钢筋混凝土对IR-UWB 雷达信号有干扰；相比室内空旷环境，在室外空旷环境下使用EK-RMS 算法对受试目标进行TOA 范围估计误差更小。

实验结果表明，EK-RMS 算法具有较高的鲁棒性和准确性，在室内复杂、室内空旷以及室外空旷环境下的平均呼吸频率估计误差分别为6.498%、5.086%和3.860%，平均TOA 范围估计误差分别约为0.287 m、0.188 m 和0.074 m。

3.2.3 室内复杂环境下物品摆放对算法性能的影响考虑到室内复杂环境下不同的物品摆放会对算法性能产生影响，将受试者分别在距离雷达1 m、2 m、3 m、4 m 和5 m 处进行呼吸频率估计，在受试者和雷达之间分别放置实验室常见物品（桌子、凳子、饮水机和电脑），计算呼吸频率估计准确率和误差累计分布函数（Cumulative Distribution Function，CDF）值，实验结果如图11 所示。由图11（a）可以看出，随着探测距离的逐渐增大，算法准确率有不同程度的下降。当受试者和雷达之间放置凳子和桌子时，对雷达回波影响较小。当放置饮水机和电脑时，对雷达回波影响较大，导致算法准确率下降。由图11（b）可以看出，凳子和桌子对算法性能影响较小，饮水机其次，电脑对算法影响最大。通过计算得知，当分别将桌子、凳子、饮水机和电脑放置在受试者和雷达之间时，呼吸频率估计的平均准确率分别约为95.02%、94.45%、93.58%和91.98%。

图11 物品摆放对算法性能的影响Fig.11 The impact of item placement on algorithm performance

3.2.4 算法性能比较

将EK-RMS 算法与FFT 算 法［14］、Phase-Based 算法［22］以及WT-Window 算法［23］进行呼吸频率估计误差对比，实验结果如表3 所示。由表3 可以看出，EKRMS 算法在探测距离为1 m、2 m、3 m、4 m 和5 m 时的呼吸频率估计误差分别为3.92%、4.59%、4.67%、5.82% 和6.74%，相比FFT算法、Phase-Based 算法、WT-Window 算法误差率平均降低了4.424%、3.012%、1.288%，证明了EK-RMS 算法准确率更高。

表3 4 种算法的呼吸频率估计误差对比Table 3 Comparison of estimation errors of respiratory frequency of four algorithms %

图12 给出了4 种算法的SNR，可以看出随着探测距离的增加，4 种算法的SNR 有不同程度的降低，EK-RMS 算法的SNR 稳定于-3～7 dB，明显优于FFT算法、Phase-Based 算法以及WT-Window 算法，证明了EK-RMS 算法具有高鲁棒性，且对杂波信号有明显的抑制或消除作用。

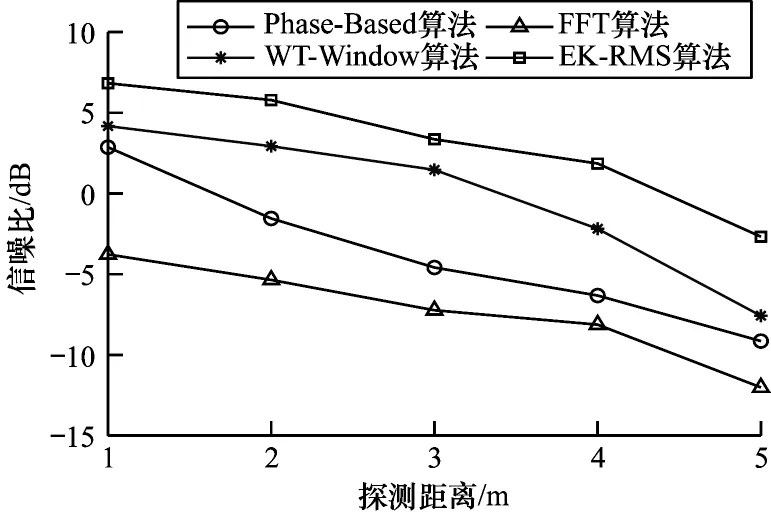
图12 4 种算法的信噪比对比Fig.12 SNR comparison of four algorithms

4 结束语

本文提出一种基于IR-UWB 雷达的非接触式呼吸检测方法，对原始IR-UWB 雷达回波信号进行线性趋势消除，通过五阶巴特沃斯滤波器与平滑滤波器处理得到平滑的采样回波信号，并在慢时间域内对采样回波信号进行傅里叶变换后实现呼吸频率估计。针对受试目标的探测距离不确定问题，采用EK-RMS 算法进行连续小波变换的TOA 估计得到最终受试目标的TOA 范围。实验结果表明，EK-RMS算法能准确提取出受试目标的呼吸特征并获得位置信息，具有鲁棒性强、易于实现等特点。下一步将利用IR-UWB 雷达进行多人生命体征测量，达到实时监测多人呼吸频率和心率的目的。