我的“勾股定理”证明法

文／河南省鹤壁市致远中小学 李双阳

勾股定理占据了几何学的半壁江山。当我刚接触勾股定理时，就被那简单的公式迷住了。

那天，数学老师让我们根据导学案来探究勾股定理的证明方法。导学案上有两个图形，分别是“赵爽弦图”和“毕达哥拉斯证明图”。通过观察，我隐约感觉它们之间有着某种联系。因为数学老师一直教导我们，对于数学一定要有钻研精神，所以我试着把两个图形比较了一下，发现当直角三角形全等的时候，“赵爽弦图”正好可以和“毕达哥拉斯证明图”中间的正方形重合，于是我就把两个图拼到了一起，得到了一个新的图形（如图1）。看着这个熟悉又陌生的图形，我不禁想，这个图是不是也能证明勾股定理呢？

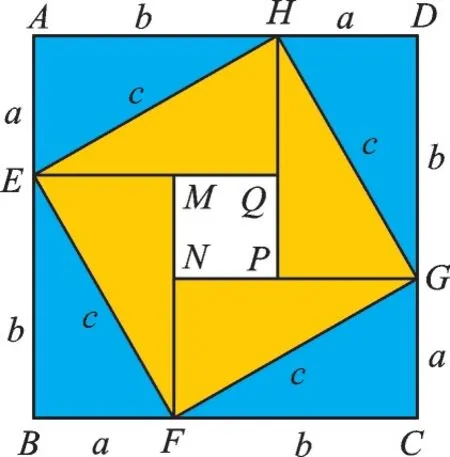
图1

“赵爽弦图”和“毕达哥拉斯证明法”都是根据面积关系列出等式而证明的，所以我猜想，这个新图形应该也可以根据面积来证明。我发现，把每个图形的面积都表示出来比较麻烦，但是结合“赵爽弦图”和“毕达哥拉斯证明法”中的面积表示，就会简单很多。

下面是我的证明过程。

如图1，正方形ABCD由八个全等的直角三角形和一个正方形MNPQ构成，其中，AE=a，BE=b，EH=c。根据“毕达哥拉斯证法”可知，SABCD=（a+b）2，而由“赵爽弦图”可知，SMNPQ=（b-a）2，SEFGH=c2。在图1中，可得SABCD+SMNPQ=2SEFGH，即（a+b）2+（b-a）2=2c2，整理得a2+b2=c2，则证得勾股定理。

通过本次对勾股定理的探索和证明，我受益匪浅，也更加喜欢数学了。数学，真的是一门神奇的学科。一个勾股定理就有这么大魅力，数学中还会有多少美妙的东西等着我们去探索发现呢？

教师点评

小作者善于观察和思考，能在已有知识的基础上，勇于创新，发现不同于我们常用的证明方法，充分体现了数学学习中的创造力，很了不起！