数学，人类的一种文化

文／朱建良 范建刚

同学们，在本章中，我们将一起领略几何学中的一颗光彩夺目的明珠——勾股定理。它被誉为“几何学的基石”，有着悠久的历史，是人类的智慧结晶。

一、数形结合，奇妙完美

相传2500年前，古希腊数学家毕达哥拉斯在朋友家做客时，发现朋友家的地板很有趣，4个全等的等腰直角三角形可以拼成1个正方形（如图1），而且等腰直角三角形两条直角边的平方和等于斜边的平方（如图2）。毕达哥拉斯陷入深思：两条直角边不相等的直角三角形有这个性质吗？于是他着手从特殊到一般，去探究直角三角形三边的数量关系。

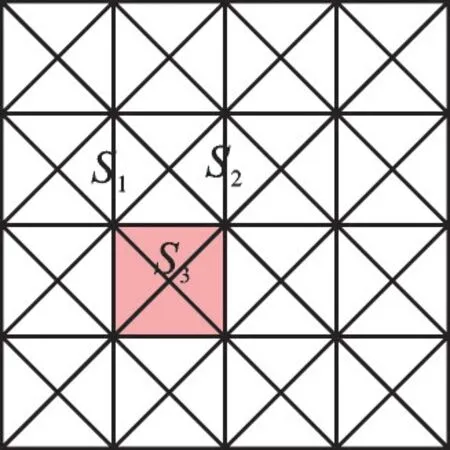
图1

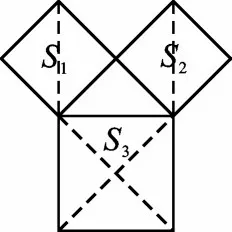
图2

在我国古代，《周髀算经》最早记录了“勾股定理”。同学们，请观察图3，3个正方形的面积分别为a2、b2、c2，你能通过推理计算，体会数与形的完美结合，感悟数与形的内在联系吗（a2+b2=c2）？

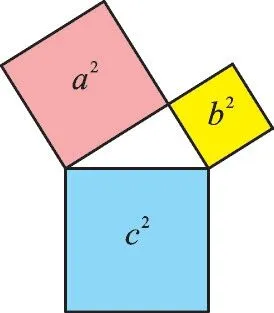
图3

二、出入相补，各从其类

勾股定理有上百种证法，数学家们想方设法去证明它，可见它的魅力所在。

如图4，三国时期东吴数学家赵爽将正方形中的4个直角三角形涂上红色，把中间的正方形涂上白色，经拼补搭配，证明了勾股定理。图5是图4的拼图模型，得到2ab+（b-a）2=c2。魏晋数学家刘徽通过“出入相补，各从其类”，也巧妙地证明了勾股定理（如图6）。“出”表示面积减少，“入”表示面积增加，“出入相补，各从其类”即面积不变，与我们的割补原理类似。这些证明方法都说明了几何方法的多样、灵活和美丽。

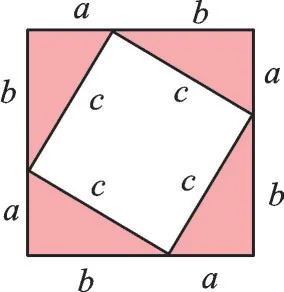
图4

图5

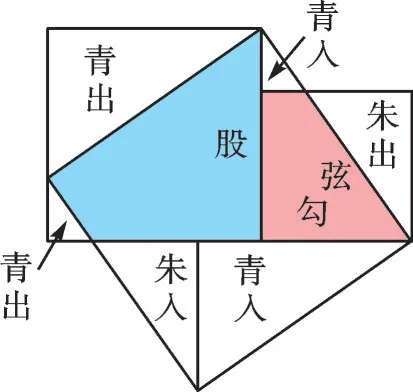
图6

三、以数示形，以形思数

一个三角形满足什么条件才是直角三角形？

古埃及人用13个等距的结，把一根绳子分成等长的12段，一人同时握住绳子的第1个结和第13个结，另外两人分别握住第4个结和第8个结，拉紧绳子，就会得到一个直角三角形，其直角在第4个结处。相传我国古代大禹在治水时也用过类似的方法确定直角。

如图7，在△ABC中，已知a2+b2=c2，△ABC是直角三角形吗？我们先画RtΔA′B′C′，使∠C′=90°，取B′C′=a，A′C′=b，如图8，再根据勾股定理证 明A′B′2=a2+b2，再 用“SSS”证 明△ABC≌△A′B′C′，说明∠C=90°。同学们，要证明一个图形的某种性质，我们可先构造具有这种性质的图形，再证明它与已知图形是“同样的”。这种证明方法称为“同一法”。我们通过“同一法”，可以感受勾股定理蕴含的丰富的数学思想。

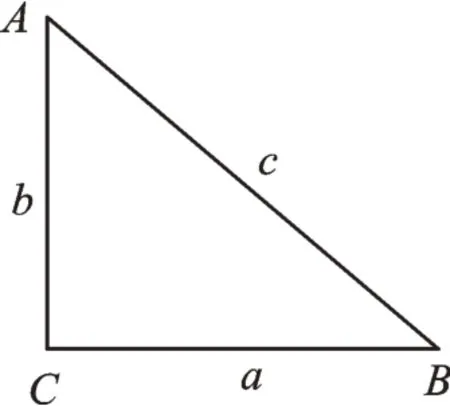
图7

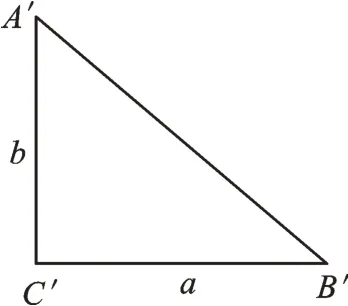
图8

四、学以致用，转化方程

有首歌这样唱道：“波平如镜一湖面，半尺高处出红莲；鲜艳多姿湖中立，猛遭狂风吹一边；红莲斜卧水淹面，距根生处两尺远；渔翁发现忙思考，湖水深浅有多少。”如图9，你能替渔翁计算出湖的水深吗？

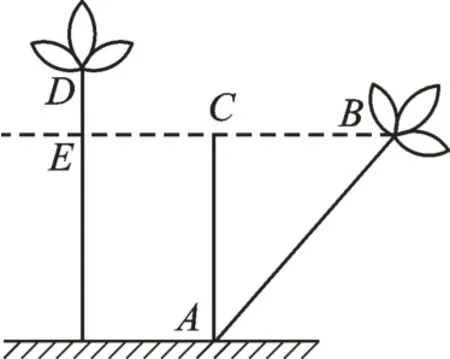
图9

我们设水深为x尺，则AC=x，BC=2，DE=在Rt△ABC中，可列方程，得x=3.75（尺）。我们将实际问题转化成数学模型后，运用勾股定理列出方程，便可解决。

同学们，你们感受到数学证明的优美与精巧了吗？感受到应用勾股定理解决问题后的喜悦与快乐了吗？数学是人类的一种文化，也是人类文明的积淀和传承。让我们一起走进勾股定理，感受它丰富的内涵吧。