基于Levenberg-Marquardt算法的圆柱面拟合研究

秦 锋，张振虎，张 威

(1.三门核电有限公司， 浙江 台州 317112；2.上海勘察设计研究院(集团)有限公司， 上海 200093)

在AP1000(Advanced Passive Pressurized Water Reactor，先进压水反应堆)核电项目核岛安装工程中，一回路主设备安装精度要求很高，例如主泵其安装精度要求优于0.3 mm，且精密对接区域空间狭小、无法通视，传统的高精度全站仪，如徕卡TM50全站仪，无法满足测量精度及通视要求，因此，需要引入更高精度的测量仪器及测量新方法辅助这些设备的安装。激光跟踪仪作为当前精度最高的大范围移动式坐标测量系统，已在飞机制造、高能物理等领域得到了应用。为了确保核岛主设备安装精度，三门核电项目在核电项目中率先采用了激光跟踪仪测量整体建模技术辅助设备精密安装。因核岛主设备外形多为圆柱形，故采用激光跟踪仪测量建模时需要进行圆柱面的精确拟合。圆柱面拟合的关键在于确定圆柱面的轴线和半径。文献[1]通过高斯图法计算圆柱面拟合参数，原理较复杂；文献[2]在文献[1]基础上进行了改进，将高斯图法得到的圆柱面参数作为初始值，并采用非线性最小二乘进行优化计算；文献[3]根据矩阵特征分解、测量坐标系和标准坐标系转换关系提出了按特征值、旋转角和平移量为参数的二次曲面拟合方法；文献[4]基于遗传算法进行圆柱面的拟合；文献[5-8]通过圆柱面在平面上的投影圆度判别估算圆柱面参数初值，然后，采用优化算法或平差方法进行圆柱面拟合；文献[9]先以点到圆柱中轴线距离平方与半径平方之差为对象构造优化函数得到圆柱面参数初始值，再以点到圆柱面的距离为对象构造误差函数进行精确求解；文献[10-11]基于坐标转换的方式进行圆柱面的拟合；文献[12]综合采用了文献[9]和文献[10-11]所述的两种方法；文献[13]采用主成分分析法和线性最小二乘法确定拟合初值，再采用非线性最小二乘法计算圆柱模型参数；文献[14]采用遍历算法通过三点共线法确定圆柱轴线向量初始值，再进行圆柱面参数的精确求解。从以上算法可以看出，拟合圆柱面一般需采用合适的方法估算圆柱面拟合参数初始值，然后再进行参数的精确求解。本文提出了一种基于Levenberg-Marquardt算法(以下简称LM算法)的新方法，该方法不用估算初始值，基于指定的初始值就可以进行圆柱参数的计算。经数据模拟及案例验证，取得了良好效果。

1 数学模型及算法

确定一个圆柱面一般需要圆柱面的中轴线及圆柱的半径，而确定圆柱面的中轴线需要知道中轴线上两点坐标或中轴线方向向量和轴线上的一个点坐标等6个参数，故拟合一个圆柱面需要求解圆柱面中轴线及半径等7个参数。设空间圆柱面其轴线方向向量为(a,b,c)，轴线上一点坐标为(X0，Y0，Z0)，圆柱面上测量数据为(Xi，Yi，Zi)。

1.1 圆柱面数学模型

圆柱面可以用下式表示：

(1)

其中，

A=c(Yi-Y0)-b(Zi-Z0)

B=a(Zi-Z0)-c(Xi-X0)

C=b(Xi-X0)-a(Yi-Y0)

为便于计算，令(a,b,c)为单位向量，即：a2+b2+c2=1。

(2)

上述问题为约束优化问题，求取最佳参数较繁琐。为简化求解，可将约束优化问题转化为无约束优化问题。参考球面坐标系表示方法，令：

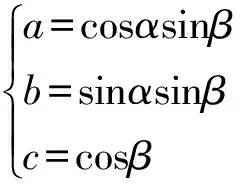
(3)

此外，圆柱面中轴线上有无数点，其中轴线上一点可以任意指定，故其三维坐标的某一坐标可以取任意值，为便于说明，本文中指定Z0为常数。

综上，拟合空间圆柱面原需要计算7个参数(a,b,c,X0，Y0，Z0,R)，经优化后，只需计算5个参数，分别为(α,β,X0,Y0,R)，且将问题转化为以下无条件极值问题：

(4)

1.2 参数求解算法

式(4)为非线性最小二乘问题，根据文献[15]，解决非线性最小二乘问题常用算法有最速下降法、Gauss-Newton算法(GN算法)及LM算法。最速下降法以负梯度方向作为极小化算法的下降方向，是无约束优化中最简单的方法。研究发现，最速下降方向仅是算法的局部性质，对于许多问题，最速下降法并非“最速下降”，而是下降缓慢，特别当靠近极小值时，下降变得非常缓慢。GN算法使用泰勒级数一阶展开式去近似地代替非线性回归模型，然后通过多次迭代，多次修正待求参数值，直至限差达到阈值时终止。GN算法不一定总体收敛，其对于小残量问题有较快的局部收敛速度，对于不是很严重的大残量问题有较慢的局部收敛速度，对于残量很大的问题或非线性程度很大的问题则往往不收敛。LM算法最早由Levenberg[16]提出，在GN算法加入正则化参数改善矩阵条件，后由Marquardt[17]进行了改进。该方法是一种介于梯度下降法和GN算法之间的算法，常用于求解非线性最小二乘问题，在正则化参数大时相当于梯度下降法，参数小时相当于GN算法。在GN算法中，通常要求雅可比(Jacobi)矩阵是满秩的，一旦雅可比矩阵奇异的情况发生，使得算法常常收敛到一个非驻点，LM算法显著地改善了这一情况。在一定条件下，LM算法具有全局收敛性，其具有超线性收敛速度。在解决非线性最小二乘问题上，LM法是最常用的一种算法，故本文选用LM法求解圆柱面拟合参数，其主要分为数据重心化处理、构造函数及求一阶偏导数、指定初值及迭代求解等步骤。

1.2.1 数据重心化处理

为降低数据量级及减少迭代过程中可能出现的矩阵奇异情况，将圆柱面上的数据进行重心化处理。重心化公式如下：

(5)

重心化处理后，圆柱面轴线向量及半径不变，但圆柱面中轴线位置发生了改变，故中轴线上一点变为(x0,y0,z0)，其与重心化处理前圆柱面中轴线上的一点(X0，Y0，Z0)关系为：

(6)

1.2.2 函数构造及求导

以重心化后的圆柱面上的点(xi,yi,zi)到圆柱中轴线的距离与圆柱面半径之差构造函数：

(7)

其中,

A′=cosβ(yi-y0)-sinαsinβ(zi-z0)

B′=cosαsinβ(zi-z0)-cosβ(xi-x0)

C′=sinαsinβ(xi-x0)-cosαsinβ(yi-y0)

W=[α,β,x0,y0,R]T

因圆柱面中轴线上有无数点，其上的一点可随意指定，为方便计算，本文指定z0=0。

令：r(W)=[r1(W)r2(W) …rn(W)]T

对(α,β,x0,y0,R)分别求偏导数，构造雅克比矩阵：

(8)

1.2.3 算法步骤

LM算法如下：

步骤1：选取参数μ0(一般取0.001)，初始点W0∈Rn，容许误差0≤ε≪1，令k:=0；

步骤2：令Jk=D(Wk)，计算g(Wk)=Jkr(Wk)，若‖g(Wk)‖≤ε，停止迭代，输出Wk作为近似极小点；

1.2.4 初始值及终值

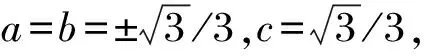
(9)

(10)

1.3 结果评价

圆柱面拟合结果主要通过计算圆柱面圆度及根据圆柱面圆度计算出的均方根误差(Root Mean Squared Error, RMSE)来评价。空间圆柱面的圆度ΔRi为圆柱面表面点到圆柱中轴线的距离与圆柱面半径之差，可以通过式(7)计算。RMSE通过下式计算：

(11)

2 案例分析

2.1 案例1

以激光跟踪仪测量的某设备圆柱面为例，进行圆柱面的拟合，观测的设备圆柱面三维坐标数据如表1所示。

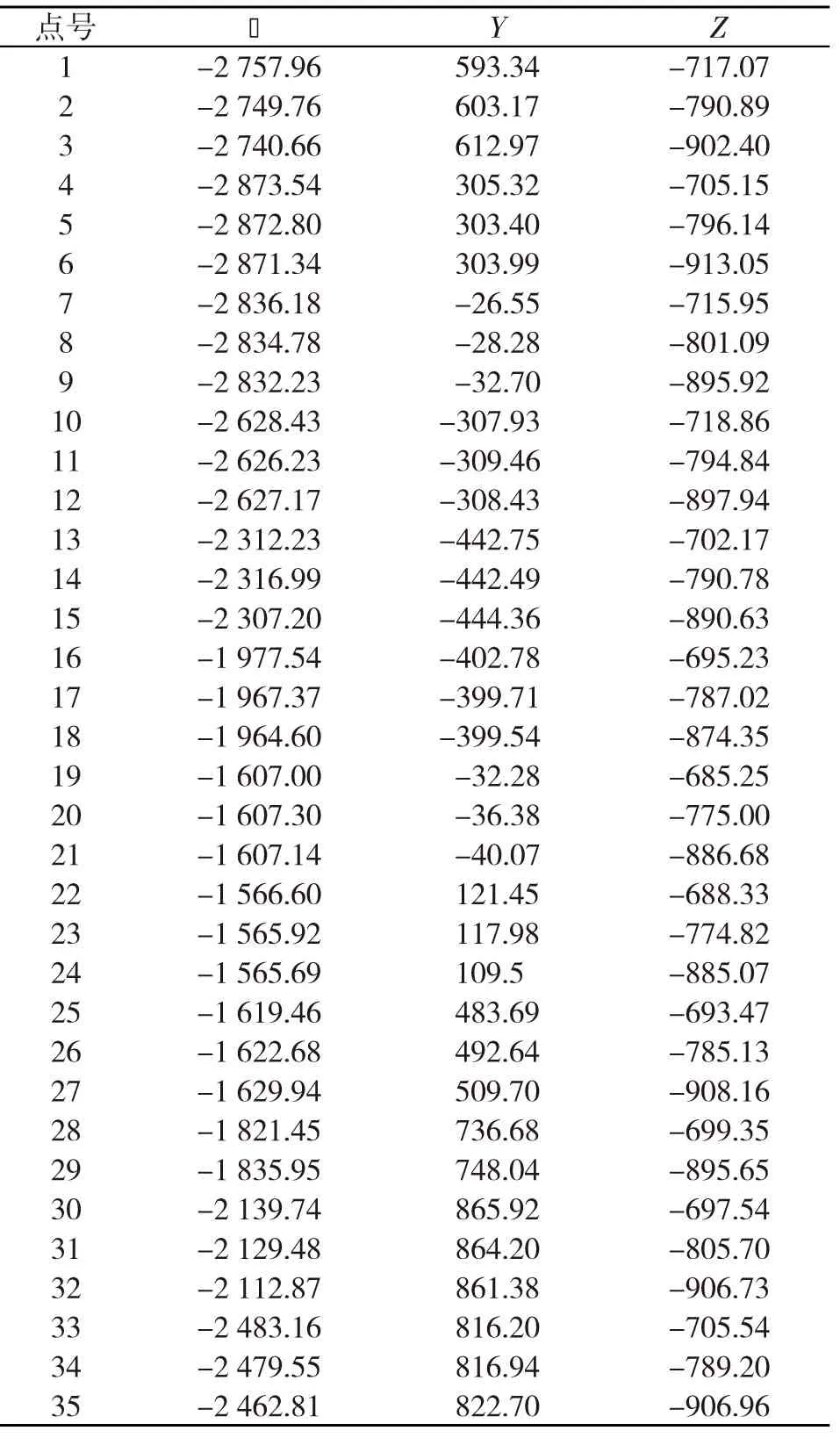
表1 观测点三维坐标/mm

采用本文LM算法计算圆柱面拟合参数，容许误差ε=10-6。经迭代12次后，算法收敛至迭代终止。迭代结果及根据迭代结果计算出的圆柱面参数如表2所示。

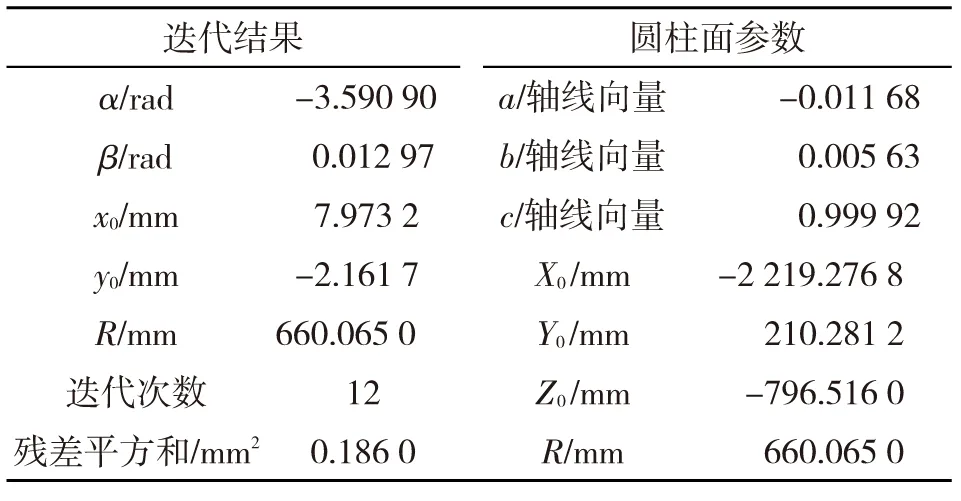
表2 迭代结果和圆柱面参数

根据迭代结果计算出圆度值，圆度值统计如表3所示。

表3 圆度值统计 /mm

为验证本文算法，采用了行业内著名的SA(Spatial Analyzer)测量软件进行计算，计算结果与本文一致。

2.2 案例2

采用文献[4]案例中数据，根据本文算法计算圆柱面拟合参数，容许误差ε=10-6，并与文献[4]和文献[14]计算结果进行对比，相关结果如表4所示。

表4 文献[4]、文献[14] 算法和本文算法结果

经过7次迭代，算法迭代终止。因圆柱面中轴线上一点可以随意指定，为便于与文献[4]和文献[14]中数据对比，将本文计算结果中轴线上一点的X值移动至与文献[4]和文献[14]一致，得到的中轴线上的一点变为(10, 22.649 6, 4.484 3)。对比本文算法和文献[14]算法可以发现，本文算法计算结果和文献[14]中计算结果一致，说明两种算法精度相当。另对比本文算法和文献[4]算法可以看出，本文算法迭代较快，RMSE值较小，这表明本文算法略优于文献[4]算法。

3 工程应用

AP1000主泵为核1级设备，是垂直安装、无密封的单级高惯性离心屏蔽泵，其为核岛反应堆厂房中核心主设备之一。每台机组含4 台主泵，每台主泵可拆卸组件净重约67.4 t，最大外形尺寸为φ2 044.8 mm×5 874.3 mm。在主泵安装过程中，需要先将吸入适配器顶升进入蒸汽发生器底部泵壳内，再将主泵顶升进入吸入适配器中。主泵安装过程中精度要求很高，如主泵扩散器与吸入适配器设计间隙为0.38～0.64 mm，相应地要求测量精度优于0.3 mm。

主泵安装过程中采用了三维整体建模技术，该技术先采用激光跟踪仪采集主泵外形数据以及与主泵匹配的泵壳及吸入适配器外形数据。以主泵测量所用的美国自动精密工程公司(Automatic Precision Industry, API) T3激光跟踪测量系统为例，其角度测量分辨率为0.05″，干涉法距离测量的分辨率为0.1 μm，测量精度1 μm/m；绝对测距精度的分辨率为1 μm，在10 m之内测量精度可以达到15 μm。考虑到激光跟踪仪测量精度很高，且主泵所在房间空间狭小，测量距离不超过5 m，根据文献[18]研究，API公司T3激光跟踪仪全量程点位精度为5 μm/m，整个测量过程实测数据的精度不会超过25 μm，与模型误差相比，实测数据的误差可忽略不计，因此，对主泵圆柱面建模主要考虑建模误差，不考虑实测数据误差。主泵等设备的外形和端面均为圆柱形和圆形，因此，在采集外形数据后需要进行圆柱面和空间圆的建模。对圆柱面的建模采用本文方法进行。根据测量数据，分别建立吸入适配器和泵壳组合模型如图1所示、主泵模型如图2所示。

图1 吸入适配器和泵壳组合模型

图2 主泵建模模型

建模完成后，将主泵模型与泵壳和吸入适配器组合模型进行虚拟装配，计算得出吸入适配器与主泵扩散器之间间隙及位置偏差等，并判断是否满足设计要求。如不满足设计要求，可根据偏差数据进行调整。位置调整可分阶段多次进行，同时在主泵顶升过程中采用激光跟踪仪监测实时间隙。通过精密建模及实时调整，顺利完成了核岛主泵的精密安装，安装过程中未发生任何碰撞，各项偏差均满足设计要求，这也验证了本文建模方法的准确性。

4 结 论

本文基于LM算法，探讨了一种圆柱面拟合方法，该方法参考了球坐标系表示方式，将约束优化问题变成了无约束优化问题，方便了参数计算。该方法不用计算初始值，采用指定初始值，提高了计算效率。经案例及工程验证，该方法精度高、收敛快，可以用于高精度的圆柱面拟合。