自适应短波通信系统跳频信号时差定位方法

孙沙沙，王 鹏

(山东科技大学电子信息工程学院，山东 青岛 266590)

1 引言

短波通信飞速发展，应用价值与日俱增，在远洋商业活动、军事行动、国际组织行为以及人道主义救援等活动中得到广泛应用。尽管初期的短波通信系统具备了一定的跳频抗干扰能力[1]，但是跳频自适应能力欠佳，因此，自适应短波通信系统应运而生，该系统具有短波数据传输任务的通信手段，对军事通信的发展起着不可替代的作用，它不仅对基础设施要求低，而且能使系统在一些恶劣的自然环境中正常工作，不需要依靠中继设备和集线器设备就可以实现远程通信。其中，跳频信号时差定位技术可以有效地定位无线发射器，大大简化测向定位方法，在通信领域具有重要的现实意义。

文献[2]为解决无线通信时差定位技术位置解算下复杂的非线性方程最优化问题，根据实数编码遗传算法，架构改进的自适应遗传算法，基于进化代数增加种群的整体变化与各代种群不同个体适应度的作用，推导自适应交叉率与变异率的运算方法，通过添加最优保存策略避免优良个体破坏、生成新个体，在摆脱局部最优解搜索后，获取全局最优解；文献[3]设计一种基于半定松弛技术的无源定位算法，通过架构传统闭式解的伪线性方程，采用随机鲁棒最小二乘概念、目标参数与额外变量间非线性关系，转换无源定位问题为二次等式约束下最小二乘问题，经过引入半定松弛技术，约束二小二乘问题，利用优化工具箱计算目标参数。文献[4]根据判决在给定的相位区间内的改变形成一个判决序列，提出了一种新的广义似然比检验的最优非相干序列检测算法，对判决序列发生改变处的相位进行排序，并识别出对应区间上的目标序列，实现平坦衰落信道中正交调制信号的最优非相干序列检测。

由于上述文献方法均为无源定位技术，适用性存在局限，为此，本文提出一种自适应短波通信系统的跳频信号时差定位方法，其关键点在于引入互相关函数，减少运算量，省略二维搜索位置过程中的每一次互相关矩阵特征值计算步骤；通过从频域解得跳频信号，降低计算难度，抑制噪声，提升定位准度。

2 自适应短波通信系统跳频信号时差定位

2.1 通信系统短波传播形式分析

自适应短波通信系统的传输特性是跳频信号时差定位的决定性因素，故需要先分析出系统的天波传输信道电离层特性。当距离地面约60km至9000km的大气层处于电离状态时，或者因受到太阳与紫外线综合作用而出现电离情况的高空大气形成了大气层，该大气层区域均为电离层。其离子密度随着高度的改变而发生变化，电离层共分为四层，按照升序排列是：D、E、F1、F2。每一层的特性描述如表1所示。

表1 电离层特性描述

自适应短波通信系统具有多种传播形式，但短波信道会依据电离层的反射情况，选取不同传播形式完成短波传播。

2.2 跳频信号时差定位

2.2.1 信号模型构建

已知某跳频信号源的跳带范围W与每跳带宽B，信号由空间观测站同步采集，观测站数量有L个。根据自适应通信系统的短波传播形式与跳频信号特点，基于平坦衰落信道[5]，用下列表达式描述观测站接收的跳频信号模型：

(1)

式中，第p跳信号为sp(t)，停留时长为Td，与信号s(t)相互独立的零均值高斯白噪声[6]为nl(t)，接收端的相位系数为γl，信号抵达观测站的时延为τl。若取值τ0=0，则时延τl就相当于信号分别抵达第l个与第0个观测站产生的时差，表达式如下所示

τl=

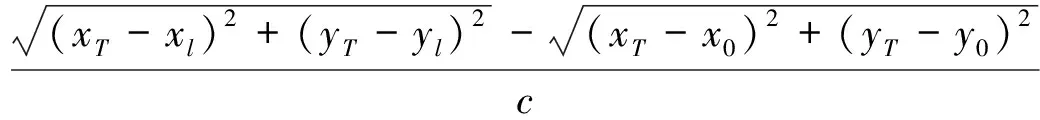
(2)

式中，目标方位为(xT，yT)，第l个观测站方位为(xl，yl)，光速为c。若取值γ0=1，则γl表示针对第0个观测站，第l个观测站接收信号幅度增益。

用Ts指代信号采样间隔，设定采集时间为T，利用下列表达式离散描述采集信号：

rl[n]=rl(nTs)=γls(nTs-τl)+nl(nTs)

(3)

若N个信号采样点的接收信号与跳频信号分别为r[n]、s[n]，则对应的IDFT(Inverse Discrete Fourier Transform，离散傅里叶逆变换)形式如下所示[7]

(4)

频域上分布具有限制性，使跳带W范围中的S[k]值仅存在几个非零值，设定k0，k1，…，kM-1为离散频谱内m个非零值S[k]的对应方位，则将跳频信号s[n]改写为下列表达式

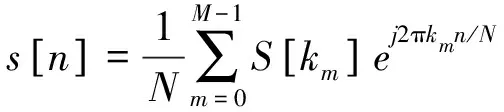
(5)

rl[n]=γlHT(n-τl)Φ+nl[n]

(6)

2.2.2 时差定位

经过信号模型分析，可从观测数据rl[n]中直接获取目标方位，跳频信号模型的似然函数[8]如下所示

(7)

取值上式中的Φ偏导是0，令上式最大化，则采用下列公式求解Φ的最大似然估计

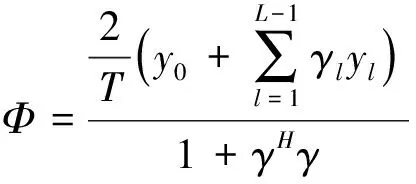
(8)

式中的y0，yi表达式如下所示

(9)

将接收信号r0[n]映射至跳频信号傅里叶基H*(n)，投影为y0，对rl[n]进行τl时差补偿后的投影为yi，根据上式可知，在信息离散的情况下，两者均能够由离散傅里叶变换取得。故改写式(7)为下列表达式

(10)

式中，含噪信号与信号能量之和为首项。因为最大化似然函数与最大化第二项具有相同效果，故推导出下列表达式

(11)

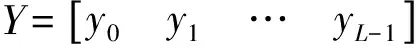
(12)

若想减少运算量，省略二维搜索位置过程中的每一次互相关矩阵特征值计算步骤，需实施以下流程。各观测站与参考站的互相关函数总和计算公式如下所示

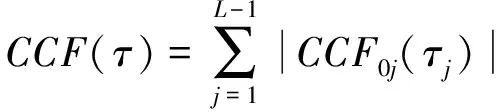
(13)

为降低计算难度，抑制噪声，互相关函数通过下列公式从频域解得跳频信号

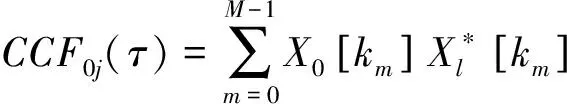
(14)

信号抵达参考站与第j个观测站时差的最大似然估计表达式如下所示

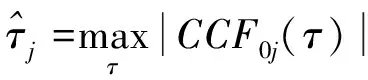
(15)

综上所述，采用下列公式界定跳频信号定位方法

(16)

3 时差定位模拟分析

3.1 实验用自适应短波通信系统构建

选用三个信号接收站与一个控制处理中心构成自适应短波通信系统。信号接收站的组成部分分别是接收采集预处理子系统、天馈子系统以及同步子系统。各子系统与控制处理中心的组件和功能描述如表2所示。

表2 子系统组件与功能描述

采用工作频段是30MHz到3GHz的双锥全向天线，工作频段为30MHz到6GHz的安捷伦射频传感器，目标辐射源选用信号源E4438C与带宽是10MHz的大疆精灵无人机以及遥控器，无人机各时隙长度约为9.9ms，2.4到2.5GHz之间的工作频点是7个；遥控跳频信号的工作频段是2483到2562MHz，共有36个频点，时隙长度为3.61ms，信号带宽为1.5MHz。观测站与辐射源的具体坐标如表3所示。

表3 接收站站址与辐射源坐标统计表

通信系统运行过程中，三个接收前端在收到控制处理中心发起的定位指令后进行同步采集；各接收前端天线接收信号后，传感器将实施滤波、采集以及DDC等射频信号预处理；控制处理中心收到由网络传来的传感器数字信号；后端控制处理中心检测、参数估计以及定位解算所接收的三站数字信号，探测到目标，完成定位。

3.2 实验结果对比分析

3.2.1 信号源信号定位

在已知坐标上安置信号源，连接射频线缆与全向发射天线，经纬度搜索步进是0.00002°，设定信号源频率是2.5GHz，发射信号为5MHz带宽BPSK，功率是10dBm，信号采集单位时间是0.2s，共采集100次。分别采用文献方法与本文方法定位采集的信号，定位结果如图1所示。

图1 信号源信号定位效果对比

根据图1中所示各方法的信号源信号定位结果可知，由于本文方法构建了跳频信号模型，并采用该模型展开了分析，因此，较文献方法定位结果的标准差更小，即本文方法具有更理想的定位精度。

3.2.2 遥控跳频信号定位

在已知坐标上安置无人机遥控器，电源启动后各观测站采集无人机图传信号，经纬度搜索步进是0.00002°，根据传感器的最大工作带宽，设定传感器带宽参数为20MHz，对应采样率的复采样为30MHz，信号采集单位时间是0.2s，共采集100次。分别采用文献方法与本文方法定位采集的信号，定位结果如图2所示。

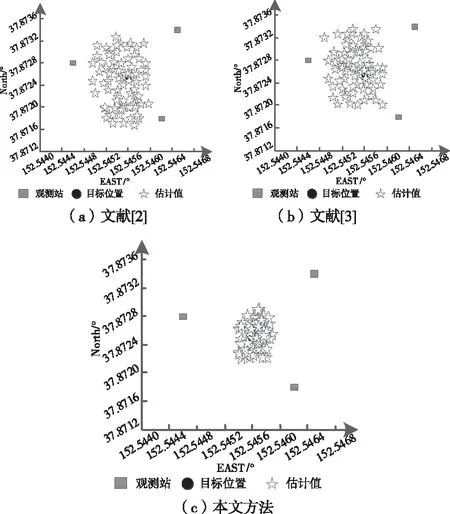
图2 无人机图传信号定位效果对比

根据图2中各方法定位无人机遥控跳频信号结果可知，本文方法因引入了似然函数与最大似然估计，使互相关函数通过频域计算跳频信号，因此，相对比文献[2]、[3]方法，其定位结果标准差相对更小，定位准确性较好。

3.2.3 结果分析

各方法信号源与无人机遥控跳频信号定位结果均说明本文方法的定位性能更加优秀。两种信号定位结果中，由于无人机遥控器带宽较大，接收信号信噪比较高，信号时域占空比超出73%，使增加频差估计精度的积累时间得以提升，令系统频差校正更准确，跳频信号的定位精度更高；而信号源的定位精度相对差一些，原因是信号的信噪比较小，无法精准检测信号，且信号持续时长较短，降低了时域占空比，大幅度缩减同长度采集数据中可用的有效数据个数，这些都对后续定位处理产生了直接影响，另外，每个观测站间的频差估计精度均受积累时间影响，由于较低的信号时域占空比会降低频差估计精度，因此无法很好校正系统频差。

4 结论

1)就自适应短波通信系统，提出一种跳频信号时差定位方法，信号时域占空比超出73%，使增加频差估计精度的积累时间得以提升，令系统频差校正更准确，跳频信号的定位精度更高。

2)针对某些特定场景，探究时差测向混合定位方法，将时差与测向相结合后完成定位，在信号采集单位时间为0.2s时，所以方法的定位结果标准差较小定位精度得到保证。

3)在未来的研究中，需完善与改进时差测量硬件，将不断创新的DSP与FPGA技术融入时差定位方法中。