基于时频图的改进LeNet-5网络轴承故障诊断

亓海征，殷海双

(东北石油大学电气信息工程学院，黑龙江 大庆 163318)

轴承是机械系统中十分重要的部分，它的运行状态关乎整体运行的好坏。通过故障轴承的振动数据进行故障判断愈发地成为一种趋势。轴承故障诊断一般可分如下几步：数据信号处理，特征值提取以及通过特征值对故障进行识别。在文献[1]、[2]中，通过小波包和傅里叶变换对轴承信号进行处理，以便更好地提取振动信号的特征值；文献[3]通过运用多层的稀疏自编码器来对原始的轴承振动数据进行特征值提取；文献[4]、[5]用堆叠式降噪自编码器将轴承信号重新组合，使神经网络更容易对特征值进行分类；文献[6]通过将振动信号的特征值提取和分类整合成一个整体，使一维的卷积神经网络能更有效地进行故障分类。上述几种轴承故障诊断方法运用神经网络避免了人为特征值的提取，但由于输入信号是一维时间序列信号，在非平稳信号特征提取时会导致一定的特征值丢失，并且典型卷积神经网络也难以处理微小特征值。

针对以上问题，本文介绍了一种基于小波时频图的改进LeNet-5网络轴承故障诊断方法。该方法通过构建两条不同的卷积神经网络支路来提高对特征值的提取，并且用时频图作为输入信号，提高对于非平稳信号故障轴承的识别与分类。

1 小波变换及卷积神经网络

1.1 小波变换

(1)

式中:φa,b为分析小波或者连续小波；φ为母小波或者基本小波；a为改变小波形状的伸缩因子；b为小波的平移因子；t为时间。

对任意函数f(t)∈L2(R)的连续小波变换为[8]：

(2)

1.2 卷积神经网络

卷积神经网络的结构主要由3部分构成。

1)卷积层：卷积层主要用来对输入信号的局部特征值进行提取，其数学定义如式(3)所示。卷积实际上是将卷积核作为滤波器来用，即卷积核与某一点周围的点进行点积，得到该点的新值[9]。

xi+1=Wi⊗xi+bi

(3)

式中：xi为输入的特征值；xi+1为经卷积计算后得到的新的特征值；Wi为卷积核权重；⊗为卷积运算符；bi为偏置。

2)池化层：池化层一般与卷积层连接，其主要作用是将卷积层提取的特征信息进行二次选择，从而提取更深层特征。防止过拟合池运算公式为：

(4)

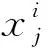
3)全连接层：全连接层的作用是通过连接上层结构，使其能将接收到的信息转换为一维信号，从而能够整理出前面训练结果的差别信息。其计算公式如下：

xl=f2(ωlxl-1+bl)

(5)

式中：xl为全连接层一维信号；ωlxl-1+bl为全连接层的净激活；ωl为全连接层和上一层之间的权重值；bl为偏置系数[10]；f2为全连接层函数。

2 LeNet-5网络模型及其改进

2.1 LeNet-5网络模型

作为一种经典图像识别分类的卷积神经网络结构，LeNet-5网络模型包含卷积神经网络最经典的结构。如图1所示，LeNet-5网络模型包含两层卷积层、两层池化层以及全连接层和输出层。

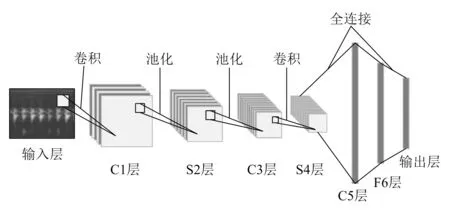
图1 LeNet-5卷积神经网络模型结构

2.2 改进LeNet-5网络模型

为了提升神经网络对微小特征值的提取能力，通过构造两条相对独立的卷积支路来增强对时频图的特征提取，避免特征值提取时因卷积核的原因造成特征值的漏缺，在全连接层能够形成特征互补，使得神经网络能够更好地区分不同的轴承故障。

为了避免在特征值融合部分出现梯度消失的情况，用 ReLU函数代替 Sigmoid 函数作为激活函数，在网络模型最后的全连接层添加在Dropout层，提高网络模型的泛化能力。由于Dropout层的存在，在训练的过程中，会先使得一部分的神经元隐藏。对小批量样本进行随机性训练，经过前向传播与反向传播后，更新网络模型参数，这样可以有效地避免过拟合现象的出现。不加Dropout层时，网络结构的算法：

(6)

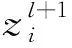
添加Dropout层时，网络结构的算法：

(7)

由于Dropout层的存在，在训练的过程中，会对小批量样本进行随机性训练，经前向传播与反向传播，可以有效地避免过拟合现象的出现。改进LeNet-5网络模型结构如图2所示。

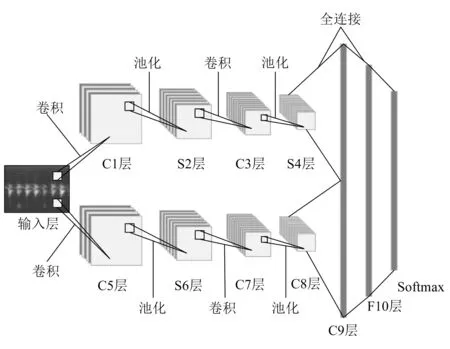
图2 改进LeNet-5卷积神经网络模型结构

2.3 轴承故障诊断流程

图3所示为轴承故障诊断流程，首先对美国凯斯西储大学故障轴承数据集进行预处理，将时序数据分割成小段信号并用one-hot编码为其打上数据标签，通过小波变换将轴承振动原始数据转换为二维时频图并按照比例划分成训练集、验证集和测试集。然后将训练集带入改进LeNet-5网络模型中进行机器学习训练，当训练结果达到收敛时，保存训练好的模型。最后将测试集代入已经完成训练的网络模型中，对网络模型进行故障诊断准确率测试，得到测试集准确率结果。

图3 轴承故障诊断流程

3 电机轴承故障诊断

3.1 数据集的选用和处理

电机振动数据使用的是凯斯西储大学公开的轴承数据集[11]。故障轴承实验装置如图4所示。

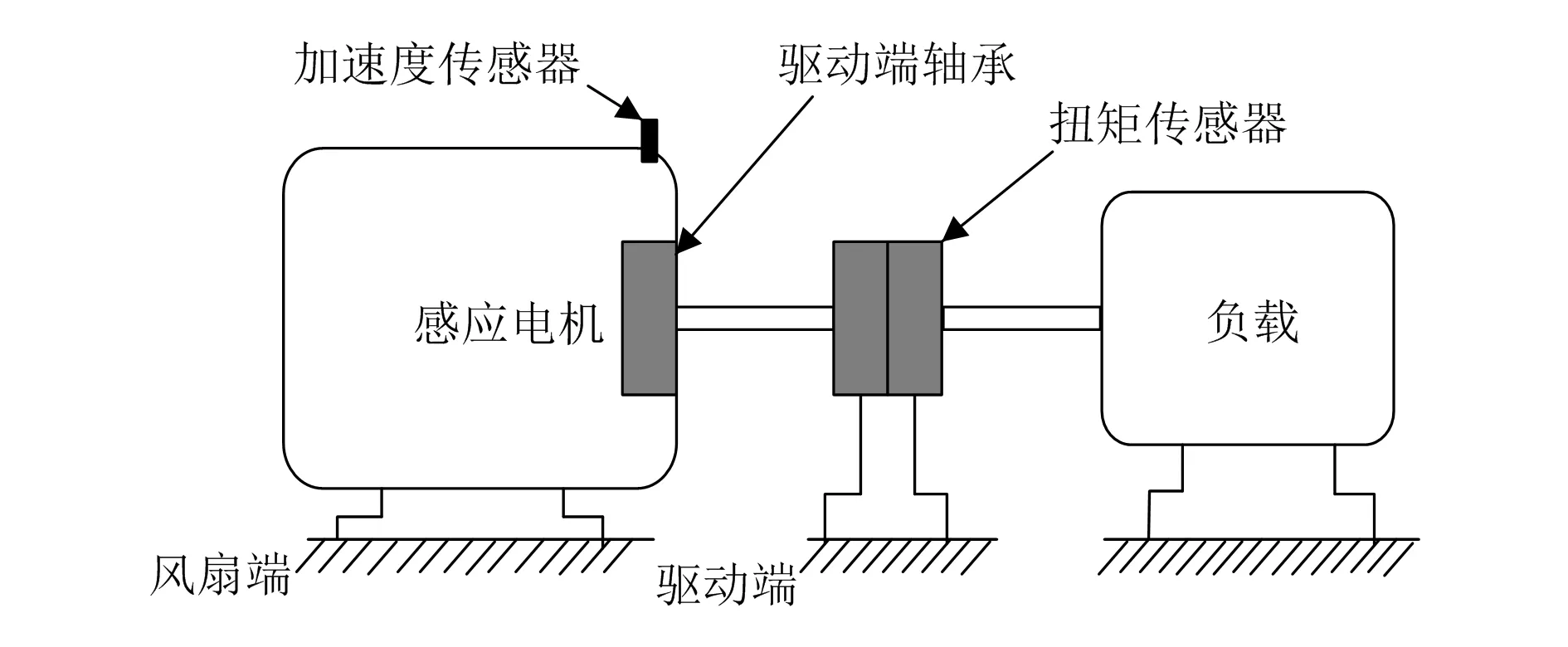
图4 故障轴承实验装置

本文选用的故障类型分为不同直径的内圈、外圈以及滚动体故障[12]。选用cmor3-3作为小波基波对轴承故障数据进行小波变换，经小波变换后，不同状态时频图如图5所示。

图5 不同状态的时频图

3.2 实验验证

在实验验证过程中，先用训练集和验证集对改进LeNet-5网络模型进行训练，再用测试集来验证改进LeNet-5网络模型的准确率。本次实验是在pycharm平台上利用python编程语言实现的，其中使用到的深度学习框架为PyTorch。改进的LeNet网络模型训练结果如图6所示。

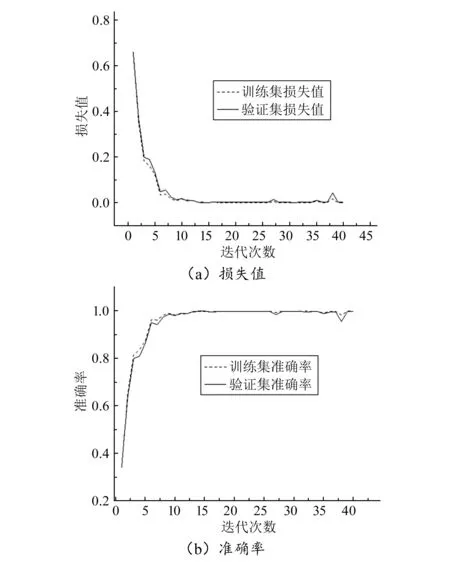
图6 改进LeNet-5网络模型准确率和损失率

根据图6可知，改进LeNet-5网络模型可以正确地进行网络模型训练。经过一定的迭代次数，网络模型可以达到收敛的要求，并且如图5所示，训练集与测试集的准确率都在有效的范围内，且未曾因为数据集过多而出现过拟合的现象。综上可知，改进LeNet-5网络能有效地完成训练并诊断轴承故障。

为验证本文提出的方法相比当前主流智能诊断方法的优越性，将改进LeNet-5网络模型诊断结果与经典LeNet-5网络模型进行对比验证，通过将不同输入信号代入不同的网络模型，对其训练集和验证集的准确率进行对比，准确率对比如图7所示。

图7 3种网络模型下的准确率对比图

由图7可以看出，基于一维信号和二维信号的神经网络结构，在经过一定的迭代次数后，都可以达到收敛的要求，并且训练集与测试集的准确率都在有效的范围内，并未出现因提取的特征值分布与验证集不相同或训练数据过多而导致的过拟合现象。从数据处理上分析，数据经过小波时频变换后，从准确率与丢失率曲线可以看出，相对于一维快速傅里叶变换，经小波变换后的数据在卷积神经网络能够更快地收敛。从网络结构上分析，对于改进LeNet-5网络模型，在收敛速度上相较于经典LeNet-5网络结构能更快地收敛，所需要的迭代次数更少。综上可知，改进LeNet-5网络模型在训练过程中相较于其他的网络模型有更好的性能。

为了进一步证明、对比本文所提诊断方法的有效性，分别将不同网络模型代入测试集进行准确率测试，基于不同网络模型参数的轴承故障诊断准确率如图8所示。

图8 改进LeNet-5网络模型与经典LeNet-5网络模型测试集准确率对比

对于基于一维信号的网络模型，由于需要更多次的迭代训练，因此实验只对照基于二维时频图的不同网络模型。由数据对比可知，改进LeNet-5网络模型的测试集准确率在不同模型参数中都略高于经典LeNet-5网络模型。

4 结束语

经小波变换处理后的二维图像数据在改进LeNet-5神经网络训练中，相较于经典神经网络模型在轴承故障诊断方面有着更好的效果：能在更少的迭代次数下完成收敛并提高了诊断效率；通过特征值融合，使两条支路上的时频图像特征值完成特征互补，提高了轴承故障的准确率。实验结果表明本文所提方法是可行和有效的。