成都双流机场容量与流量分配协同优化的供需平衡策略

何沛南

(中国民用航空飞行学院 空中交通管理学院，四川 广汉 618307)

成都双流国际机场是具备起降大型飞机能力的最高等级(4F级)机场，目前拥有2条平行跑道，是中国八大区域性枢纽机场之一。截至2019年9月，双流机场已开通航线达349条。据2020年7月《民航空管2020年上半年运行统计公报》[1]，双流机场日高峰航班为1 127架。随着空中交通需求连年攀升，交通拥堵和航班延误风险随之不断增大，因此机场的实际容量和极限容量亟待评估。

空中交通管理的一个主要目标是从战略上控制交通流量，以满足机场容量需求但不超过运行容量[2]。随着民用航空运输业的快速发展，空中交通流量需求随之加速增长，而空中交通流量的迅速增长必然会导致空中交通需求与机场容量供给之间的矛盾。由于空域和机场容量有限，空中交通拥堵和航班大面积延误让空中交通流量管理难度日趋增大。因此，研究扩大机场容量[3-5]，以及在不扩大机场容量情况下，研究有效的机场容量与进港和离港容量协同管理技术，是全球业界共同关注的问题[2,6]。

早在20世纪60年代初，美国联邦航空局和机载仪器实验室就编写了容量手册。该手册描述了各种跑道配置下可能的飞机移动(着陆和起飞)的最大数量，以及在不同需求水平上所经历的延误。G.F.Newell[7]研究了飞机离场流与进场流的相互关联，提出采用优化飞机进离场容量的办法来减少拥堵和延误，为探讨机场容量和进离港航班需求平衡优化问题奠定了基础。E.P.Gilbo[2,6]通过对空中交通战略管理相关的机场运行容量研究，提出建立场面容量预估模型和改进方法，为容量评估技术提供了一种解决思路。近年来，Igortimac等[8]利用机场管理策略软件对机场基础设施和地面处理设备的现有容量计算，证明了机场容量优化和最佳机位分配之间的相互依赖性，为容量优化提供了一种科学方法。Alain Urbeltz Isla等[9]认为保证机场运行效率的主要过程之一是航班时刻管理和协调。Joeri Aulman[10]提出，通过对新技术和创新的投资，使用实时数据和预测性计划有助于优化机场容量。Mayara Condé Rocha Murça等[11]指出隔离的平行跑道运行具有更高的跑道容量。Y. Y. Tee等[12]模拟了不同的跑道运行方案并进行比较后验证隔离的平行跑道运行具有更高的跑道容量。P.D.Mascio等[13]认为，采用不同的方法来评估机场基础设施有利于交通流量最大化。S.S.Mohri等[14]指出，如果不考虑机场容量包络曲线会增加航空公司的运营成本。问涛等[15]研究了航班时刻优化模型，用于战略阶段合理安排航班时刻，减少运行阶段航班执行受不确定性因素的影响，提高进离场服务率。沈志远等[16]构建了侧向双跑道系统的跑道容量理论计算模型，用于计算尾流影响下侧向双跑道系统的理论单位时间的容量。亓尧等[17]提出不确定容量下的时隙分配两阶段规划模型，设计了基于人工蜂群(ABC)算法的渐进二元启发式方法来提升求解效率。王春政等[18]提出了一个基于Agent的机场网络延误模型，用于机场网络航班延误预测来应对航班延误问题。据上述文献结论可认为，以机场运行数据为分析对象，以获得机场实际容量为分析基础的机场容量与进离港航班需求之间的关联性并建立数学分析模型具有分析优势和技术可行性。

综上，以不扩大机场容量为条件，本文以成都双流国际机场为例，以历史机场日常容量运行数据为样本，利用包络线可行域来逼近机场实际容量和极限容量。并在此基础上，应用整数线性规划方法建立机场进港和离港容量的协同优化模型，利用遗传算法对模型求解，通过有效利用现有容量资源来满足交通需求来应对空中交通拥堵和延误问题，进而实现机场现有容量资源最大化。

1 机场容量曲线

一般而言，机场容量曲线可以用来表示机场容量。机场容量曲线具有凸函数性质，并满足线性约束条件。因此，机场容量曲线与直角坐标系围成的凸形可行域就是机场容量值域范围，可行域即为机场容量。

本文随机选择了2019年8月中旬的一个日常航班容量运行为样本，采集0:00-24:00时间区间机场航班容量需求和实际进港、离港数据，数据真实完整。据《2019年民航机场生产统计公报》[19]显示，双流机场2019年总起降航班 366 887架次，日均 1 005架次。由于机场每年航班运营高峰期在7～8月份，因此，所选择的月份及航班数据具有代表性和真实性。

成都双流机场进港和离港航班容量需求及执行情况详见表1。进港和离港总需求为1 022架，其中进港需求为513架，离港需求为509架。由于交通拥堵和延误原因被取消的航班有27架，其中进港航班16架，离港航班11架。总的执行航班995架，其中实际进港航班497架，实际离港航班498架，执行率97.36%。

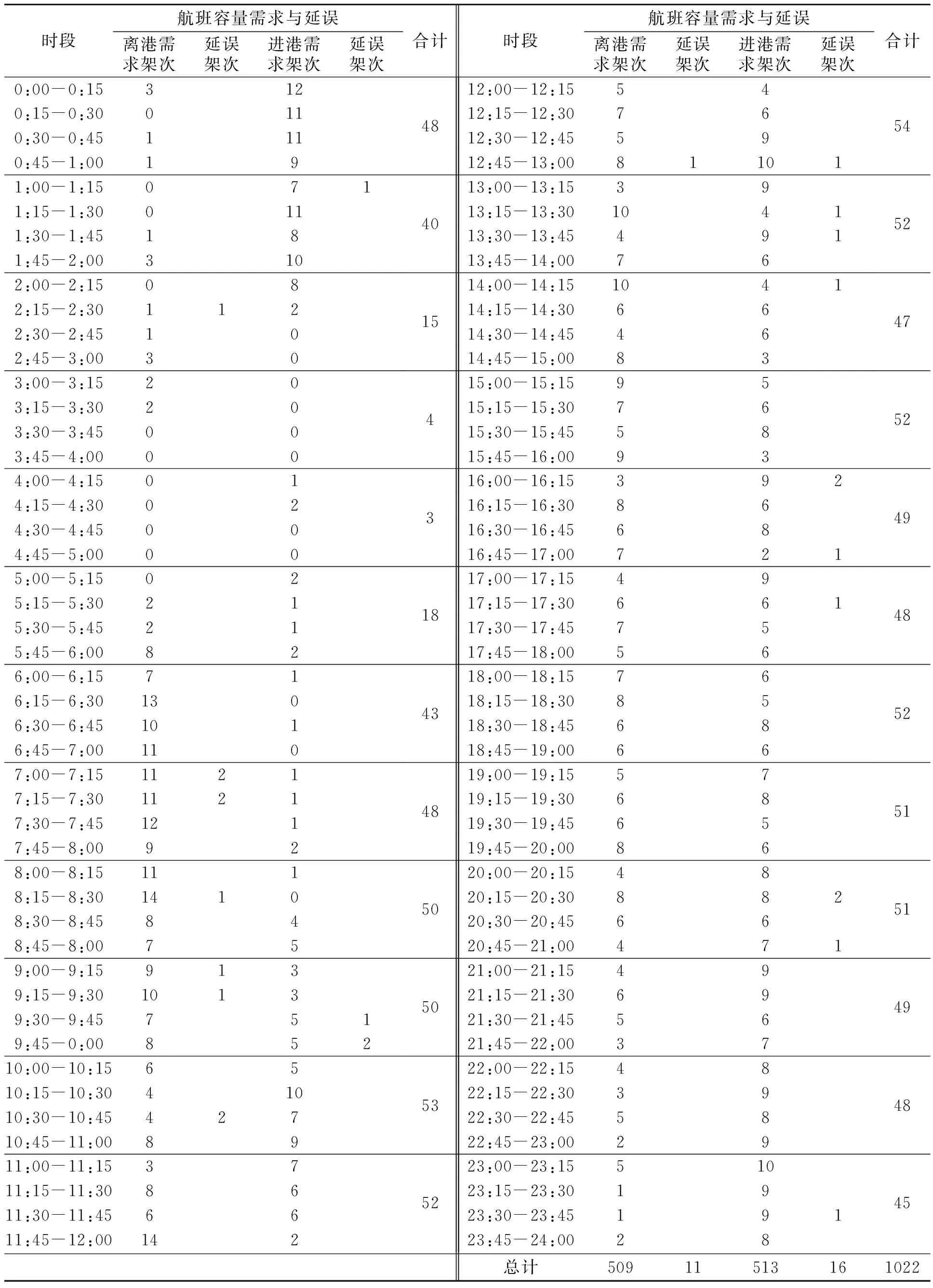
表1 双流机场进港和离港航班容量需求及运行数据Table 1 Capacity demands and operation data of arrival and departure flights of Shuangliu Airport

被取消的27架航班中有24架发生在进港和离港的高峰时段，即7:00-21:00。其中，进港航班被取消的时间区间在9:00-21:00，被取消14架；离港航班被取消的时间区间在7:00-13:00，被取消10架。航班被取消的原因与交通拥堵和延误有关，而交通拥堵和延误原因又与机场容量资源的估计和分配策略有关。

为了获得机场实际容量和极限容量，将表1中0:00-24:00各个时段的进港和离港航班架次需求分别投在直角坐标系中。横坐标表示各时段进港航班架次需求，纵坐标表示各时段离港航班架次需求。用线段合理地连接相关的数据点，由此构成机场容量曲线(图1)。机场容量曲线则由一组包络线段组成。由于机场容量曲线具有凸函数性质，这组包络线段其实就是一组函数不等式。这组函数不等式其实也就是限制机场进港与离港容量的约束条件。

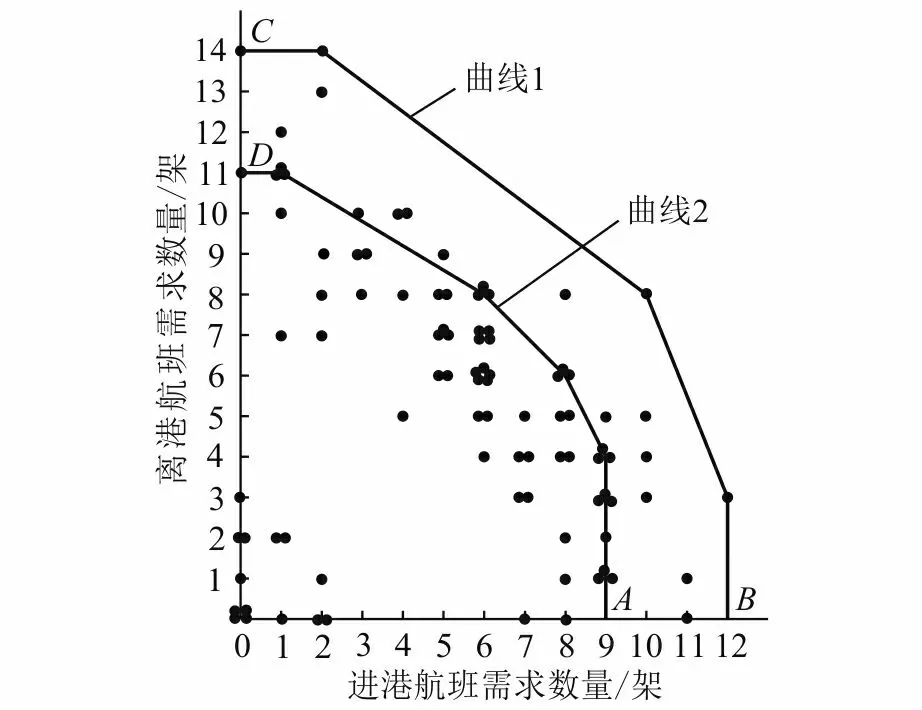
图1 机场进港和离港数据点分布和容量曲线Fig.1 Data point distribution and capacity curves of airport arrivals and departures

曲线1由进港和离港需求频率均为1的4个点和B、C连接而成的凸曲线，这5个数据点连接而成的凸曲线共同限制了其他所有的数据点。因此，这5个点都是极值点。该凸曲线即为机场的“极限容量”曲线。凸曲线顶点坐标分别是(0, 14)、(2, 14)、(10, 8)、(12, 3)、(12, 0)。其中，最大数值分别为12和14。这表明，按15 min计算，机场进港极限容量为12架，离港极限容量为14架,机场极限容量为26架进港和离港。如果同一时段实行降落和起飞混合运行，按15 min计算，机场极限容量为10架降落、8架起飞。机场最大极限容量为72架/h。

曲线2是由进港和离港需求频率均为3的6个数据点(包括A、D)连接而成的凸曲线。与曲线1相比较，可以清楚地看出曲线2非常稳健。因此，将其作为机场实际容量曲线是比较合理的。其特征如图2所示。

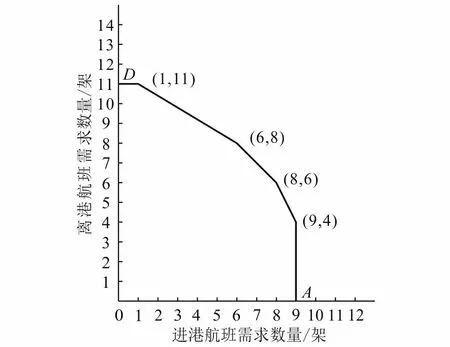
图2 机场容量曲线Fig.2 Airport capacity curve

从图2可看出，凸曲线上6个顶点坐标分别为(0, 11)、(1, 11)、(6, 8)、(8, 6)、(9, 4)、(9, 0)。其中，最大数值分别为9和11。这表明，按15 min计算，机场最大进港容量为9架，最大离港容量为11架，即最大容量为20架进港和离港。如果同一时段实行降落与起飞混合运行，按15 min计算，可以有14架起降，或者8架进港、6架离港，或者6架进港、8架离港。机场最大实际容量为56架/h。

2 机场容量与流量分配协同优化

2.1 进港和离港容量需求

为了解日常进港和离港容量需求情况，绘制了图3。从图3中可见，日常进港和离港容量需求高峰在07:00-24:00。进港和离港容量需求为45～54架/h，进港和离港容量需求平均为50.2架/h。

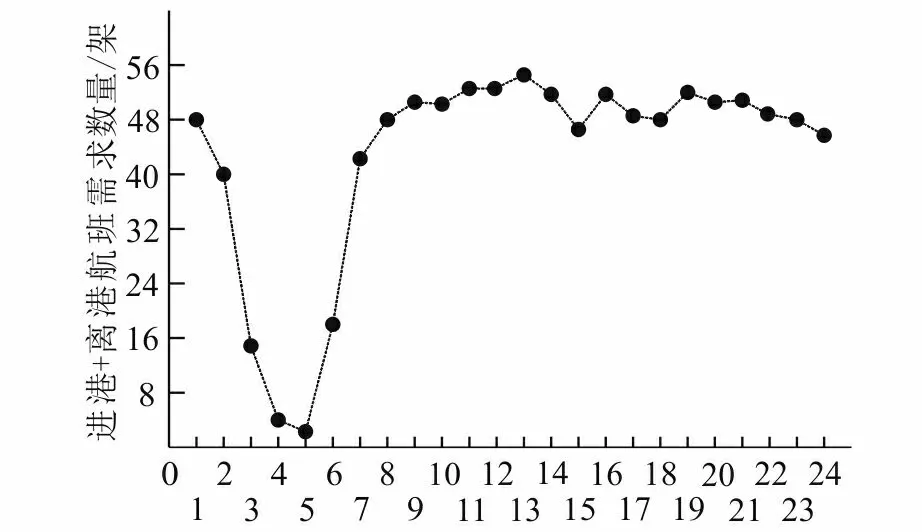
图3 0:00-24:00航班容量需求变化趋势Fig.3 Variation trend of flight capacity demand from 0:00 to 24:00 横坐标1表示0:00-1:00, 2表示1:00-2:00, 3表示2:00-3:00, ……

为了进一步了解从0:00-24:00进港和离港的容量需求变化情况，绘制了图4。

从图4中可看出，进港和离港航班的容量需求具有相反增长和下降特点：进港航班容量需求高峰在1:00-2:00之间，它的容量需求从高峰值43架/h降至0架/h，然后再逐渐增高到36架/h；离港航班需求高峰在7:00-9:00之间，其容量需求从5架/h降到0架/h，再增高到43架/h，然后逐渐降低到9架/h。在10:00-20:00时间区间，两者的容量需求都在20～30架/h。

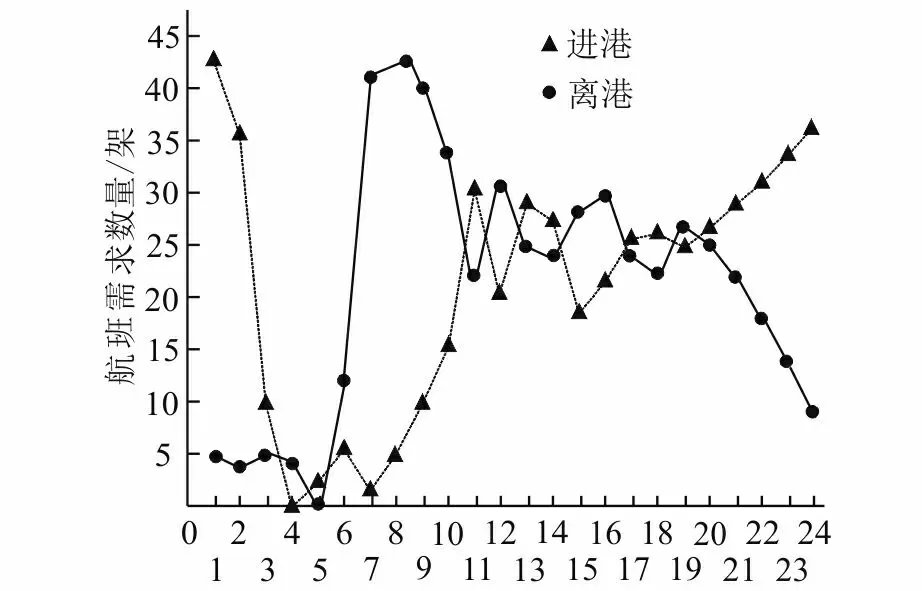
图4 0:00-24:00进港和离港容量需求变化Fig.4 The demand changes of arrival and departure capacity from 0:00 to 24:00 横坐标1表示0:00-1:00, 2表示1:00-2:00, 3表示2:00-3:00, ……

从两者容量需求特点可看出：机场航班起降在1:00-6:00时间区间内，机场航班起降趋势表现为进港航班容量需求大约是离港的11倍；在20:00以后，进港航班容量需求逐渐增高，而离港需求逐渐减少。两者的容量需求呈相反的增长和下降趋势。这种容量需求趋势意味着，机场和空管可以实行这样的战术管理：每天6:00以前，起飞航班多，2条跑道都用于起飞，其中1条跑道兼顾降落；在20:00以后，降落航班多，2条跑道用于降落，其中1条跑道兼顾起飞；7:00-20:00时间区间，使用隔离办法，1条跑道用于起飞，另1条跑道用于降落。这样可以最大限度减少由于机场和空管原因造成的拥堵和延误。

其次，更为重要的是，在10:00-20:00时间区间，起降航班容量需求平均高达50.2架/h，很容易发生拥堵和延误。因此，实施进港和离港容量需求协同优化具有必要性。

2.2 容量与流量协同优化模型

机场容量优化问题其实就是整数线性规划问题。据此，在不考虑定位点容量限制情况下，优化问题的目标函数表达如下

(1)

式中：ui为第i(i∈I)个时隙机场最大进港容量；vi为第i(i∈I)个时隙机场最大离港容量；i={1,2,…,N},表示长度为15 min的一组时隙；N为时隙个数；a为优先级参数，0≤a≤1。在式中，优先级参数起着对进港和离港航班需求偏好作用。当a=0.5时，表示进港和离港航班同等优先，如果a=0.7时，表示对进港航班偏好。

0≤ui≤9， (i=1，2，…，N+1)

(2)

0≤vi≤11， (i=1，2，…，N+1)

(3)

vi+0.6ui≤11.6，(i=1，2，…，N+1)

(4)

vi+ui≤14，(i=1，2，…，N+1)

(5)

vi+2ui≤22，(i=1，2，…，N+1)

(6)

由约束条件围成的可行域即为机场实际容量值域范围。

（1）供电企业的相关工作人员要适应现代企业发展和建设的趋势，加强企业职工的竞争观念和开放意识，充分认识到在经济新常态背景下，供电企业所面临的挑战，产生危机感、紧迫感和使命感，从而主动的规范和约束自身行为，为增强企业经济利益和提升社会效益贡献一份力。

在获得机场进港和离港实际容量的基础上，选择交通繁忙、最容易发生拥堵和航班延误的10:00-12:00时间区间，进一步研究进港和离港容量的协同优化问题。按15 min划分为8个时段，8组进港和离港航班容量需求如表2。

在2 h内，进港和离港航班容量总需求为105架。其中，降落需求52架，起飞需求53架。但是，依照机场每15 min的实际容量，可见在2个时段内总共有4架进离港需求超过了机场实际容量(图5)，延误不可避免。其中在10:15-10:30，有1架进港航班延误；在11:45-12:00，有3架离港航班延误。

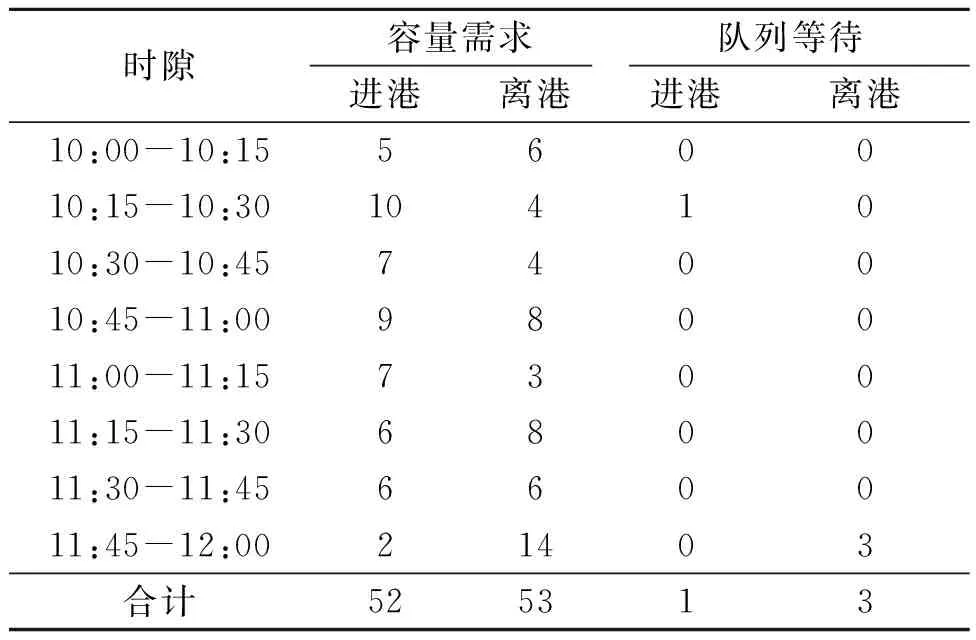
表2 初始容量需求及延误Table 2 Initial capacity requirements and delays

图5 初始容量需求分布Fig.5 Distribution of initial capacity demands

为了实现供需平衡，规避航班延误风险，对运用整数线性规划建立的数学模型(1)式，采用Matlab执行遗传算法对模型求最优解，以实现机场实际容量最大化。算法程序运行参数设置如下：

初始种群规模：100；

最大世代数：120；

选择率：0.2；

交叉率：0.7；

变异率：0.1。

输入参数：各时段进港和离港容量需求累计

ui=[5, 15, 22, 31, 38, 44, 50, 52](进港需求累计)；

vi=[6, 10, 14, 22, 25, 33, 39, 53](离港需求累计)。

容量曲线约束条件：

0≤ui≤9；

0≤vi≤11；

vi+0.6ui≤11.6；

vi+ui≤14；

vi+2ui≤22。

根据进港和离港容量需求，将优先级参数设定为a=0.5，即进港和离港航班同等优先。

从表3、图6和图7中可以看出，所有进港和离港容量需求都满足了机场容量约束条件。在进港和离港容量需求不变的情况下，经容量协同优化，进港和离港容量需求被重新分配，平衡了供需，合理规避了拥堵和延误风险。相较而言，在a=0.5的情况下，对离港需求有利，在11:45-12:00时段，有10个航班离港，只有2个航班进港。当a=0.7时，也就是把进港优先级提高了0.2的情况下，最优策略偏向于进港航班，缩小了各时段进港与离港航班容量需求差距。

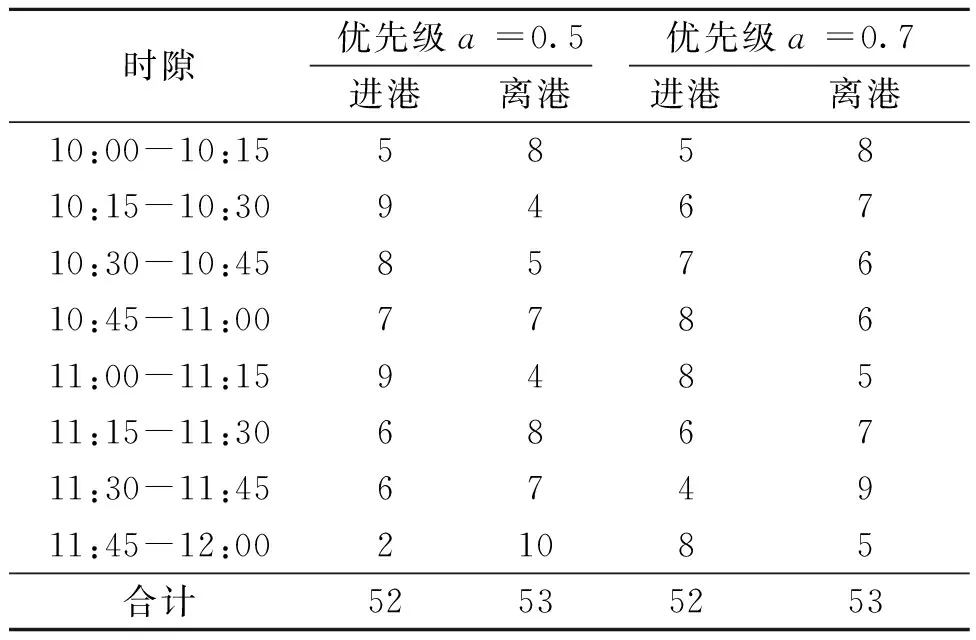
表3 进港和离港容量需求协同优化结果Table 3 Results of collaborative optimization of arrival and departure capacity demand

图6 优先级a=0.5航班容量需求分布Fig.6 Distribution of flight capacity demands with priority a=0.5

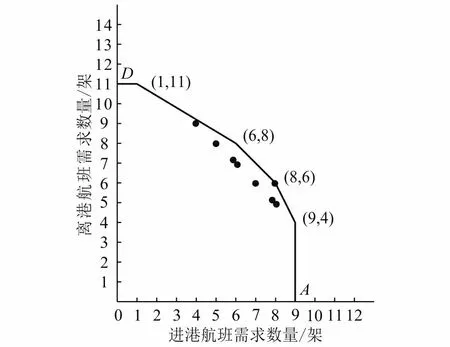
图7 优先级a=0.7航班容量需求分布Fig.7 Distribution of flight capacity demands with priority a=0.7

表4展示了初始航班容量需求与优化后各时段航班容量需求的对比结果。

表4 优化前后各时段容量需求(进港+离港)对比Table 4 Comparison of capacity demand in each period before and after optimization

从对比结果可见，各时段初始航班需求级差为7架(17-10=7)。当优先级设置为a=0.5，对初始航班容量需求优化后，其航班需求级差减少为2架(14-12=2)。当优先级设置为a=0.7，对其优化后，航班需求级差仅为1架(14-13=1)，最大限度缩小了各时段航班需求级差。

2.3 验证

为验证该方法的有效性和可行性，选择12:00-14:00时段机场进港和离港航班高峰时段进行分析。表5列出了该时段进港和离港的容量需求。

在这2 h内，进港和离港航班容量总需求为106架。其中进港需求57架，离港需求49架。根据机场每15 min的实际容量判断，有6架进离港容量需求超过了机场实际容量，则延误将会发生(图8)。

表5 初始容量需求及延误Table 5 Initial capacity demands and delays

图8 容量需求分布Fig.8 Capacity demand distribution

按照前述算法对初始容量需求进行协同优化，分别将优先级系数设定为a=0.5和a=0.7进行运算，结果见表6、表7、图9和图10。

从结果看出，各时段进港和离港航班容量需求得到了优化平衡，验证了本方法的有效性和可靠性。其余时段航班需求采用本方法进行优化，可收到相同效果。有效避免交通拥堵和航班延误的同时，也兼顾了各航空公司的利益，极大地减轻了空管和机场的运行管理难度。本方法和技术适用于同类大型繁忙机场。

表6 进港和离港容量需求协同优化结果Table 6 Collaborative optimization results of arrival and departure capacity demands

表7 优化前后各时段容量需求(进港+离港)对比Table 7 Comparison of capacity demand in each period before and after optimization

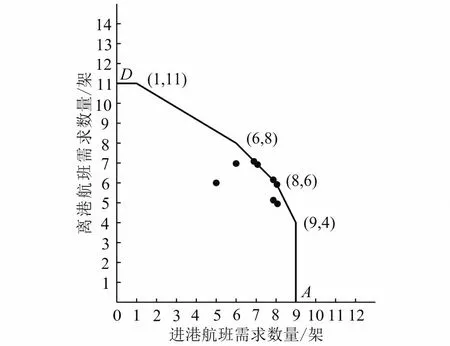
图9 优先级a=0.5航班容量需求分布Fig.9 Distribution of flight capacity demand with priority a=0.5

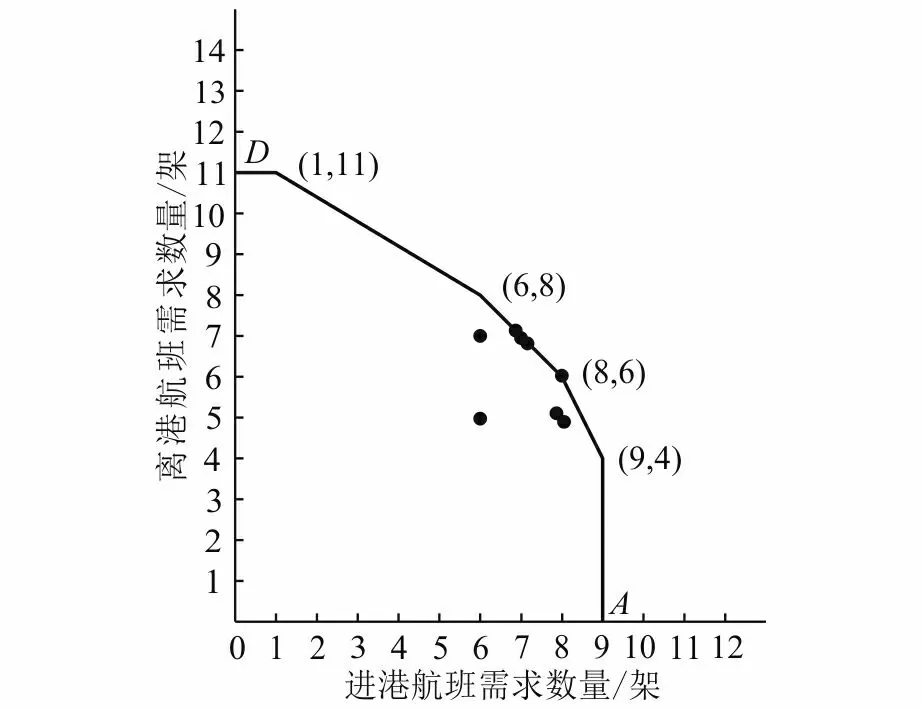
图10 优先级a=0.7航班容量需求分布Fig.10 Distribution of flight capacity demand with priority a=0.7

3 结 论

通过以上研究，得出如下结论：

a.采用包络线可行域估算机场实际容量和极限容量具有可行性和可靠性。成都双流国际机场最大极限容量为72架/h，最大实际容量为56/h。所获得的容量数据是真实可靠的，可以作为机场制定战略交通管理方案和机场容量资源分配策略的参考依据。

b.相对于使用人工蜂群算法的渐进二元启发式方法[17]及自适应大邻域搜索等算法[15]而言，应用遗传算法对模型求最优解具有先进性，对机场容量最大化具有有效性。实例证明和验证结果表明，在单位时段内，超过机场实际容量的进港和离港航班在采用本方法优化后，不仅避免了拥堵和延误，各时段进港和离港航班容量需求也更加平衡。并且，该方法可做到在不扩大机场容量的前提下，利用现有的容量资源满足交通需求，最大程度提高了机场容量资源利用率。

c.根据成都双流机场全日各时间区间进港和离港容量需求具有相反增减特点，机场和空管在有效实施战略交通管控的同时，可以更加合理地分配双跑道容量资源：每日6:00以前，实行双降落兼顾起飞；20:00以后，实行双起飞兼顾降落；7:00-20:00时间区间实行起降隔离，一条跑道用于降落，另一条跑道用于起飞。这样的运行方式既可保证最大限度减少时隙浪费，也有利于降低空中交通拥堵和航班延误。