光伏并网逆变器LCL滤波器参数设计方法
孔令霞,王维庆,王海云
(新疆大学电气工程学院,新疆 乌鲁木齐市 830047)
1 引言
随着化石能源的短缺,太阳能和风能等可再生能源的利用得到了广泛关注[1],而以光伏发电为代表的发电方式是清洁能源发电的重要组成部分。在新能源发电并网系统中,滤波器是连接并网逆变器和电网的重要元件。LCL滤波器因其滤波性能好,开关损耗小,成本低,体积小等优点而被广泛应用于光伏并网逆变系统[2-4]。LCL滤波器参数设计合理与否,直接影响滤波效果、滤波器体积和电网的稳定性。新能源并网逆变系统对并网点处的入网电流有严格的并网标准,故LCL滤波器参数设计是否有效可依据并网点处的入网电流是否满足并网要求来判断[5]。其中并网点处电流总谐波畸变率(total harmonic distortion,THD)是衡量并网电流是否满足并网要求的重要指标[6-7]。而LCL滤波器的参数设计过程比较复杂,这也使得其参数设计成为研究热点[8]。
为了节约LCL滤波器的成本,减小其体积,文献[9]所提的LCL滤波器参数设计方法通过分析逆变器侧谐波产生的原因,计算各次谐波,并建立THD估算模型,期望以并网电流的谐波畸变率为目标设计滤波器各参数值,该方法没有严密的数学推导,且多依赖于经验,对实际工程中LCL光伏并网滤波器的设计可借鉴性不强。文献[10]所提方法从LCL滤波器逆变器侧电流纹波产生机理出发,推导出逆变器侧电感计算公式,再根据入网电流质量要求的各次谐波的限制指标以及网侧电感和电容器储能最小为目标,确定网侧电感和滤波电容的参数值,然后通过硬性约束条件反复校验和修正才能得到理想的各参数值。该方法复杂,在实际工程中不便实现。文献[11]中的方法通过电流纹波衰减率来计算网侧电感值,并通过无功吸收比来设计滤波电容。虽然对于各参数设计来说,该方法有严密的数学公式推导,但没有考虑LCL滤波器总电感压降约束条件,使得设计的滤波器总电感压降较大,影响并网系统电压质量。文献[12-13]提出了一种图解法来设计LCL滤波器各参数,此方法能直观反应各参数之间的相互关系,从而确定滤波器各参数值。该方法局限在于,若某一参数变化,其它参数相应变化,故增加了滤波器设计的复杂程度,且该方法没考虑各种优化目标,所以其设计结果不一定最优。文献[14]提出一种基于遗传算法的LCL滤波器参数优化方法,其优化目标包含了纹波电流最小化、功率损耗最小化和谐波衰减最大化,但并没有考虑总电感值最小化,电感比例系数最小化等优化目标,故具有一定局限性。
对于上述LCL滤波器设计方法存在的不足,同时为保证并网电流满足要求且LCL滤波器满足多个优化目标,在传统图解法的基础上,提出一种LCL滤波器参数设计方法。所提方法从LCL滤波器逆变器侧电流、网侧电流与逆变器侧电压的传递函数的伯德图为切入点,分析其滤波性能,然后分析逆变器侧电流、网侧电流与电感比例系数及电容的关系,再根据LCL滤波器设计要求、电网硬性约束条件,确定各参数的大致范围。最后以纹波电流小、谐波衰减性能好、总电感值小、阻尼电阻功率损耗小和电感比例系数小为目标设计目标函数,通过灰狼算法确定各滤波器参数最优值,并在Matlab仿真平台搭建仿真模型,验证所提设计方法的有效性。
2 光伏并网逆变系统分析
2.1 三相光伏并网逆变系统电路拓扑结构
采用LCL型并网滤波器的三相光伏并网逆变系统主电路拓扑结构如图1所示。

图1 三相光伏并网系统拓扑图
图中PV为光伏阵列,C为直流稳压电容,S1-S6为6个IGBT晶体管开关,VD1-VD6为续流二极管,R1是逆变器侧电感L1的内阻和开关管损耗的等效电阻,R2是逆变器侧电感L2的等效内阻,Cf是滤波电容,Rd为滤波电容支路阻尼电阻,Udc为稳压电容端电压,Us为电网电压。
2.2 LCL滤波器特性分析
2.2.1LCL滤波器数学模型
并网逆变器侧输出电压由基波电压和谐波电压两部分组成。R1和R2很小可忽略,故LCL滤波器在并网模式下的谐波电源等效数学模型如图2所示。
图2 LCL滤波器并网模式下谐波等效模型
上图中,Uh为谐波电压源电压,i1是逆变器侧输出电流,i2是网侧电流,Us为电网电压。则可得i1与Uh的传递函数,如式(1)所示
(1)
利用Matlab绘制出有阻尼型LCL滤波器、L1型和L1+L2型滤波器传递函数Y11(s)的Bode图,如图3所示。
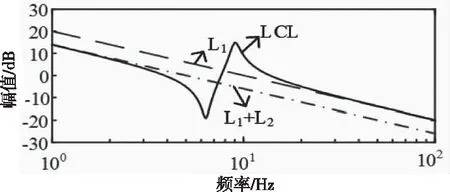
图3 滤波器Y11(s)伯德图
由上图可知,对逆变器侧电流i1来说,在低于谐振频率时,LCL型滤波器的滤波效果和单L1+L2型滤波器相近,而在高于谐振频率时,LCL型滤波器的滤波效果和单L1型滤波器相近。
2.2.2 逆变器侧电流与电感比例系数和滤波电容关系
将s=jhω带入式(1)(h为谐波次数,ω为电网基波角频率)可得LCL型滤波器逆变器侧电流i1与Uh的幅值关系,如式(2)所示
(2)
式中:A(jhω)和B(jhω)分别如式(3)和(4)所示
A(jhω)=1-h2ω2L2Cf+jhωRdCf
(3)
B(jhω)=h2ω2RdCf(L1+L2)-jhω(L1+L2)+h3ω3L1L2Cf
(4)
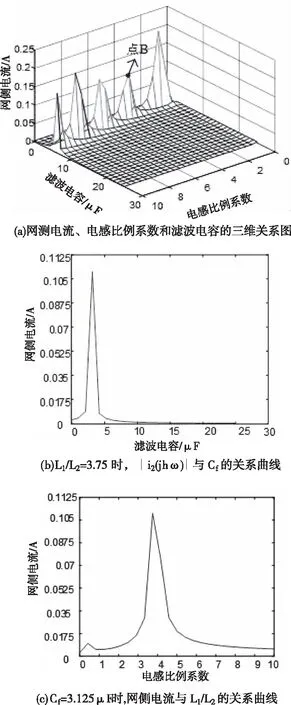
假设开关频率fsw为10kHz,取开关频率处(即h=200)谐波电压源,可得逆变器侧电流∣i1(jhω)∣、电感比例系数L1/L2和滤波电容Cf的三维坐标关系图,如图4(a)所示。从图中可以看出,A点附近的谐波电流、电感比例系数和电容取值都比较小。A点坐标为(3.75,3.125,0.1875),取L1/L2=3.75,可得∣i1(jhω)∣与Cf的关系曲线,如图4(b)所示。再取Cf=3.125μF,可得逆变器侧电流与L1/L2的关系曲线,如图4(c)所示。
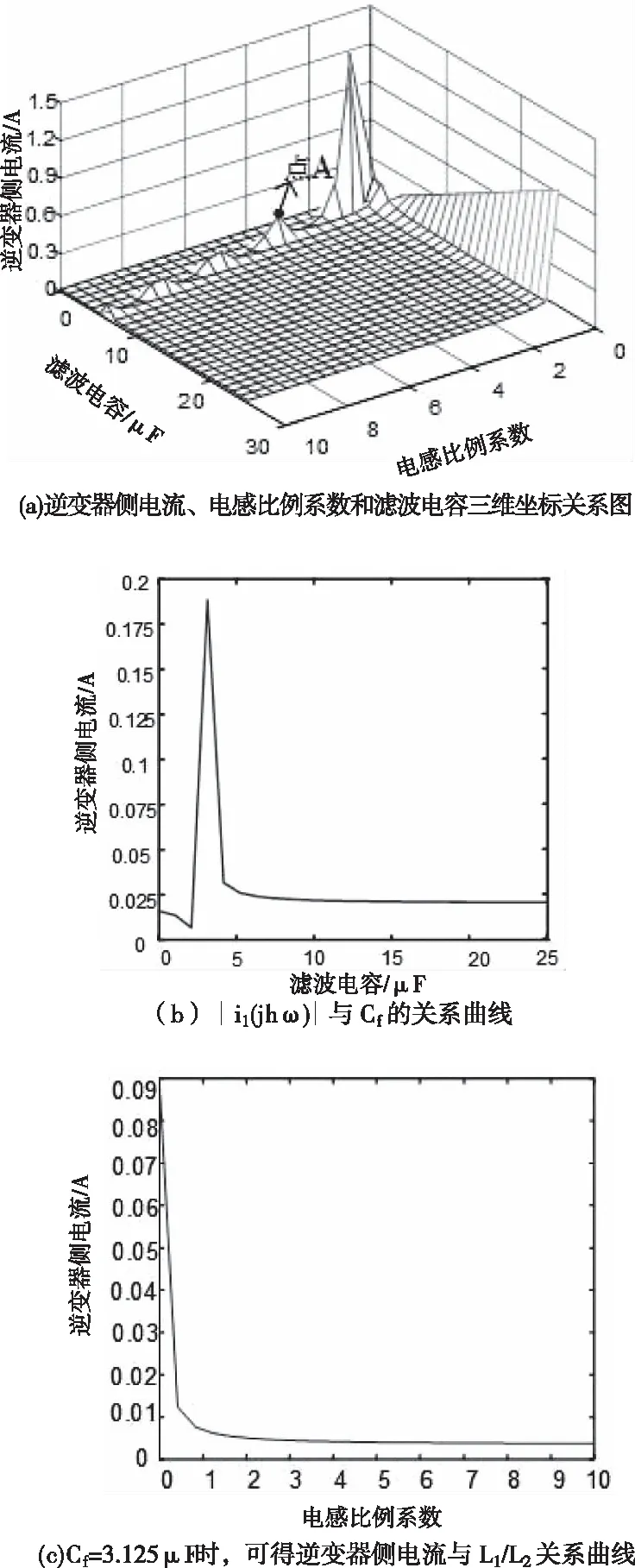
图4 逆变器侧电流幅值与L1/L2和Cf关系图
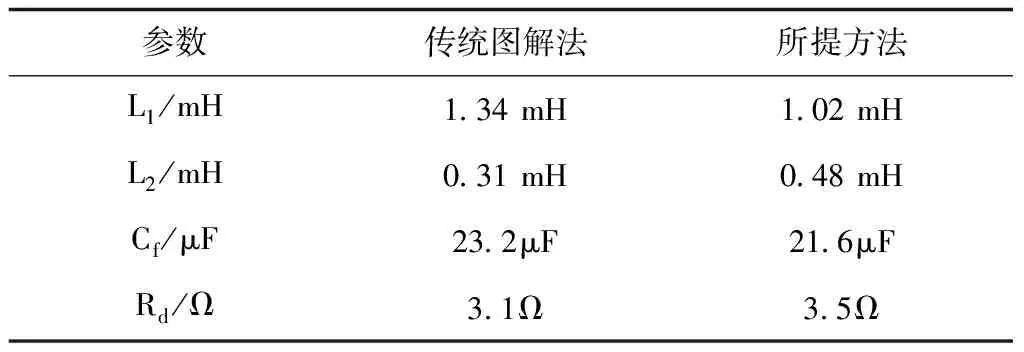
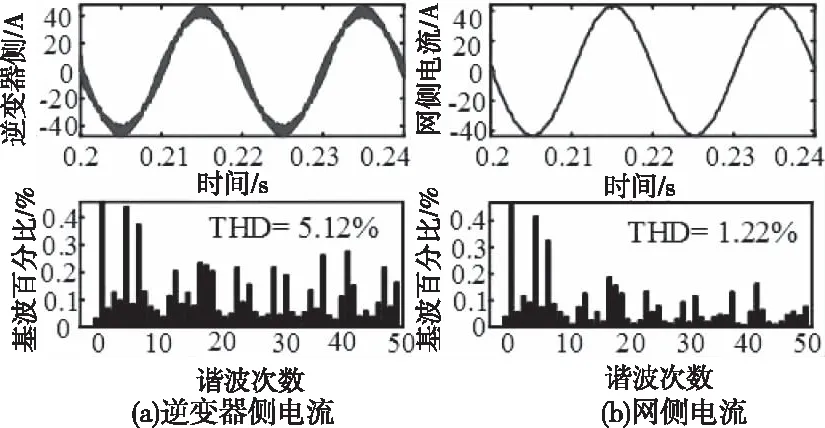
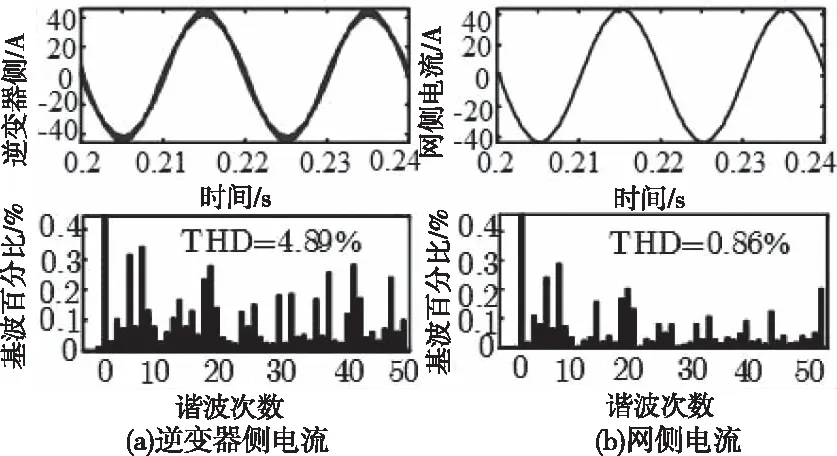
由图4(b)可知,电感比例系数一定的情况下,纹波电流的幅值与电容的关系曲线是一条线在0 2.2.3 网侧电流与电感比例系数及电容关系 由图2可得有阻尼型LCL滤波器网侧电流i2和逆变器侧电压Uh之间的传递函数,如式(5)所示 (5) 对于L1+L2型滤波器来说,其网侧电流和逆变器侧电压之间的传递函数如式(6)所示 (6) 利用Matlab绘制出L1+L2型滤波器、有阻尼和无阻尼型LCL滤波器传递函数Y21(s)的Bode图,如图5所示。 图5 滤波器Y21(s)伯德图 由上图可知,对于网测电流i2来说,在低于谐振频率时,LCL型滤波器和L1+L2型滤波器的滤波效果相近,而高于谐振频率时,LCL型滤波器幅频衰减特性斜率明显优于L1+L2型滤波器。而相较于无阻尼LCL型滤波器,有阻尼型LCL滤波器有效抑制了谐振峰。 将s=jhω带入式(3),可得有阻尼型LCL滤波器网侧电流和逆变器侧电压的幅值关系,如式(7)所示 (7) 式中:C(jhω)如式(8)所示,B(jhω)如式(4)所示 C(jhω)=1+jhωRdCf (8) 由此可画出网测电流∣i2(jhω)∣、电感比例系数L1/L2和滤波电容Cf的三维关系图,如图6(a)所示。从图6(a)可看出,相比于图4(a),经LCL滤波器后,谐波电流幅值有明显减小。图6(a)中B点是图4(a)中点A的对应点,其坐标为(3.75,3.125,0.1085)。取L1/L2=3.75,可得∣i2(jhω)∣与Cf的关系曲线,如图6(b)所示。再取Cf=3.125μF,可得网侧电流与L1/L2的关系曲线,如图6(c)所示。 图6 网测电流幅值与L1/L2和Cf关系图 图6(b)与图4(b)的变化趋势及其变化原理一致,这里不再赘述。由图6(c)可知,在滤波电容一定的条件下,网测谐波电流幅值与L1/L2的关系图是一条先缓慢增加,再急剧增加,然后急剧下降,最后趋于平稳的曲线。即当电感比例系数在4附近时,谐振频率与开关频率重合。故在满足滤波效果的情况下,电感比例系数应在合适范围内取值。 LCL滤波器各参数的设计应结合系统参数,综合考虑各方面的因素,才能使设计的LCL滤波器参数有效可行。综合文献[9-14],LCL滤波器参数设计应满足以下约束条件。 3.1.1 总电感值约束条件 对于LCL滤波器来说,总电感值越大,其滤波效果越好,但是滤波器的体积也越大,成本也越高,对系统的动态响应影响也越大。综合考虑以上因素,可根据总电感压降约束条件确定总电感值的上限,如式(9)所示。 (9) 其中Us为电网线电压有效值,P为逆变器输出有功功率,ω是电网角频率。 3.1.2 逆变器侧电感L1下限约束条件 随着L1的增加,滤波器的成本呈指数增长。所以在满足并网电流要求的情况下,逆变器侧电感L1越小越好。而最大允许纹波电流对电感L1的造价和重量影响很大,过大的电流纹波会增加功率模块的容量,这意味着损耗、温升和电感L1成本和体积的增加。所以在设计L1时应考虑纹波电流的影响。所提方法采用三电平SPWM调制方式,纹波电流计算公式如式(10)所示 (10) 其中,Ts是开关周期,Udc是稳压电容端电压,M是调制比。通过式(14)找出最大纹波电流Δimax,则电感L1的下限可由式(11)确定,其公式如下 (11) 其中fsw为开关频率。 3.1.3 谐振频率约束条件 LCL滤波器参数设计时,谐振频率的选择以满足谐波衰减的需求为主,为了提高对高次谐波(开关及其倍频次谐波)和低次谐波的抑制效果,谐振频率应低于最小的主导低频边带谐波,故对LCL滤波器的谐振频率fres有如下要求 (12) 式中,f1是电网基波频率。 3.1.4 滤波电容约束条件 滤波电容Cf越大,从滤波电容支路流过的高频谐波分量越多,但滤波电容过大,其吸收的无功功率越多,会降低电网的功率因数。故为了保证并网系统的高功率因数,滤波电容Cf吸收的无功功率不应高于系统额定功率的5%,其约束条件如式(13)所示 (13) 其中,P为系统额定输出有功,Em为相电压有效值。 传统图解法所设计的LCL滤波器参数只考虑了滤波效果,没有综合考虑相应的优化目标,故具有一定局限性。而所提方法在传统图解法的基础上考虑了五个优化目标,即纹波电流最小化、谐波衰减最大化、总电感值最小化、功率损耗最小化、电感比例系数最小化,并建立如下目标函数。 minf(x)=ω1f1+ω2f2+ω3f3+ω4f4+ω5f5 (14) 其中子目标函数minf1表示最小纹波电流,如式(15)所示;minf2表示最小纹波衰减比值λ,如式(16)所示;minf3表示LCL滤波器总电感值之和LT=L1+L2最小;minf4表示功率损耗Ploss最小,如式(17)所示(ω为电网基波角频率,Ui为逆变器输出电压);minf5表示电感比例系数L1/L2最小。 (15) (16) (17) 依据熵值权重法[14]可确定每个子目标的权重系数ωi,将其带入式(14)则可得线性加权后的目标函数,如式(18)所示: minf(x)=0.1660△imax+0.1757λ+ (18) 其中λ为谐波衰减比值,如式(11)所示。 灰狼算法因其结构简单、控制参数少、易于操作和全局搜索能力强等特点被广泛应用于参数优化领域,故本文用灰狼算法确定LCL滤波器各参数值。 在灰狼算法中,通过式(19)确定各组狼与猎物(最优解)的距离,在根据式(20)更新狼群位置 D=|C*Xp(t)-X(t)| (19) X(t+1)=Xp(t)-A*D (20) 其中,D代表第t次迭代时灰狼个体与猎物的距离,Xp(t)表示第t次迭代时猎物的位置,X(t)表示第t次迭代时灰狼个体的位置,C为摆动因子,A为收敛因子。 狼群中的普通狼(ω狼)根据式(21)确定自己与前三名α、β和δ狼的距离,然后通过式(22)更新各自的位置,最后根据式(23)对猎物进行定位,判断出个体向猎物移动的方向,再由α狼带领β、δ和ω狼逐渐向猎物靠近并包围猎物。灰狼算法的流程图如图(7)所示。 图7 灰狼算法流程图 (21) (22) Xp(t+1)=(X1+X2+X3)/3 (23) S1)设置变量X=[L1,L2,Cf,Rd],根据滤波器设计要求和约束条件,确定各参数取值上下界。取狼群的大小为N、最大迭代次数为M,并初始化灰狼种群。 S2)根据求解目标计算每只狼的适应度值,并选择排名前三的狼个体依次赋予Xα、Xβ和Xδ。 S3)由Xα、Xβ和Xδ,通过狼群包围和狼群捕猎的步骤,可根据式(21)可计算出其它灰狼与α、β和δ狼之间的距离。 S4)根据式(22)和式(23)向占据最优位置的成员移动,优化狼群中每只狼的位置。 S5)在更新后的α、β和δ狼中,把适应度最高的灰狼与目标函数做对比,然后进行位置更新和目标函数更新,确定最优解。 S6)判断迭代次数是否达到预设最大迭代次数,达到最大迭代次数则输出最优解,否则转步骤S2。 为提高算法精确,得到最优解,取灰狼种群规模为N=100,最大迭代次数M=200,根据图4、图6和式(17)给各参数变量赋合适初值。 为说明所提方法的优越性,给出同样条件下传统图解法设计的LCL滤波器参数和所提方法设计的LCL滤波器参数,如表(1)所示。 为验证所LCL滤波器参数设计方法的可靠性和优越性,按两种方案所设计的LCL滤波器参数值(见表1)分别在Matlab/simulink平台搭建光伏并网逆变系统仿真模型。并网逆变系统参数设置如下:系统额定功率为15kW,交流线电压有效值为380V,直流电压为700V,电网频率为50Hz,逆变器开关频率为10kHz。 表1 两种方案下的参数设计结果 传统图解法设计的LCL滤波器对应的逆变器侧电流i1和网测电流i2波形及其对应频谱图如图8(a)、(b)所示。本文所提方法设计的LCL滤波器对应的逆变器侧电流i1和网侧电流i2波形及其对应频谱图如图9(a)、(b)所示。 图8 传统图解法A相电流波形及其频谱分析 图9 所提设计方法A相电流波形及其频谱分析 由图8和图9可知,采用传统图解法设计的LCL滤波器时,并网逆变器侧电流TDH=5.12%,网侧电流TDH=1.22%,经滤波器滤波,谐波TDH降低了3.9%。而采用所提方法设计的LCL滤波器时,并网逆变器侧电流TDH=4.89%,网侧电流TDH=0.86%,谐波TDH降低了4.03%。 对两者进行对比可知,用文中方法设计的LCL滤波器的谐波衰减性能优于用传统图解法设计的LCL滤波器,且采用所提方法设计的LCL滤波器的并网系统的电流质量更好。 通过对并网逆变系统LCL滤波器的传递函数进行分析,根据滤波器设计要求采用灰狼算法对滤波器参数进行优化,把参数设计结果和光伏并网逆变系统仿真结果进行对比,可得出如下结论: 1)与传统图解法相比,所提LCL滤波器参数设计方法的总电感值更小,且逆变器侧电感和滤波电容也更小,但阻尼电阻略大,总体说来所提设计方法设计的滤波器成本更低。 2)仿真结果表明,提出的LCL滤波器设计方法的TDH下降更显著,其谐波衰减性能优于用传统图解法设计的LCL滤波器。 3)相比于传统图解法,采用所提方法设计的LCL滤波器的逆变器侧和网侧的谐波电流更小,意味着其温升和损耗也更小,并网电流质量更高。 总体说来,所提方法设计的光伏并网LCL滤波器滤波效果良好且较为经济,说明此参数设计方法有效可行,对实际工程中LCL型光伏并网滤波器的设计有可借鉴性。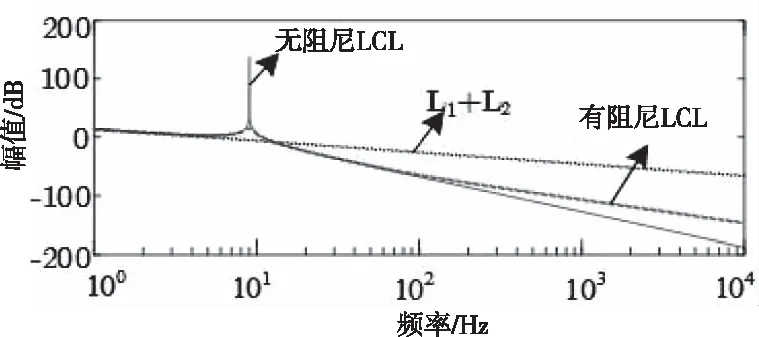
3 LCL型滤波器的参数优化设计
3.1 LCL滤波器参数设计约束条件
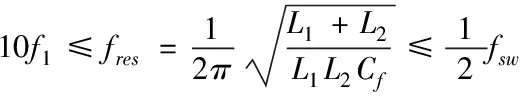
3.2 优化目标
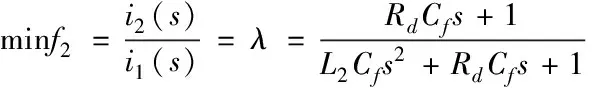
4 LCL滤波器参数灰狼算法优化方法
4.1 目标函数
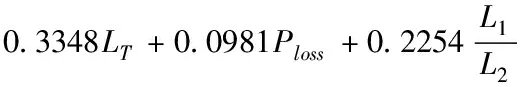
4.2 灰狼算法优化过程
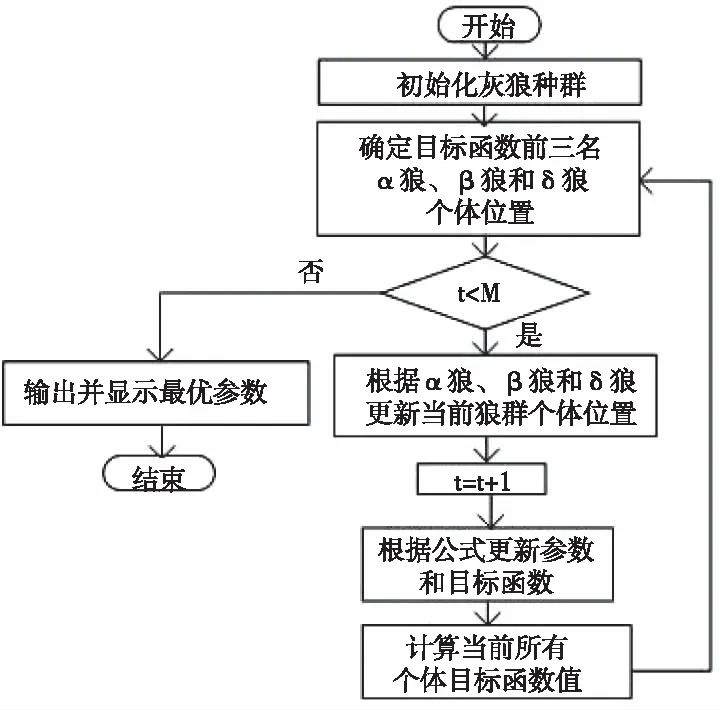
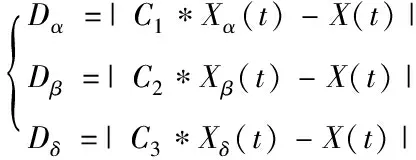
4.3 算法优化结果
5 仿真及结果分析
6 结论

