主动声纳的时频盲分离算法研究

杨 阳，张 诚，丁元明

(1. 大连大学通信与网络重点实验室，辽宁 大连 116622；2. 大连大学信息工程学院，辽宁 大连116622)

1 引言

浅海主动声纳发射声波探测水下目标，感兴趣的目标物体声散射形成目标回波，其包含目标的属性信息[1]。海洋界面及水中散射体散射形成混响，散射体与沉积层的不均匀性使得混响的统计分布具有随机的特点。盲源分离方法[2]是在缺少信源及信道先验知识的条件下，仅利用接收数据恢复出感兴趣源的技术。越来越多的研究人员根据目标回波与混响统计特征差异，设计盲分离算法应用于主动方式目标探测[3-5]。文献[6-7]利用主元素逆PCI算法抗混响，根据目标回波和混响的能量差异，对接收信号做奇异值分解，通过秩的选取提取目标回波。该方法在合理的混响模型假设下能够有效抑制混响，但分离性能受信号秩估计准确性影响严重，实际水声环境复杂，增大了对秩的准确估计难度。在此基础上，文献[8]利用有无目标回波信号时数据的奇异值差异抗混响。给出无目标参考波束和目标回波波束估计混响秩的方法，提高了混响秩估计的准确性。但在实际测量中，波束宽度是随着方位角而变化的，且波束宽度是有限的，因而，很难判断参考波束中是否包含完整的目标回波信息，可能损失目标信息。本文研究主动声纳目标亮点信号的时频盲分离方法，推导目标亮点与混响的魏格纳-威尔(WVD)表达式，分析主动声纳回波信号的时频分布特征差异，研究建立利用信号时频特征的分离算法和优化算法，该方法不需要预估声纳信号的能量秩，通过结合形态滤波能够有效抑制混响和交叉项干扰，准确提取目标亮点的自项时频信息，进而提高算法的分离准确性。

2 主动声纳回波信号的时频特性分析

主动声纳发射声波探测目标，第k个基元接收信号的数学模型可表示为

xk(t)=hk(t)*s(t)+n(t)

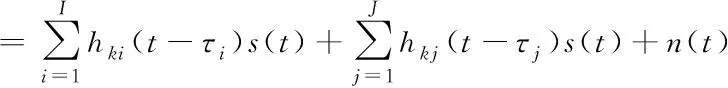
(1)

式中，s(t)是发射信号，hki(t)、hkj(t)分别代表目标第i个散射单元、界面第m×1个散射单元与基元k间的信道冲激响应，接收信号包含目标回波、混响和海洋噪声n(t)。式(1)可改成矩阵形式[9]

x(t)=As(t)+n(t)=xT(t)+r(t)+n(t)

(2)

其中，A称作混合矩阵，反映水下声信道的传输特性。xT(t)=∑hki(t-τi)s(t)是目标回波，r(t)=∑hkj(t-τj)s(t)是混响。

发射线性调频信号(LFM)s(t)=K·exp(j2π(f0t+kt2/2))，斜率k=(f1-f0)/T，时间t=[-T/2，T/2]，计算目标回波信号的WVD分布

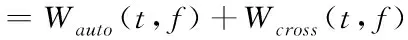
(3)

式中，Wxi，i=1，2…I是目标亮点自项分布，记为Wauto(t，f)。Wxij，i≠j，i，j=1，2…I是目标亮点间互项(也成交叉项)分布，记为Wcross(t，f)。将发射信号形式带入式(3)，计算目标亮点自项的WVD分布得

=|I2e2jπ(f0+kt-f)T(T-2|t|)sin c[2π(f0+kt-f)(T-2|t|)]|

=I2(T-2|t|)sin c[2π(f0+kt-f)(T-2|t|)]

(4)

计算目标亮点间的互相WVD分布得

Wcross(t，f)=WVDR12(t，f)+WVDR21(t，f)

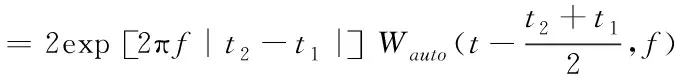
(5)

式(4)、(5)表明，单目标亮点的WVD是一组斜率为k的sinc函数，近似为时频图上的一条连续斜线；目标亮点间互相是自项分布与指数项exp(j2πfτ)的成积，表现为时频图上的一条断续斜线，其能量是自项的2倍，且位于相应的自项间。

混响是主动声纳发射信号时，界面、水体中散射体等散射信号的叠加，具有相位随机性。单个散射元的自项WVD为

Wr(t，f)=K2(t)Ws(t-τi，f)

(6)

第m、n散射单元间的互项WVD为

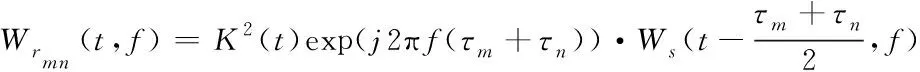
(7)

其中，K(t)是t时刻某一散射单元的散射幅度，τ是某一散射单元相对发射信号的时间延迟，Ws(t)是发射信号的WVD分布。可以看出，各散射单元的自项和互项WVD时频分布均是由幅度、时移随机的Ws(t)构成的，因此，大量随机散射单元混合形成的混响WVD图像可能不再具有线状特征。图1是利用亮点模型[4]仿真的三分量目标信号WVD时频分布，三个连续亮点间存在间断的互项谱线。图2是仿真混响的WVD，其时频图像是随机的点或块分布，不再是与发射信号同斜率的连续线谱，仿真和与理论结果一致。

图1 三分量目标亮点WVD分布

图2 混响WVD分布

3 基于信号时频特征的盲分离算法

3.1 时频域盲分离算法

盲分离的本质是根据信号统计特性设计分离函数J(W)，再利用某种准则使分离函数达到极值求解W的过程。分离信号y(t)是源信号s(t)的估计

y(t)=Wx(t)=WAs(t)

(8)

解混矩阵W=U#B，U是酉矩阵，#表示伪逆，B是白化矩阵。

白化处理的目的是减小接收信号相关性，x(t)白化后信号z(t)=B·x(t)，其自相关函数满足Rz=E[zzH]=I。计算z(t)的WVD时频分布

Dz=BDx(t，f)BH=UDs(t，f)UH

(9)

式中，U=BA称为酉矩阵，Ds是x(t)的WVD分布矩阵，Dz的对角线元素dii(t，f)，i=1，2…，n代表源的自项时频分布，非对角线元素dij(t，f)，i，j=1，2…，n代表源间互项时频分布。在单目标亮点自项时频分布(ta，fa)上，其WVD时频分布Ds(ta，fa)为对角阵[10-11]，

Ds(ta，fa)=UHDz(ta，fa)U

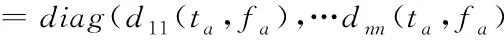
(10)

但对信号处理时存在数值计算误差和环境干扰，实际声纳目标回波的时频分布Ds不可能是理想的对角阵，可通过使其非对角线元素之和最小求解酉矩阵，利用目标时频点集进行联合对角化处理，有

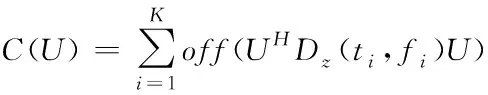
(11)

其中，(ti，fi)属于目标亮点自项时频集合Ωs′。

可见，目标源时频自项分布集提取的准确性直接影响盲分离的性能。研究利用形态学滤波去除时频面的混响及互项，以提高目标源自项时频点集提取的准确性。

3.2 结合形态学滤波的分离算法设计

图像形态学滤波根据不同信号的图像特征差异，通过选择合适的结构元，滤除图像中比结构元尺度小的噪声干扰，达到抑制干扰、突出目标图像的目的[12]。其中，腐蚀操作可以去除图像中尺寸小于结构元的任意图像，而膨胀又将图像中的缝隙填充为指定宽度，弥补腐蚀操作对目标图像的损失。

在观测信号WVD时频面上，选取与输入信号斜率相同的线状结构元，记为O。目标回波时频分布区域记为A，混响与互项干扰分布区域记为C，利用结构元O对集合A与C进行腐蚀与膨胀处理

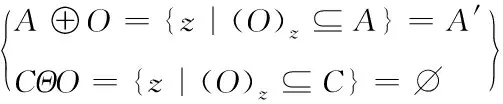
(12)

根据发射信号能量与最大传播损失估计接收目标回波能量ε，提取形态滤波后图像中能量大于ε的值建立目标源时频集合(t，f)∈Ωs。由于混响的分布具有随机性，使得部分目标源与混响的分布重叠，再对Ωs进行波形聚类优化处理，进一步剔除与干扰重叠的目标点集，由于混响是大量随机散射体叠加形成的，相位一致性差，与发射信号的相关性弱，计算Ωs中每一时频点对应信号的时域形式，取其与发射信号相关系数[13-14]μ>0.5波形对应的点集为目标时频点，优化后的目标时频集合记为(t，f)∈Ωs′。

形态滤波质量取决于结构元的形状和尺寸选取，为了滤除干扰，一般要求结构元形状要与目标图像结构尽量相似。利用形态滤波去除图3中的间断线，保留连续直线，假设间断线长度为5个采样点，每个像素点能量设为1。取结构元形状为平行连续线的短线段，当其长度从1到40变化时，计算形态滤波后输出能量与原始能量的比值

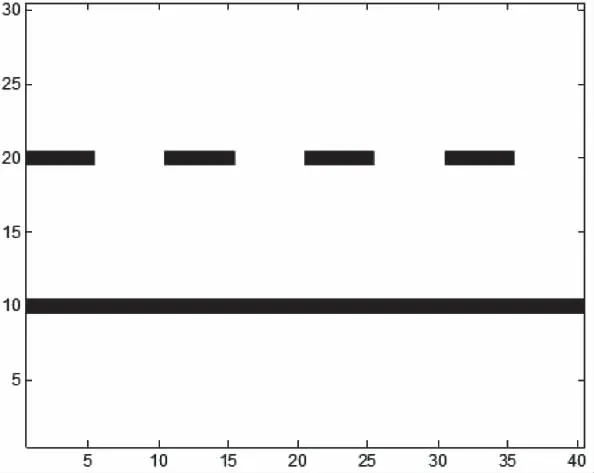
图3 待处理的图像

(13)

从图4可以看出，结构元长度超过间断线长度时α值趋于常数，间断线被完全滤除。因此，结构元长度通常要大于干扰尺度而小于目标图像的几何尺度。

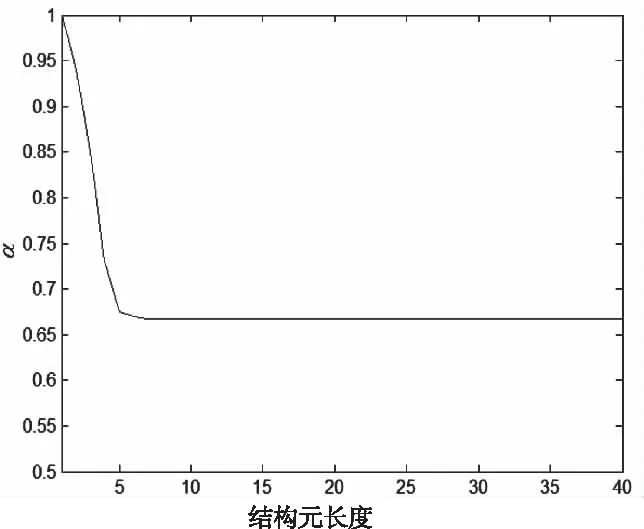
图4 结构元长度的选取

利用形态学滤波去除图1和图2中的互项干扰和混响。结构元取与发射信号同斜率的斜线，其长度取发射信号时宽的二分之一。处理结果如图5、6所示，图5中连续亮点之间的间断互项被滤除，目标亮点保留。图6中的混响被完全抑制，证明了算法的有效性。

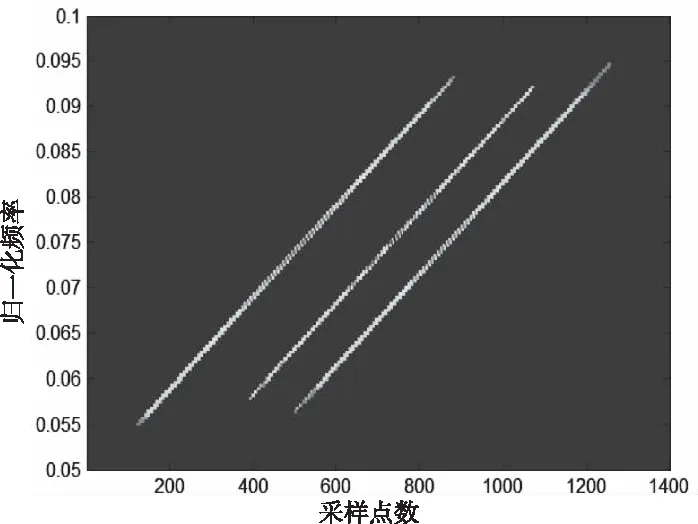
图5 形态滤波去除交叉项

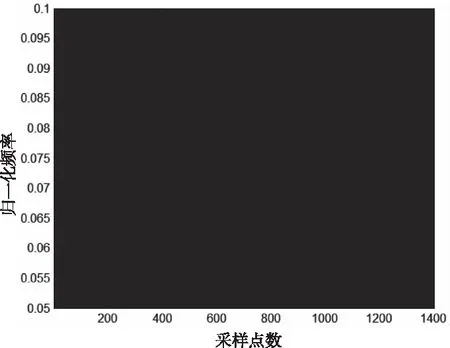
图6 形态滤波去除混响

4 算法分离性能分析与验证

4.1 算法分离性能对比

对比分析经典时频盲分离[15](TFBSS)和文中算法的分离性能，结果如图7所示，横轴代表输入信混比，纵轴代表输出信混比。

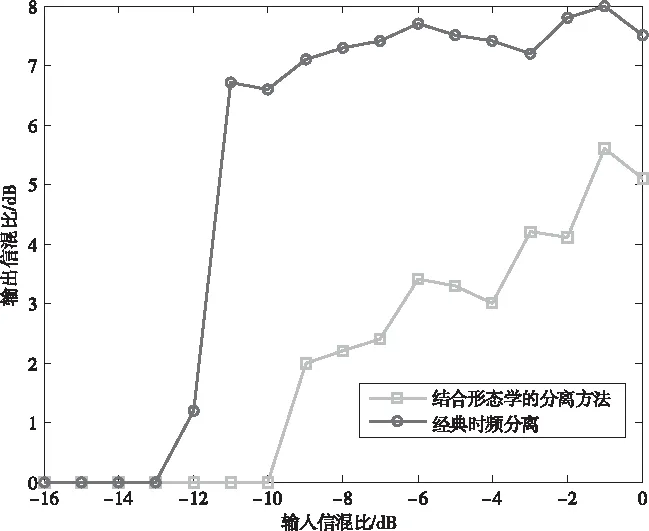
图7 算法分离性能比较

由图7可以看出，当输入信混比从-12dB到0dB变化时，结合形态学时频盲分离算法的输出信混比更高，验证了算法的有效性。但当输入信混比小于-12dB时，该算法的输出增益接近于零，这是因为目标回波特性受混响干扰严重，形态滤波方法不能有效区分目标与混响的时频特征，导致算法失效。

4.2 混响背景下的分离性能分析

构造四路阵元接收数据，根据亮点模型仿真三分量目标回波信号，取相同发射信号形式下湖试实验接收的实际混响数据，混合矩阵由0～1内均匀分布的4×3矩阵随机给出，SRR=0dB。

图8(a)为一接收阵元信号的时频分布图，很难观测到目标亮点的连续时频结构；图8(b)是该阵元信号与发射信号的相似系数，在采样点200，230和370处有三个明显峰值，是仿真的目标亮点，而其它位置处的峰值是由混响产生的。

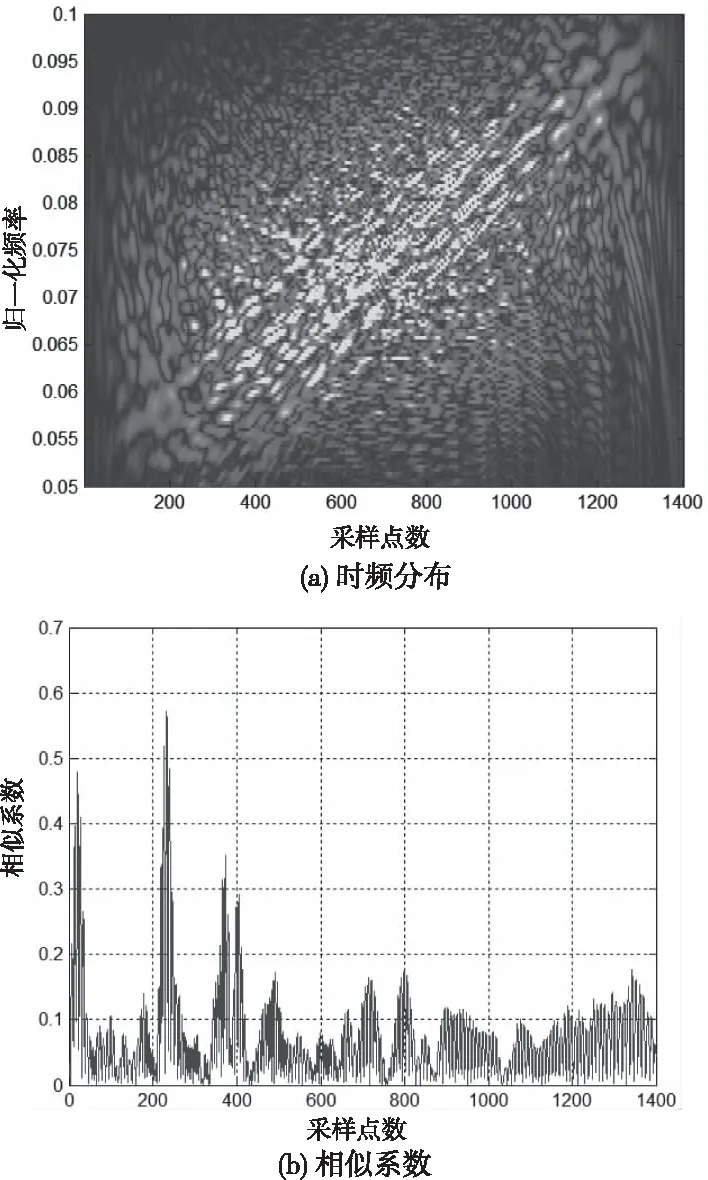
图8 观测信号

为了实现目标回波与混响的有效分离，需要抑制混响和交叉项，提取目标亮点的自项时频成分。

图9是形态滤波后得到的目标亮点时频集，可以看出，时频面上与目标亮点线谱不重叠的干扰项被完全抑制。根据2.2节内容，进一步优化与混响能量相重叠的目标时频点，取波形相似系数大于0.5时对应的时频分布点集作为参加联合对角化的目标信息，如图10所示。

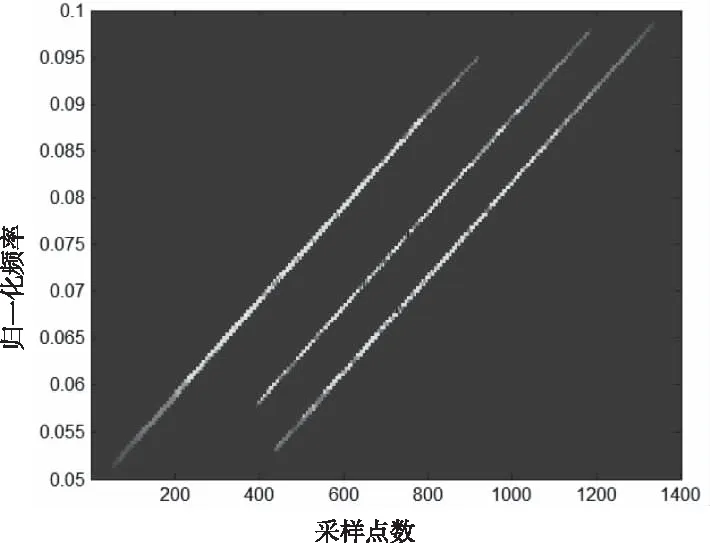
图9 目标回波亮点的时频点集

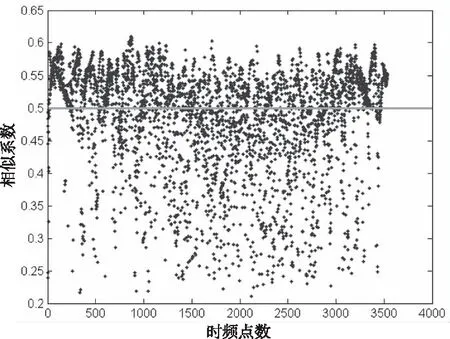
图10 时频信息优化估计

但与目标重叠的混响干扰点集做不到完全剔除，因此，需要讨论参加联合对角化的目标点集数目对分离结果的影响。仿真接收信号无混响，信混比分别为0 dB，-5dB，-10dB的四种情况。图11中横轴是参加联合对角化的目标自相时频点数，纵轴为得到的目标时域波形相似系数。设目标时频点总数为N点，能够清晰的看到，在不同输入信混比下，只要参加联合对角化的目标自相时频点数目大于N/5，得到的目标波形相似系数即可达到该输入信混比下的最大值。从图中也能看出，算法的分离效果还与输入信混比有关，这与仿真分析图1 的结果相符。

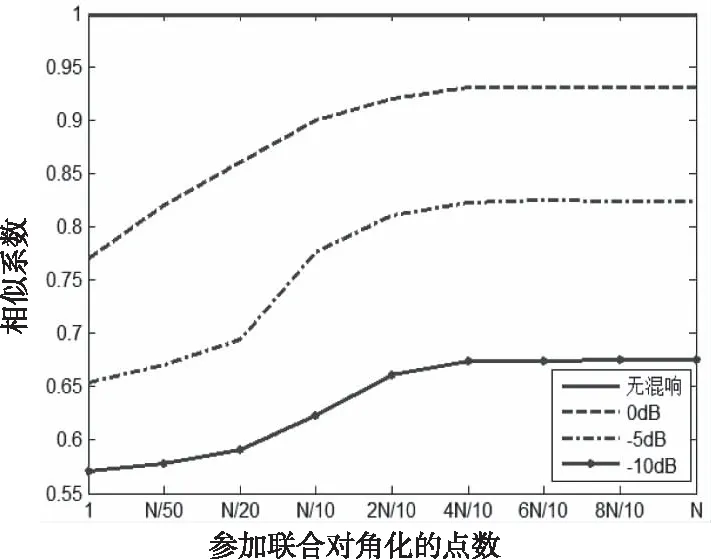
图11 自项点数选取对分离性能影响

对接收阵的混合信号进行目标回波分离，图12(a)、(b)分别为分离出的四路通道信号与发射波形的相似系数及其WVD时频结果，可以看出目标亮点存在于通道四中，并且，由环境干扰产生的谱峰得到了有效抑制，突出了目标谱峰，提高了输出信混比，为后续特征提取与探测识别提供了信号模型。

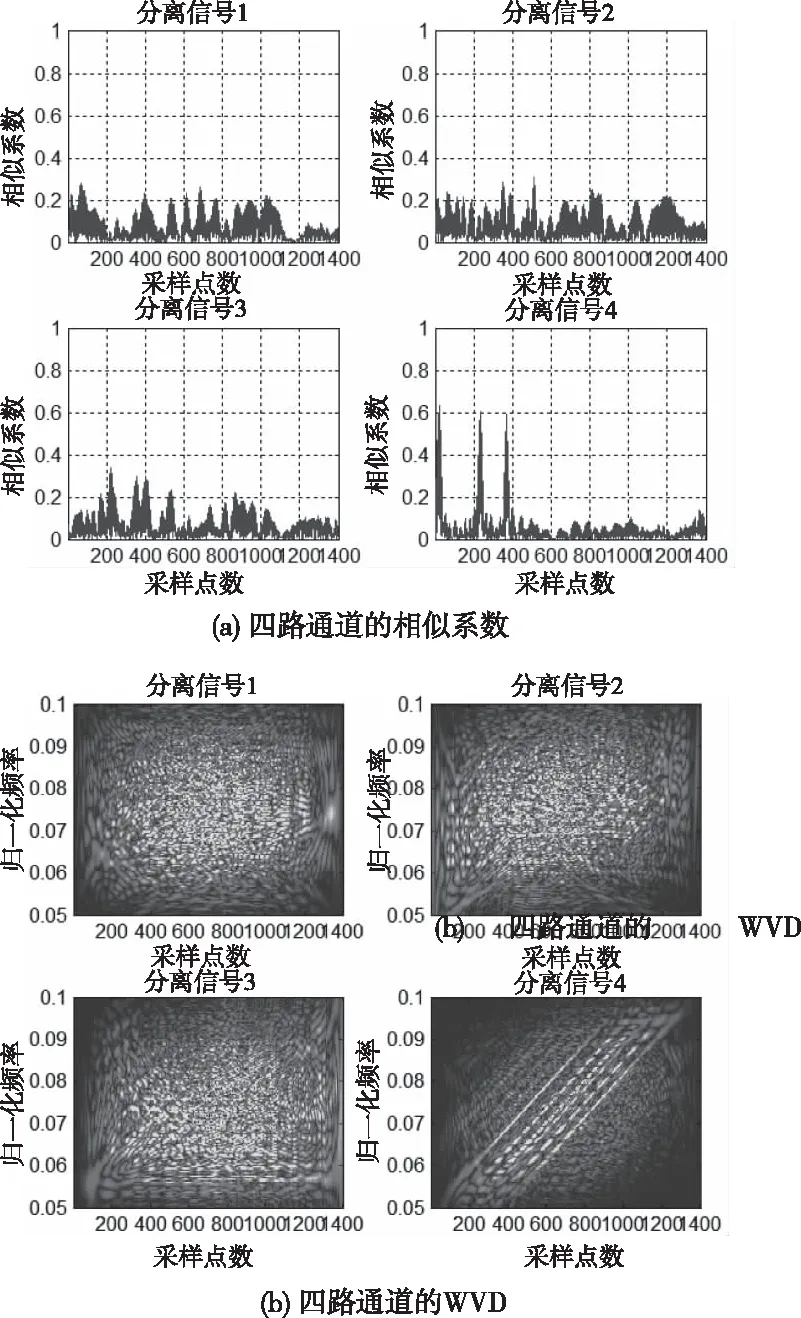
图12 混响背景下的多亮点分离

5 结论

海底混响是浅海目标探测识别的主要背景干扰，结合形态学滤波的时频域盲分离算法，根据目标亮点与混响的时频分布差异，通过准确的选择目标亮点自项时频点提高了时频盲分离的分离性能。数据仿真分析结果表明，①形态学滤波方法可以有效滤除与目标回波时频图像特征不同的干扰成分，提取出目标亮点自项信息，但提取性能受输入信混比影响。②与经典盲分离算法比较，文中算法不需要已知声纳信号能量的先验知识，通过提取出的目标自项时频点构建分离函数，获得了更高的输出信混比，为后续处理提供有效的目标回波信号模型。