基于反席卷法的高超声速飞行器最优制导律

林 灵，郭晓林

(1. 中国民用航空飞行学院，四川 广汉 618307；2. 中国民用航空西南地区空中交通管理局重庆分局，重庆 401120；)

1 引言

再入飞行器的制导律设计通常可分为标称轨迹制导[1-4]和预测校正制导[5-10]。预测校正制导是根据实际轨道的预报落点与预定落点之间的偏差值对控制量进行校正。标称轨迹制导是设计反馈控制律消除扰动，使再入飞行器始终沿着基准轨迹飞行。两种设计方法各有利弊，自适应方法可以适应飞行过程中由于故障或任务改变而进行的轨迹调整，但由于在每一个制导周期内都对飞行轨迹进行重新规划，计算量较大，因而对再入飞行器的在线计算能力和信息存储容量要求较高[11]。标称轨迹制导主要包括离线标称轨迹规划与在线轨迹跟踪两部分，在最优轨迹确定以后，通过设计反馈控制律消除跟踪偏差可以实现高精度制导，且计算量小，工程上易于实现。

本文所设计的制导律基于标称制导体制，传统的标称制导律通常是使实际状态量尽快的接近标称状态量，而没有考虑为了消除扰动所形成的实际修正轨迹的最优性。本文在设计反馈控制律时，考虑到扰动所形成的偏差偏离原最优标称轨迹的范围并不大，因而引入了邻域最优控制理论，从而保证修正轨迹的最优性。在计算反馈控制量时，基于标称轨迹的数据，采用反席卷法[12]建立终端席卷变量的微分方程，逆向进行积分计算，因此求解最优反馈修正量的过程中并没有进行迭代计算，提高了计算效率，保证了算法的在线实施。

2 再入制导标称轨迹

2.1 再入运动数学模型

不考虑地球自转带来的影响，无动力高超声速再入飞行器的运动模型如下。状态量为x=(r，φ，θ，v，γ，χ)，r表示飞行器与地心的距离；φ，θ分别表示经度与纬度；v表示速度、γ与χ分别表示航迹倾角、航迹偏角；控制量为u=[a，β]，a，β分别表示攻角和倾侧角。

(1)

式中，m表示飞行器质量，g表示重力加速度，L，D分别表示升力和阻力

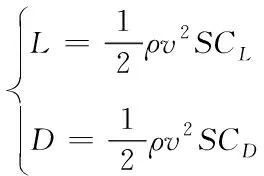
(2)

式中，ρ为大气密度，S为参考面积，CL，CD分别表示升力系数与阻力系数，其表达式如下，具体参数参考文献[13]

(3)

2.2 轨迹优化模型

轨迹优化即求解控制量u=[a，β]使目标函数最小(或最大)，并且满足状态微分方程及一系列终端及过程约束条件。为了再入飞行器的横向机动最大，通常区精度最大为性能指标

J=Φ(x(tf)，tf)=-θf

(4)

再入飞行过程中需要严格满足动压、过载及热流密度及控制量约束

q=0.5ρv2≤qmax

(5)

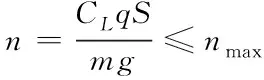
(6)

(7)

umin≤u≤umax

(8)

在终端时刻需要满足位置、速度和角度等约束条件

(9)

针对以上的再入轨迹优化模型，先采用伪谱法将其转化为非线性规划问题，再采用非线性规划求解器SNOPT[14]等进行求解。具体参数设置参考文献[13]，仿真结果如图1至图3所示。

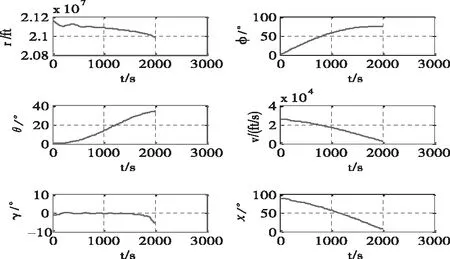
图1 标称轨迹

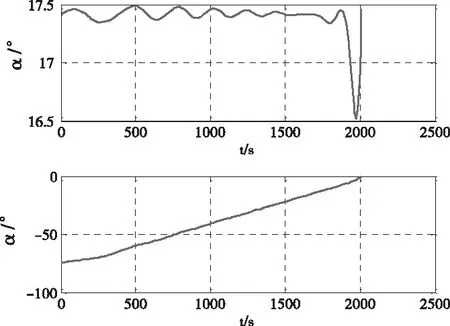
图2 标称控制量

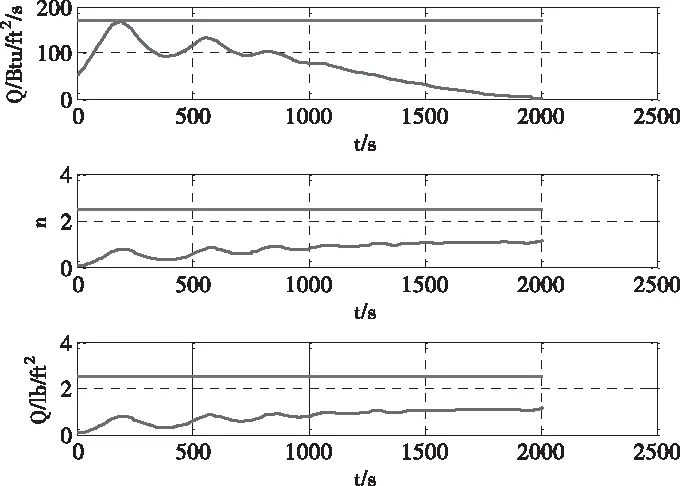
图3 过程约束

3 基于反席卷法的制导律设计

由于建模误差及外界随机干扰，通常会造成飞行器的实际轨迹偏离标称轨迹，为了解决此问题，可以在线重新规划轨迹，但这种方法计算量大，工程上难以实现。本节考虑采用最优控制中的相关理论与反席卷法，通过最优控制理论得到协态量与终端偏差的微分方程后，引入席卷变量，推导席卷变量的微分方程及终端条件，进行逆向席卷，然后借助标称轨迹数据求得席卷变量，进而根据最优控制中的相关推导，求解跟踪控制律，得到最优修正轨迹。

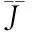
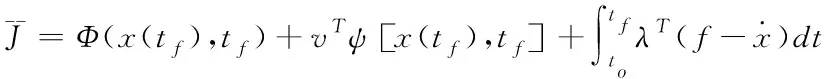
(10)

根据极小值原理，可得正则方程与耦合方程如下

(11)

(12)

式中，哈密顿函数为

H(x，u，λ，t)=λTf(x，u，t)

(13)

考虑到终端状态受约束，则边界约束条件为

x(t0)=x0

(14)

ψ[x(tf)，tf]=0

(15)

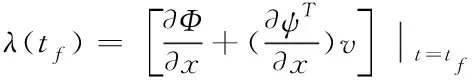
(16)

考虑飞行器实际飞行轨迹与标称轨迹的初始偏差δx(t)，初始偏差会产生状态量、协态量及控制量与最优参考轨迹的偏差，分别为δx、δλ和δu，对式(11)-(15)进行二阶变分，可得

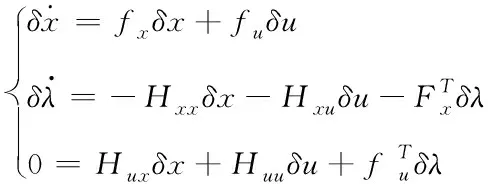
(17)

(18)

当矩阵Huu为非奇异矩阵时，可得

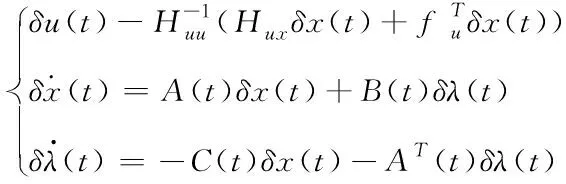
(19)

式中

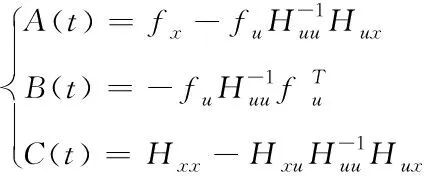
(20)

结合式(15)-(16)，引入席卷变量S，R和Q将δλ和δψ表示成关于拉格朗日乘子偏差dv和状态量偏差δx的线性关系

δλ(t)=S(t)δx(t)+R(t)dv

(21)

δψ=RT(t)δx(t)+Q(t)dv

(22)

对式(21)-(22)等号两边进行求导，考虑常量矩阵δψ和dv一阶导为零，可得

(23)

(24)

联立式(17)与式(22)-(23)，可以得到关于S，R和Q微分方程

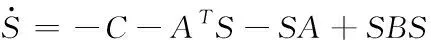
(25)

(26)

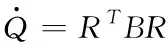
(27)

式(25)-(27)的终端约束条件应与式(18)相一致，所以可以得到如下的表达式

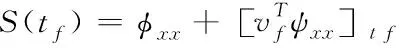
(28)

R(tf)=[ψx]tf

(29)

Q(tf)=0

(30)

根据微分方程(25)-(27)及其终端条件逆向进行积分，再联立式(22)，可以得到

dv=Q-1(t0)(δψ-RT(t0)δx(t0))

(31)

将式(31)代入式(21)中，可以得到协态量偏差的初始值

δλ(t0)=[(S-RQ-1RT)δX+RQ-1δψ]t0

(32)

由式(32)可以求出初始协态量偏差，结合初始状态量偏差，将两者代入式(19)中，即可得到任意时刻相应的最优状态修正量及最优控制修正量，进而实现了闭环的标称制导。本文所设计制导律的流程框图如图4所示。

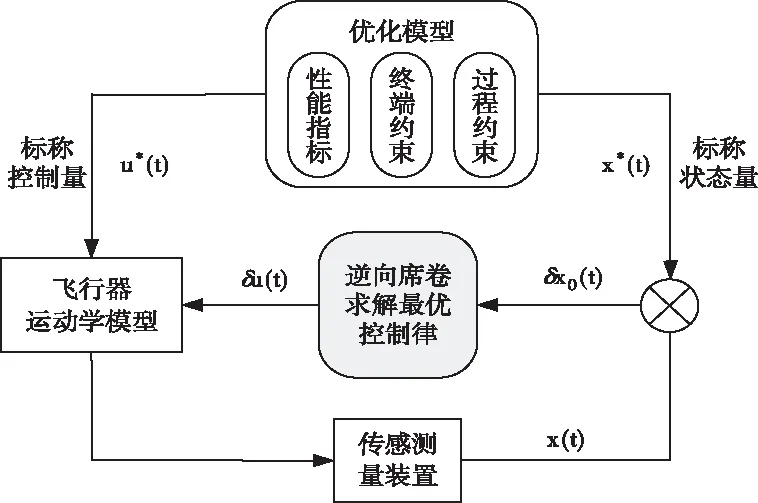
图4 最优制导律

4 仿真验证

为了验证本文所设计的制导算法的有效性，将表1中的初始扰动分别作为正值和负值加入制导回路中：

表1 初始扰动

为了便于比较，令Case 1和Case 2分别表示正值扰动和负值扰动，仿真所用的计算机配置为联想CPU 2.5GHz Intel Core i5处理器，仿真软件为MATLAB® R2014a。飞行器状态量偏差变化曲线如图5所示。过程约束的变化曲线如图6所示，图中Max表示约束上限。

由图5可知，在初始扰动存在的条件下，采用本文设计的反馈控制律所形成的闭环制导律，跟踪误差沿整条轨迹都不大，且最终收敛，验证了制导算法的有效性。由图6可知，采用本文方法得到的修正轨迹仍然满足热流、动压和过载等过程约束，因此保证了制导律的可实现性。

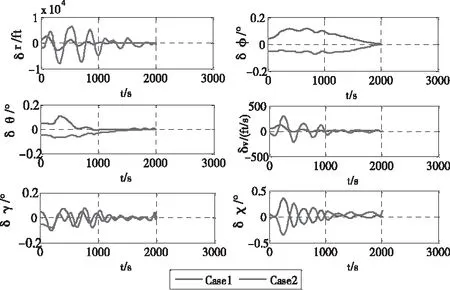
图5 状态量偏差

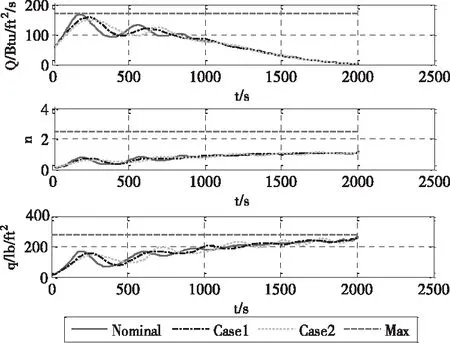
图6 过程约束

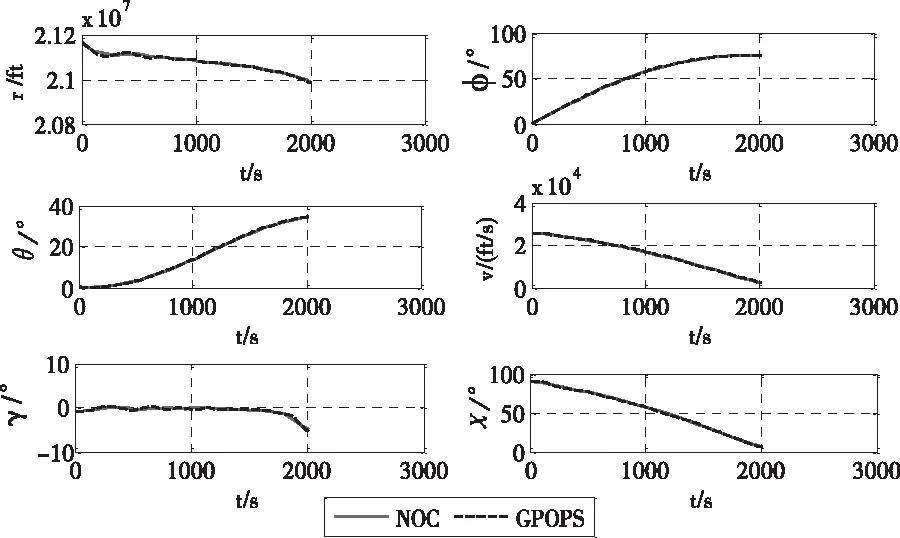
图7 轨迹对比

本文在设计反馈控制律时，考虑了消除扰动所形成的实际修正轨迹的最优性，为了验证这一优势，将采用本文制导算法所得到的修正轨迹与伪谱法重新优化所得到的轨迹进行了对比，由图7可知，两条轨迹基本重合，验证了本文所设计的制导算法的最优性。表2给出了本文方法与基于伪谱法重新优化的制导策略的消耗时间对比，由表2可知，本文方法的计算效率远远高于重新优化的策略，满足实时性的要求。本文方法计算效率大幅提升的原因为其利用原有标称轨迹数据，进行矩阵运算及积分求解最优反馈修正量，避免了迭代寻优计算，大幅降低了运算量。

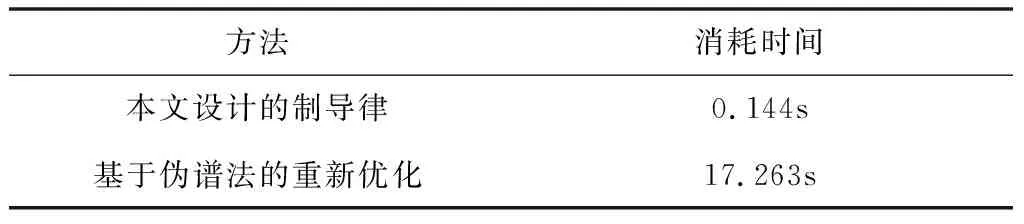
表2 消耗时间对比

5 结论

本文基于最优控制相关理论与反席卷法，设计了一种实时的标称最优制导律。所设计的制导律考虑了消除扰动所形成的实际修正轨迹的最优性，在状态量具有较大初始扰动的情况下具有良好的鲁棒性，且修正轨迹满足多种过程约束，保证了其可实现性。由于本文方法通过矩阵运算及积分求解最优反馈修正量，避免了迭代寻优计算，计算效率大幅提高，约为重新优化策略的120倍，且满足实时性的要求。