城市轨道爆破引发邻近建筑振动效应模拟研究

李中一，黄 静，梁乃兴

(重庆交通大学，重庆 400063)

1 引言

近年来，随着社会经济的快速发展，城市人口越来越多，城市规模不断扩大，城市化的生活给人们的生产和生活带来了便利，然而也带来了交通严重拥堵的城市问题。因此很多城市在发展的过程中，选择同步建设轨道交通来解决拥堵问题。就当前技术而言，爆破方法是建设城市轨道中最经济的施工办法。但是爆破方法会造成一系列的影响，如爆破中产生的粉尘、噪音和振动等，最严重的就是爆破振动，它会对邻近的建筑造成一定程度的损坏。因为炸药在爆炸的过程中有一部分能量转化为振动波通过介质不断传播，在一定范围内，振动波会引发质点剧烈振动，从而影响邻近建筑。通过爆破在一定范围内产生振动而引起的影响称之为振动效应[1-2]。如何在城市轨道建设中降低爆破振动效应是当前研究领域中的重点问题之一。在城市轨道施工前，对爆破产生的振动进行模拟分析是非常有必要的。近年来，大量学者在爆破理论及振动效应等方面做了相应的研究，但大部分都是针对质点位移、质点振动频率等方面的研究[3-6]，对质点振动效应的研究少之又少。

本文通过构建有限元楼房建筑物，分别从力学、验算和设计三个角度考虑，对炸药爆破过程中质点的振动位移、振动频率和振动速度三个方面进行模拟。利用Duhamel积分，通过褶积形式表示建筑物的结构位移、速度、加速度，并将爆破振动波形作为施加荷载，将楼房建筑视为一个简化的多自由度体系，求解出建筑物在振动过程中的实际振动位移。通过在楼房建筑底部安装爆破振动监控仪器对质点振动速度进行观察。监测结果表明，在爆破过程中本文提出的模拟结果具有良好的准确性。

2 构建有限元建筑与轨道模型

2.1 模型概述

建筑模型为6层高的楼房建筑物，每层高度为3m，宽度为8m，墙体厚度为0.3m，每根柱子之间的距离为6m，楼房建筑物的横梁截面积为0.045m2，柱子截面积为0.09 m2。城市轨道简化为由长度60m、宽度55m、高度40m的岩石构成，轨道直径为8.9m，将33kg的炸药装进直径为2.2m、长度为0.9m的圆柱体中，埋入地下30m深度处。

模型柱子、横梁采用钢筋混凝土材料，墙体采用砖和砂浆材料。各种材料的等级/型号如表1所示。

表1 模型等级/型号

2.2 模型参变量

模型采用三维结构实体单元，由在x、y、z三个方向上可以产生速度和位移的8个节点组成，这种模型非常适用于爆破数值模拟环境中[7]。考虑到应变率的影响，模型中岩石采用介质不连续、不均质的花岗岩为材料，花岗岩、钢筋混凝土和墙体的参变量如表2所示。

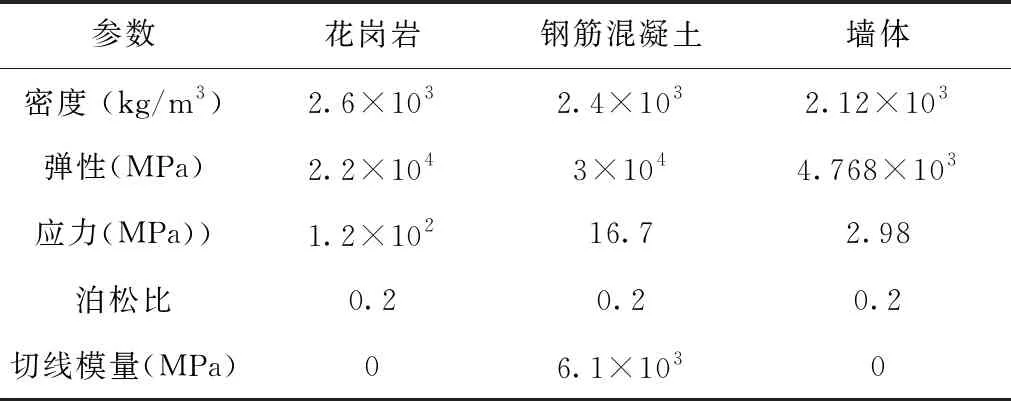
表2 花岗岩、钢筋混凝土和墙体的参变量

炸药采用高能材料数值模型，为了提高计算精度，通过气体压力与体积变化的状态方程Jone-Wikin-Lee进行描述。Jone-Wikin-Lee方程表示为

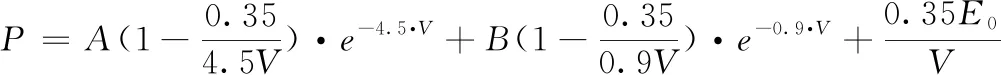
(1)

其中，A、B分别表示状态方程的参数值，A=2.64×105MPa、B=1.85×102MPa；P表示炸药产物所产生的压力；V表示相对体积；E0表示单位体积内炸药所具有的内能。

3 振动荷载模拟研究

通过动力有限元方程可以对岩石、钢筋混凝土和墙体的结构特征进行研究分析。有限元方程可以分别从力学、验算和设计三个角度考虑，并对炸药爆破过程中质点的位移、频率和振动速度三个方面进行模拟预测，为后期炸药爆破提供施工依据[8-10]。本文通过数值模拟的计算结果研究炸药爆破对邻近建筑的影响，从而进一步了解建筑物因爆破产生的振动效应。

依据爆破理论，假定爆破荷载均匀分布且竖直作用在轨道面上，为了充分研究爆破应力在轨道上的振动规律，选取加荷载时间为15ms，卸荷载时间为95ms，计算应力时间为10000ms。根据爆破荷载经验，荷载峰值用公式可表示为

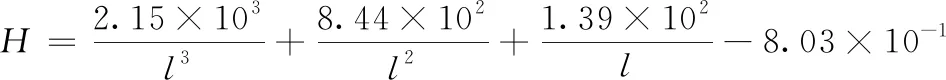
(2)

其中，l表示比例距离，由上式可以得出

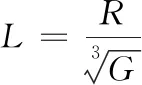
(3)

其中，R表示炸药爆破点距邻近建筑物的距离；G表示炸药的装药量。当建筑物的结构受到外荷载的影响时，建筑物结构的振动便属于地面干扰所造成的强迫振动效应，建筑物体系的运行方程用公式可表示为

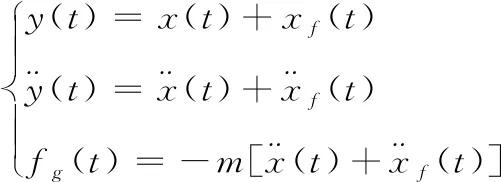
(4)

其中，y(t)表示绝对位移；x(t)表示相对位移；xf(t)表示地面支撑位移。整理后得

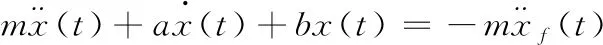
(5)

利用Duhamel积分，建筑物的结构位移、速度、加速度可以通过褶积形式用公式可表示为

(6)

对于楼房建筑物而言，其主要质量表现在楼体结构上，墙体为次要质量，因此可以把整个楼房建筑的质量集中到楼体质心位置，从而将楼房建筑视为一个简化的多自由度体系。假设某位置坐标j速度为1时表示为vij；在位置坐标i速度为0时，所受的阻尼力用公式可表示为

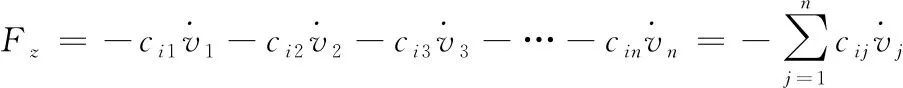
(7)

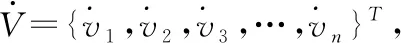
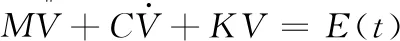
(8)

其中，M表示力矩；E(t)表示外荷载向量。一般求解方程的方法不利于求解积分方程的体系属性，因此本文采用振动叠加的方法求解方程，通过坐标变换，简化振动方程，从而把多自由度体系转换成为单自由度体系，将强迫振动方程分解为n个独立的微分方程，该过程用公式可表示为

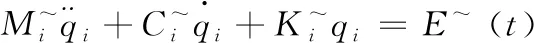
(9)

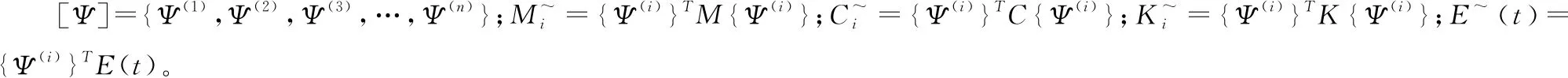
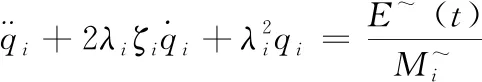
(10)

通过上式便可求出微分方程的稳态解，从而进一步得出对应的折算荷载，结合折算荷载的幅值，可以求出广义坐标向量q，用公式可表示为

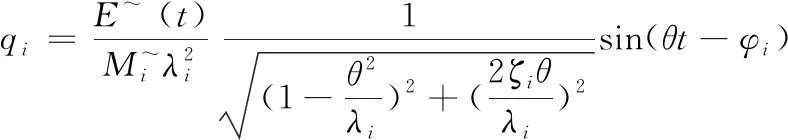
(11)

综上所述，便可求解出建筑物在振动过程中的实际振动模型。

4 爆破振动效应的动力响应

为了更加准确地体现出振动效应特征，本文选用爆破振动波形作为施加荷载。通过在楼房建筑底部安装爆破振动监控仪器对质点振动速度进行观察，由微分方程可得到质点的振动加速度曲线。本次实验炸药量为24kg，炸药距楼房建筑物的距离为44m，振动加速度的幅值为-4.822m/s2，持续时间为5.04s。经过微分处理后楼房建筑物的质点振动加速度曲线如图1所示。

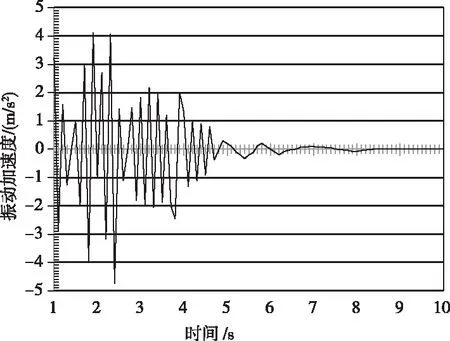
图1 振动加速度曲线

通过质点振动加速度曲线可以看出，楼房建筑物质点的振动加速度在时间为2.65s时幅值最大，表明振动的特别快。同时质点振动的加速度衰减相对也比较快，经过5.04s的时间，质点速度基本保持不变，能够维持一个稳定的状态。

将爆破振动荷载施加在楼房建筑底部，对楼房每一层楼顶处设置一个数据采集点，针对每层楼顶质点的位移和振动速度变化情况进行振动响应分析。计算结束后，各个数据采集质点的振动位移和振动速度曲线如图2和图3所示。

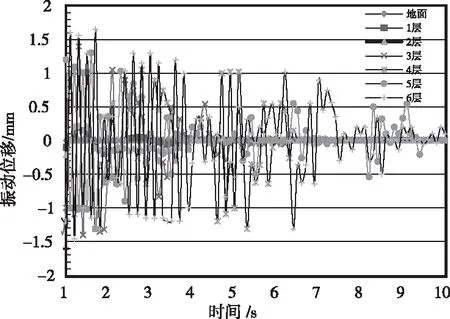
图2 振动位移曲线

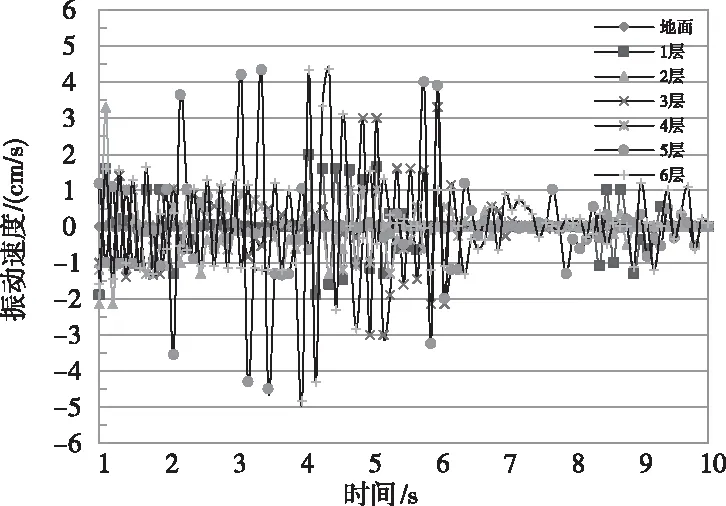
图3 振动速度曲线

通过采集点的振动位移曲线可以看出，楼房建筑物中下部质点的振动位移衰减特别快。而建筑物顶部(六楼)的质点振动位移则缓慢衰减，但质点振动位移的峰值显然大于楼房建筑物中下部的峰值位移。

通过采集点的振动速度曲线可以看出，楼房建筑物中下部质点的振动速度衰减特别快。达到楼房建筑物四层顶部时振动逐渐变得更加剧烈。相对于楼房建筑物质点的振动位移曲线，质点的振动速度曲线更加剧烈。

研究表明，在爆破振动荷载作用下，楼房建筑物的振动速度采样质点随着楼房高度的增高而增大。结合爆破安全规则标准，在建筑物附近进行爆破时，建筑物的最大振动速度不可超过5cm/s。

5 轨道爆破监测分析

在修建城区轨道时，对爆破点随机监测5次，每次都记录炸药爆破点到邻近建筑物的距离，对记录的数据进行回归研究，从而了解爆破所产生的振动波在邻近建筑物周围的传播规律。对监测到的数据应用回归法所获得的振动波衰减方程进行数据分析，结合爆破振动波衰减方程对爆破点到邻近建筑物之间的比例距离和质点的振动幅值进行回归分析，结果如图4所示。

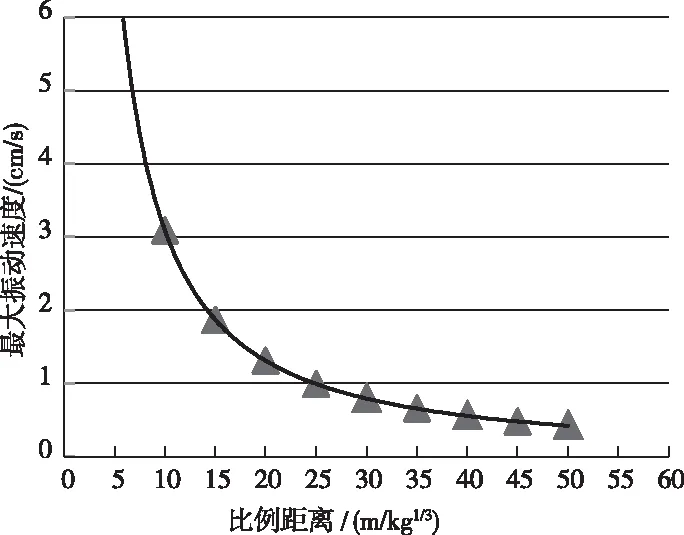
图4 爆破衰减回归分析

通过回归分析曲线，便可进一步求得轨道爆破时，邻近建筑物在爆破衰减公式中的相关系数大小，并求出爆破质点的振动公式

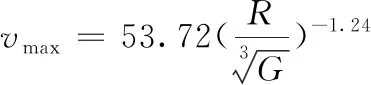
(12)

其中，vmax表示最大振动速度；R表示爆破点距邻近建筑物的距离；G表示最大用药量。通过以上研究分析可知，爆破过程中质点的振动具有随机性，通过经验回归分析关联性较好，满足爆破所产生的振动波在邻近建筑物周围的传播特性。通过式(12)可以测量爆破点到邻近建筑物的距离，进而确定轨道爆破过程中的最大用药量。

对爆破过程中采集的振动波进行傅里叶分析，可以求得振动波中较为有优势的频率，如图5所示。

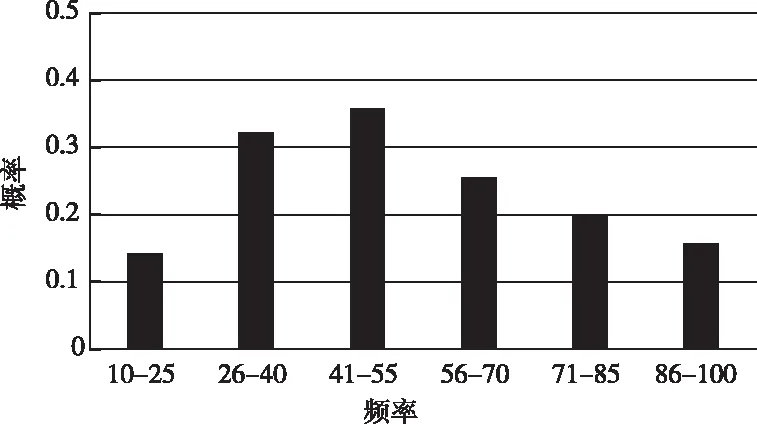
图5 频率分布图

由图5可以看出，爆破监测点的振动频率在26-70Hz之间的概率较大，振动频率在41 Hz-55 Hz之间的概率最大，说明爆破过程中振动波的频率在41 Hz-55 Hz之间时，建筑物可以处于一个相对稳定的状态。

综上所述，随着建筑物监测点位置的增高，质点最大振动速度会明显增加，说明本文模拟结果的准确有效。结合数值计算可知，通过质点的振动速度来控制建筑物的安全性较为合理。因此，在轨道爆破过程中，应该多注意邻近建筑物的振动速度。

6 结束语

由于建筑物结构的复杂性和爆破过程中振动波的随机性，研究爆破振动荷载的应力响应更加困难。在当前学者的研究基础上，本文对爆破过程中所引发的邻近建筑物振动效应进行模拟研究。首先构造建筑物模型、轨道模型以及炸药参数，然后通过动力有限元方程对岩石、钢筋混凝土和墙体的结构特征进行研究分析，从炸药爆破过程中质点的位移、频率和振动速度三个方面进行模拟。最后对爆破点进行随机监测，对监测到的数据应用回归法所获得的振动波衰减方程进行数据分析。证明了本文所提出的方法在爆破过程中模拟结果具有正确性、方案具有可行性，还可以更加全面地研究振动效应在有建筑物的环境中的传播规律。此外，结果表明通过质点的振动速度来控制建筑物的安全性较为合理。