无限长平行双导线电场的Mathematica可视化方法

杨能彪

摘要：利用Mathematica的强大符号运算功能，利用Mathematica推导出无限长平行双导线的解析表达式，并应用Mathematic的强大的绘图功能，实现了对无限长平行双导线电场的可视化，并与已知结果相比较，由此可以更加直观地了解复杂的电磁场变化的规律。

关键词：数学软件Mathematica;符号运算;可视化

一、问题的提出

如图所示，设一无限长平行雙导线置于空气中，介电常数为ε。两导体的半径均为a，且它们轴线间的距离为d，如图所示。首先利用Mathematica强大的符号运算功能，推导出无限长平行双导线电位的解析表达式，并应用Mathematic的强大的绘图功能，得到无限长平行双导线电场分布的可视化图形。

假设二线间距离较近，由于导体表面的电荷分布要受邻近导体的影响，因而失去轴对称关系。若先找出电荷分布再计算电场非常困难，所以设想用两根带电荷的平行细线来等效真正的表面电荷而保持导体表面的边界条件不变，由唯一性定理，说明边界条件不变，原来问题的解也不变。

现在假设两导体表面单位长度总的带电量为+ρl、-ρl，由于异号电荷相互吸引，两导体的内侧较外侧电荷密集，故两平行细线电荷偏离原来轴线，相互靠近，令它们与坐标中心o的距离分别为h，在直角坐标系中，由Mathematica的符号推理功能可得，可以得到电位如下：

二、利用Mathematica实现无限长平行双导线电场的可视化

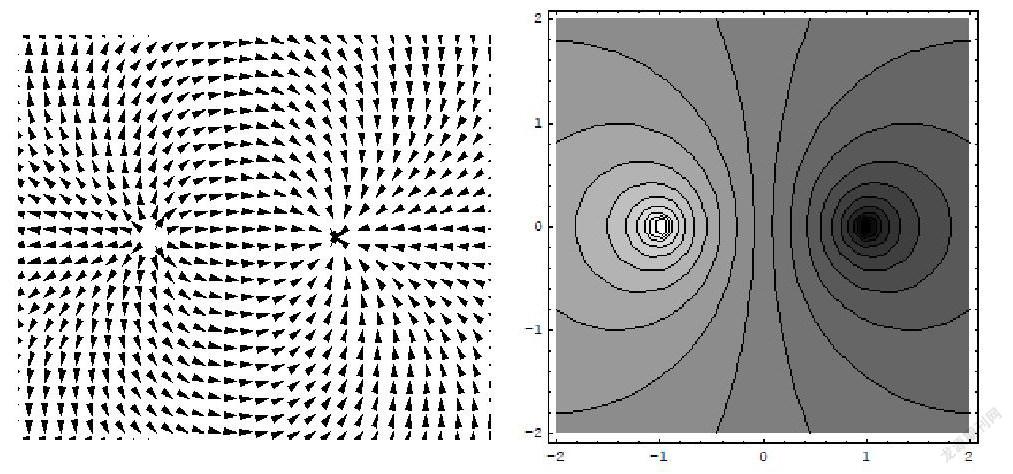
利用Mathematica矢量分析软件包，设定适当的参数，可以绘制出无限长平行双导线电场矢量线的分布。此时，需要调用Mathematica图形软件包ContourPlot以及ShowGraphics，然后可以绘制出其电位线可视化图形如图所示。

三、结论

数学软件 Mathematica具有强大的数值计算、符号运算和图像可视化甚至是逻辑推理的功能，使用起来非常便捷。通过利用Mathematica强大的图像可视化功能，能够很直观地看到无限长平行双导线中的电场、电位的变化规律，通过可视化，可以很方便地研究电场中的某一点、某一区域的电场电位的分布情况，这给我们研究电磁场问题，总结电磁场的规律提供了很大的便利。

参考文献：

[1]杨儒贵.电磁场与电磁波[M].北京，高等教育出版社，2003

[2]钟顺时《电磁场理论基础》西安电子科技大学出版社1995年6月第一版

[3]王雪君《电动力学解题指导》北京师范大学出版社1998年6月第一版

[4]邓建松，彭冉冉译.尤金D .Mathematica使用指南.北京：科学出版社，2002.

[5]丁大正.科学计算强档Mathematica4教程[M].北京，电子工业出版社，2002