某单向壁板连接的钢筋混凝土群仓设计

胡正冬

南京丰源建筑设计有限公司 210012

引言

面粉厂储存小麦的群仓一般可以设计成方仓群仓或者筒仓群仓，方仓的建设费用比筒仓高，设计时可优先选用筒仓群仓。但如果筒仓的直径较小，那么筒仓围合成的星仓仓容更小，生产使用时会有很多弊端。采取措施扩大星仓仓容，既能降低造价又便于生产。

本文工程群仓中的筒仓一侧采用壁板相连，此措施扩大了星仓的仓容，相比于方仓群仓节省了300多万的建设成本。群仓经过五年的投产使用，效果良好，受到了推崇。

由于筒仓设计规范并未涉及此种形式，国内也没有建成的先例可供参考，故本工程结合现有规范［1，2］计算方法，基于SAP2000结构有限元计算软件探讨壁板相连群仓设计时需要注意的问题，为此种仓型设计和推广提供一定的参考。

1 工程概况

群仓由3排8列共24个筒仓连接而成，排方向筒仓筒壁外圆相切连接，列方向筒仓之间由壁板连接，围合成2排7列共14个星仓，如图1所示。筒仓仓壁高度为27.3m，壁厚180mm，外径D＝6.7m，内径d＝6.34m，星仓壁板长度2.1m；仓下为筒壁支撑，筒壁顶标高为＋6.0m，筒壁底标高为-1.2m，壁厚220mm，外径6.7m，内径6.26m，筒壁根据工艺要求设置宽2m、高3.6m的洞口；星仓壁板厚度为300mm，基础采用桩筏筏板基础。筒仓剖面见图2，星仓剖面见图3。

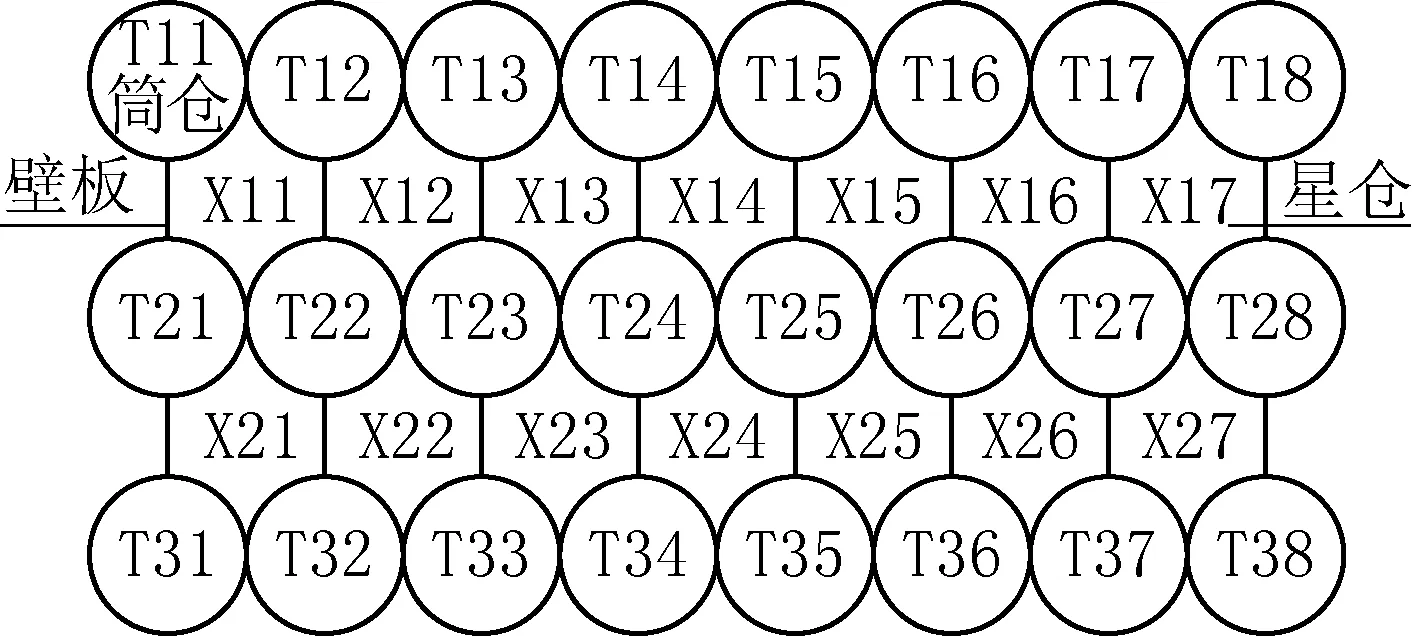
图1 群仓平面示意Fig.1 Group silos plan

图2 筒仓剖面示意Fig.2 Group silos vertical section

图3 星仓剖面示意Fig.3 Interstice silos vertical section

2 静力荷载作用下群仓有限元计算

《粮食立筒库设计规范》（LS8001—2007）中提及：外圆相切的的圆筒仓群仓的仓壁，可按单仓进行计算［1］。

《钢筋混凝土筒仓设计标准》（GB50077—2017）中提及：圆形群仓除应按单仓计算外，还可在空仓、满仓不同荷载条件下，使用程序或附录G的计算公式进行验算［2］。

对于外圆相切的小直径群仓根据设计经验一般可按单仓计算，虽然不能反映筒仓的实际受力状态，但可以满足使用要求。虽然本工程群仓属于小直径群仓，但在列向采用壁板相连，设计时应考虑壁板对群仓的影响。

2.1 主要计算参数

筒仓储存物料为小麦，小麦容重γ＝8kN/m3，摩擦系数μ＝0.4，侧压力计算系数k＝0.4059，储料计算高度hn＝27.3m，单仓和群仓的外仓水平压力修正系数Ch＝2.0，群仓的内仓和星仓水平压力修正系数Ch＝1.0。筒仓水力半径ρ＝6.34/4＝1.585m，星仓水力半径ρ＝1.174m。筒仓和星仓采用杨森公式［2］计算水平压力Ph＝Chγρ（1-e-μKSi/ρ）/μ。筒仓采用SAP2000有限元软件计算，仓壁、壁板、筒壁、顶板和底板采用壳单元模拟，环梁和顶板梁采用框架单元模拟，仓壁与仓壁相连处构造采用实体单元模拟［3］。

2.2 三列式群仓不利工况组合

本工程筒仓有8列，如果完整建立模型则需要考虑太多的工况组合，为简化计算，取具有代表性的三排三列作为计算单元。三列式群仓有多种装粮组合，将9筒仓满仓工况分别编号为T1～T9、星仓满仓工况分别编号为X1～X4，如图4所示。为了找出不利工况组合，在仓壁高度12m处按图4中标记的位置选取节点，并统计所有工况在节点处的内力。根据统计结果，舍弃对结果影响较小的工况，得出相对不利的工况组合。

图4 三列式群仓计算单元平面示意Fig.4 Calculation unit plane of three row group silos

1.仓壁（除星仓弧板）不利工况组合

角部的筒仓选取D1点，边部的筒仓选取D2、D4点，所有工况结果汇总见表1。

表1 仓壁（除星仓弧板）不同工况内力Tab.1 Resultant forces of silos wall（except arc walls of interstice silos）under different load cases

通过表1可知：仓壁（除星仓弧板）弯矩基本可以忽略；仓壁（除星仓弧板）在其满仓时拉力最大，其他仓满仓时增加的拉力占比小于5%，仓壁（除星仓弧板）可按单仓轴心受拉构件设计，设计时内力可按增加5%来考虑。

2.星仓弧板不利工况组合

选取星仓弧板在仓壁外圆相切连接加强处、弧板中间处和弧板与壁板连接处三个内力较大位置作比较，经统计三个位置不利工况组合一致。选取外圆相切连接加强处A1、A2、A4、A5点，统计所有工况结果见表2。

通过表2可知：星仓弧板在两侧的筒仓和星仓满仓时产生不利内力，其他工况占比很小。星仓弧板需要按偏心受拉构件设计。

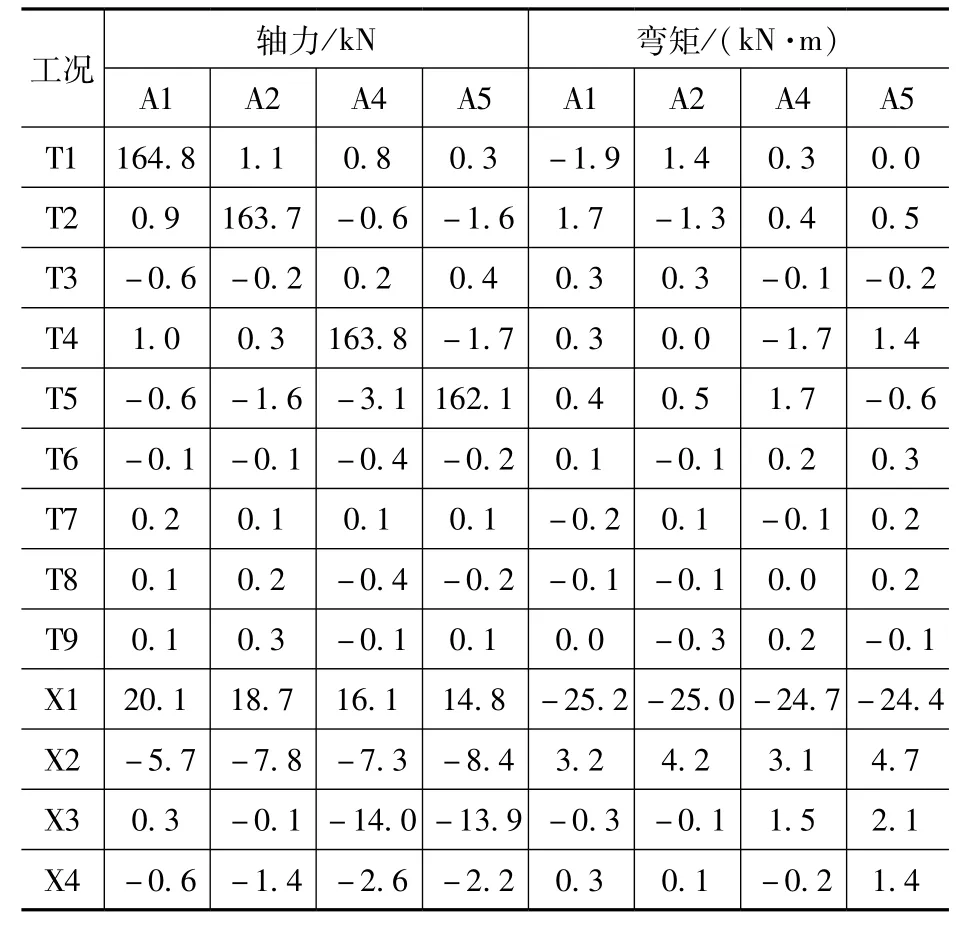
表2 星仓弧板在仓壁外圆相切连接加强处不同工况内力Tab.2 Resultant forces of interstice silos arc walls（on the tangent of silo walls）under different load cases

3.星仓壁板不利工况组合

壁板端部选取E1、E2点，壁板中部选取F1、F2点，所有工况结果汇总见表3。

通过表3可知：外侧壁板在星仓满仓时产生不利内力，其他工况占比很小，壁板按偏心受拉构件设计；内侧壁板存在两种不利工况，一侧星仓满仓时壁板需要按偏心受拉构件设计，两侧星仓满仓时壁板需要按轴心受拉构件设计，其他工况占比很小。

表3 星仓壁板不同工况内力Tab.3 Resultant forces of wall under different load cases

2.3 三列式群仓有限元计算结果汇总比较

将仓壁从底部到顶部按2m间隔统计内力。

1.仓壁（除星仓弧板）有限元计算结果

选取不利工况组合T1＋T2＋T4，将仓壁上D1、D2、D4点环向拉力与杨森公式计算拉力对比见图5。仓壁（除星仓弧板）环向拉力与杨森公式结果基本吻合，故设计时可采用单仓计算结果。仓壁顶部受到顶板约束，仓壁底部受到筒壁、环梁、底板和锥斗的约束，因此仓壁顶部和底部与杨森公式结果有出入，设计时在仓壁底部和顶部应适当加强。

图5 T1＋T2＋T4工况环向拉力与杨森公式计算拉力Fig.5 The horizontal tension of silo walls and the tension of Jansen formula under T1＋T2＋T4

2.星仓弧板有限元计算结果

选取不利工况组合，星仓弧板在角部筒仓处选用T1＋X1，星仓弧板在X向边部筒仓处选用T2＋X1，星仓弧板在Y向边部筒仓处选用T4＋X1，星仓弧板在中心筒仓处选用T5＋X1。

将A1、B1、C1点环向拉力与杨森公式计算内力对比见图6，在大约0.2倍仓壁高度以上星仓弧板环向拉力大于杨森公式结果，最大拉力出现在大约0.4倍仓壁高度位置附近。

图6 T1＋X1工况环向拉力与杨森公式计算拉力Fig.6 The horizontal tension of interstice silos walls and the tension of Jansen formula under T1＋X1

此种情况分析如下：常规外圆相切的星仓弧板按无铰拱简化计算，星仓满仓时弧板轴力为压力。如图7所示星仓满仓时从仓壁底至0.4倍仓壁高度拱脚的位移越来越大，随着高度增加星仓壁板处拱脚效应逐渐减弱，星仓弧板轴力沿着高度很快由压力变成拉力，轴力见图8。筒仓装满的情况下弧板轴力也是拉力，在底部至0.2倍仓壁高度范围内仓壁拉力与星仓弧板压力叠加后拉力小于杨森公式计算拉力，0.2倍仓壁高度范围以上仓壁拉力与星仓弧板拉力叠加后大于杨森公式计算拉力。

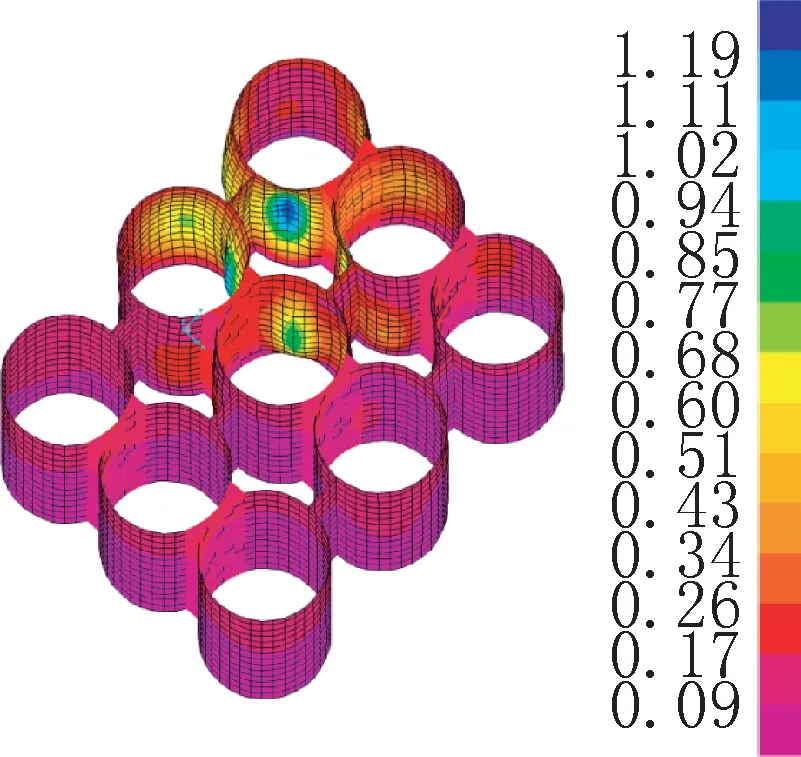
图7 X1工况仓壁变形（单位：mm）Fig.7 Deformation of interstice silos under X1（unit：mm）

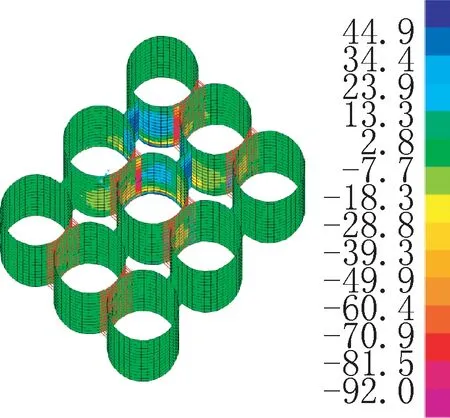
图8 X1工况仓壁轴力（单位：kN）Fig.8 The horizontal tension of interstice silos under X1（unit：kN）

A1、B1、C1点沿环向弯矩见图9，最大弯矩出现在大约0.4倍仓壁高度位置附近，端部A1、C1点弯矩与中间B1点弯矩反向。

图9 T1＋X1工况仓壁弯矩ig.8 The moment of interstice silo arc walls under T1＋X1

经过计算复核，星仓弧板需要按偏心受拉构件计算配筋，不能采用单仓计算结果，最不利处出现在0.4倍仓壁高度附近。

在角部筒仓处的星仓弧板内力大于边部筒仓和中间筒仓处星仓弧板内力，考虑到内力相差并不是太大，设计时可偏于保守选择角部筒仓上的星仓弧板计算结果。

3.星仓壁板有限元计算结果

选取不利工况组合，边部星仓壁板选用X1，中间星仓壁板选用X1和X1＋X2。

壁板在X1工况的拉力见图10，弯矩见图11，边部星仓壁板的内力大于中间星仓壁板内力。

图10 X1工况各点轴力Fig.10 The horizontal tension of walls under X1

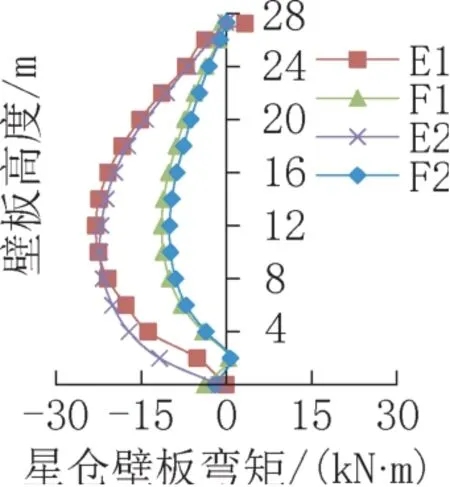
图11 X1工况各点弯矩Fig.11 The moment of walls under X1

中间星仓壁板在不利工况X1＋X2下的弯矩为0，轴力是单侧满仓工况X1的2倍。设计时需要按单侧满仓偏心受拉计算和两侧满仓轴心受拉计算包络设计。

3 地震作用下筒仓计算

《构筑物抗震设计规范》（GB50191—2012）提及：筒仓的水平地震作用，可采用振型分解反应谱法或底部剪力法计算。6度～8度时，钢筋混凝土筒承式圆形筒仓的仓壁与仓底整体连接时，仓壁、仓底可不进行水平地震作用的抗震验算，但其构件应满足相应的抗震构造措施要求［4］。

《钢筋混凝土筒仓设计标准》（GB50077—2017）提及：筒仓的水平地震作用可按底部剪力法进行计算。圆形筒仓的仓壁与仓底结构整体连接且筒壁开洞符合一定的要求时，仓壁和仓底可不进行抗震验算［2］。

本工程抗震设防烈度为7度，筒壁开洞满足规范［2］要求，抗震构造措施满足规范［2］要求，考虑到壁板连接形式可能存在的抗震不利影响，采用规范［2，4］提及的设计方法进行地震作用计算。

3.1 计算参数

抗震设防烈度为7度，设计基本地震加速度值为0.10g，设计地震分组为第一组，场地类别属Ⅲ类，场地特征周期值为0.45s。时程分析所用地震加速度时程的最大值：多遇地震为35cm/s2，罕遇地震为220cm/s2。储存物料重力荷载代表值取物料总重的80%，重心取物料总重的中心［2］。

3.2 多遇地震作用下的弹性变形

本工程多遇地震作用采用振型分解反应谱法进行计算。模态分析结构自振周期与频率结果见表4。如图12所示，第1、2振型以平动为主，第3～6振型皆以扭转为主，主要是角部筒仓和边部筒仓扭转，本工程群仓与普通外圆相切群仓振型相似。筒仓各标高多遇地震工况下X向和Y向位移见图13。

表4 满仓结构自振周期与频率Tab.4 Period and frequency

图12 群仓第1～6振型Fig.12 Modes1～6

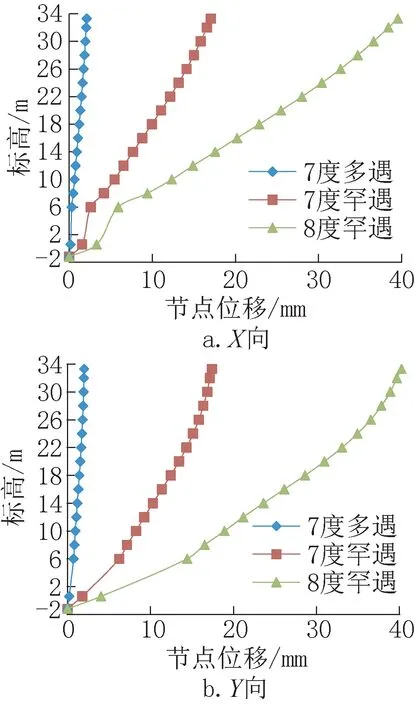
图13 筒仓各标高地震工况节点位移Fig.13 Nodes displacement of earthquake

3.3 罕遇地震作用下的弹塑性变形

根据规范要求，选择了2条天然波和1条人工波。弹性时程分析时，每条时程曲线计算所得结构底部剪力不小于振型分解反应谱法计算结果的65%，3条时程曲线计算所得结构底部剪力的平均值不小于振型分解反应谱法计算结果的80%。选出满足要求的3条波后，将地震加速度时程最大值调整为220cm/s2，计算罕遇地震作用下的结果并取3条波结果的包络值。

考虑到本工程所在地区抗震设防烈度不高，现将其调整到8度0.3g，地震加速度时程最大值调整为510cm/s2，并计算罕遇地震作用下的位移。

筒仓各标高在7度和8度0.3g地区罕遇地震工况下X向和Y向位移见图13。

3.4 地震作用下的变形验算

将筒壁和仓壁各视作一层，计算统计出筒仓的层间位移角见表5。筒壁X向位移角显著小于Y向位移角，主要原因是筒壁开洞减小了筒壁Y向刚度。仓壁X向位移角接近Y向位移角。

表5 群仓层间位移角Tab.5 Story drift ratio

规范［4］没有提及筒承式筒仓的层间位移角限值，本文参照钢筋混凝土剪力墙结构，其弹性层间位移角的限值为1/1000，弹塑性层间位移角的限值为1/120。群仓在7度多遇地震作用下弹性层间位移角远小于限值1/1000，能够满足“小震不坏”的抗震设防标准；其在7～8度罕遇地震作用下弹塑性层间位移角小于限值1/120，能够满足“大震不倒”的抗震设防标准。

4 结论

本文基于SAP2000有限元软件，建立了单向壁板连接群仓的模型，找出了不利工况组合，分析了仓壁和壁板的受力情况，计算了地震作用下的筒仓变形，得出结论如下：

1.小直径群仓可采用单向壁板连接的形式。

2.仓壁不含星仓弧板部分可以按照单仓计算设计。

3.星仓弧板在0.4倍仓壁高度附近内力最大，需要按偏心受拉构件计算设计，不能采用单仓计算结果。

4.外侧壁板按偏心受拉构件设计，内部壁板需要按偏心受拉构件和轴心受拉构件包络设计。

5.群仓在满足规范要求的抗震构造措施时，能够达到“小震不坏，大震不倒”的设防标准。

6.考虑到壁板的不利因素，设计时壁板厚度建议采用仓壁厚度的1.5～2倍，壁板与仓壁连接处建议采用加腋措施。