三角形二维周期结构光栅的衍射场
刘有菊 杨庆辞 何正英
(保山学院,云南 保山 678000)
目前,对光的衍射研究多数在于单孔的衍射,而对二维多孔的衍射研究较少。然而光谱仪、近眼显示(NED)系统等都涉及到多元多维结构光栅的衍射。三角形二维周期结构光栅是由N1列N2行全同三角形小孔按一定周期排列而成,是一种复杂的光学光栅。
1 三角形二维周期结构光栅的衍射实验
如图1所示,三角形二维周期结构光栅是由边长为a、b、c的全同三角形组成,其三角形沿x轴方向的空间周期为d1,共有N1列;沿y轴方向的空间周期为d2,共有N2行;这块光栅共有N1×N2个排列有序的全同三角孔构成,光栅的有效宽度为D1=N1d1,有效长度为D2=N2d2。
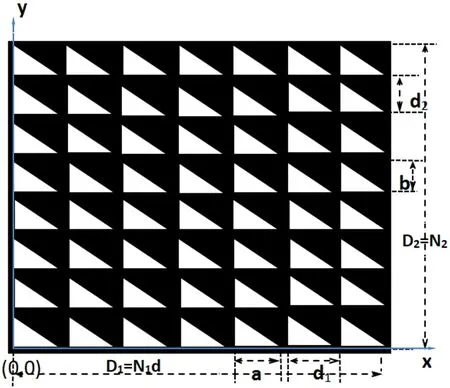
图1 三角形二维周期结构光栅
三角形二维周期结构光栅衍射的实验装置主要由三角形二维周期结构光栅、薄透镜、接收屏等组成,如图2所示。
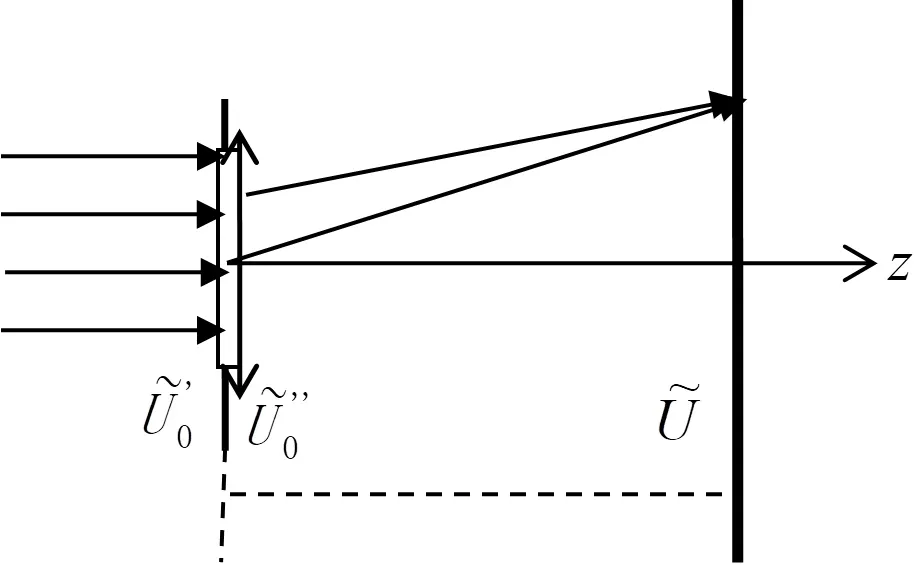
图2 三角形二维周期结构光栅的实验装置
三角形二维周期结构光栅可以采用高精度激光打孔机按设计好的尺寸在薄的不透明材料上生成,然后在光栅后面放置一薄的凸透镜,在薄透镜的焦平面上放接收屏,使衍射屏、透镜、接收屏中心在同一水平直线上,并放置在同一光学导轨上,用一束平行光照射衍射光栅,在接收屏上就能得到三角形二维周期结构光栅的衍射图样,如图3所示。

图3 三角形二维周期结构光栅的衍射图样
2 三角形二维周期结构光栅的衍射场
设三角形二维周期结构光栅和薄的凸透镜所在位置(x0,y0,0),接收屏所在的位置为(x,y,z),如图2所示,则三角形二维周期结构光栅屏函数为:

则薄透镜的变换函数为[1-2]:

其中f为薄透镜的焦距,则三角形二维周期结构光栅和透镜组合在一起的变换函数为:
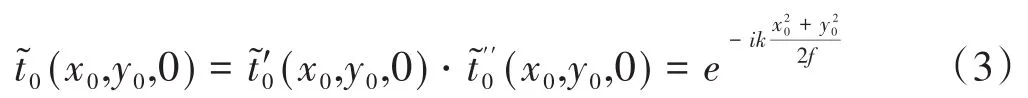
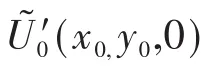

在傍轴条件下,根据基尔霍夫衍射积分式得:
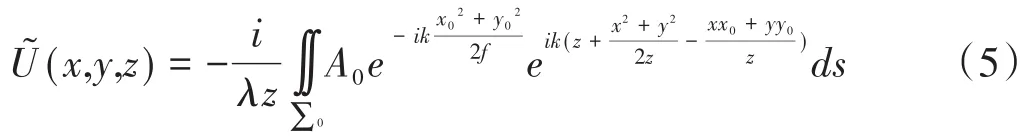
对上式的积分很复杂。这里只研究像面上(z=f)的衍射问题,为了推导简单一些,采用直角三角形全同单元,设直角的边长为a、b。在近轴的条件下,根据基尔霍夫衍射积分式得波前函数为:
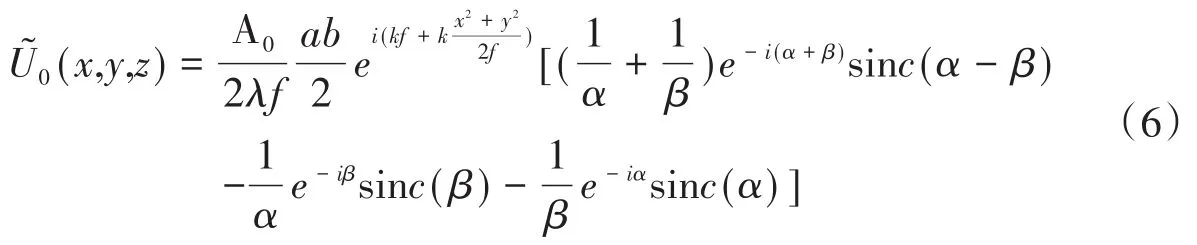
再根据相移-位移定理得第一排,三角形单元沿x轴方向作周期性排列而形成一维光栅衍射场在像面上的波前函数为:
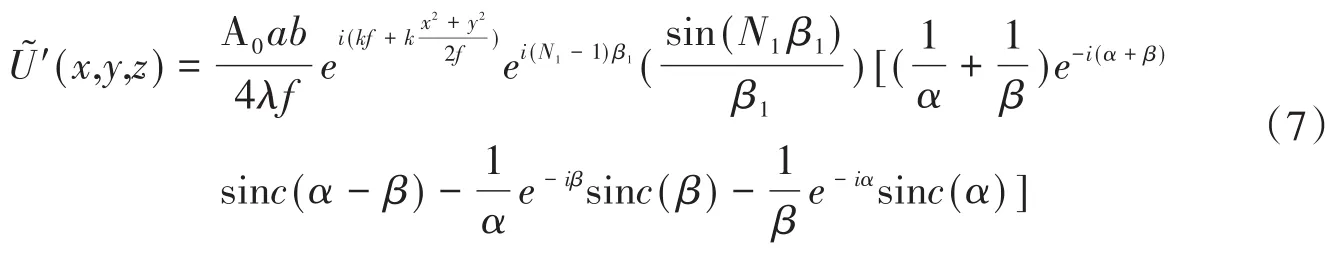
然后把每一排看成一个大单元,大单元沿y轴方向作周期性排列而成为二维光栅,根据位移-相移定理得二维周期结构光栅衍射场在像面上的波前函数为:
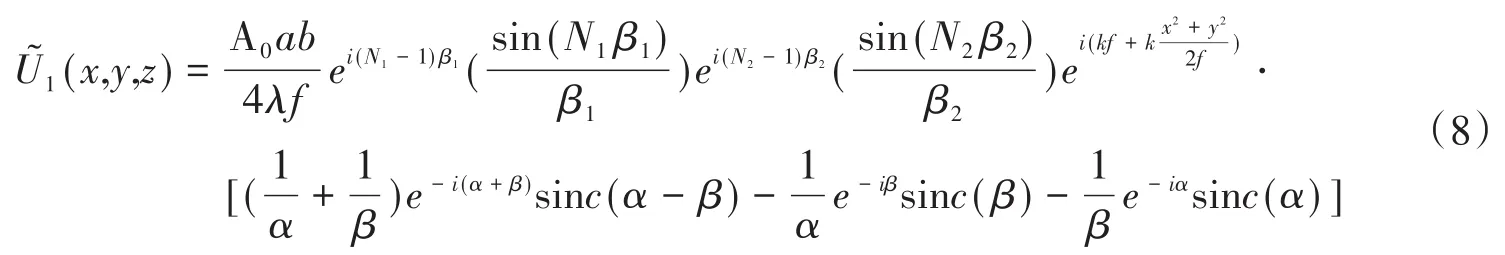
平行光通过三角形二维周期结构光栅在像面上(z=f)衍射波的振幅(取正值)为:
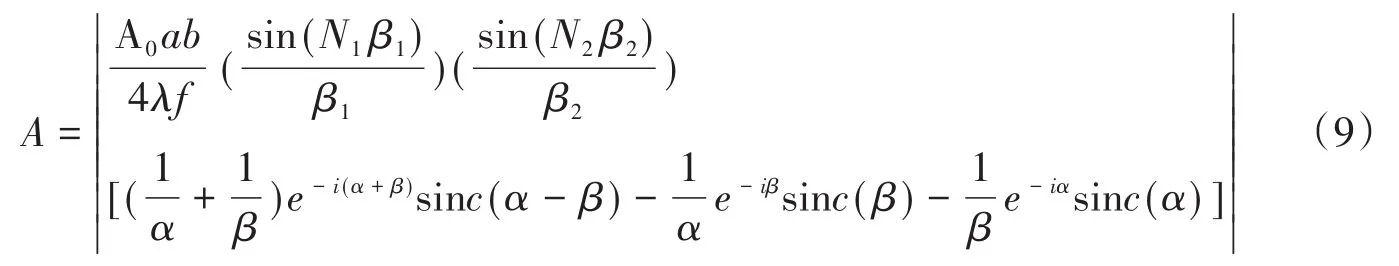
平行光通过三角形二维周期结构光栅在像面上(z=f)衍射波的光强为:
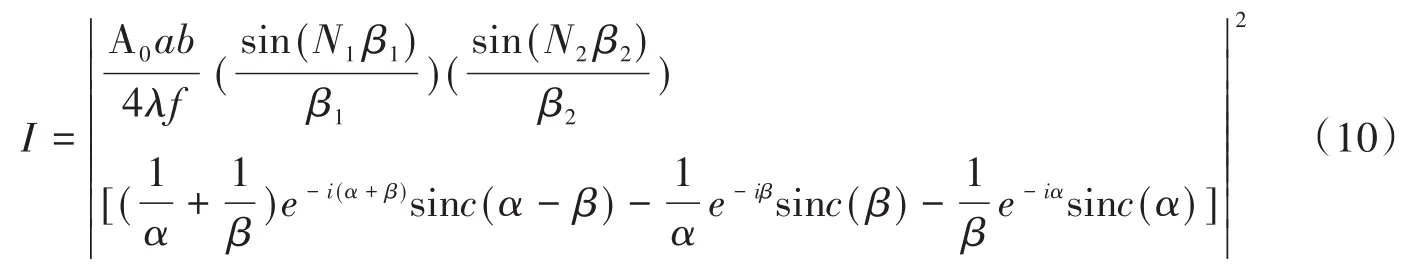
根据(9)、(10)式,利用计算机数据模拟得出平行光通过三角形二维周期结构光栅的衍射波在像面振幅分布和光强分布图样[3]。如图4-图7所示,相关参数取值为:A1=1个单位个单位,λ=632.8nm,a=b=1×10-4m,d1=d2=5×10-4,f=10m,N1×N2=100个全同三角形。
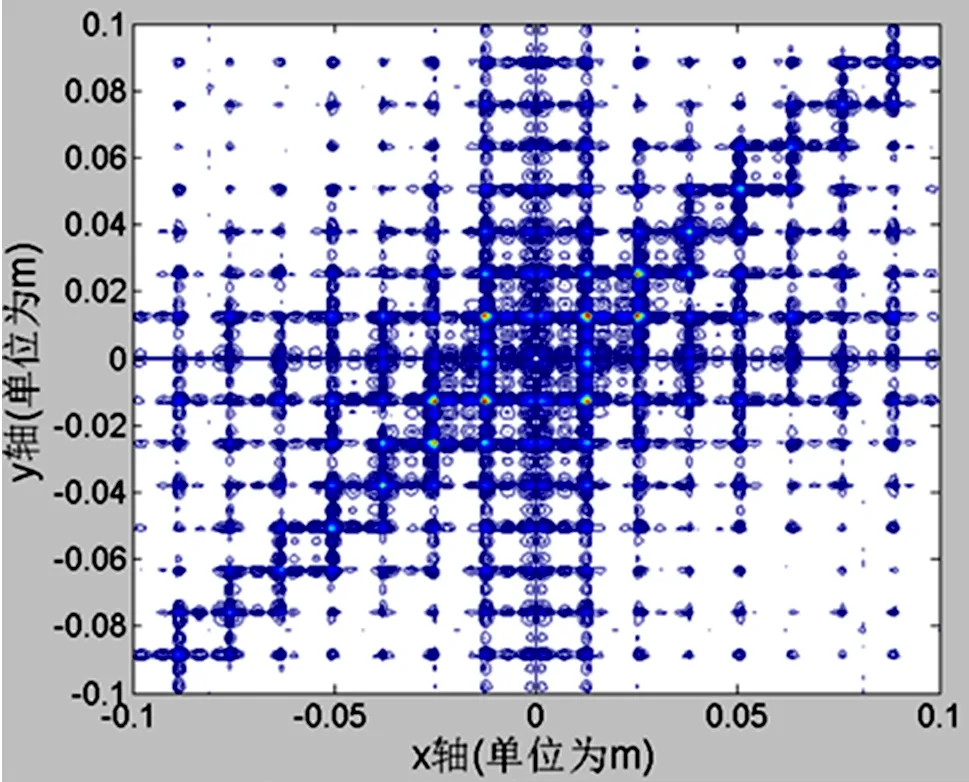
图4 三角形二维周期结构光栅在像面上相对振幅等高线分布图

图5 三角形二维周期结构光栅在像面上相对振幅分布图
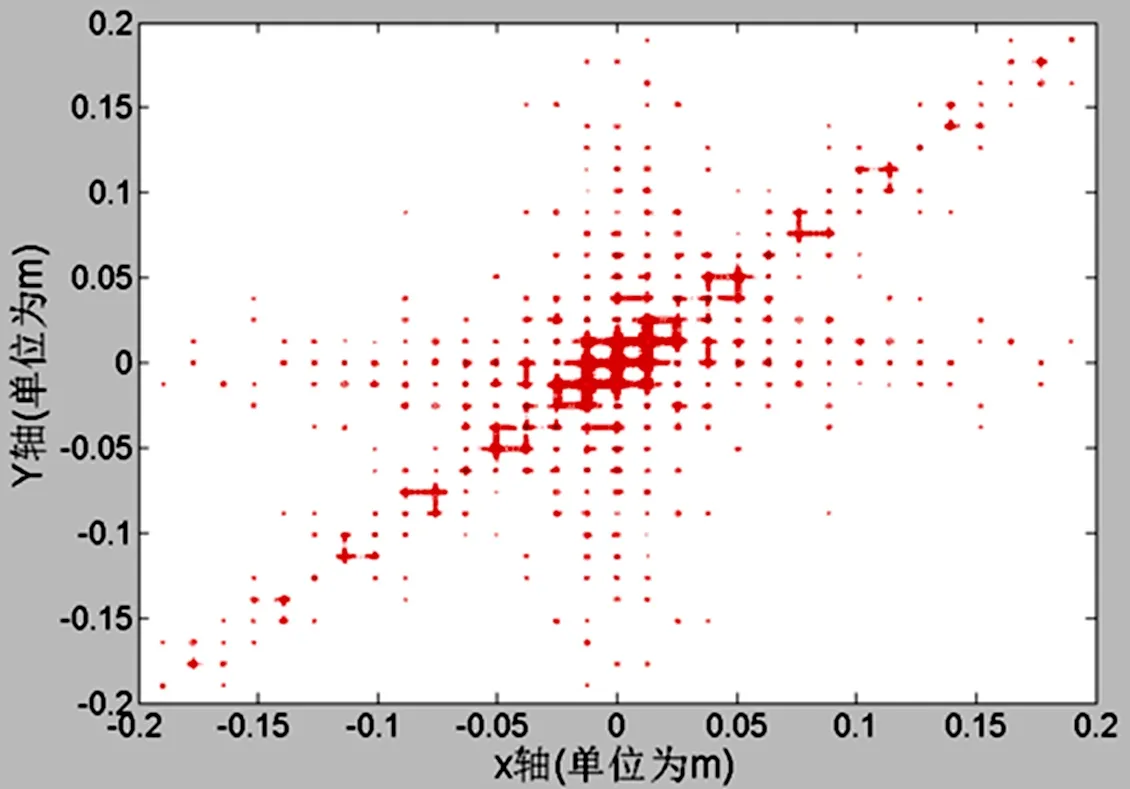
图6 三角形二维周期结构光栅在像面上相对光强等高线分布图
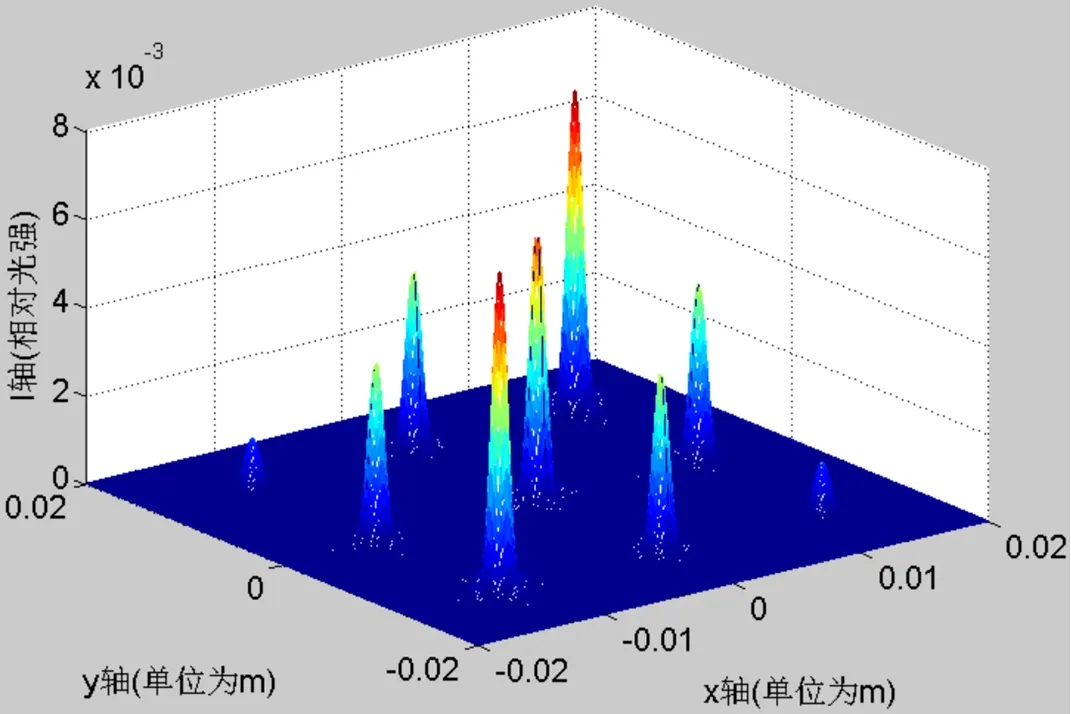
图7 三角形二维周期结构光栅在像面上相对光强分布图
3 结论
从图5和图7可以看出,平行光通过三角形二维周期结构光栅衍的射图样有一系列极强衍射峰,并且在极强衍射峰四周又出现次级衍射峰。
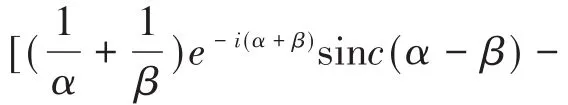
此研究方法和结论可为人们研究物质结构和材料生长的性质特征等提供一种新的研究方法。

