软土地层并行曲线隧道施工顺序对既有隧道的影响

邓 碧，张俊伟，诸葛绪松，刘文献，林星涛，5，6，苏 栋，5，6，陈湘生，5，6

(1. 深圳大学 土木与交通工程学院，广东 深圳 518060； 2. 中铁十五局集团有限公司，上海 200070；3. 珠海大横琴城市新中心发展有限公司，广东 珠海 519030； 4. 珠海市规划设计研究院，广东 珠海 519000;5. 深圳大学 滨海城市韧性基础设施教育部重点实验室，广东 深圳 518060；6. 深圳大学 深圳市地铁地下车站绿色高效智能建造重点实验室，广东 深圳 518060)

0 引 言

为了节约成本和减小地铁隧道对周围建筑物的影响，位于繁华城区下方的地铁隧道施工往往采用平行近接的形式[1]。平行近接隧道由于先后施工的原因，在间距较小情况下，两隧道间的土体间易受到多次扰动，导致后施工的隧道对已建隧道产生较大影响，从而威胁其结构安全。因此开展双线隧道施工顺序影响研究是十分必要的。

针对平行直线隧道施工对周围环境的影响，国内外学者已进行了较为系统的研究，不仅在既有隧道影响[1-2]、地层影响[3-6]等方面取得了丰硕的研究成果，而且对平行隧道施工引起地层沉降的机理进行了深入分析[7]。然而在实际盾构隧道工程中，线路周边环境复杂，为了减小盾构施工扰动造成的影响，常选用曲线盾构方案。部分学者[8-12]通过理论方法对曲线隧道进行了研究：陈剑等[9]基于空间向量分析理论，提出适用于一般三维曲线隧道施工几何参数的理论算法；孙捷城等[10]基于Mindlin解，推导得到曲线盾构施工引起的开挖面附近地表变形计算公式；邓皇适等[11]在前人[8-10]研究的基础上，建立了曲线隧道的地层损失模型，并推导得到了曲线盾构隧道开挖引发地表沉降的计算公式，通过理论方法研究了不同曲率半径、刀盘直径和盾壳长度对地表沉降的影响。但理论方法计算假设众多，且多考虑弹性，有一定局限性。随着计算机技术和数值分析软件的发展，数值计算方法能真实、有效、经济地模拟各种工程及其施工过程，因此得到了广泛应用。陈强[13]针对实际盾构隧道施工中的难题，采用数值模拟、文献调研等方法，提出了针对小曲线半径隧道的设计思路和施工方案；张明聚等[14]通过数值模拟分析了小半径曲线段盾构掘进开挖面稳定情况，并提出了长距离小半径曲线段盾构掘进以及姿态控制措施；梁晗[15]和Zhang等[16]运用数值分析方法，对小曲率曲线隧道开挖引发的地表沉降规律和盾构管片的受力和变形规律进行了研究。然而，现有研究通常着重于分析曲线隧道施工引起的地层沉降和新建隧道管片本身的变形，很少考虑平行曲线隧道施工顺序和曲率半径对既有隧道的影响。

本文以横琴杧洲隧道工程为依托，采用数值模拟方法研究并行曲线隧道曲率半径和施工顺序对既有隧道位移和内力产生的影响。

1 三维有限元建模

1.1 数值模型

本文以横琴杧洲隧道工程为例进行计算。横琴杧洲隧道工程位于横琴一体化区域，采用单层双管盾构隧道方案，泥水盾构施工。盾构隧道外径为14.5 m，内径为13.3 m，管片宽度为2 m，平均埋深为10 m。本项目左右盾构线间距为0.7D(D为隧道外径)。场地土层主要由冲填土、淤泥层与粉质黏土层组成，两隧道位于淤泥层中，地下水位于地表以下约1.5 m。

本文采用PLAXIS 3D有限元软件进行建模，计算模型中隧道埋深取10 m。为了消除边界效应的影响，选取5倍洞径作为边界，即土体高度取70 m，横向土层和纵向土层均选取250 m区域，如图1所示。模型边界条件为：模型四周为水平约束，模型底面为三向约束，顶面为自由面。土体采用实体单元模拟，衬砌采用板单元模拟。

图1 三维有限元模型Fig.1 Three-dimensional Finite Element Model

1.2 计算参数选取

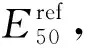
表1 HSS模型计算参数Table 1 Calculation Parameters of HSS Model

隧道衬砌采用C60混凝土，其弹性模量为36.5 GPa，泊松比为0.167。考虑隧道衬砌环向和纵向接缝对刚度的削弱作用，环向衬砌的有效模量取衬砌弹性模量的0.7倍[19]，在不考虑螺栓预紧力的情况下，纵向有效模量取衬砌弹性模量的0.1倍[20]，即隧道衬砌的环向和纵向弹性模量实际取值为25.55 GPa和3.65 GPa。

1.3 盾构机掘进模拟

首先对既有隧道进行开挖，通过冻结既有隧道区域的土体和激活该区域的衬砌来模拟既有隧道开挖。既有隧道开挖完成后，将位移清零，再模拟新建隧道开挖过程。通过冻结已开挖的土体，激活相应区域的衬砌和当前开挖面的支护压力来模拟盾构机的开挖。由于泥水盾构的支护压力大于外界水土压力，取开挖面的支护压力为2.5P(隧道轴线处的初始水平应力P=249.90 kPa)，压力作用在隧道轴线处，沿深度方向线性增加，梯度均为14.7 kPa·m-1。

2 计算结果分析

为了研究并行曲线隧道施工时，曲率半径和施工顺序对既有隧道的影响，采用PLAXIS 3D有限元软件，建立2种不同半径的盾构隧道模型，曲率半径r分别为500 m和800 m。每个模型分别在2种不同施工顺序下进行计算：外侧隧道先开挖，内侧隧道盾构施工对外侧隧道的影响；内侧隧道先开挖，外侧隧道盾构施工对内侧隧道的影响。通过研究不同曲率半径和不同施工顺序作用下的既有隧道受力变形规律，为并行曲线隧道的施工提供参考。

本文共讨论4个工况：曲率半径为500 m时，外侧隧道先开挖(工况1)和内侧隧道先开挖(工况2)；曲率半径为800 m时，外侧隧道先开挖(工况3)和内侧隧道先开挖(工况4)。为了减少边界效应的影响，研究新建隧道开挖一半时对既有隧道的影响，取既有隧道的3个截面作为观测面，如图2所示。

图2 新建隧道与既有隧道位置关系Fig.2 Location Relationship Between New Tunnel and Existing Tunnel

2.1 隧道结构位移

图3为不同施工顺序下既有隧道的结构位移云图。由图3可知，既有隧道靠近新建隧道一侧的位移变化最为明显。既有隧道最大位移在盾构开挖面前方约10 m(0.7D)位置处，如图4所示。在工况1，2，3，4中，对应既有隧道的最大位移分别为12.42，11.84，14.25，13.83 mm，远小于隧道设计验算要求的0.3%D(43.5 mm)，未超过隧道设计变形指标。由上述分析可知，当隧道曲率半径为800 m和500 m时，外侧隧道开挖引起的既有隧道位移略小于内侧隧道开挖。施工顺序对既有隧道结构位移的影响较小。随着曲率半径(r=500～800 m)的增加，既有隧道位移增大了约15%(分别从工况1的12.42 mm增加到工况3的14.25 mm，从工况2的11.84 mm增加到工况4的13.83 mm)，这表明曲率半径对既有隧道位移影响相对较大。既有隧道的位移主要在盾构开挖面前方2.5D、后方1D范围内产生，建议平行隧道施工时特别关注此范围内既有隧道的响应，必要时针对该区域进行局部加固处理，以确保地铁运营安全。

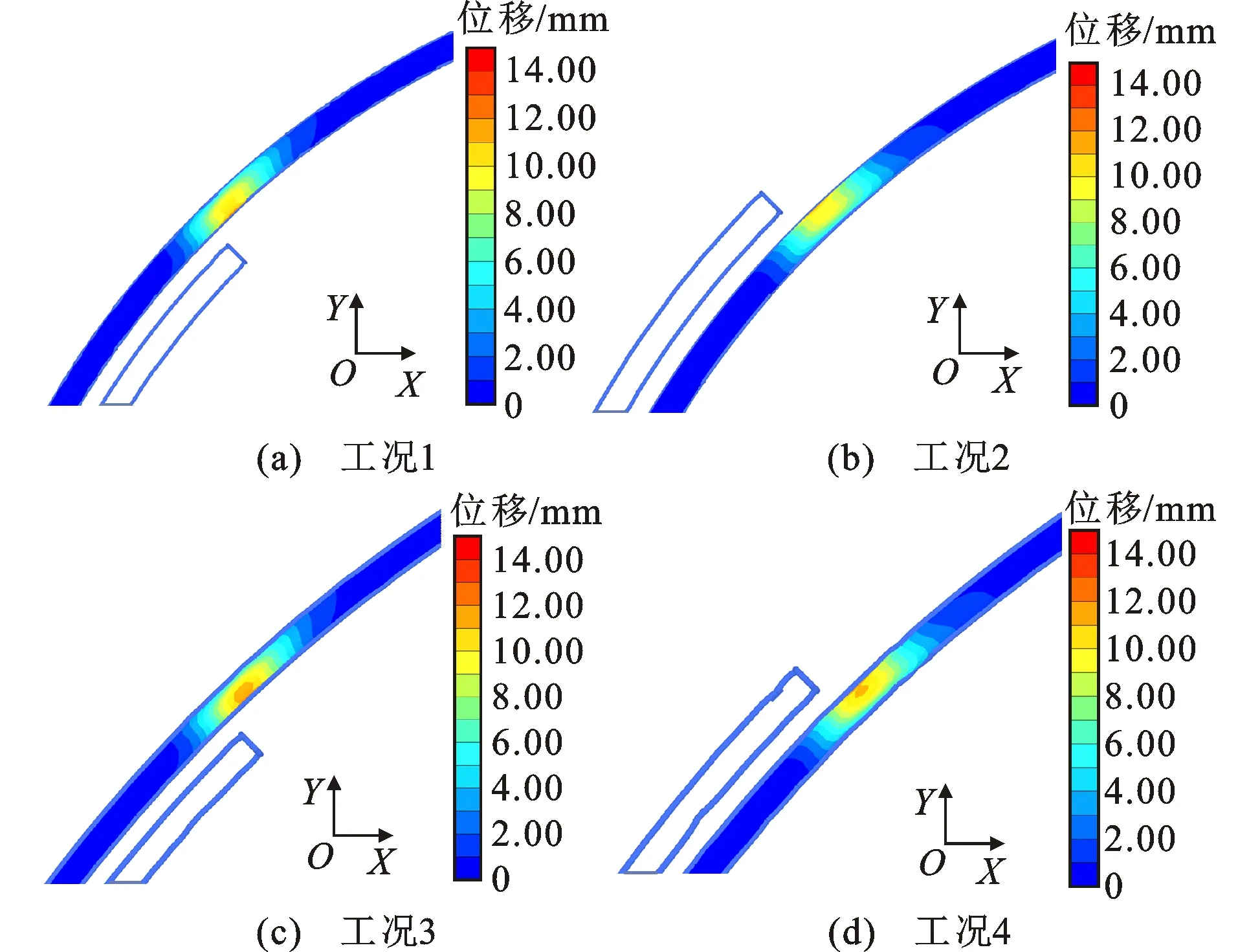
图3 既有隧道空间结构位移云图Fig.3 Displacement Nephogram of Spatial Structure of Existing Tunnel

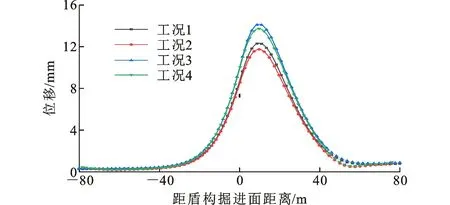
图4 既有隧道位移Fig.4 Displacement of Existing Tunnel

2.2 隧道结构内力

2.2.1 曲率半径为500 m时既有隧道弯矩分布

图5为工况1，2的既有隧道弯矩分布云图。图6为工况1，2的6个剖面的弯矩分布图，规定外侧受拉内侧受压为正，反之则为负。工况1，2的6个横剖面位置如图2所示，各剖面间距为10 m。为便于对结果进行描述，选定沿掘进方向观察，隧道右拱腰为0°，顶部为90°，左拱腰为180°，底部为270°。

图5 既有隧道弯矩云图Fig.5 Bending Moment Nephograms of Existing Tunnel

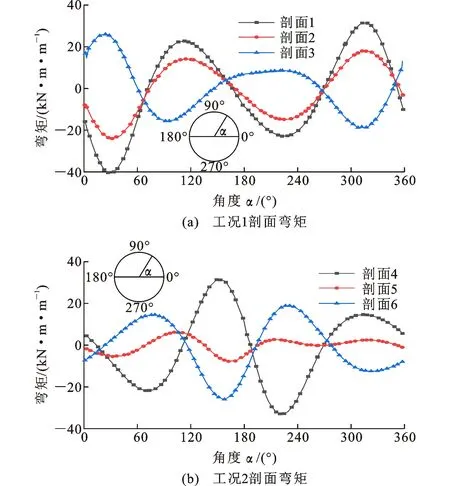
图6 既有隧道剖面弯矩Fig.6 Bending Moments of Existing Tunnel Section

由图5(a)和图6(a)可知，在工况1中，3个剖面最大弯矩和最小弯矩分别为31.7 kN·m·m-1和-40.34 kN·m·m-1，其分别位于剖面1的313°和30°位置。剖面1、剖面2的弯矩变化趋势相似，剖面右侧(350°到70°)和左侧(170°到270°)产生了较大的负弯矩，顶部和底部产生了较大的正弯矩。剖面3与前两者相反，剖面右侧和左侧产生了较大的正弯矩，顶部和底部产生了较大的负弯矩。

由图5(b)和图6(b)可知，在工况2中，3个剖面最大弯矩和最小弯矩分别为31.53 kN·m·m-1和-33 kN·m·m-1，其分别位于剖面4的150°和220°位置。剖面4的弯矩变化趋势为：剖面右侧(270°到15°)和左侧(110°到190°)产生了较大的正弯矩，顶部和底部产生了较大的负弯矩。剖面5产生的弯矩相对较小。剖面6与剖面4相反，剖面右侧和左侧产生了较大的负弯矩，顶部和底部产生了较大的正弯矩。由此可知，离盾构开挖面最近的既有隧道剖面产生的弯矩最大，且最大和最小弯矩位置均出现在紧邻新建隧道一侧。由于工况2中既有隧道的弯矩(绝对值)更小，因此内侧隧道先开挖更安全。

2.2.2 曲率半径为500 m时既有隧道轴力分布

图7为工况1，2的既有隧道轴力分布云图，图8为既有隧道顶部、底部和拱腰4个位置处沿纵向的轴力分布，规定受拉为正，受压为负。

图7 既有隧道轴力云图Fig.7 Axial Force Nephograms of Existing Tunnel

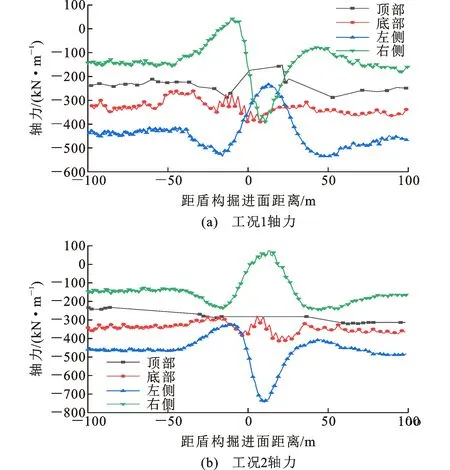
图8 既有隧道轴力Fig.8 Axial Forces of Existing Tunnel

由图7，8可知，在工况1中，受盾构开挖影响，在盾构开挖面前方2D、后方0.5D范围内，既有隧道顶部和左侧拱腰处轴力(绝对值)减小；在盾构开挖面后方0.35D～1.15D范围内，既有隧道右侧拱腰出现拉力最大值42.02 kN·m-1，在盾构开挖面前方2D范围内，轴力(绝对值)增大；既有隧道底部受到影响较小。在工况2中，受盾构开挖影响，在盾构开挖面前方2D范围内，既有隧道左侧拱腰轴力增大；在盾构开挖面后方1.25D范围内，既有隧道右侧拱腰出现拉力最大值73.8 kN·m-1；既有隧道顶部和底部受到影响较小。隧道抗拉能力较弱，建议并行曲线隧道施工时，特别关注既有外侧隧道右侧盾构开挖面后方0.35D～1.15D范围和既有内侧隧道右侧盾构开挖面后方1.25D范围的受拉区域。

2.2.3 曲率半径为800 m时既有隧道内力分布

图9为工况3，4弯矩与轴力分布云图。由图9可知，在2个工况中，离盾构开挖面最近的既有隧道剖面产生的弯矩最大，且最大和最小弯矩均出现在靠近新隧道一侧。在盾构开挖面前方一定距离内既有隧道产生的轴力最大。施工顺序对既有隧道剖面内力影响较小，这是因为此工况中隧道直径为14.5 m，曲率半径为800 m，近似于直线隧道。曲率半径为800 m时可不考虑施工顺序的影响。本文中4个工况下既有隧道的弯矩和轴力都远小于原设计弯矩(212 kN·m·m-1)和设计轴力(3 473.92 kN·m-1)，不会导致隧道的破坏。

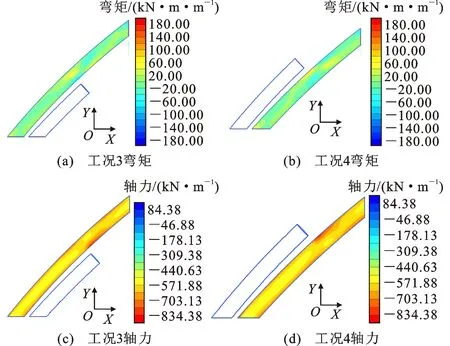
图9 既有隧道内力云图Fig.9 Internal Force Nephograms of Existing Tunnel

3 结 语

(1)既有隧道的位移主要在盾构开挖面前方2.5D、后方1D范围内产生，既有隧道最大位移在盾构开挖面前方约10 m(0.7D)的位置处。建议平行隧道施工时特别关注此范围内既有隧道的响应，必要时针对该区域进行局部加固处理，以确保地铁运营安全。施工顺序对既有隧道位移影响较小，曲率半径对既有隧道位移影响较大，随着曲率半径(r=500～800 m)的增加，既有隧道位移增加约15%。

(2)曲率半径为500 m时，施工顺序对既有隧道弯矩变化趋势影响较小，离盾构开挖面最近的既有隧道剖面产生的弯矩最大，且最大和最小弯矩均出现在靠近新隧道一侧。内侧隧道先开挖时，既有隧道的弯矩(绝对值)更小，内侧隧道先开挖更安全。施工顺序对既有隧道轴力变化趋势影响较大，既有隧道左侧和右侧受到盾构掘进影响较明显。外侧隧道先开挖时，既有隧道左侧轴力绝对值减小，右侧盾构开挖面后侧出现拉力，前侧轴力绝对值增大；内侧隧道先开挖时，既有隧道左侧轴力绝对值增大，右侧盾构开挖面前侧出现拉力。

(3)曲线隧道半径为800 m时，双线隧道近似于平行隧道，施工顺序对既有隧道内力影响较小，可不考虑施工顺序的影响。