不同细骨料下不锈钢管混凝土构件受弯性能研究
张伟杰,廖飞宇,侯 超,任 彧,谈建俊,任梦璐
(1. 福建农林大学交通与土木工程学院,福建,福州 350108;2. 南方科技大学海洋科学与工程系,广东,深圳 518055;3. 福建建工装配式建筑研究院有限公司,福建,福州 350001)
近三十年来我国迅速发展的土木工程基础建设产生了巨量的混凝土需求与有限的自然资源之间的矛盾[1-2],作为混凝土主要原材料之一的河砂由于过度开采已经造成严重的生态问题[3]。随着发展海洋经济,建设海洋强国战略的实施,海砂作为一种储量丰富的资源,具有粒性优良、含泥量低等特点[4],有望成为河砂潜在的替代品[5]。Guo等[6]、Limeira 等[7]、刘伟等[8]和黄亮等[9]的研究结果表明:海砂替代河砂并不会对混凝土的受压强度和耐久性造成明显的影响。
文献[10]提出了钢材与混凝土界面发生腐蚀所需具备的三个条件,若将海砂混凝土置于密闭的钢管中,可阻碍氯离子与钢材反应所需的水和氧,从而阻断腐蚀反应路径。查晓雄等[11]利用试验和数值分析的方法证明了海砂混凝土不会对钢管产生很大的腐蚀作用,可应用于钢管中,形成钢管海砂混凝土组合构件。为了进一步降低海砂对钢管的腐蚀风险,可将海砂混凝土灌注于与比普通钢管相比抗腐蚀性能更强的不锈钢管中,形成不锈钢管海砂混凝土组合构件[12]。
不锈钢管混凝土结构兼具了普通钢管混凝土良好的力学性能和不锈钢优越的耐久性和抗腐蚀性等特点[13-14]。因其灌注了混凝土,工程造价得到相对降低[15],应用于海洋平台、高层建筑和桥梁等工程中时,后期维护成本亦得到降低[16]。Han等[13]和廖飞宇等[14]对比了不锈钢和普通碳素钢材料力学性能并对约束效应系数相同的不锈钢管混凝土和普通钢管混凝土在轴心受压荷载作用下的荷载-变形关系曲线进行了比较,比较结果表明:在受荷后期,较普通钢管混凝土而言,不锈钢对核心混凝土的约束进一步放大,轴压承载力高。汪良滨[16]比较了同规格的不锈钢管混凝土和普通钢管混凝土受弯力学性能,结果同样表明:在受荷后期,不锈钢管混凝土受弯构件较普通钢管混凝土受弯构件,受弯承载力高。此外,代鹏等[17]、Uy 等[18]、陈鑫等[19]和Pantha 等[20]将不锈钢管混凝土轴压、压弯承载力试验值与现行的钢管混凝土结构规范或规程计算值进行了比较,结果表明:规范或规程的计算值均偏于保守,主要是由于未对不锈钢显著的后期强化特性予以考虑。
目前,不锈钢管混凝土已被应用在中国香港的昂船洲大桥(近海大桥)和纽约赫斯特大厦等实际工程中[14]。有关不锈钢管混凝土抗弯性能的研究见陈誉等[21-22]报道了圆形和方形两种截面形状的不锈钢管普通混凝土在弯曲荷载作用下的试验研究,而有关不同细骨料种类(原状海砂、淡化海砂和普通河砂)对不锈钢管混凝土力学性能影响的报道仅见轴心受压工况[1,23]。
为探寻海砂替代河砂形成不锈钢管海砂混凝土组合结构的可能性,缓解河砂资源紧缺和发挥就地取材优势,促进其在近海工程建设中的应用。本文对3 种不同细骨料形成的不锈钢管混凝土受弯力学性能开展了试验研究,考察了不同截面形状和剪跨比下细骨料种类对不锈钢管混凝土构件受弯性能的影响。考虑不锈钢显著的后期应变强化特性,为不锈钢管混凝土合理设计提供必要的依据,建立了圆形和方形不锈钢管混凝土纯弯构件的有限元模型,并在参数分析的基础上建议了不锈钢管混凝土受弯承载力计算的简化公式,可为研究不锈钢管混凝土压弯性能并确定轴力-弯矩相关曲线提供参考。
1 试验概况
1.1 试验设计和制作
共进行24 个不锈钢管混凝土试件在纯弯作用下的力学性能试验研究,其中不锈钢管原状海砂混凝土、不锈钢管淡化海砂混凝土和不锈钢管普通河砂混凝土各8 个。试验主要参数为:细骨料类型(原状海砂、淡化海砂、普通河砂)、截面形状(圆形、方形)和剪跨比(λ=1.75、3.5)。试件截面外直径D或外边长B均为127 mm,不锈钢管壁厚ts均为2.88 mm,试件的参数详见表1。其中,L为试件长度;L0为试件有效长度;fcu为核心混凝土立方体抗压强度;λ(λ=a/D或λ=a/B,a为支座边缘到四分点集中荷载作用处的距离,D为圆形试件外直径,B为方形试件外边长)为试件剪跨比;Mue为试件受弯承载力;Ki、Ks分别为试件实测弯矩与曲率关系曲线计算所得的的初始阶段抗弯刚度和使用阶段抗弯刚度。试件钢管采用冷弯不锈钢管,端板为为160 mm×160 mm×10 mm 方形截面,试件制作过程参考文献[23]。

表1 试件信息表Table 1 Details of specimens
1.2 材料性能
试件所用的不锈钢管为奥氏体型304L 级,按照《金属材料拉伸试验 第1 部分:室温试验方法》(GB/T 228.1-2010)[24]中标准试验方法进行了3 个标准不锈钢试件拉伸试验,各项材料性能见表2,其中,σ0.2为产生0.2%塑性变形所对应的应力(屈服强度),ν为泊松比,Es为弹性模量,n为不锈钢材料应变硬化指数[25]。可见经过冷弯工艺而成的不锈钢管,弯角区域的屈服强度较平板区域得到显著提高[26]。

表2 不锈钢材性试验结果Table 2 Tensile test results of the stainless steel
核心混凝土所用的细骨料类型分别为原状海砂、淡化海砂和普通河砂,原状海砂为取自于福建省福州市长乐区近海区域的天然海沙,细度模数为2.5,较河砂粒径小,但硬度大。淡化海砂按照文献[23]中的淡水冲洗法对原状海砂浸泡、晾晒和筛分得到,经过淡化后的海砂,氯盐、硫酸盐和贝壳等杂质含量均降低,但使其制备而成的混凝土成本提高5%~10%[23]。试验所用的3 种细骨料如图1 所示,海砂中含有肉眼可见的贝壳。

图1 核心混凝土中所用的三种细骨料类型Fig. 1 Three types of fine aggregates used in core concrete
按照《建筑用砂》(GB/T 14684-2011)[27]中建议的硝酸银滴定法测定了3 种细骨料氯离子含量,结果列于表3。由表可见,原状海砂的氯离子含量最高为0.063%;淡化海砂中氯离子含量为0.018%,低于《海砂混凝土应用技术规范》(JGJ 206-2010)[28]中规定的限值0.03%;普通河砂中氯离子含量为0.006%。所有试件的核心混凝土均为自密实混凝土,其质量配合比均为:mPO42.5水泥∶m水∶m细骨料∶m粗骨料∶m粉煤灰∶m减水剂=263.73 kg/m3∶187.25 kg/m3∶759.94 kg/m3∶1013.26 kg/m3∶175.82 kg/m3∶4.395 kg/m3,其中粗骨料采用最大粒径为20 mm 的花岗岩碎石,粉煤灰为Ⅱ级粉煤灰,减水剂采用TW-PS 高效缓凝减水剂。保持水泥、水、粗骨料、粉煤灰及减水剂完全相同,等量替换不同种类的细骨料,试验时测得的与核心混凝土同条件养护下的立方体试块(150 mm×150 mm×150 mm)的抗压强度fcu、棱柱体试块(150 mm×150 mm×300 mm)的弹性模量Ec和其他混凝土材料性能见表3,可见试验时原状海砂混凝土和普通河砂混凝土强度分别为44.3 MPa 和44.0 MPa,二者强度基本相当,淡化海砂混凝土强度最高,为45.3 MPa。

表3 混凝土材性试验结果Table 3 Material test results of the core concrete
1.3 加载制度与测点布置
试验加载装置如图2 所示,试件所受的集中荷载由50 t 液压千斤顶施加,加载过程中的荷载实时数据由1000 kN 荷载传感器进行监测。试验采用四分点加载方式,两加载点之间为纯弯段。试验采用分级加载制:初始阶段,每级荷载为预估极限荷载的1/10;当不锈钢管拉区纵向应变测点达到屈服后,每级荷载转为预估极限荷载的1/15,持荷时间均为2 min;接近预估极限荷载时采用慢速连续加载,直至跨中挠度达到计算跨度的1/10 或者试件出现明显的破坏现象(焊缝开裂、大变形)时停止加载。

图2 试验装置示意图 /mmFig. 2 Schematic view of the test setup
在支座、四分点加载和跨中截面处共设置了5 个位移计(LVDT)以准确测得试件在加载过程中挠度变化;在纯弯段架设了1 个曲率仪以量测加载过程中试件曲率的发展,曲率仪的原理参考文献[16];在试件跨中截面处每间隔90°位置贴置横、纵向应变计各1 个,共计8 个应变计,以获得在加载过程中试件跨中截面处外不锈钢管应变数据。加载过程中的荷载和变形数据均由数据采集系统(IMC)自动采集。
2 试验结果及其分析
2.1 破坏形态
图3 所示为剪跨比λ 为1.75 的试件整体破坏模态。可见,试件的整体破坏模态并无因核心混凝土细骨料种类的不同而有显著改变,圆形试件不锈钢管屈曲程度不明显,方形截面试件受压区不锈钢管局部鼓曲程度显著,且波浪形鼓曲在纯弯段基本上对称分布,二者整体上均有明显的挠曲变形。整体而言,所有试件均延性良好,表现出较好的变形能力。典型试件核心混凝土破坏模态如图4 所示,可见核心混凝土受拉区均出现裂缝。对比图4(a)与图4(b)可知:在同一剪跨比(λ=3.5)下圆形试件,原状海砂核心混凝土受拉区裂缝较普通河砂核心混凝土数量多、宽度大、分布范围广,甚至部分裂缝贯穿至中性轴以上,这主要是由于原状海砂中含有一定量贝壳及其他轻质杂质,更易导致裂缝的生成与发展;对比图4(a)与图4(c)可知:在同一剪跨比(λ=3.5)下,细骨料种类为原状海砂的核心混凝土,方形试件较圆形试件受拉区混凝土裂缝更多更密集,值得注意的是,方形试件受压区钢管鼓曲处,混凝土被压溃,这与细骨料种类为普通河砂的核心混凝土的方形试件与圆形试件比对情况类似。

图3 试件破坏模态对比Fig. 3 Comparison of failure modes of the tested specimens

图4 典型试件核心混凝土破坏模态Fig. 4 Failure modes of core concrete in typical specimens
2.2 弯矩-跨中挠度关系曲线
三种不同细骨料种类的不锈钢管混凝土在弯曲荷载作用下的弯矩M-跨中挠度um关系曲线如图5 所示,可见实测的3 种不同细骨种类的不锈钢管混凝土构件在纯弯作用下的M-um关系曲线形状相似,均可划分为弹性段、弹塑性段和强化段。弹性段:试件整体无明显的变形,跨中挠度发展十分缓慢,钢管和核心混凝土间的相互作用力较小,二者单独承担荷载,弯矩与跨中挠度呈线性增长,弯矩的增长速率明显大于跨中挠度的增长速率;弹塑性段:当跨中受拉区外不锈钢管屈服时,M-um曲线由线性增长转入非线性增长,中和轴的位置不断向受压侧移动,截面受拉区范围不断扩大;强化段:试件变形明显增大,挠度的增长的速率大于弯矩的增长速率,当跨中挠度达到L0/10 时,各试件承载力也无下降,说明不锈钢管原状海砂混凝土、不锈钢管淡化海砂混凝土和不锈钢管普通河砂混凝土三者均具有良好延性,不锈钢管对核心混凝土约束作用可减小海砂中贝壳和其他轻质杂质对试件力学性能的影响。

图5 试件弯矩-挠度曲线Fig. 5 Bending moment-deflection curves of the tested specimens
参考文献[29],对于M-um无下降段的曲线,可取试件跨中截面受拉区钢管最大纤维应变达到10 000 με 时对应的弯矩值为试件极限弯矩Mue,各个试件的Mue列于表1。需要说明的是,编号为C-SS-3.5-B 试件在达到极限荷载前其端板和钢管焊缝开裂,因此无法得到其极限抗弯承载力。
2.3 弯矩-曲率关系曲线
利用架设在试件纯弯段的曲率仪记录的数据,绘制了典型试件的弯矩M-曲率 φ关系曲线,如图6 所示。可见,在其他参数相同的情况下,不锈钢管原状海砂混凝土、不锈钢管淡化海砂混凝土和不锈钢管普通河砂混凝土试件的M- φ曲线较为接近。参考文献[29 - 30],取M为0.2Mue和0.6Mue对应的曲线的割线刚度作为各试件的初始阶段抗弯刚度Ki和使用阶段抗弯刚度Ks,各刚度值均列于表1 中。

图6 弯矩-曲率关系曲线 (λ=3.5)Fig. 6 Bending moment-curvature curves (λ=3.5)
2.4 挠度曲线
图7 为典型圆形不锈钢管原状海砂混凝土和不锈钢管淡化海砂混凝土试件在加载过程中挠度沿试件长度分布情况,图中横坐标为各测点距左端铰支座的距离,即有效长度L0,纵坐标为试件加载过程中不同位置处的挠度值f,实线为实测试件挠曲线,虚线正弦半波曲线,可见,与不锈锈钢管河砂混凝土挠曲线类似,不锈钢管海砂混凝土实测挠曲线与对应的正弦半波曲线均较为吻合,不因核心混凝土细骨料种类的改变而有明显变化。

图7 典型试件挠曲线(λ=3.5)Fig. 7 Distribution of the deflection curves in typical specimens
2.5 截面应变发展
图8 为典型不锈钢管海砂混凝土试件在荷载上升阶段及峰值荷载时中截面不同位置测点纵向应变εsl与截面高度H的关系曲线,横坐标为中截面各个测点纵向应变值,拉应变为正值,压应变为负值,纵坐标为中截面各测点距截面形心轴的距离。需要说明的是,纵坐标值为0 时的纵向应变值为中截面两侧面中点处纵向应变平均值。可见,与不锈钢管河砂混凝土试件类似,加载至峰值荷载过程中,各测点纵向应变连线保持直线,变形符合平截面假定,而对于中和轴,在试件的加载初始阶段,中和轴基本上与截面的形心轴重合,随着荷载的不断增加,由于拉区混凝土逐渐开裂并退出工作,中和轴不断向受压区移动,方形试件截面应变发展规律与圆形试件类似。
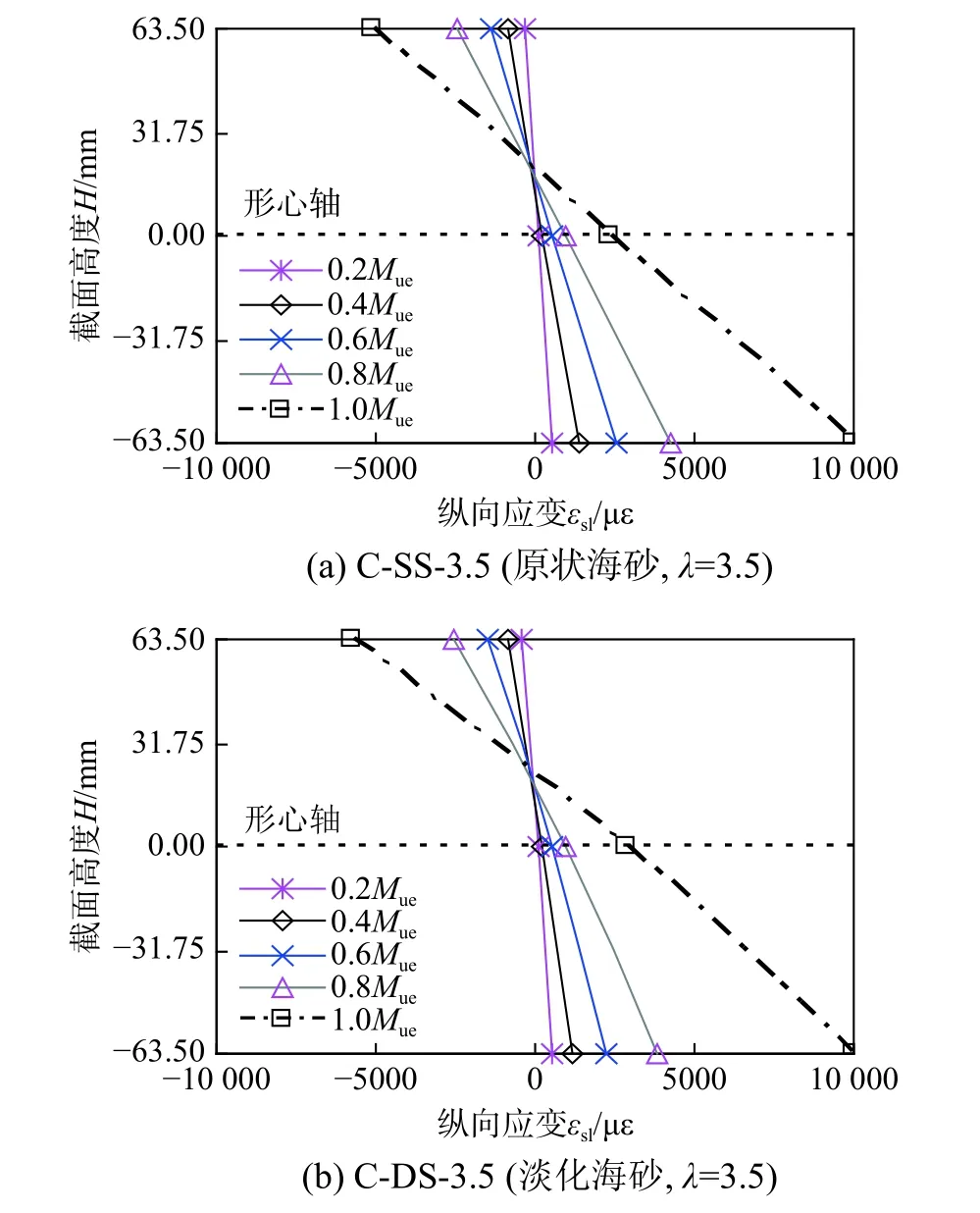
图8 典型试件跨中截面纵向应变分布Fig. 8 Longitudinal strain distribution at the mid-span of typical specimens
2.6 弯矩-应变关系曲线
图9 分别给出了典型的3 种不同细骨料圆形和方形试件在加载过程中实测的弯矩M与试件跨中位置受拉区和受压区钢材纵向应变εsl关系曲线,取拉应变为正值,压应变为负值。图9 中的每一图分别比较了相同参数下不同细骨料种类的试件受压区和受拉区外钢管纵向应变随弯矩值的发展情况,可见,在其他参数相同的情况下,不锈钢管原状海砂混凝土、不锈钢管淡化海砂混凝土和不锈钢普通河砂混凝土试件的M-εsl曲线基本吻合,加载初期,受拉区和受压区外钢管纵向应变均随着弯矩的增大的而增大且呈线性发展,受拉区应变增长速率较受压区应变快,先达到钢材屈服应变εsy,之后随着弯矩值继续增大,受压区应变也达到钢材屈服应变。

图9 试件弯矩-纵向应变关系曲线 (λ=3.5)Fig. 9 Bending moment-top (bottom) Longitudinal strain curves (λ=3.5)
2.7 受弯承载力和抗弯刚度
表1 给出了不锈钢管原状海砂混凝土、不锈钢管淡化海砂混凝土和不锈钢管普通河砂混凝土纯弯试件受弯承载力Mue、初始阶段抗弯刚度Ki和使用阶段抗弯刚度Ks值。可见,方形试件的Mue、Ki和Ks值均大于对应的圆形试件,这是由于方形试件的截面面积大于圆形试件。承载力方面:对于圆形试件而言,无论细骨料种类,剪跨比λ 为3.5 的试件受弯承载力Mue较λ 为1.75 的试件均有所降低,其中原状海砂试件、淡化海砂试件和普通河砂试件的降幅分别为12.0%、5.1%和2.2%,可见,剪跨比对原状海砂圆形试件的受弯承载力的影响相对于其他两种细骨料试件较大;对于方形试件而言:对于不同细骨料种类,剪跨比λ 为1.75 的试件的Mue与λ 为3.5 的试件基本接近。抗弯刚度方面:无论是圆形试件还是方形试件,剪跨比对三种细骨料试件的Ki影响有限,但对Ks的影响较大:λ 为1.75 的试件较λ 为3.5 的试件,其Ks均有不同程度提高,圆形试件Ks增幅为5.2%~29.0%,方形试件的Ks增幅在9.7%~13.1%之间。
为了进一步探究用原状海砂和净化海沙代替普通河砂对不锈钢管混凝土受弯试件受弯承载力和抗弯刚度的影响,分别定义了承载力系数SI1、初始阶段刚度系数FI1和使用阶段刚度系数FI2如下:
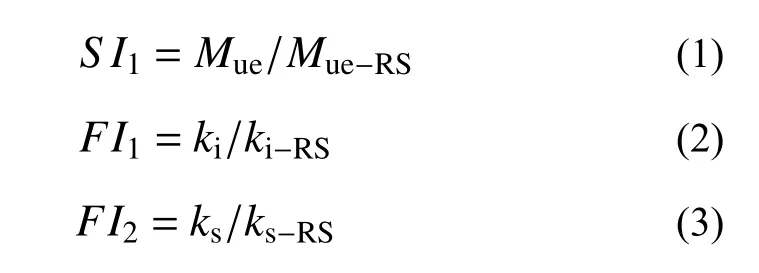
式中:Mue表示试验参数相同的2 根试件受弯承载力的平均值,Mue-RS表示相同试验参数下2 根普通河砂试件受弯承载力的平均值;ki为试验参数相同的2 根试件初始阶段抗弯刚度的平均值,ki-RS表示相同试验参数下2 根普通河砂试件初始阶段抗弯刚度的平均值;ks为试验参数相同的2 根试件使用阶段抗弯刚度的平均值,ks-RS表示相同试验参数下2 根普通河砂试件使用阶段抗弯刚度的平均值。
图10 比较了不同细骨料试件的承载力系数S11,可见,对于圆形构件:在剪跨比λ 为1.75时,原状海砂试件和淡化海砂试件的受弯承载力较普通河砂试件均有所提高,增幅分别为7.4%和1.5%;在λ 为3.50 时,不同细骨料种类试件的承载力系数基本接近。对于方形试件:在剪跨比λ 为1.75 时,细骨料为淡化海砂的试件受弯承载力与普通河砂的试件相近,原状海砂试件较普通河砂试件受弯承载力提高3.9%;在λ 为3.5 时,无论是原状海砂试件还是淡化海砂试件受弯承载力均与普通河砂试件相近。综上,无论是圆形还是方形试件,总体上采用原状海砂和淡化海砂替代普通河砂,对不锈钢管混凝土受弯承载力的影响较小。

图10 不同细骨料对试件承载力的影响Fig. 10 Effects of different fine aggregate types on the flexural resistance of specimens
图11 比较了不同细骨料试件的初始阶段抗弯刚度系数F11,可见,细骨料种类的改变对各试件的初始抗弯刚度影响较小,普通河砂被原状海砂和淡化海砂取代后,不锈钢管混凝土试件的初始阶段抗弯刚度基本相近。

图11 不同细骨料对试件初始阶段抗弯刚度Ki 的影响Fig. 11 Effects of different fine aggregate types on the initial section flexural stiffness of specimens
图12 比较了不同细骨料试件的使用阶段抗弯刚度系数F12,可见,对于剪跨比λ 为1.75 的圆形试件,原状海砂试件和淡化海砂试件的使用阶段抗弯刚度Ks与普通河砂试件相比增大,提高幅度分别为3.2%和4.8%;对于λ 为3.5 的圆形试件,原状海砂试件相对于普通河砂试件,Ks降低,降幅为15.9%,这主要是由于在剪跨比较大的情况下,构件受弯为主,此时海砂混凝土受拉区混凝土开裂较河砂混凝土更为严重,其裂缝分布区域更大,因此在使用阶段由于拉区混凝土退出工作引起的刚度下降幅度则相应的更为显著;混凝土淡化海砂试件相对于普通河砂试件,Ks升高,增幅为到14.4%;对于剪跨比λ 为1.75 的方形试件,原状海砂试件和淡化海砂试件的使用阶段抗弯刚度Ks与普通河砂试件相比均降低,降幅分别为5.0%和8.1%;对于λ 为3.5 方形截面试件而言,不同细骨料试件的Ks基本接近。总体而言,大剪弯比时,圆形试件中,原状海砂替代普通河砂对试件使用阶段刚度的影响较为显著,而在其他条件下,其影响较小。
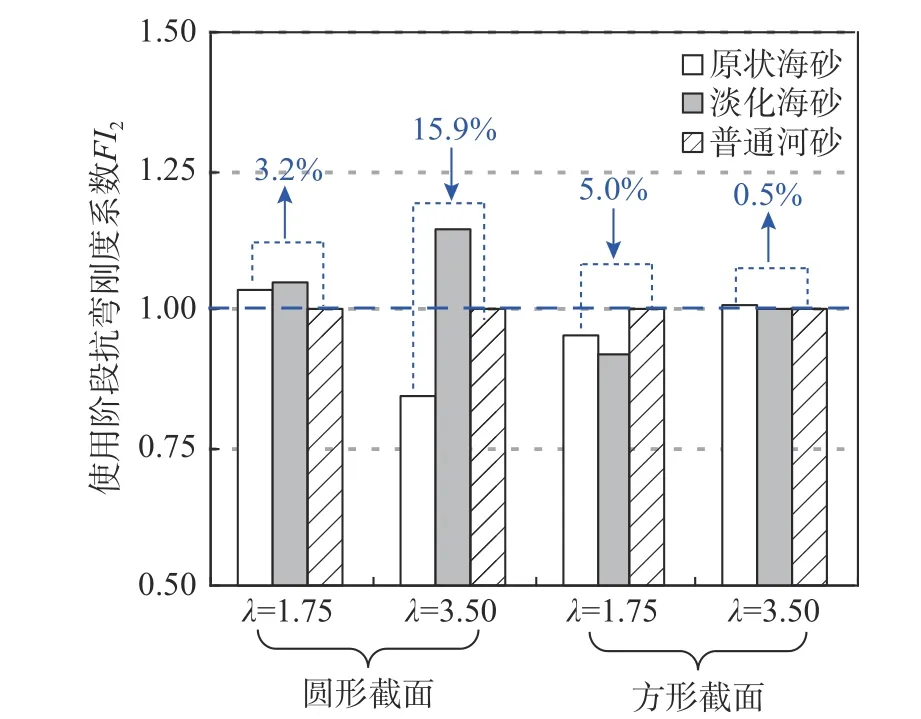
图12 不同细骨料对试件使用阶段抗弯刚度Ks 的影响Fig. 12 Effects of different fine aggregate types on the serviceability-level section flexural stiffness of specimens
为分析现行的钢管混凝土规范或规程对不锈钢管海砂(普通)混凝土抗弯刚度的适用性,选用了欧洲规范Eurocode4 (2004)[31]、美国钢结构协会规范ANSI/AISC 360-10 (2010)[32]、美国混凝土协会规范ACI 318-19 (2019)[33]和福建省地方标准《钢管混凝土结构技术规程》(DBJ/T 13-51-2010)[34]对本文试件抗弯刚度试验值和规范计算值进行了比较,表4 给出了选用的4 本规范抗弯刚度计算值和试验值比值的平均值和方差,可见EC4 规范计算的本文圆形试件初始抗弯刚度值和试验值比值的平均值μ为0.986,方差σ 为0.022,方形试件为0.992 和0.021,其所提供的抗弯刚度公式可满足于不锈钢管海砂(普通)混凝土的初始抗弯刚度的计算,如式(4)所示;ANSI/AISC 360-10 规范和ACI 318-19 规范计算的本文试件使用阶段抗弯刚度值和试验值的比值接近,其中利用ACI 318-19 规范所得的圆形试件使用阶段抗弯刚度计算值与试验值比值的平均值μ为1.052,方差σ 为0.135,方形试件为0.961 和0.074,可满足于不锈钢管海砂(普通)混凝土的使用阶段抗弯刚度的计算,抗弯刚度计算式如式(5)所示:
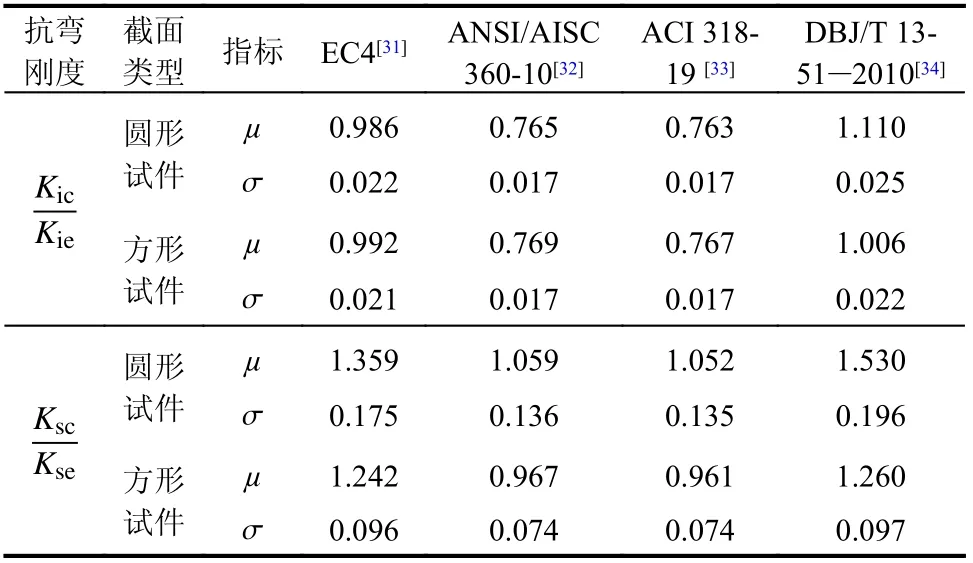
表4 抗弯刚度规范计算值与试验值比值的平均值和方差Table 4 Mean and standard deviation of the ratio between calculated and tested flexural rigidity values

3 有限元分析
3.1 有限元模型建立与验证
不锈钢采用Rasmussen[35]提出的应力σ-应变ε 模型,这主要是由于该不锈钢本构关系得到了Tao 等[36]的验证,精度高且要求输入参数少;不锈钢材真应力、真塑性应变与名义应力、名义应变之间的转换参考文献[36];对于方形截面,弯角区域范围、弯角区域不锈钢管屈服强度计算和初始缺陷模型参考文献[36]。此外,因核心混凝土的存在,不锈钢管焊接残余应力对不锈钢管混凝土构件力学性能的影响较小[36],其对构件整体性能影响可以忽略。
对于不锈钢管原状海砂混凝土、不锈钢管淡化海砂混凝土和不锈钢管普通河砂混凝土构件而言,三种核心混凝土均受到不锈钢管对其约束且该约束作用与其受到来自普通钢管的约束并无显著差异[13],且暂无考虑约束效应的海砂混凝土应力σ-应变ε 本构模型;此外,海砂混凝土的抗压强度、抗折强度等和同级别的普通河砂混凝土相差不大[6,8],且海砂取代率对海砂混凝土轴压力学性能的影响并不显著[37]。因此,核心混凝土均采用韩林海[38]提出的考虑约束效应的混凝土σ-ε 模型;混凝土受拉软化特性通过失效应力-断裂能模型来反映,文献[39]给出了开裂应力的计算公式。
图13 为所建立的不锈钢管混凝土纯弯构件有限元模型示意图,不锈钢管、端板和核心混凝土分别采用S4、C3D8R 单元模拟;考虑不锈钢管和核心混凝土之间的粘结滑移,其界面模型包括法向和切向两个方向,其中法向方向采用“硬接触模型”,切向方向采用“库仑摩擦模型”,不锈钢管和原状海混凝土、淡化海砂混凝土之间的界面摩擦系数参考不锈钢管与普通河砂的取值,均取0.25[13,36];端板和钢管混凝土之间的相对滑移可忽略,采用绑定约束Tie。在构件下部设立参考点RF1 和RF2,并将局部外钢管与二者耦合,约束点RF1 除绕X轴转动和沿Z轴平动自由度外其他4 个自由度,以模拟滚轴支座;约束点RF2 除绕X轴转动自由度外其他5 个自由度,以模拟固端铰支座;在试件上部四分点处设立参考点RF3 和RF4,将二者除沿Y轴平动自由度外其他5 个自由度全部进行约束并施加位移,进行加载。

图13 有限元模型示意Fig. 13 Schematic view of the finite element mode
图5 中给出了3 种 细骨料构件在弯曲荷载作用下的计算和试验实测弯矩M-跨中挠度um曲线,可见有限元计算结果和试验结果均吻合良好,表明采用的混凝土本构模型可适用于模拟不锈钢管约束海砂混凝土。同时,为进一步验证模型的准确性,计算了文献[16]、文献[21 - 22]、文献[40]和本文中共计40 根圆形和38 根方形不锈钢管混凝土构件的受弯承载力,计算值Muc1和实测值Mue比较见图14。可见,圆形构件的受弯承载力的计算值和实测值的比值Muc1/Mue的平均值u和方差σ 分别为1.037 和0.082;方形构件Muc1/Mue的u和σ 分别为1.012 和0.079。综上,所建立的不锈钢管混凝土纯弯构件有限元模型可用于重要参数对其力学性能的影响分析。

图14 受弯承载力有限元计算结果与试验结果对比Fig. 14 Comparisons of the test moment capacities with those calculated by finite element model
3.2 弯矩-应变曲线比较
利用上述有限元法分别建立了不锈钢管混凝土和普通钢管混凝土受弯构件有限元模型,其中普通钢的应力-应变关系采用文献[38]中二次塑流模型,普通钢管和核心混凝土之间的截面摩擦系数按文献[16]中建议,取0.6。图15 给出了与编号为C-SS-3.5 试件同规格(钢材屈服强度、核心混凝土强度、试件长度、钢管尺寸)的不锈钢管混凝土和普通钢管混凝土的弯矩M-跨中受拉区纵向应变εsl曲线比较,可见,相同约束效应下,不锈钢管混凝土的M-εsl曲线较普通钢管混凝土较早进入非线性阶段;不锈钢管混凝土构件受弯承载力εmax=10 000 με 大于普通钢管混凝土,在受荷后期,其受弯承载力能继续增大,而普通钢管混凝土受弯承载力在则相对不变,这与文献[16]的结论一致,主要是由于不锈钢较普通钢有显著应变强化特性。为不锈钢管混凝土的合理设计,需考虑不锈钢管与普通钢管的材料性能差异。
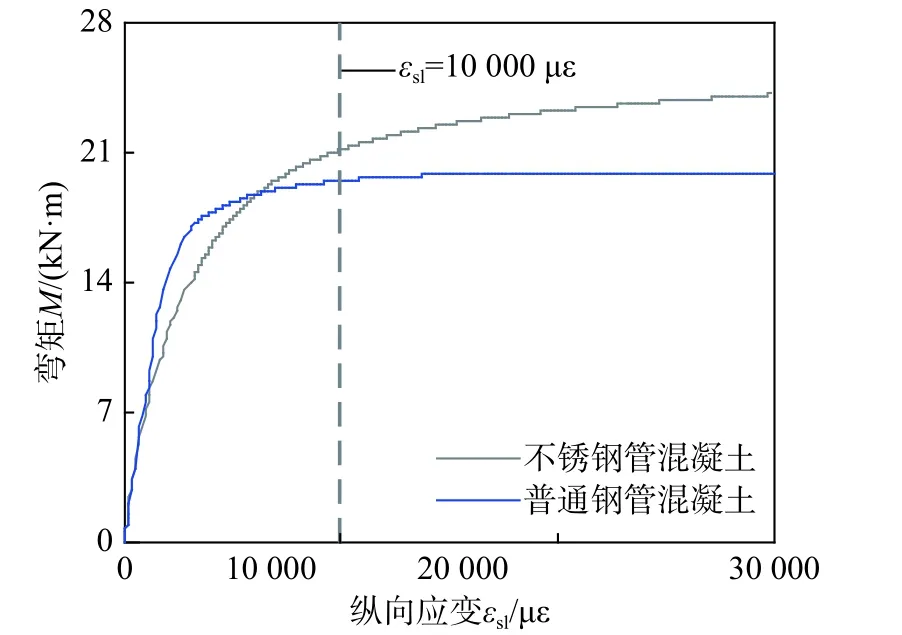
图15 圆形纯弯构件弯矩-纵向应变曲线比较Fig. 15 Comparisons of bending moment-longitudinal strain curves of concrete-filled circular steel tube
3.3 参数分析
利用所建立的有限元模型,分析了下列参数对受弯构件M/Wsc-εmax关系曲线的影响,其中Wsc为不锈钢管混凝土截面抗弯模量,εmax为截面纤维最大拉应变。变化的参数范围为:不锈钢屈服强度σ0.2为220 MPa、260 MPa、300 MPa、350 MPa、420 MPa 和480 MPa,核心混凝土强度fcu为40 MPa、60 MPa 和80 MPa,截面含钢率αs(αs=As/Ac,As为钢管横截面面积,Ac为核心混凝土横截面面积)为0.05、0.10、0.15 和0.20,其中不锈钢屈服强度根据文献[41]中所列的不同不锈钢类型选用。表现为构件的受弯承载力(εmax=10 000 με时)随着σ0.2、fcu和αs的增大而增大,即构件的受弯承载力与不锈钢管对核心混凝土的约束效应系数ξ(=(αs·σ0.2)/fck,其中fck为混凝土轴心抗压强度标准值)有关,图16 分别给出了核心混凝土强度为40 MPa、60 MPa 和80 MPa 时不同约束效应下的圆形和方形不锈钢管混凝土M/Wsc-εmax关系曲线,可见,同一核心混凝土强度下,无论圆心构件还是方形构件的受弯承载力均随着约束效应系数ξ 的增大而增大。值得注意的是,不锈钢管混凝土M/Wsc-εmax关系曲线与文献[38]中普通钢管混凝土M/Wsc-εmax关系曲线相比,曲线较早进入非线性阶段,这主要与不锈钢和普通钢材料性能差异有关。


图16 圆形不锈钢混凝土M/Wsc-εmax 关系曲线Fig. 16 M/Wsc-εmax curves of concrete-filled circular stainless steel tube
3.4 受弯承载力的简化计算
为和传统钢管混凝土抗弯承载力表达式一致,同时结合上述参数分析的结果,可知,不锈钢管混凝土构件的受弯承载力主要与构件截面的抗弯模量Wsc、约束效应系数ξ 及抗压强度指标fsc有关。其中,截面抗弯模量Wsc的计算参考文献[34],如式(6)和式(7)所示:
圆形截面:

方形截面:

圆形截面抗压强度fsc的计算参考文献[19],如式(8)所示:

方形截面抗压强度fsc的计算参考文献[42],如式(9)所示:

其中,fck为混凝土轴心抗压强度设计值。
在规范[34]建议的有关普通钢管混凝土构件受弯承载力的式(10)的基础上,采用有限元法,对适用于不锈钢管混凝土的有一定塑性发展的截面塑性弯矩与截面边缘刚达到屈服应力的时的截面屈服弯矩的比值即截面塑性发展系数γm(γm=Mu/(Wsc·fsc))与约束效应系数ξ 关系进行回归,如图17 所示,可见,在约束效应系数对等时,无论圆形截面还是方形截面,不锈钢管混凝土的截面塑性发展系数大于普通钢管混凝土,这主要与不锈钢较普通钢比例极限低,加载初期既表现出很强的非线性有关。圆形不锈钢管混凝土构件γm与ξ 的关系可表达为式(11),方形不锈钢管混凝土构件二者的关系可表达为式(12)。

图17 γm-ξ 关系Fig. 17 Flexural strength index γm-confinement factor ξ relations

圆形截面试件:
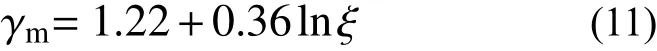
方形截面试件:

3.5 简化公式的准确性及适用范围
图18 为按简化公式对文献[16]、文献[21 - 22]、文献[40]和本文中共计40 根圆形、38 根方形不锈钢管混凝土构件计算得到的受弯承载力Muc2与试验结果Mue的对比情况,可见,圆形构件简化计算结果和试验计算结果的比值Muc2/Mue的平均值u与方差σ 分别为1.041 和0.113;方形构件Muc2/Mue的u和σ 分别为0.982 和0.107;上述对比结果表明对文献[34]建议的受弯承载力公式进行的修正,即可适用于不锈钢管普通河砂混凝土构件受弯承载力的计算亦可适用于不锈钢管海砂混凝土构件受弯承载力的计算。简化公式的适用范围为:不锈钢名义屈服强度σ0.2=220 MPa~480 MPa;混凝土立方体抗压强度fcu=40 MPa~80 MPa;截面含钢率αs=0.05~0.20。

图18 抗弯承载力简化计算结果与试验结果对比Fig. 18 Comparisons of the test moment capacities with those calculated by simplified model
4 结论
本文完成了24 根不同细骨料下不锈钢管混凝土在纯弯荷载作用下的力学性能试验,并利用所建立的有限元模型提出了不锈钢管混凝土受弯承载力计算的简化公式,在所探讨的参数范围内可得到以下结论:
(1)无论是圆形试件还是方形试件,其整体的破坏模态并没有因细骨料种类的不同而有显著区别;但原状海砂混凝土受拉区裂缝数量较河砂混凝土多且部分裂缝贯穿至中性轴以上,三种细骨料试件的荷载-变形曲线均未出现下降段,表现出良好的延性。
(2)原状海砂和淡化海砂对不锈钢管混凝土构件的受弯承载力和初始阶段抗弯刚度影响较小,大剪跨比时,圆形试件中原状海砂替代普通河砂对试件的使用阶段抗弯刚度影响显著,而在其他条件下此影响较小,表明海砂可替代普通河砂形成不锈钢管海砂混凝土构件,且其力学性能良好。
(3)剪跨比对于原状海砂的圆形试件的受弯承载力影响相对于其他两种细骨料圆形试件较大:剪跨比为3.5 的原状海砂圆形试件的受弯承载力较剪跨比为1.75 的原状海砂圆形试的受弯承载力降低12%,同等情况下的普通河砂圆形试件降幅为2.2%;剪跨比对各试件初始阶段的抗弯刚度的影响较小;对各试件的使用阶段的抗弯刚度影响明显:剪跨比小的试件较剪跨比大的试件使用阶段抗弯刚度均有不同程度提高,圆形试件增幅为5.2%~29.0%;方形试件增幅为9.7%~13.1%。
(4)建立了圆形、方形不锈钢管混凝土有限元分析模型,在验证模型可靠性的基础上,开展参数分析,在福建省地方标准DBJ/T 13-51-2010 的基础上,基于参数分析的结果,回归了适用于不锈钢管混凝土构件受弯承载力的计算公式,为有关工程实践提供参考。

