基于天牛群算法的虚拟同步发电机最优控制策略研究

王枫淇，叶 鹏，刘思奇，杨 硕，屈科明

（沈阳工程学院 电力学院，辽宁 沈阳 110136）

传统电力系统通过同步发电机的转子储存大量能量，用于抑制负荷波动及调节频率，但新能源并网所需的并网逆变器不存在转子储能［1-2］。

通过虚拟同步发电机（VSG）控制并网逆变器，实现传统同步发电机调压调频的功能已成为国内外学者研究的重点［3-5］。

本文从并网逆变器的频率和电压角度出发，对VSG 中虚拟惯量和阻尼进行了分析，并得到参数的约束范围。以多个系统优化为目标函数，采用改进的多目标天牛群最优控制算法求取虚拟惯量和阻尼的最优值。

1 虚拟同步发电机模型

并网逆变器拓扑结构如图1 所示。Rf、Cf、Lf分别为RLC电阻、电容和电感，iL、UC分别为电感电流和电容电压，Ug为电网电压，e为内部电势，Lg为电网电感，Udc、Cdc分别为直流端电压和电容，S1～S6为逆变器的控制开关。

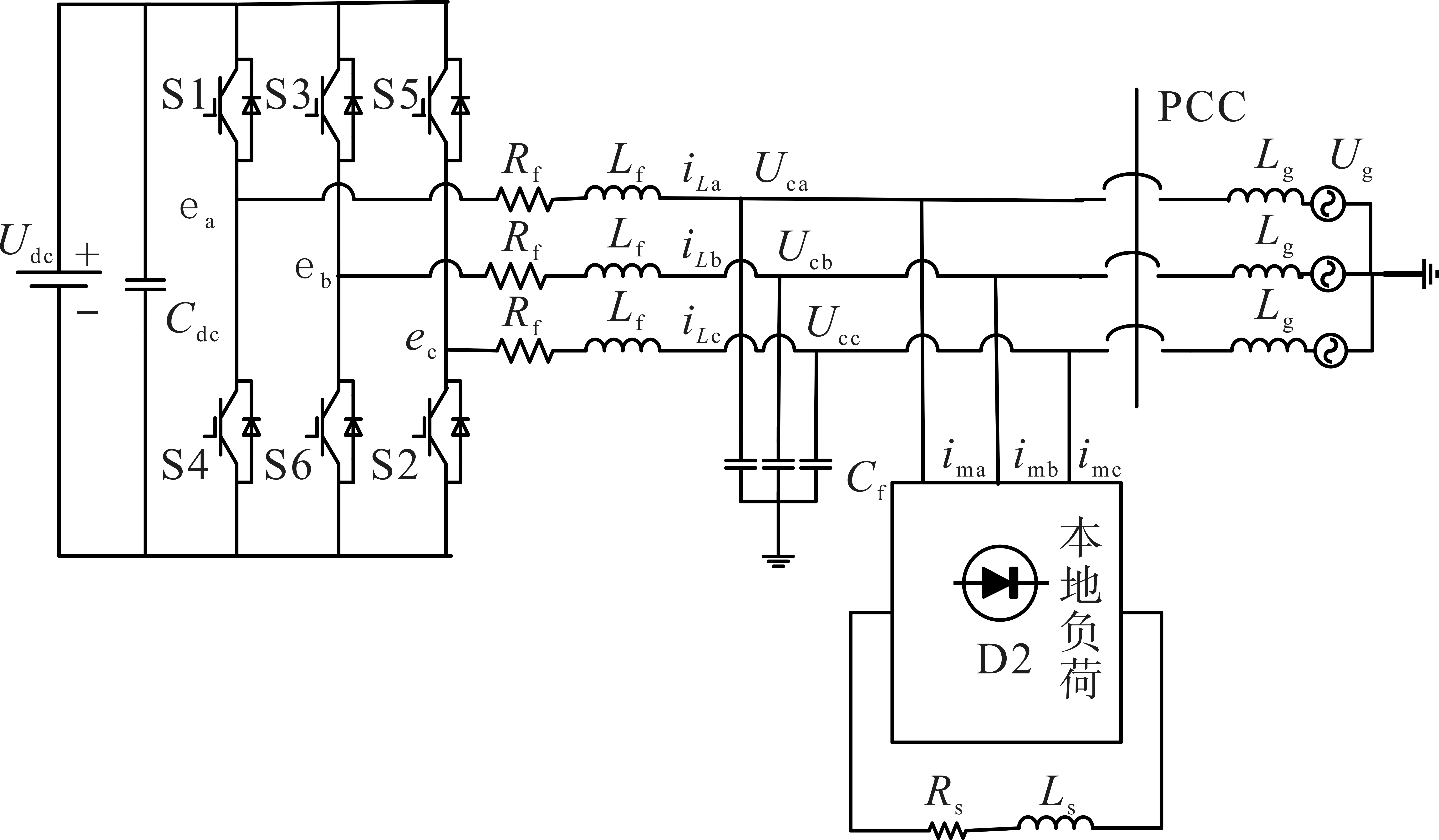
图1 并网逆变器框图

虚拟同步发电机控制电路如图2 所示。f、fn分别为电网频率及参考频率，Qref、Q分别为无功功率参考值和无功功率，J为虚拟惯性时间常数，ωn为参考角频率，Pm、Pe分别为新能源的机械功率和输出功率，D 为阻尼系数，δ为相位角，Kp、Kq分别为有功频率下垂系数和无功电压下垂系数，Mabc为调制信号。

首先，在VSG 控制算法中引入有功-频率和无功-电压下垂特性，再通过同步机的转子方程获取相位角，电压有效值与相位角合成参考电压值，并送入虚拟阻抗控制模块中产生底层电压电流参考信号。底层电压电流输出控制信号到空间矢量脉宽调制（SVPWM）获得脉冲调制信号，以此来控制桥臂的通断。

VSG 控制算法的核心是在控制方程中引入虚拟惯量和阻尼，从而为电网提供惯量和阻尼支撑。转动惯量公式如下：

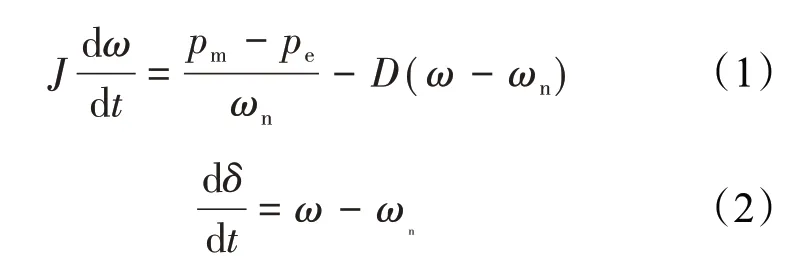
由上述系统分析可知，VSG 有功开环和闭环传递函数为［6］

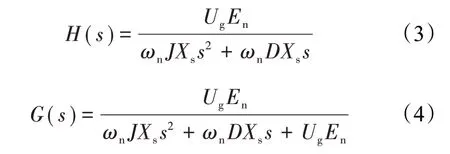
2 转动惯量和阻尼分析

2.1 频率稳定分析

由图1可知：

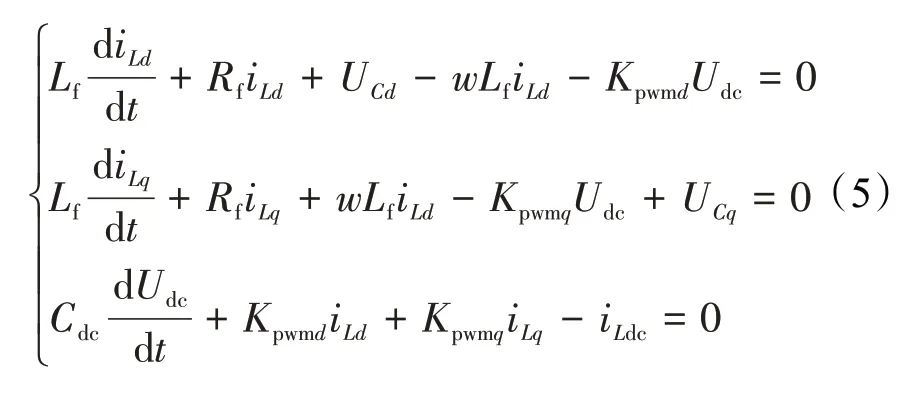
式中，iLd、iLq、UCd、UCq分别为dq旋转坐标轴下的电感电流和电容电压。

式（5）经过整理后可以得到如下等式：

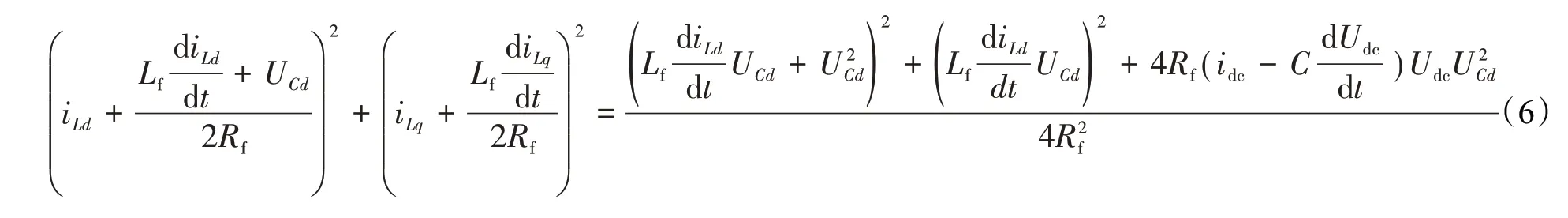
以旋转坐标系d轴为电压合成方向，有功功率与无功功率表达式如下：

将式（6）、（7）合并可以写成：

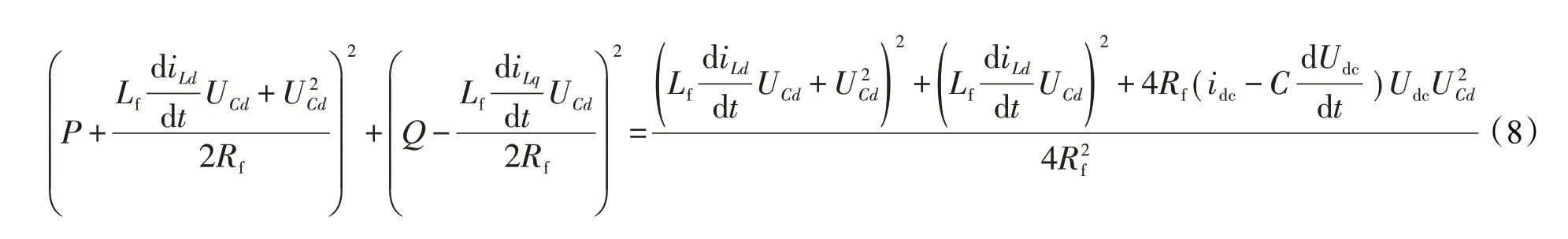
无功下垂特性等式：

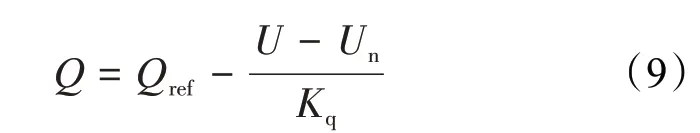
因此，逆变器电压与角频率的关系如下所示：

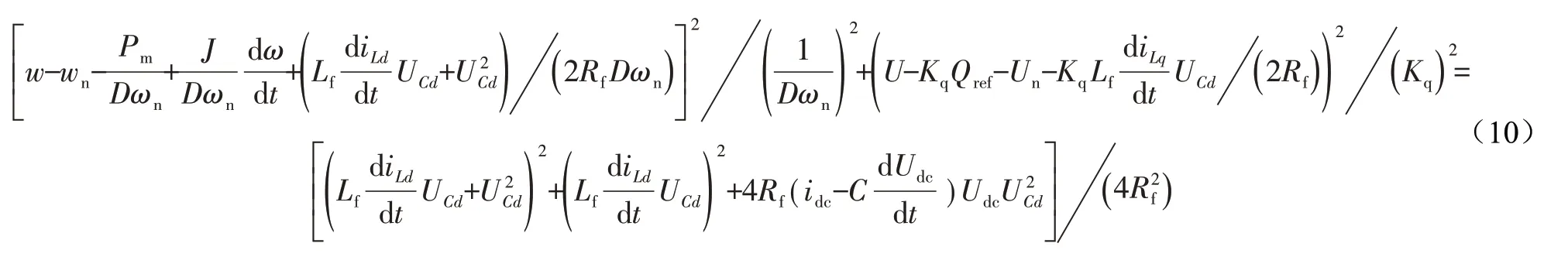
2.2 虚拟惯量和阻尼约束

通过VSG 的开环等式（3）可得系统的截止频率为

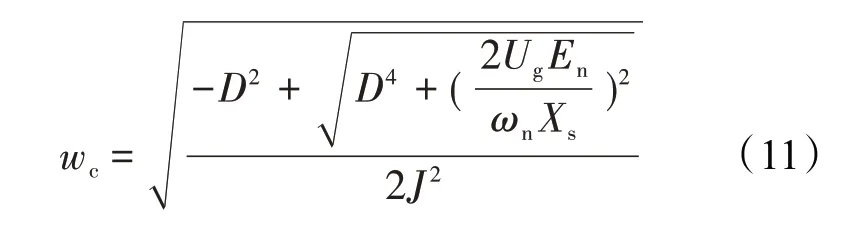
式（11）的曲线如图3 所示。虚拟惯量和阻尼的引入对系统的角频率产生较大的影响，对电压的取值范围不存在影响，即虚拟惯量和阻尼的不同取值会改变系统的状态点并影响角频率的取值范围。

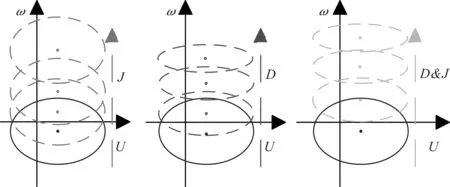
图3 ω-U曲线

由VSG 的闭环等式（4）可知，系统是一个典型二阶系统，通常二阶系统的截止频率处的斜率为-20 dB/dec 时，具有较好的稳定裕度。因此，系统的转折频率要高于截止频率，为降低功率的脉动量，转折频率应小于1/10 的电网频率，可得到如下等式：

为满足系统的暂态要求，系统工作在欠阻尼下，阻尼取值范围为0.4～0.8，虚拟惯量和阻尼的取值范围如下：

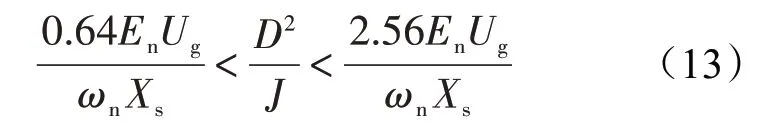
3 多性能目标函数

当系统负荷发生波动时，系统频率发生振荡，如图4 所示，tst为调节时间。为提高系统的整体性能，系统的多性能目标函数表达如下：

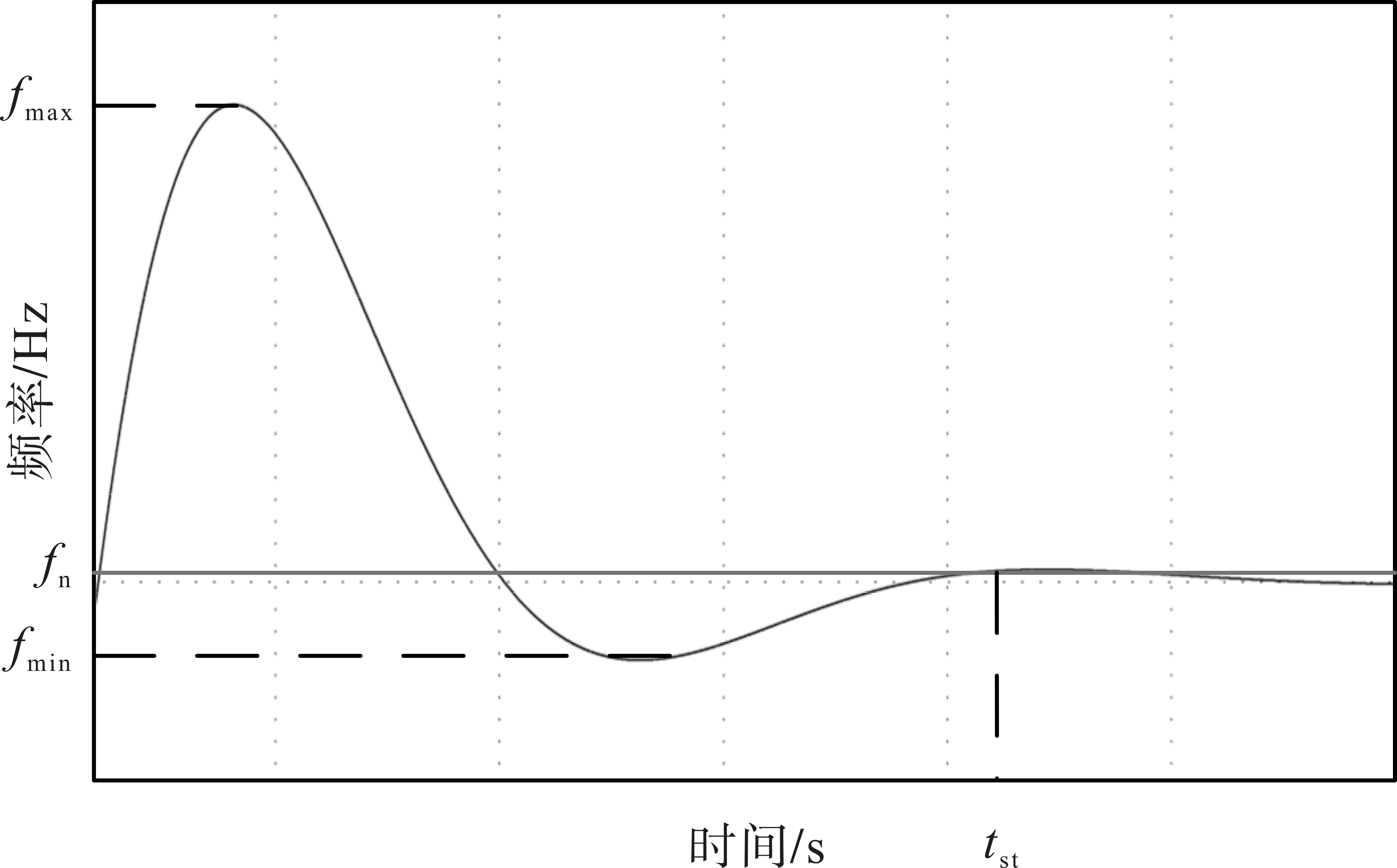
图4 频率波动

①频率偏差：频率偏差超出一定范围后会触发系统的保护动作，系统变成应急响应状态，这是所不期望的，因此选取频率最大差值如下：

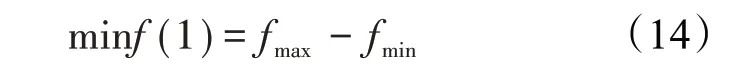
②调节时间：系统的持续振荡会带来不稳定因素，也会影响系统的控制精度：

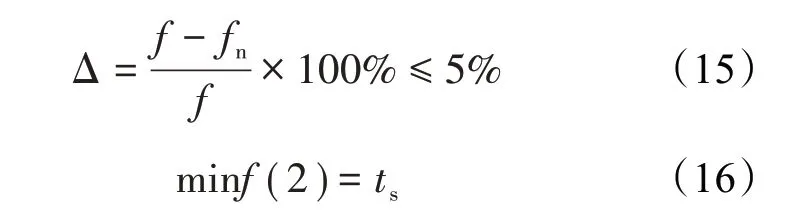
③储能优化：由式（1）可知虚拟惯量和阻尼对应的功率为

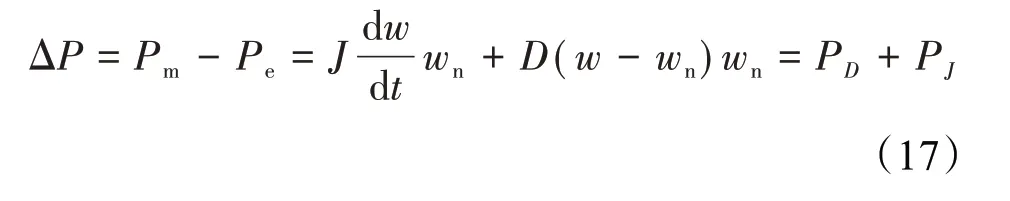
由式（17）可知，系统的储能容量跟虚拟惯量和阻尼相关，因此为降低系统对储能上限的需求，以式（18）作为储能单元的优化。

④时间乘绝对误差积分函数（ITAE）：ITAE 指标能体现系统响应的超调量和快速性，因此本文采用ITAE作为目标函数来消除稳态误差。

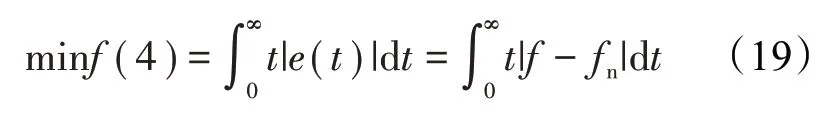
4 多目标天牛群优化算法

4.1 基本天牛群优化算法

由于粒子群（PSO）优化算法具有较少的参数调节，并且在实际工程应用中更易实现，所以粒子群优化算法应用于VSG 控制参数寻优中具有较高的实际效益。但是粒子群算法［7］也有其缺陷，因此通过对粒子群进行改进获取天牛群优化算法。

天牛群优化算法（BSO）是通过天牛须算法（BAO）［8］优化粒子群算法中的粒子寻优过程进行改进的。PSO 最大的缺陷在于粒子本身缺乏对环境的判断，通过引入BAO 中天牛须对环境判断的依据而优化PSO 中的粒子，使其不易陷入局部最优，并且获得较快的收敛速度。

BSO 数学公式如下：

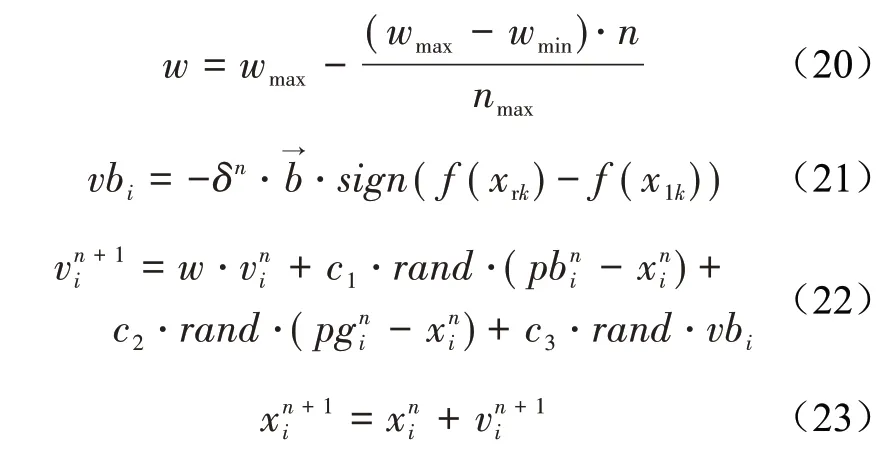
4.2 多目标天牛群优化算法

不同目标函数之间是存在冲突的，因此多目标函数问题就无法像单目标函数一样直接通过BSO算法进行求解。传统多目标粒子群优化算法［9］有多种不同的实现方式，有学者将不同的目标函数以不同的权重进行结合形成一个目标函数，即线性加权，或者将一个目标作为优化目标，其他目标作为惩罚函数存在，即e-约束。这两种方式都是通过对目标函数进行缩放和归一化为一个目标函数实现的，在这个过程中会丢失大量的优化解，优化不是很理想。因此，本文选取帕累托方法实现多目标函数的构建。使用帕累托方法可以将多目标天牛群优化算法寻找出的解空间进一步缩小为帕累托解空间，获取更多的有效解。

帕累托前沿示意图如图5 所示，在一群可行解中选取一些优化解作为帕累托前沿，并在帕累托解中选择一组较满意的解。基于帕累托实现多目标天牛群优化算法（PMOBSO）的重点在于判断天牛个体环境，选取个体历史最优解及全局最优解。

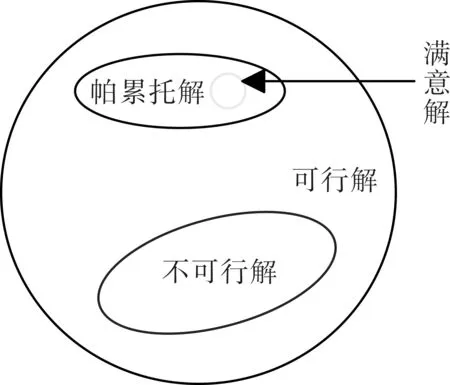
图5 帕累托前沿

天牛个体在多个目标下对环境的判断会存在冲突，如本文中4 个目标函数会导致天牛个体进行4 次的环境判断，可能有3 个目标函数环境的判断相同，为实现优化目标的最大化，采取多数目标倾向大于少数目标倾向的方法，目标倾向相同时，随机选取。

全局最优解的选取是根据拥挤程度选择一个领导者，在应用自适应网格法对最优解集和领导者进行更新，具体公式已有大量文献说明。

4.3 PMOBSO算法步骤

PMOBSO算法步骤如下：

1）初始化天牛群参数，确定学习因子可以固定化选取，以保证后续的参数分析。

2）天牛个体通过式（21）对环境进行判断，获得个体前进方向。

3）按式（22）和（23）更新位置和速度，判断位置是否超过虚拟惯量和阻尼的取值边界，如果超过选取临界的边界值。

4）更新个体及群体的最优位置及最佳适应度值，获得帕累托前沿。

5）判断适应度和迭代次数是否达到要求，如果不满足，则回到步骤2）进行下一次迭代；如果满足需求，则输出计算结果。

5 仿真实验

本文在Matlab/Simulink 仿真环境下搭建了图1所示的VSG 并网逆变器，验证所提出的BSO，系统主要参数如表1所示。

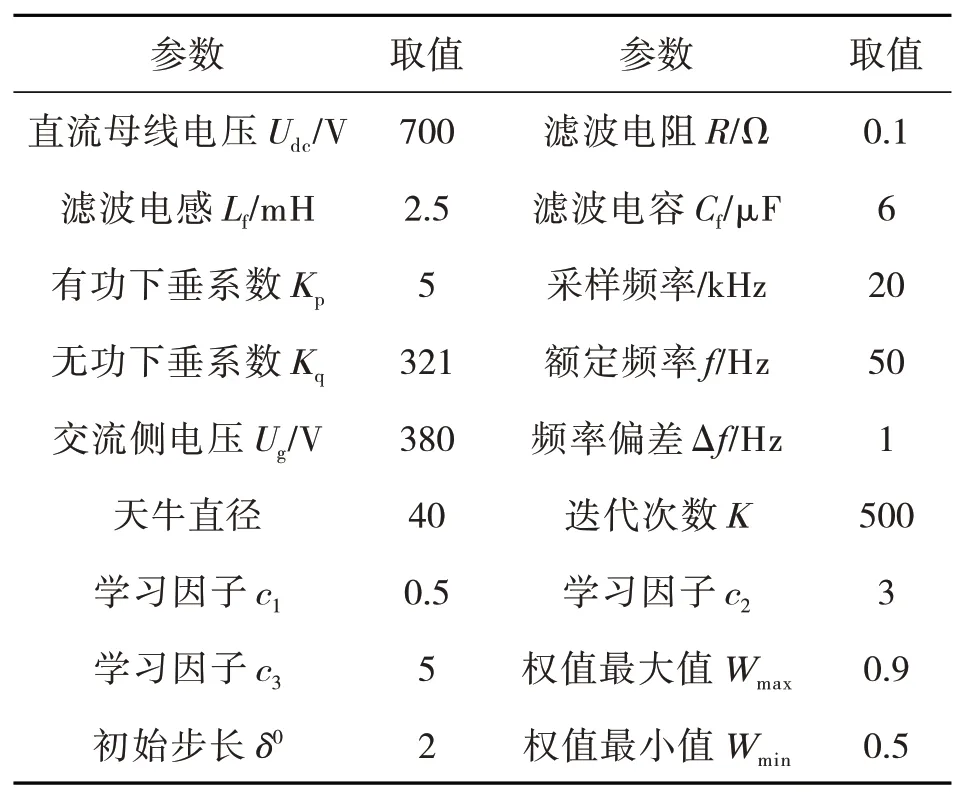
表1 并网逆变器及BSO 算法的主要系统参数

5.1 VSG功能验证

系统初始以Pe=10 kW 有功功率稳定输出。当t=2.5 s 时，负荷功率由10 kW 增至11 kW，系统输出电流和输出功率如图6 所示，并网逆变器在经历一定振荡后稳定输出功率。

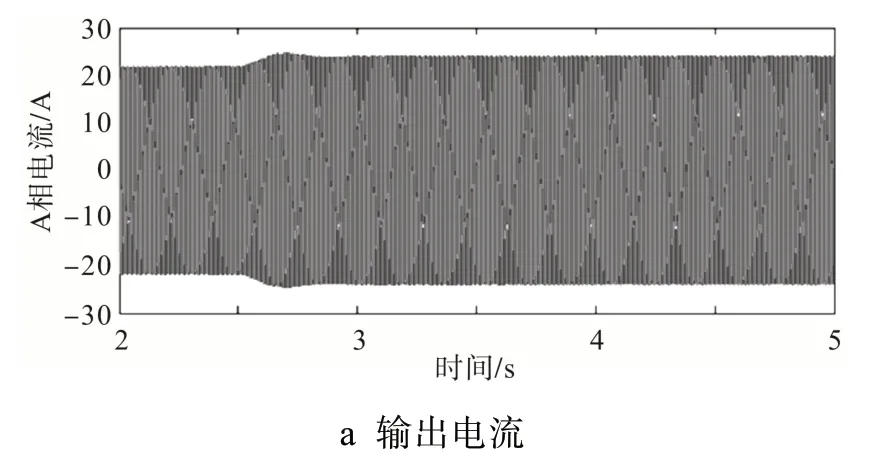
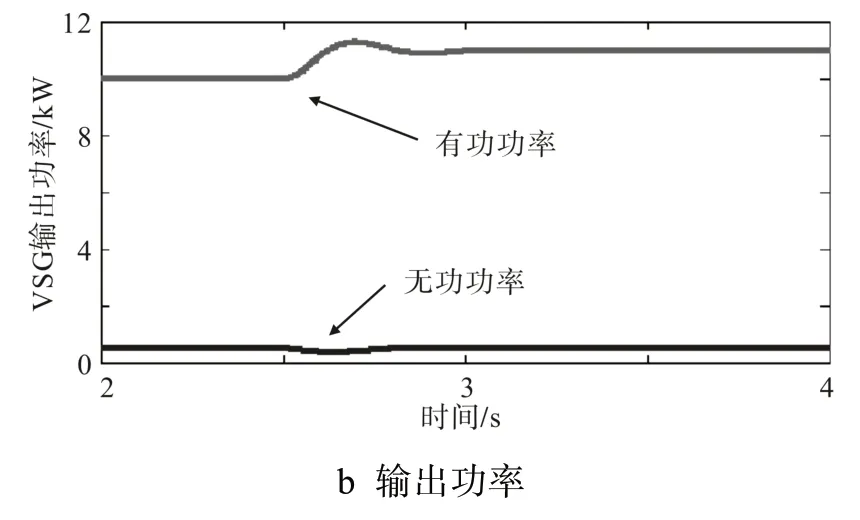
图6 负荷功率变化

图7 为选取的一组帕累托前沿，由图可知不同目标函数间存在冲突，无法直接获得一组理想的最优解，在帕累托前沿中选取一组解即可视为最优解。本文依据实际情况，以稳定为优先优化目标，选取频率偏差为第一要素，从而筛选帕累托前沿中的解。

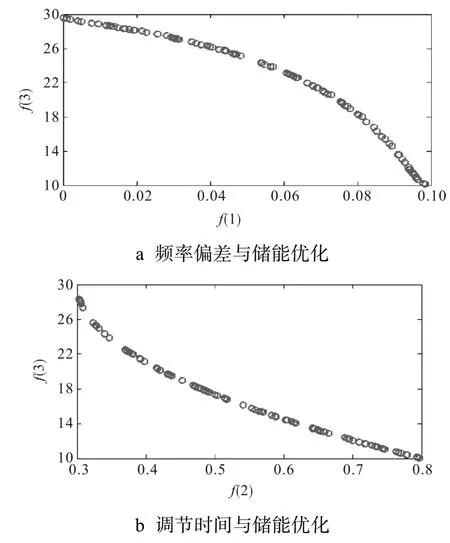
图7 Pareto非劣解集

5.2 负荷功率变化

根据我国入网频率的要求，分别考虑负荷变化1 kW 和8 kW 时，系统频率的变化情况，PMOB‐SO1 系统取值J=2.5，D=15；PMOBSO2 系统取值J=2.5，D=25。为了具有对比性，仿真对比图中加入无VSG控制的并网逆变器（OVSG）。

1）情况一：负荷功率变化1 kW。

初始状态下，系统以10 kW 有功功率稳定运行。当t=2 s 时，负荷功率由10 kW 增加至11 kW，系统变化情况如图8 所示。由图8 可以看出，OVSG 的频率最大值超出电网入网频率要求，PMOBSO1和PMOBSO2虽然参数不同，但都稳定运行在入网频率要求范围内，其中PMOBSO2 相比于PMOBSO1 的频率偏差更小，但PMOBSO1的储能优化更好，并且调节时间更短。

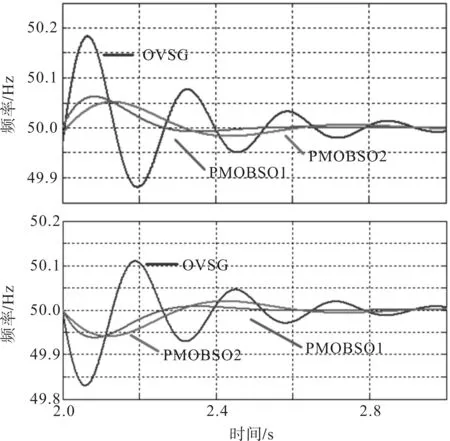
图8 负荷变化1 kW频率波动

2）情况二：负荷功率变化8 kW。

初始状态下，系统以10 kW 有功功率稳定运行。当t=2 s 时，负荷功率由10 kW 增加至18 kW，系统变化情况如图9 所示。由图9 可以看出，OVSG 的频率最大值超出电网入网频率要求。与图9 变化相比，在应对较大的负荷功率变化时，系统的频率偏差和调节时间变得更差。

5.3 虚拟惯量和阻尼影响

为探讨VSG 中虚拟惯量和阻尼对系统频率的影响情况，通过常惯量VSG1（CVSG1）、VSG2（CVSG2）及PMOBSO 对系统频率的变化情况进行分析，表2为不同虚拟惯量和阻尼取值。

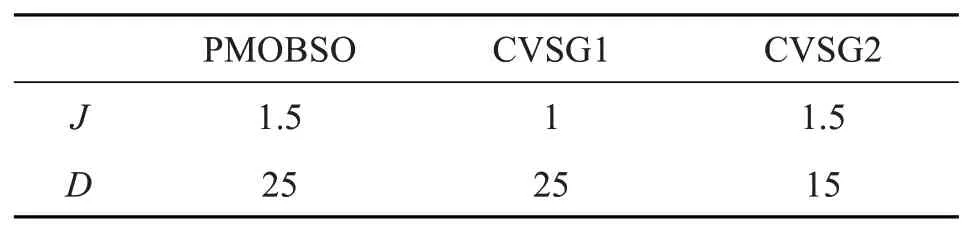
表2 不同虚拟惯量和阻尼取值

初始状态下，系统以10 kW 有功功率稳定运行。当t=2 s 时，负荷功率由10 kW 增加至11 kW，系统变化情况如图10 所示。由PMOBSO 和CVSG1对比可知，虚拟惯量取值越小，系统的频率振荡越小，但系统的频差更大；由PMOBSO 和CVSG2 对比可知，虚拟阻尼取值减小会提高系统的频差，并且增加调节时间，但会大幅度减少储能功率临界要求。

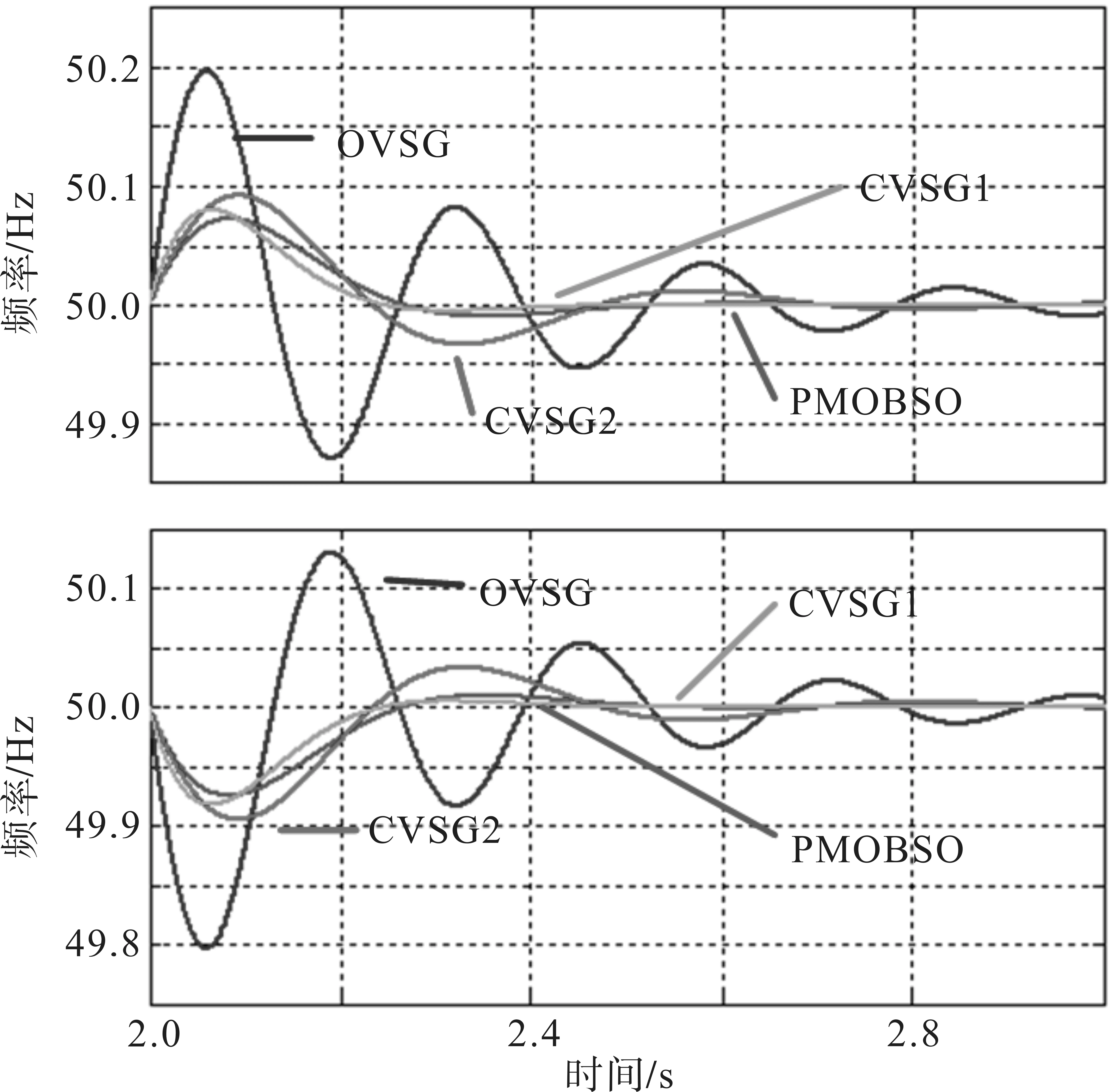
图10 负载变化1 kW频率波动

6 结论

如何在衡量系统稳定性与储能物理约束下定量表征虚拟惯量和阻尼的取值，本文在综合考虑系统的暂态特性和稳定特性下，确定虚拟惯量和阻尼的约束范围。为实现系统整体性能的提升，本文通过天牛群优化算法对多个性能指标进行了优化，通过帕累托获得一组最优解，仿真结果表明：

1）所提算法可以保证系统稳定运行于负荷波动较大的状态下，同时减少对储能物理上限的要求，优化储能单元。

2）初步探讨了虚拟同步发电机中虚拟惯量和虚拟阻尼的作用。虚拟惯量会降低频差，但会增加调节时间；虚拟阻尼会抑制系统的频差，降低调节时间，但储能物理的上限要求更高。

本文所提算法为实现系统的整体性能提升提供了一个解决方案，可以有效降低负荷变化对电网造成的影响。