基于钻柱屈曲的大位移井套管磨损预测模型

顾 岳, 高德利, 杨 进, 黄文君, 聂帅帅

(1.中国石油大学(北京) 石油工程教育部重点实验室,北京 102249; 2.承德石油高等专科学校石油工程系,河北承德 067000)

大位移井由于井深长,狗腿度严重,钻柱摩阻扭矩大等原因,套管的磨损问题十分严重[1-5]。目前现场实测的大位移井套管磨损深度普遍比通用模型计算出的磨损深度大,甚至很多大位移井出现了套管磨穿的现象。许多学者建立了大位移井套管磨损预测模型[1-3,6-8]。这些模型相较于传统的套管磨损模型,考虑了钻柱的刚度以及由于钻柱屈曲所导致的附加载荷等因素。在大位移井的钻井过程中,钻柱容易发生屈曲变形[9-17],前人的大位移井套管磨损预测模型只考虑了钻柱屈曲所引起的附加载荷[1-3]以及套管截面几何变化[6-8],而忽略了钻柱进尺长度的变化。对于普通井,由于井段的长度较小,钻柱发生屈曲的可能性较小,发生屈曲后的钻柱进尺长度变化量也不大;而大位移井由于井深较大,狗腿度严重,钻柱更容易发生屈曲,屈曲段的钻柱进尺长度变化量往往很大,如果在套管磨损的计算中忽略了屈曲段的钻柱进尺长度变化,会极大地影响套管磨损预测的精度。但是关于钻柱屈曲导致的钻柱进尺长度变化量对套管磨损影响的研究尚未见报导。笔者考虑由钻柱屈曲所导致的钻柱进尺长度变化量建立针对大位移井的套管磨损预测模型,结合采用“井工厂作业”模式下的南海流花某大位移井W1的井径测试数据,对邻井W2进行套管磨损预测,并和不同套管磨损预测模型的预测结果进行对比分析。

1 模型假设

(1)在大位移井钻井作业过程中,由于井深大,狗腿度严重,特别当钻柱发生屈曲时,钻柱本体会与套管接触,这极大地加剧了套管的磨损。所建立的模型中,认为在大位移井钻井作业过程中,钻柱本体与套管接触,忽略钻柱接头的影响[6-8]。

(2)所建立的套管磨损预测模型中考虑钻柱的正弦屈曲和螺旋屈曲效应。

(3)井筒内壁处于清洁状态。

(4)受大位移井增斜段井眼轨迹的影响,处于增斜段的钻柱稳定性提高,屈曲临界载荷很大[25],增斜段的钻柱不会发生屈曲。

(5)不考虑钻柱的涡动。

2 套管磨损预测几何模型

图1为大位移井钻柱下入的示意图。由图1可以看出:在钻柱下入大位移井的过程中,当钻柱的轴向力超过某个临界值时,钻柱就会发生屈曲,钻柱轴线不再与井眼轨迹轴线保持平行[9-17];在相同长度的井段中,屈曲后的钻柱进尺长度比没有发生屈曲的钻柱进尺长度要大,这会影响到套管磨损深度的计算。

套管磨损预测的几何模型可以根据计算点的钻柱所处的屈曲状态进行分类,本文中将钻柱的屈曲状态分为无屈曲、正弦屈曲和螺旋屈曲3类,如图2所示。

图1 大位移井钻柱形态示意图Fig.1 Sketch map of state of drill string for extended reach well

如图2(a)所示,对于未发生屈曲的钻柱,在计算点沿与钻柱轴线垂直的截面切开,该位置的套管磨损面积[18]的计算公式为

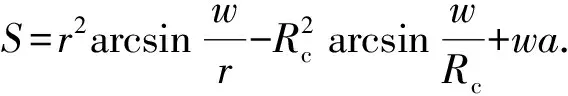
(1)

式中,r为钻柱的半径,m;Rc为套管的半径,m;w为套管的磨损槽半宽,m;a为钻柱与套管的轴线偏心距,m。

根据几何关系,钻柱与套管的磨损深度d可以表示为

d=a+r-Rc.

(2)

磨损槽半宽与偏心距的关系为

(3)

如图2(b)所示,对于在计算点发生正弦屈曲的钻柱,在计算点沿与钻柱轴线垂直的截面切开,套管截面为空心椭圆,在该位置处的套管磨损面积[6]的计算公式为

(4)

式中,ψN为屈曲后的钻柱与套管轴线的空间夹角,(°)。

如图2(c)所示,对于在计算点发生螺旋屈曲的钻柱,计算点沿与钻柱轴线垂直的截面切开,套管截面为空心椭圆,在该位置处的套管磨损面积[8]计算公式为

β(m2-m1).

(5)

式中,t为空心椭圆套管的厚度,m;p和q分别为空心椭圆套管内壁的椭圆几何方程的长轴半径和短轴半径,m;α为空心椭圆套管内壁的偏心距,m;β为钻柱圆形截面的偏心距,m;m1和m2为空心椭圆套管内壁与钻柱圆形截面交点的横坐标,m。

3 大位移井套管磨损深度预测模型

套管磨损的预测方程也可以通过能量法[18]推导,该方法认为钻柱的旋转是导致套管磨损的主要原因,在井下某位置处的套管磨损面积[1-3,6-8]计算公式为

(6)

式中,S为井下某一位置处的套管磨损面积,m2;μ为摩擦系数;n为转盘转速,r/min;N为钻柱与套管之间的接触力,N;fw为磨损影响因子,m/N;D为钻柱外径,m;Lm为钻柱进尺长度,m;vrop为钻速,m/h;L为计算点处钻柱和套管之间的相对滑动距离,m。

式(6)中Lm的取值为计算点到钻头的井段长度[1-3,6-8],即默认为钻柱轴线与井筒轴线平行,然而当钻柱发生屈曲时,钻柱轴线不再与井筒轴线平行,同一井段内钻柱的长度要大于井段的长度,Lm的取值必然比计算点到钻头的井段长,因此需要对钻柱屈曲后的Lm进行计算。假设通过计算点的管柱包含未发生屈曲的钻柱段、发生正弦屈曲的钻柱段、发生螺旋屈曲的钻柱段,如图3所示。

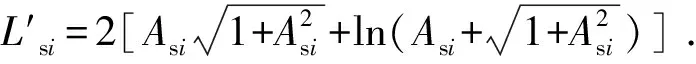
(7)

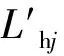
(8)

式(6)可以改进为

(9)

式中,nk、Dk、Nk和vropk分别为未发生屈曲的第k段钻柱的转盘钻速、管柱外径、接触力和钻速;ni、Di、Ni和vropi分别为螺距为Δhj的正弦屈曲钻柱段的转盘钻速、管柱外径、接触力和钻速;nj、Dj、Nj和vropj分别为螺距为Δhj的正弦屈曲钻柱段的转盘钻速、管柱外径、接触力和钻速。

式(9)和(6)的差别在于式(6)中的钻柱进尺长度Lm并未考虑钻柱屈曲所带来的影响,即式(6)中的Lm项即为式(9)中Lk的求和项。如果钻柱发生屈曲,则式(6)中的Lm项即为式(9)中未屈曲段Lk的求和项、正弦屈曲段Li的求和项、螺旋屈曲段Lj的求和项这3项之和。

可以根据文献[19]中的整体管柱力学模型计算出井下钻柱各个计算点的轴向载荷,通过比较计算点的轴向载荷与正弦屈曲临界载荷[20]和螺旋屈曲临界载荷[21]之间的关系,可以判断该位置处的钻柱是否屈曲,处于何种状态的屈曲。Gao等[22]推导出了正弦屈曲钻柱螺距、正弦幅度Ai等参数与钻柱轴向载荷的关系;Lubinski等[23]推导出了螺旋屈曲钻柱的螺距等参数与钻柱轴向载荷的关系。

将上述文献模型所计算出的参数与钻进参数代入由能量法推导出的套管截面磨损面积公式(9)中,可得到计算点的套管磨损面积S,然后根据计算点钻柱的屈曲形态,选择对应的由几何法推导出的套管截面磨损面积公式(1)～(3)中的一个,进行迭代计算,最终可以计算出该计算点的套管磨损深度。

建立的大位移井套管磨损预测模型的计算流程如图4所示。

图4 大位移井套管磨损预测模型的计算流程Fig.4 Calculation flowchart for casing wear prediction of extended reach wells

4 实例分析

算例数据来自中国南海LH11-1油气田的大位移井W1。南海深水油气资源丰富,但作业条件恶劣,在作业过程中需要预防钻井事故发生,因此精确预测套管磨损十分重要。

4.1 磨损影响因子反演对比

在基于能量法的套管磨损预测计算中,磨损影响因子fw的取值至关重要,不同井深位置处的磨损影响因子fw一般通过反演的方法得到:获取与目标井井身结构相似的邻井井径测试数据,将其代入到套管磨损预测模型中进行反演计算,得到相应的fw。该值可以被用于具有相同井身结构和井眼轨道设计的目标井套管磨损预测计算中。

W1井是已钻井,W2井是目标井。W1井和W2井的井身结构设计如表1和图5所示。

表1 W1与W2的井身结构关键点

图5 W1与W2井井身结构对比Fig.5 Comparison of casing program between well W1 and W2

由表1和图5可知,W1井和W2井井身结构设计、井眼轨道设计相似,因此W1井反演出的磨损影响因子可以用于W2井的套管磨损预测。

轴向摩阻系数设为0.1,周向摩阻系数设为0.25,该井三开的钻进参数为钻压90 kN、平均机械钻速4.17 m/h、转速120 r/min。由管柱力学模型[19]计算结果可知,W1井425～850、2 100～2 600 m井深处的钻柱处于正弦屈曲状态,2 600～2 750 m井深处的钻柱处于螺旋屈曲状态,其余井深位置处的钻柱未屈曲。

通过井径测试,得到了W1井各测深处的套管磨损深度(图6中的红线),将其分别带入Sun等[17]模型(钻柱未屈曲)、谭雷川等[6,8]模型(不考虑钻柱进尺长度变化)以及本文中建立的考虑钻柱屈曲导致的钻柱进尺长度变化量的套管磨损预测模型中进行反演计算。不同模型反演出的磨损影响因子如图6所示。

若不考虑钻柱屈曲引发的附加载荷、套管截面几何变形和钻柱进尺长度变化量(图6蓝线),如果钻柱发生屈曲,屈曲段和屈曲段前的井段反演出的套管磨损影响因子fw较小,用其预测目标井相应井深处的套管磨损情况,会使目标井相应井段的套管磨损预测值偏小,套管磨损严重程度被低估。

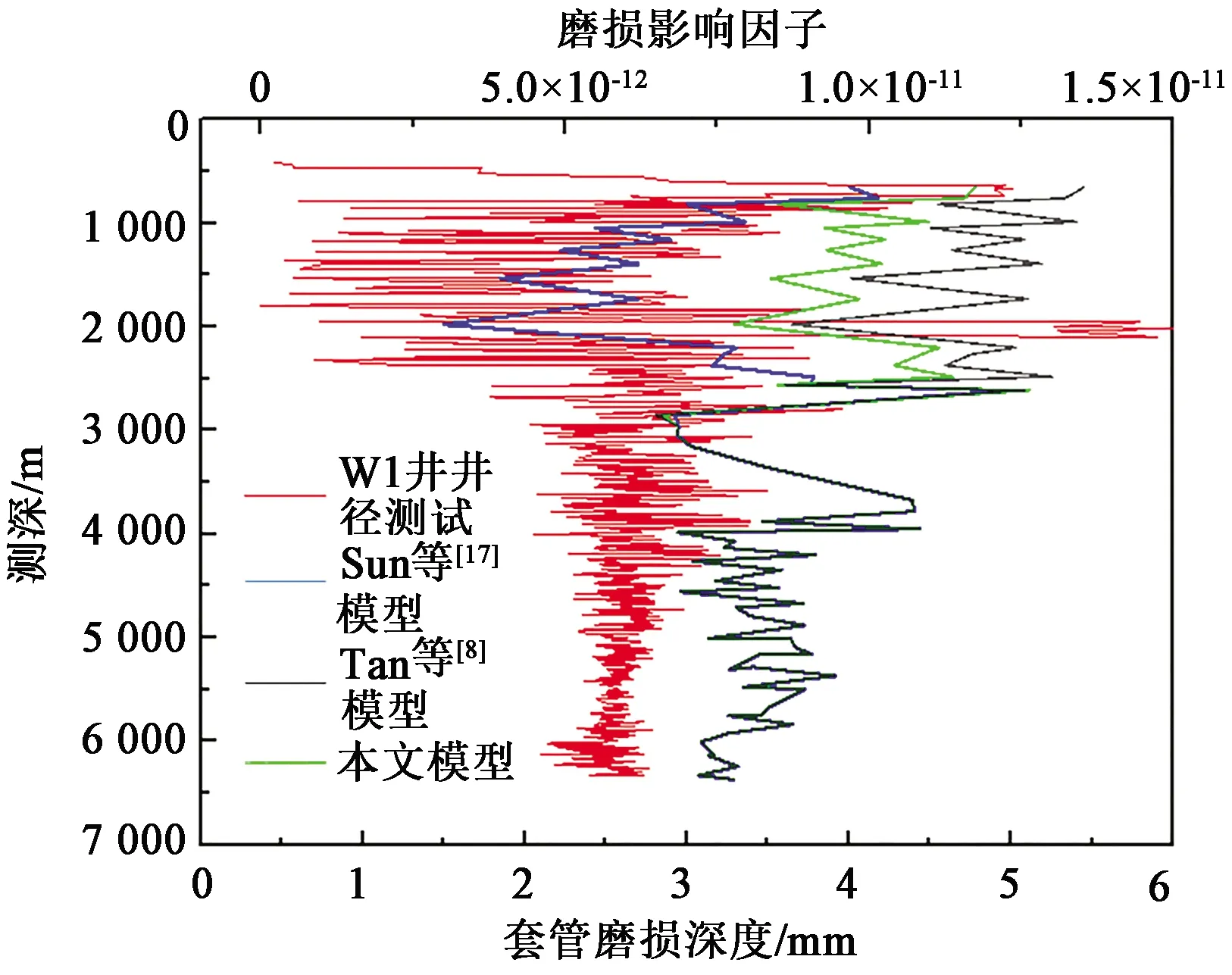
图6 W1井不同模型下的磨损影响因子反演值Fig.6 Casing wear factor inversed by different models of well W1

若只考虑钻柱屈曲引发的附加载荷、套管截面几何变形,不考虑钻柱进尺长度变化量(图6黑线),在钻柱发生屈曲的井段和屈曲位置前的井段,反演出的套管磨损影响因子fw偏大。这是由于当套管磨损深度通过井径测试确定后,钻柱进尺长度Lm越小,迭代出的fw越大,即如果认为屈曲后的钻柱轴线与井筒轴线平行,那么钻柱进尺长度Lm会被低估,反演出的fw变大,这会使目标井的套管磨损预测值不精确。

综上所述,当钻柱不发生屈曲时,本文中模型的预测结果与其他模型的预测结果相同[6,8,17];而当钻柱发生屈曲,钻柱轴线与井筒轴线不平行时,忽略钻柱进尺长度变化量会使屈曲段和屈曲段前的套管磨损影响因子反演值不精确。

4.2 套管磨损深度预测对比

基于本文中模型反演出的套管磨损影响因子,以及W2井的井眼轨道设计数据,采用不同的套管磨损预测模型对目标井W2进行套管磨损预测。

轴向摩阻系数设为0.1,周向摩阻系数设为0.25,W2井三开的钻进参数为钻压85 kN、平均机械钻速3.92 m/h、转速120 r/min。由管柱力学模型[14]计算结果可知,W2井475～750、2 200～2 600 m井深处的钻柱处于正弦屈曲状态,2 650～2 825 m井深处的钻柱处于螺旋屈曲状态,其余井深位置处的管柱未屈曲。

不同预测模型计算出的W2井套管磨损深度如图7所示。如果不考虑钻柱屈曲引发的附加载荷、套管截面几何变形和钻柱进尺长度变化量(图7黑线),计算出的屈曲段和屈曲段前的井段处的套管磨损深度值偏小,套管磨损严重程度被低估,给现场作业带来风险。

图7 W2井不同模型下的套管磨损深度预测值Fig.7 Casing wear depth calculated by different models of well W2

如果只考虑钻柱屈曲引发的附加载荷、套管截面几何变形,不考虑钻柱进尺长度变化量(图7红线),在大位移井W2的造斜段附近的套管磨损深度预测值被严重低估,其中在测深2 144 m处,套管磨损深度预测值与本文中模型预测结果(图7蓝线)相差达到最大值10.2%;如果直接忽略钻柱的屈曲效应,在测深2 144 m处,套管磨损深度预测值与本文中模型预测结果(图7蓝线)相差达到最大值16.9%。在测深大于2 800 m后,即屈曲段后的井段,本文中模型预测结果与其他模型预测结果相同。

如果钻柱不发生屈曲,即在钻柱轴线与井筒轴线平行的条件下,本文中模型的套管磨损预测结果与其他模型[6,8,17]的预测结果相同;而一旦钻柱发生屈曲,钻柱轴线与井筒轴线不平行,忽略钻柱进尺长度变化量会使屈曲段和屈曲段前的套管磨损程度被低估。

5 结 论

(1)结合南海某大位移井W1的井径测试数据,对采用“井工厂”作业模式下所钻的W2井进行了套管磨损预测,如果直接忽略钻柱的屈曲效应,在测深2 144 m处,套管磨损深度预测值误差为16.9%;如果只考虑钻柱屈曲引发的附加载荷、套管截面几何变形,不考虑钻柱进尺长度变化量,在测深2 144 m处,套管磨损深度预测值误差为10.2%。即忽略由钻柱屈曲所引起的钻柱进尺长度变化量,会使套管磨损预测值被严重低估。

(2)如果钻柱并未发生屈曲,建立的模型的计算结果与众多参考文献模型的计算结果相同。

(3)研究成果适合应用于井身结构复杂,狗腿度大的大位移井套管磨损预测,其能够降低大位移井钻井过程中的风险,为大位移井套管和钻具的选型提供依据。