双重约束非负矩阵分解与改进正交匹配追踪算法的语音增强

张开生，赵小芬

(陕西科技大学 电气与控制工程学院，陕西 西安 710021)

0 引言

语音增强是从输入语音中提取纯净的语音信号，去除无用的噪声干扰，进而提高语音的可懂度和清晰度等[1-2]。传统的语音增强方法包括维纳(Wiener)滤波[3]、谱减法[4]和最小均方差法[5]等。基于统计模型的无监督语音增强方法通常假定噪声处于一个稳定的水平，虽然可以省去训练的阶段，但是现实环境中噪声往往是非平稳的，因此传统语音增强难以满足实际需求。相较于无监督的语音增强方法，有监督模型训练的语音增强方法更能够适应实际非平稳的噪声环境[6]。非负矩阵分解(non-negative matrix factorization，NMF)[7]是近年来快速兴起的一种有监督模型的方法。文献[8]将语音存在概率融进NMF中，实现无监督语音增强，取得了一定的增强效果。文献[9]将NMF算法进行扩展，使用Kulback-Leibler(KL)实现具有监督分离效应的NMF，用以语音增强。文献[10]将心理学掩蔽特性考虑进语音增强中，并建立感知掩蔽函数，在一定程度上增强了NMF的性能。但是，目前对于NMF增强语音信号时，往往忽略了时间属性对高维矩阵分解产生的影响，并且进行NMF时，稀疏度难以控制，这些都有可能影响语音的增强性能。另外，在重构语音时，采用逆短时傅里叶变换往往没有考虑信号失真及语音可懂度差的问题，造成重构后的语音质量难以令人满意。

基于上述分析，利用NMF增强语音信号具有独特优势，但仍有改进空间。与此同时，大部分研究并未将时间约束条件考虑进去。针对上述矩阵分解稀疏度难以控制、信号重构效果不理想等问题，本文提出一种双重约束NMF与改进正交匹配追踪(orthogonal matching pursuit，OMP)算法的语音增强，采用双重约束方式改进NMF，采用改进OMP算法代替传统逆短时傅里叶变换进一步提升重构精度。通过大量的实验，证明了本文算法的有效性。

1 双重约束非负矩阵分解

1.1 基于时间约束的非负矩阵分解

文献[11]研究发现：在非负矩阵分解时，高维数据具有与时间相关的属性，然而这种属性随着降维过程损失严重，势必影响到语音增强后的性能。目前，考虑到时间属性的NMF语音增强依然匮乏。受到文献[12]的启发，本文将时间属性考虑进NMF分解中，假设第t个时间点特征向量U(t)为：

Ut≈Vt(Wt)T，

(1)

X=VW+E，

(2)

其中：E为逼近误差。矩阵X的具体分解过程为：

(3)

其中：V为基矩阵，W为系数矩阵，矩阵X中的每一列向量由基矩阵V中r个列向量的线性组合来表示，r的取值不仅影响矩阵分解后的V和W，而且还关系到低维特征的质量。考虑时间约束因素之后，r的取值同时受到维数、分解误差以及时间顺序的约束，进而将r值作为自变量，建立因变量模型为：

(4)

其中：T为具有高维属性的时间序列；r为基矩阵维度；ϖ为具有时间属性的特征维度大小。将时间点信息融合进NMF中，文献[13]采用最小化欧几里得距离的方式找到目标函数，但是采用KL散度模型来构建目标函数能提高算法的精度。因此，本文使用KL散度选取目标函数，并使目标值达到最小值。使用KL优化NMF的表达式为：

(5)

其中：i∈[1,N]；j∈[1,L]；当δ为0时，式(5)为标准的KL非负矩阵分解，按照式(5)迭代计算，就可保证将高维矩阵分解为带有时间属性的低维矩阵。

1.2 基于稀疏化约束的非负矩阵分解

在时频域中语音信号存在稀疏性，稀疏度在NMF分解成基矩阵及系数矩阵的时候，难以控制，容易造成过度拟合或残余噪声过多的情况，因此将稀疏约束系数引入，用于控制系数矩阵W的稀疏度。得到目标函数[14]为：

(6)

其中：D为目标函数；λ、γ分别为E和W的稀疏度。为了降低算法的复杂度，将正交约束表示在目标函数中，以减少计算量，得到表达式为：

(7)

其中：ζ为正交因子，采用文献[15]的更新规则。首先，将非负矩阵V和W记为：

(8)

进而有：

(9)

将最小二乘迭代规则应用于此，得到更新规则为：

(10)

其中：.*为矩阵点乘形式。

2 改进正交匹配追踪重构算法

实际上，OMP算法主要是重构出原始语音信号，但是只关注纯净语音信号，对于噪声信号来说，噪声分量会随着迭代次数的增加而增大。因此，为了保证重构语音的纯净性，必须对重构阶段加以控制，通过设置能量阈值来控制重构阶段。假设S(n)为第n帧纯净语音信号的能量，N(n)为第n帧的噪声能量，那么其能量阈值[16]可以表示为：

(11)

其中：L为总帧数；Nm(n)为第n帧的噪声能量。当恢复的能量阈值大于τ时，可认为语音分量已被提取完毕，则停止迭代。如果继续迭代，将会使部分语音信号被噪声信号所替代，降低语音增强的性能。由于OMP在进行信号重构的时候，使用最小二乘法逼近测量信号，对非线性问题求解精度低，并且使得重构后噪声信号逐渐累加，而共轭梯度法收敛快，并且可以改善矩阵求逆过程的运算量。因此，本文将OMP求解中的最小二乘法改进为共轭梯度法计算估计值，可得：

(12)

其中：αn为步长，然后不断更新步长直到共轭梯度达到n。

3 基于双重约束NMF与改进OMP算法的语音增强

输入语音信号为纯净语音信号与噪声信号的叠加：

x(t)=s(t)+n(t)，

(13)

图1 语音增强算法流程框图

其中：x(t)、s(t)和n(t)分别为输入语音信号、纯净语音信号和噪声信号。本文语音增强算法的流程框图如图1所示。

整个算法包括训练及增强两部分。在训练阶段，首先利用短时傅里叶变换(short-time Fourier transform，STFT)对纯净语音信号和噪声信号进行转换，得到幅度谱，这是因为语音信号具有短时平稳的特性，可以对其进行分帧操作。然后对每一帧进行处理，即STFT操作，STFT的表达式[17]如下：

(14)

其中：x(n)为纯净语音信号序列；ω(n)为窗函数；窗ω(n-m)会随着n取值的不同沿着时间轴滑动，经过STFT过程之后，纯净语音信号会转化为对应的幅度谱形式Xn(ejw)，同理得到噪声信号的幅度谱形式为Xn(ejw)。然后，将得到的纯净语音信号及噪声信号幅度谱经过时间及稀疏化的双重约束NMF算法，按照式(10)的更新规则进行迭代。利用NMF算法U≈VW分解为字典矩阵Vs和Vn以及激活矩阵Ws和Wn，并将Vs和Vn保存为联合字典矩阵[VsVn]，将其作为先验信息保存起来，供增强阶段使用。

增强阶段又可分为更新及语音重构。更新时，将带噪语音信号经过短时傅里叶变换得到其幅度谱形式U，并与联合矩阵结合，通过双重约束NMF进行迭代更新，直到目标函数收敛。在语音重构的部分使用改进OMP算法取代传统逆STFT进行重构，改善传统方法重构时所引起的信号失真及语音增强性能弱的缺点。使用能量阈值控制OMP算法，减少重构时引入的噪声影响，并使用共轭梯度法改进OMP，解决传统OMP使用最小二乘法收敛速度及求解精度低的问题，利用共轭梯度的快速收敛性，提高算法的效率。由于低频段为声音的集中区域，而高频区域是噪声的主要集中区域，为了有效避免重构过程中引入高频区域噪声，采用低通滤波器平滑重构语音，进而提高重构语音的可懂度与清晰度，低通滤波器的传递函数为：

(15)

其中：G为常数。

4 结果与分析

4.1 实验数据及参数设置

为了充分验证本文算法的性能，实验选取TIMIT标准语音数据集及THCHS-30中文语音数据集[18]作为实验数据来源。实验在安静的室内环境条件下进行，采样频率为16 kHz，采样大小为16 bits。从TIMIT标准语音数据库中选取240个不同人语音(其中男性120人，女性120人)共计1 200条语句，平均句长约3 s。从THCHS-30语音库中选取1.25 h的600条语音作为训练集，选择125条作为测试集。为了营造现实环境中不可避免的噪声干扰现象，引入NoiseX-92噪声库[19]作为噪声来源，选取其中的Babble、F16、Factory、Street这4种噪声作为语音信号的叠加噪声。

4.2 算法评价指标

感知语音质量评估方法(perceptual evaluation of speech quality, PESQ)是国际电信联盟(international telecommunication union，ITU)在2001年提出的一种新的语音质量客观评价算法，并且形成ITU-T的P.862建议，可以作为增强语音质量的衡量标准，并可以反映出听觉的测试结果，PESQ得分值为-0.5～4.5，在这个范围之内，得分值越高，语音质量越好。

对数谱距离(logarithmic spectral distance，LSD)用于衡量增强后的语音与纯净语音之间的对数谱距离，其数学表达式[20]为：

(16)

其中：N为帧长；L{S(l,n)}为具有一定动态范围的对数谱，可以反映重构信号与原始信号之间的差异大小，其值越小，代表与原始语音之间的差距越小，因此其与语音质量呈现出负相关的关系。

信源失真率(source distortion rate，SDR)反映增强语音信号的失真程度，其值越大，说明噪声所占比例越小，即语音增强效果越好。

对任何系统来说，时间性能都是必须考虑的因素。如果一个算法的时间复杂度过于庞大，便不能保证实时性，尤其是对于语音识别系统，良好的时间性能才能保证算法的可靠性。

4.3 对比方法及结果分析

图2 Factory背景噪声下几种语音增强方法PESQ得分值

实验中对比方法分别为单独使用NMF进行语音增强、单独OMP语音增强、正则化改进NMF的算法实现语音增强(改进NMF算法)以及改进的OMP算法实现的语音增强(改进OMP算法)。分别在-5 dB、0 dB、5 dB和10 dB这4种信噪比噪声背景下进行性能评价，并与本文算法性能指标进行比较。其中，在Factory背景噪声下得到PESQ得分情况如图2所示。由于在其他几种背景噪声下与Factory背景下所呈现的效果趋势一致，因此这里并不进行一一展示。由图2可以看出：不同算法相较于未经处理时的原始输出语音都有一定的提高，其中，本文算法的PESQ得分值均高于其他几种算法，在Factory噪声背景下，相比于未处理的情况，PESQ得分值提高41.38%；相对于传统NMF算法，PESQ得分值提高21.22%；相对于传统OMP算法，PESQ得分值提高22.93%；相较于改进NMF算法，PESQ得分值提高14.71%；相较于改进OMP算法，PESQ得分值提高15.06%。在Babble背景噪声下，本文算法相较于未经处理、传统NMF、传统OMP、改进NMF算法和改进OMP算法，其PESQ得分值分别提高37.90%、25.49%、25.76%、20.02%和20.52%。在Street背景噪声下，本文算法相较于未经处理、传统NMF、传统OMP、改进NMF算法和改进OMP算法，其PESQ得分值分别提高45.70%、34.13%、34.27%、21.02%和22.01%。在F16背景噪声下，本文算法相较于未经处理、传统NMF、传统OMP、改进NMF算法和改进OMP算法，其PESQ得分值分别提高44.78%、32.21%、29.17%、17.51%和15.98%。由上述分析可知，信噪比处于越低水平时，本文算法语音增强的效果越明显，且在不同的噪声环境下PESQ仍表现出良好的特性。这是由于本文改进了传统重构方法，使用改进OMP针对纯净语音进行重构，避免引入噪声分量引起信号失真，减少了噪声的影响。而在处于较高信噪比的情况下，由于噪声干扰较小，因此各个算法对语音增强的效果差异并不明显。

表1 不同背景噪声下几种语音增强方法LSD得分统计表

表1为在Factory、Babble、Street以及F16噪声背景下，不同方法的LSD评价。由表1可以看出：本文算法均优于其他对比算法，这与PESQ评价结果一致。本文算法LSD值均小于其他算法，说明其无论在何种噪声下，相较于对比算法，语音失真度都在减小。在处于同一类型噪声背景时，随着信噪比的提升，各个算法的LSD评价增量处于下降的趋势，说明在处于高信噪比水平时，各个算法对于LSD评价值差距不明显，这是由于在处于信噪比较高的情况下，语音失真度较小，噪声所占比例小，不同算法对于语音增强性能相差不大。在处于-5 dB Factory噪声下，本文算法的LSD评价值相较于其他5种对比方法平均下降18.81%；在Babble噪声下，LSD值平均下降23.86%；在Street噪声下，LSD值平均下降25.47%；在F16噪声下，LSD值平均下降23.90%。可见，在信噪比较低的情况下，不同的背景噪声语音失真度相较于对比算法，本文算法的LSD评价性能都有较为明显的提升。

在信噪比为-5 dB时，在4种噪声环境下，本文算法与改进NMF算法和改进OMP算法的运行时间见表2。由表2可以看出：本文算法在提高语音增强性能的前提下，并没有使系统运行时间降低，相反还有小幅度的提升。

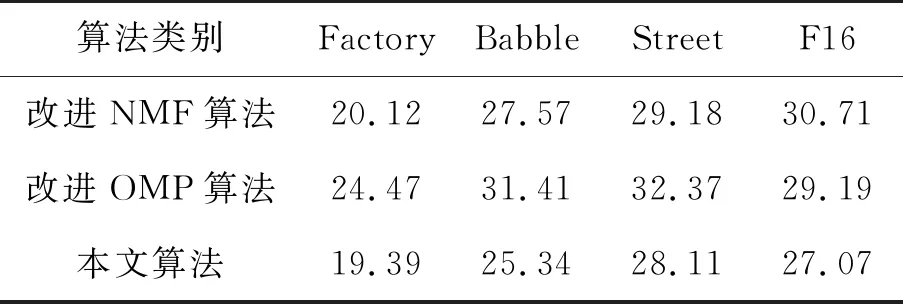
表2 本文算法与对比算法运行时间统计 s

SDR值反映了增强语音信号的失真程度，其值越大，说明噪声所占比例越小。图3为F16噪声下，不同算法的SDR值。在Factory、Babble、Street噪声环境下，不同算法的SDR值与F16噪声背景下变化趋势一致。由图3可以看出：整体上，本文算法的SDR值基本为2～14，相较于对比算法均有提高。未经任何处理的语音信号的SDR值处于较低水平，因此可以看出由于输入语音中掺杂较多的噪声信号，导致信号失真程度比较大，甚至使得SDR值为负，说明信号严重失真。传统NMF以及OMP实现的语音增强处于负信噪比时，其SDR值仍为负数，达不到语音增强的效果，而通过改进后的NMF与改进后的OMP算法的SDR值有所上升，但是仍然低于本文算法的SDR值。

图3 F16背景噪声下几种语音增强方法SDR得分值

上述从PESQ、LSD、SDR以及时间性能上验证了本文算法的有效性，为了更直观地反映增强后的语音特征，本文还采集了由自己录入的语音信息，内容为“蓝天、白云”，并作出它们对应的语谱图，由于整体而言改进NMF算法相较于改进OMP算法的性能略优，因此选取改进NMF算法与本文算法进行语谱图比较，如图4a和图4b所示。图4a为本文算法对应的语谱图，图4b为改进NMF算法的语谱图。根据语谱图颜色来评判语音增强状况，颜色越深表明对应语音频谱能量越强。由图4可以看出：本文算法增强后语音的语谱图比改进NMF算法更加清晰，对于噪声的抑制效果更好。

(a) 本文算法

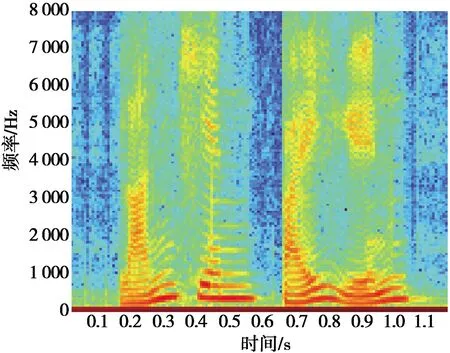
(b) 改进NMF算法

5 结束语

(1)采用时间约束及稀疏度约束的方式改进NMF算法，克服了传统NMF算法未考虑时间属性对于高维信号分解的影响以及分解时稀疏度难以控制的问题。

(2)采用改进OMP算法代替传统逆短时傅里叶变换，提升了算法的重构精度。为了进一步平滑滤波，引入低通滤波器。

(3)综合PESQ、LSD、SDR以及时间性能4种指标，本文算法评价指标均优于对比算法。并且当信噪比处于低水平(小于0 dB)时，在不同的噪声环境下，都具有良好的增强效果，显示出本文算法较强的适应能力。