THE UNIQUENESS OF THE LpMINKOWSKI PROBLEM FOR q-TORSIONAL RIGIDITY∗
Guangling SUN(孙广玲) Lu XU (徐露) Ping ZHANG (章萍)
School of Mathematics,Hunan University,Changsha 410082,China
E-mail:sgl275869080@hnu.edu.cn;xulu@hnu.edu.cn;zping071727@hnu.edu.cn
Abstract In this paper,we prove the uniqueness of the LpMinkowski problem for qtorsional rigidity with p>1 and q>1 in smooth case.Meanwhile,the LpBrunn-Minkowski inequality and the LpHadamard variational formula for q-torsional rigidity are established.
Key words q-torsional rigidity;LpMinkowski problem;LpHadamard variational formula;LpBrunn-Minkowski inequality
1 Introduction
The setting of this article is the n-dimensional Euclidean space Rn.A convex body in Rnis a compact convex set with nonempty interiors.The Brunn-Minkowski theory forms the classical core of the geometry of convex bodies.A series of works by Brunn and Minkowski laid the foundation for the Brunn-Minkowski theory.After that,it was developed by the research work of Aleksandrov,Fenchel,and many other scholars.The concerns of this theory are the geometric functionals of convex bodies and the differentials of these functionals.In general,differentiating these functionals produces new geometric measures.
The Minkowski problem holds an important position in Brunn-Minkowski theory.It is a feature problem for those geometric measures arising from convex bodies.It asks:what are the necessary and sufficient conditions for a given measure to be the measure which is generated by a convex body?For example,in the case when the geometric functional is volume,the Minkowski problem is the classical Minkowski problem.When we differentiate the volume,it yields the surface area measure.Usually,when convex bodies are smooth,formulating the Minkowski problem can be transformed into solving a fully nonlinear partial differential equation on the unit sphere.So far,research on the classical Minkowski problem has been remarkable;see Aleksandrov[1,2],Lewy[20],Fenchel-Jessen[14],Nirenberg[24],Cheng-Yau[9],Pogorelov[25],Caffarelli[7],etc..We also note that the Minkowski problem for electrostatic capacity was solved by Jerison[19]for existence,and by Caffarelli-Jerison-Lieb[8]for uniqueness.Twenty years later,the Minkowski problem for q-capacity was studied by Colesanti-Nystr¨om-Salani-Xiao-Yang-Zhang[13]and Akman-Gong-Hineman-Lewis-Vogel[4].
In 1962,Firey[15]introduced the Lpsum of convex bodies.Using the Lpcombination,Lutwak[22]initiated the LpMinkowski problem for volume,which is the classical Minkowski problem when p=1.Thus,the LpMinkowski problem is a generalization of the Minkowski problem when the Minkowski linear addition is extended to an Lpsum.The LpMinkowski problem for volume and q-capacity has been well studied.For the former,one can see Andrews[3],Lutwak[22],Lutwak-Yang-Zhang[23],Chou-Wang[10],Brczky-Lutwak-Yang-Zhang[6],Xiong-Li[27],Zhu[29]and references therein.We refer to Xiong-Xiong-Xu[28],Lu-Xiong[21],Zou-Xiong[31]for the latter.Compared with the large number of remarkable results on the LpMinkowski problem for volume and capacity,there are few studies on the LpMinkowski problem for q-torsional rigidity.
1.1 q-torsional rigidity,q-torsional measure
In what follows,we introduce the de finition of q-torsional rigidity and its corresponding measure.Denote by Sn−1the unit sphere in Rn.Denote by Knthe set of convex bodies in Rn.Writefor the set of convex bodies with the origin o in their interiors.
Let q>1 and Ω be the interior of convex body K.We introduce the well-known functional τq(K),called the q-torsional rigidity of K,by the following formula(see[11]):
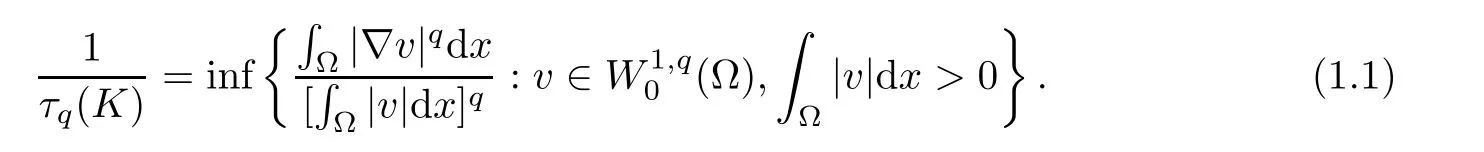
The functional de fined in(1.1)admits a minimizer u∈,and cu(for some constant c)is the unique positive solution of the following boundary value problem(see[5]and[17]):
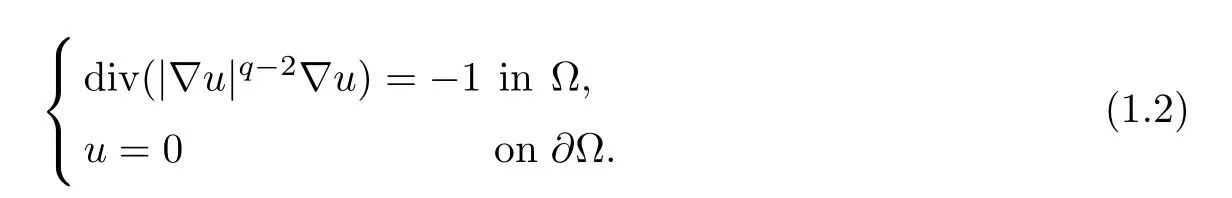
For Borel set E⊂Sn−1,we de fine the q-torsional measureµq(Ω,·)by(see[18])

Thusµq(K,·)can be regarded as the differential of the q-torsional rigidity functional from formula(1.4).
1.2 L p q-torsional measure and the L p Minkowski problem for q-torsional rigidity
De finition 1.1Let p∈R and q>1.For K∈,the Lpq-torsional measureµp,q(K,·)of K is a finite Borel measure de fined,for each Borel set ω⊆Sn−1,by

whereµqis q-torsional measure de fined in(1.3).
We pose the following LpMinkowski problem for q-torsional rigidity:
LpMinkowski problem for q-torsional rigidity.Supposing that q>1,p∈R andµis a finite Borel measure on Sn−1,what are the necessary and sufficient conditions onµso thatµis the Lpq-torsional measureµp,q(K,·)of a convex body K in?
For the classical case p=1,i.e.,the Minkowski problem for q-torsional rigidity,there are few results.Colesanti and Fimiani[12]proved the existence and uniqueness of the solution when q=2.Very recently,Huang-Song-Xu[18]proved the Hadamard variational formula for general q,which is the first step in solving the Minkowski problem.The main goal of this paper is to solve the uniqueness of the LpMinkowski problem for q-torsional rigidity for p>1 in the smooth case.
We say that a convex body K is of classif its boundary is C2,α-smooth,for some α∈(0,1),and of positive Gauss curvature.Throughout the rest of the paper we assume that all convex bodies are of.
Theorem 1.2Suppose that q>1,p>1 and K,L∈.If K and L have the same Lpq-torsional measure,then K=L when p−n,and K and L are dilates when p−=n.
This paper is organized as follows:in Section 2,we introduce some necessary notations and basic facts on convex bodies and q-torsional rigidity.In Section 3,the uniqueness of the LpMinkowski problem for q-torsional rigidity when p>1 is proved.At the same time,in Section 3,we obtain some key results on the Lpq-torsional measure:the LpBrunn-Minkowski inequality,the LpHadamard variational formula of q-torsional rigidity,and the LpMinkowski inequality for q-torsional rigidity.
2 Preliminaries
2.1 Basic facts on convex bodies
In this part,we list some basic facts on convex bodies;see for example Gruber[16]and Schneider[26].
Letting x,y∈Rn,write x·y for the standard inner product.A convex body K in Rnis uniquely determined by its support function hK:Rn→R,de fined for x∈Rnby
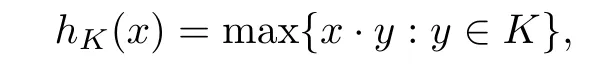
which is usually restricted to the space Sn−1.
Convex bodies K and L are said to be homothetic if K=sL+x for some s>0 and x∈Rn.The Minkowski sum of K and L is the set K+L={x+y:x∈K,y∈L}.For s>0,the set sK={sx:x∈K}is called a dilate of K.

2.2 Basic facts on q-torsional rigidity
In what follows we set˜τ=˜τq,for simplicity.


This yields(2.2).Furthermore,the equality holds if and only if K and L are homothetic,thanks to the equality condition in Brunn-Minkowski inequality(3.7)in[18].
3 Uniqueness of LpMinkowski Problem for q-torsional Rigidity
3.1 LpBrunn-Minkowski inequality for˜τ
For p=1,we know the Brunn-Minkowski inequality from equation(3.7)in[18]with equality if and only if K and L are homothetic.
In what follows,the LpBrunn-Minkowski inequality forand its equality conditions were obtained for p>1.The proof is similar to that of Theorem 3.1 in[30].
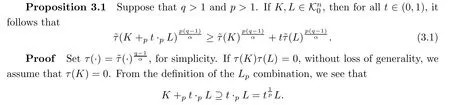
Thus the monotonicity and positive homogeneity of τ(Lemma 2.1)gives that
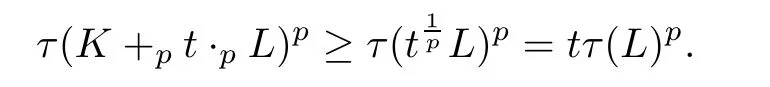
Then(3.1)holds.

Hence,from(3.4),(3.5)and the monotonicity of τ,the Brunn-Minkowski inequality(2.3),and the positive homogeneity of τ,we have
Then he gave his good wishes for the journey and his blessing80, and the prince kissed his Bet, said good-bye, and, with thanks to the Causer of Causes, took the road
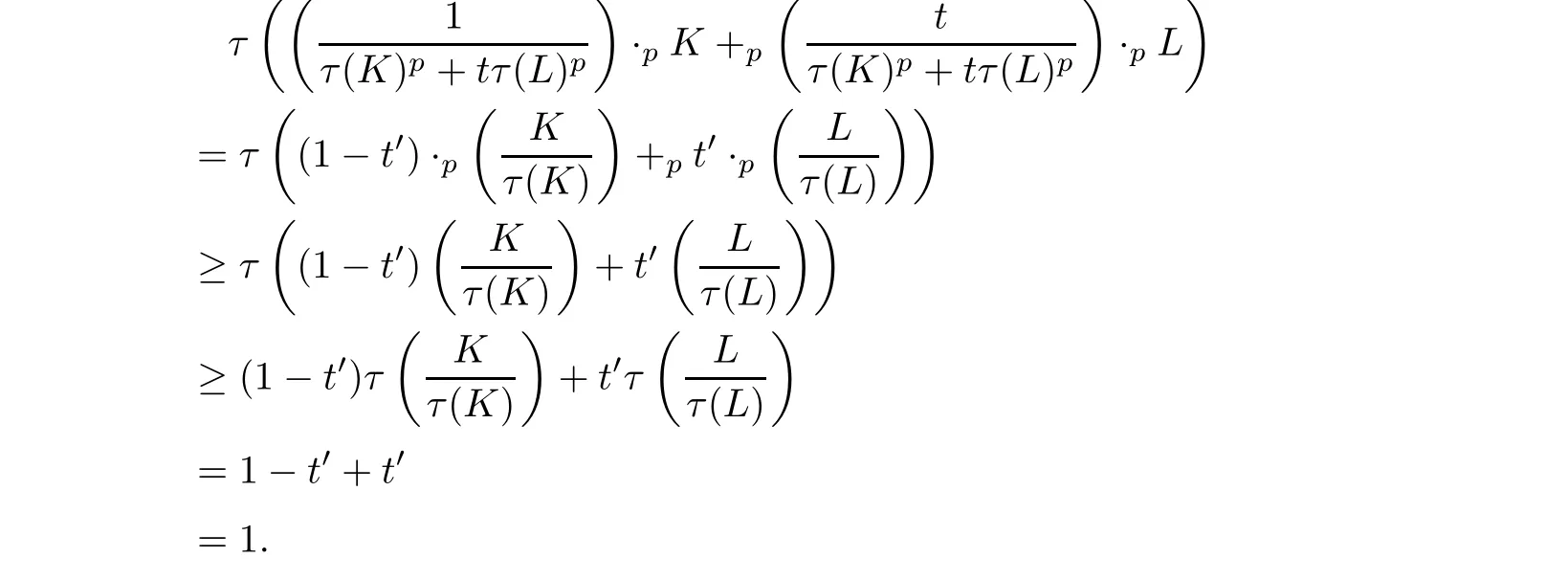
Therefore,inequality(3.3)holds,that we have inequality(3.1).
Next,in a fashion similar to the proof of Theorem 3.5 in[30],we can obtain the equality conditions in the inequality(3.1).
Proposition 3.2For K,L∈,the equality in(3.1)holds if and only if K and L are dilates.
ProofSet τ(·)=˜τ(·)q−1α,for simplicity.Notice that τ is positively homogenous,increasing and translation invariant,according to Lemma 2.1.
Suppose that the conclusion of this proposition is not true,and that there exist t0∈(0,1),K0,L0∈,which are not dilates,such that the equality in(3.1)holds,i.e.,that
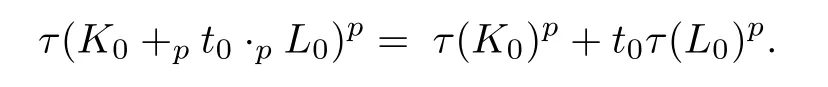
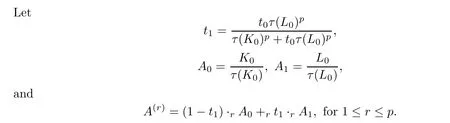
Obviously,τ(A0)=τ(A1)=1.On one hand,from the assumption,we have that
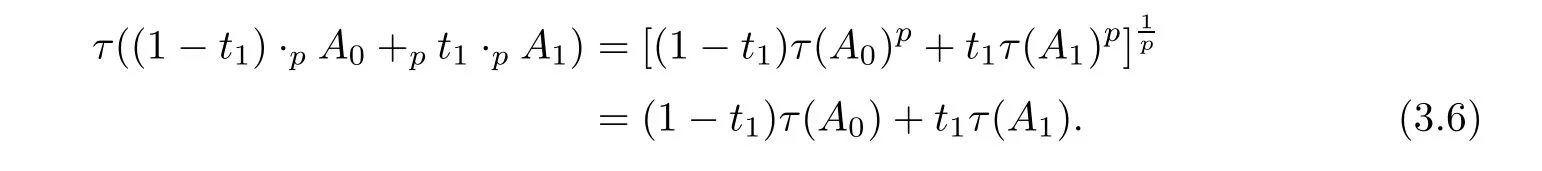
On the other hand,by Lemma 2.2 in[30]and the monotonicity of τ and(2.3),we have that
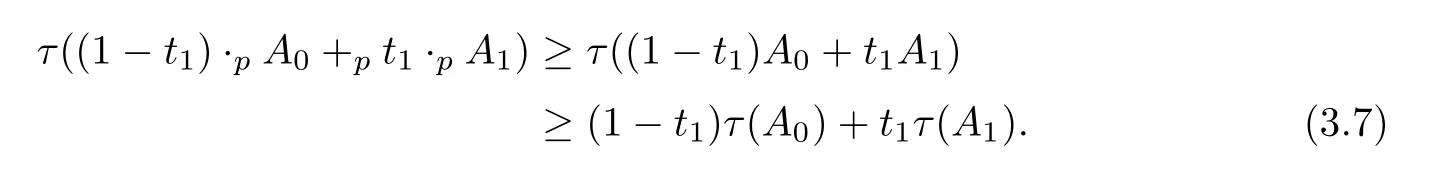
Therefore,(3.6)and(3.7)give that
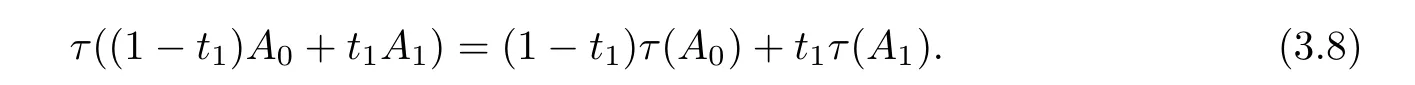
Obviously,by the equality condition in(2.3),we have that(3.8)holds if and only if K and L are homothetic.That is,there exist λ0>0 and x0∈Rnsuch that
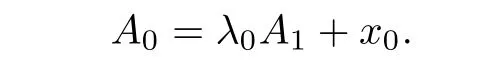
Meanwhile,from the positive homogeneity and translation invariance of τ,it follows that

Thus,λ0=1 and A0=A1+x0.
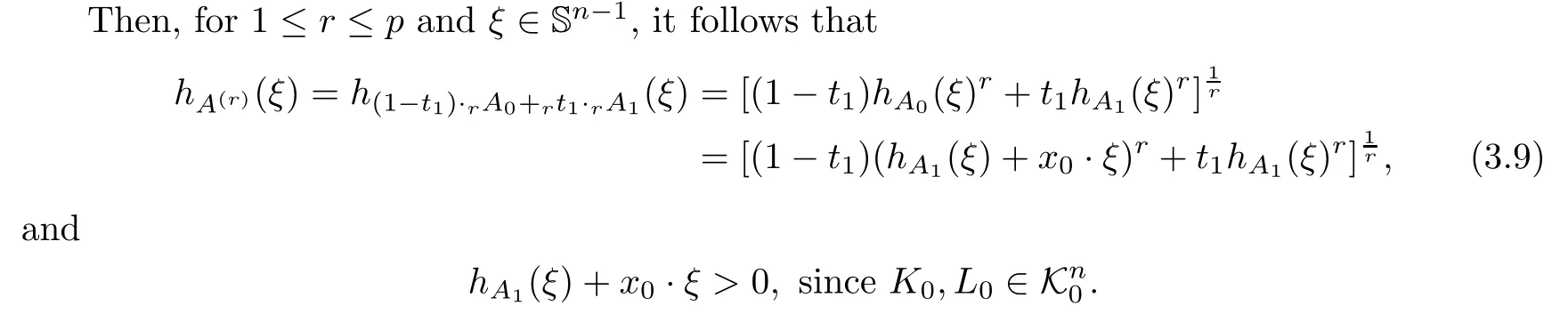
Now,for ξ∈Sn−1,we have two observations.
First,if x0·ξ=0,then for 1≤r1≤r2≤p,we have
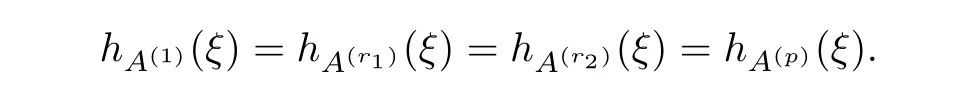
Second,if x0·ξ0,then from the strict concavity of power functions,for 1 Therefore,for 1≤r1≤r2≤p,we have that On the one hand,by(a),for θ∈(0,1),we have On account of the monotonicity of τ,this yields On the other hand,from(3.6)and(3.8),it follows that Thus,by the equality condition in(2.3),A(1)and A(p)are homothetic,which contradicts(b). Therefore,the assumption at the beginning is wrong.The proof is finished. In what follows,in a way similar to the proof of Lemma 5.1 in[13],we obtain the Lpfirst variational formula for q-torsional rigidity. In this part,we prove the LpMinkowski inequality for q-torsional rigidity combining Propositions 3.1,3.2 and 3.3 together.The inequality is the key to proving our main results. In this part,by using Theorem 3.5,we show two theorems that can be used to prove Theorem 1.2.Then we can conclude the uniqueness of solutions to the Lpq-torsional Minkowski problem. equality holds if and only if K,L are dilates.This inequality is reversed by interchanging K and L.Then we deduce that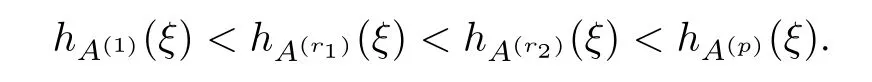
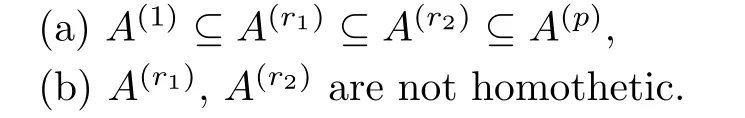

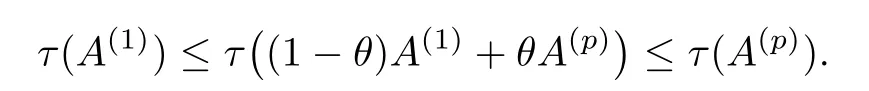
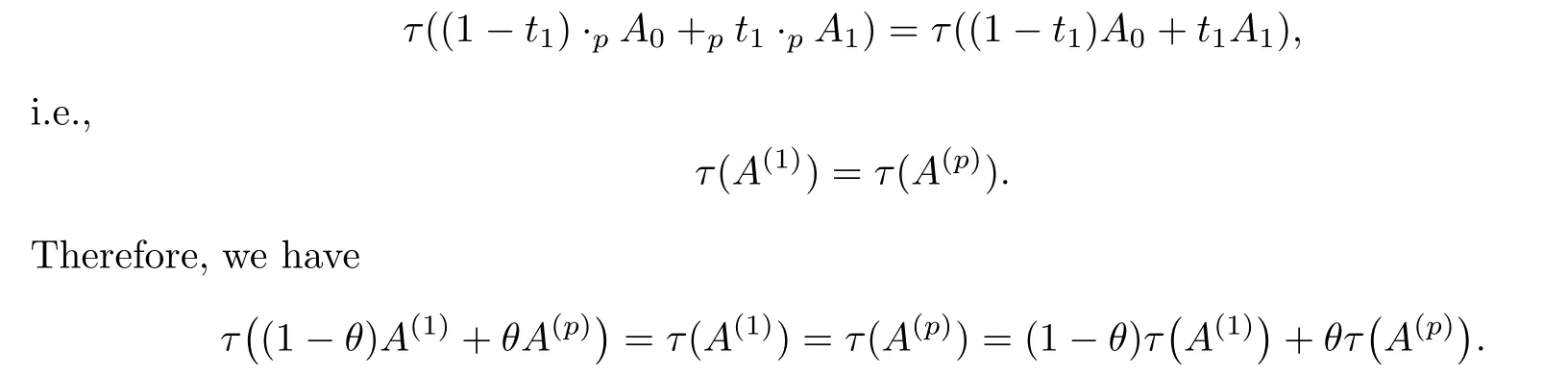
3.2 The LpHadamard variational formula for q-torsional rigidity


3.3 The LpMinkowski inequality for q-torsional rigidity

3.4 The uniqueness of the Lpq-torsional measure

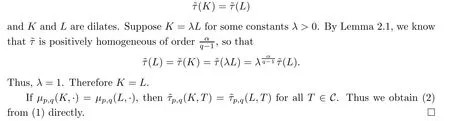

 Acta Mathematica Scientia(English Series)2021年5期
Acta Mathematica Scientia(English Series)2021年5期
- Acta Mathematica Scientia(English Series)的其它文章
- HYERS–ULAM STABILITY OF SECOND-ORDER LINEAR DYNAMIC EQUATIONS ON TIME SCALES∗
- ON NONCOERCIVE(p,q)-EQUATIONS∗
- THE CONVERGENCE OF NONHOMOGENEOUS MARKOV CHAINS IN GENERAL STATE SPACES BY THE COUPLING METHOD∗
- POSITIVE SOLUTIONS OF A NONLOCAL AND NONVARIATIONAL ELLIPTIC PROBLEM∗
- A PENALTY FUNCTION METHOD FOR THE PRINCIPAL-AGENT PROBLEM WITH AN INFINITE NUMBER OF INCENTIVE-COMPATIBILITY CONSTRAINTS UNDER MORAL HAZARD∗
- THE INITIAL BOUNDARY VALUE PROBLEMS FOR A NONLINEAR INTEGRABLE EQUATION WITH 3×3 LAX PAIR ON THE FINITE INTERVAL∗
