ON NONCOERCIVE(p,q)-EQUATIONS∗
Nikolaos S.PAPAGEORGIOU
Department of Mathematics,National Technical University,Zografou Campus,15780,Athens,Greece
E-mail:npapg@math.ntua.gr
Calogero VETRO
Department of Mathematics and Computer Science,University of Palermo,Via Archira fi34,90123,Palermo,Italy
E-mail:calogero.vetro@unipa.it
Francesca VETRO†
90123,Palermo,Italy
E-mail:francescavetro80@gmail.com
Abstract We consider a nonlinear Dirichlet problem driven by a(p,q)-Laplace differential operator(1 Key words (p,q)-Laplacian;principal eigenvalue;constant sign and nodal solutions;extremal solutions;nonlinear regularity Let Ω⊆RNbe a bounded domain with a C2-boundary∂Ω.In this paper we study the following(p,q)-Dirichlet problem: In this problem 1 The reaction f(z,x)is a Carath´eodory function,that is,for all x∈R z→f(z,x)is measurable and for a.a.z∈Ω x→f(z,x)is continuous.We assume that f(z,·)exhibits(p−1)-linear growth at±∞(that is,f(z,·)is(p−1)-homogeneous at±∞).However,the problem is noncoercive since asymptotically as x→±∞the quotientstays above the principal eigenvalueSimilarly asymptotically as x→0,the quotientstays aboveHence the origin can not be a local minimizer of the energy functional and this does not permit the use of the mountain pass theorem directly on the energy functional.Nevertheless by assuming an oscillatory behavior of f(z,·)near zero,and using variational methods based on the critical point theory together with suitable truncation and comparison techniques and with the use of critical groups(Morse theory),we prove two multiplicity theorems producing five and six nontrivial smooth solutions respectively,all with sign information.Coercive(p,q)-equations were studied by Papageorgiou-R˘adulescu-Repovˇs[18],Papageorgiou-Vetro-Vetro[21](with q=2),Marano-Papageorgiou[15]and Medeiros-Perera[16].In these works the authors prove the existence of three or four nontrivial solutions,and nodal solutions(that is,sign changing solutions)were obtained only in[17,20].Noncoercive(p−1)-linear equations were investigated by Cingolani-Degiovanni[2]and Papageorgiou-R˘adulescu-Repovˇs[18,19].In[2]we find only an existence result,while in[18,19]q=2 and the equation is parametric.The authors produce up to four solutions for small values of the parameter.Our work complements that of Gasi´nski-Papageorgiou[7],where an analogous multiplicity theorem is proved for equations driven by the p-Laplacian only and with a reaction which satis fies more restrictive conditions and no nodal solutions are obtained.Finally we mention the recent works of He-Lei-Zhang-Sun[10](with q=2 and(p−1)-superlinear reaction)and of Papageorgiou-Vetro-Vetro[22](also with q=2,parametric concave-convex problems). We mention that for both eigenvalue problems(2.1)and(2.3),only the first eigenvalue has eigenfunctions of constant sign.All the other eigenvalues have eigenfunctions which are nodal(sign changing). Let X be a Banach space and ϕ∈C1(X,R).By Kϕwe denote the critical set of ϕ,that is, Also,if c∈R,then we set We say that ϕ∈C1(X,R)satis fies the“C-condition”,if the following holds: “Every sequence{un}n≥1⊆X such that{ϕ(un)}n≥1⊆R is bounded and admits a strongly convergent subsequence”. This is a compactness-type condition on the functional ϕ(·)which compensates for the fact that the ambient space X is not locally compact(being in general in finite dimensional). Let(Y1,Y2)be a topological pair such that Y2⊆Y1⊆X.For every k∈N0,by Hk(Y1,Y2)we denote the kth-relative singular homology group with integer coefficients for the pair(Y1,Y2).Then the critical groups of ϕ(·)at an isolated u∈Kϕwith c=ϕ(u),are de fined by with U being a neighborhood of u such that The excision property of singular homology implies that the above de finition of critical groups is independent of the isolating neighborhood U. Suppose that ϕ satis fies the C-condition and inf ϕ(Kϕ)>−∞.Let c The second deformation theorem(see Papageorgiou-R˘adulescu-Repov[20],Theorem 5.3.12,p.386)implies that this de finition is independent of the choice of the level c Assume that Kϕis finite.We set Then the Morse relation says that Finally given h1,h2∈L∞(Ω),we write h1≺h2if for all K⊆Ω compact,there exists cK>0 such that If h1,h2∈C(Ω)and h1(z) Also for k,n∈N0,by δk,nwe denote the Kronecker symbol de fined by In this section we produce constant sign smooth solutions for problem(1.1).The hypotheses on the reaction f(z,x)are the following: H1:f:Ω×R→R is a Carathodory function such that f(z,0)=0 for a.a.z∈Ω and (i)|f(z,x)|≤a(z)[1+|x|p−1]for a.a.z∈Ω,all x∈R,with a∈L∞(Ω); (ii)there exists a function η∈L∞(Ω)such that (iii)there exists a function η0∈L∞(Ω)such that is nondecreasing on[−ρ,ρ]. Remark 3.1Hypotheses H1(iii),(iv)imply that f(z,·)has an oscillatory behavior near zero.Hypothesis H1(v)is a one-sided local Lipschitz condition and it is satis fied if for a.a.z∈Ω,f(z,·)is differentiable and for every ρ>0,we can find>0 such that First using only the growth condition H1(i)and the local conditions near zero H1(iii),(iv),we will produce two nontrivial constant sign smooth solutions. Proposition 3.2If hypotheses H1(i),(iii),(iv)hold,then problem(1.1)has two constant sign solutions ProofFirst we produce the positive solution.To this end,we introduce the Carathodory function(z,x)de fined by Invoking Theorem 7.1,p.286,of Ladyzhenskaya-Ural′tseva[12]we have that u0∈L∞(Ω).Then the nonlinear regularity theory of Lieberman[14]implies that u0∈C+{0}.On account of hypotheses H1(i),(iii),given ε>0,we can find c3=c3(ε)>0 such that Since q is nondecreasing on[0,δ].Then(3.7),(3.8)and Theorem 5.4.1,p.111,of Pucci-Serrin[23]imply that Finally invoking the nonlinear boundary point theorem(see Pucci-Serrin[23],Theorem 5.5.1,p.120),we have Invoking Proposition 3.2 of Gasi´nski-Papageorgiou[9]we obtain For the negative solution,we introduce the Carath´eodory functionde fined by Now using u0,v0from the above proposition and making use also of hypothesis H1(ii)(the asymptotic condition as x→±∞),we will generate two more nontrivial constant sign smooth solutions of(1.1),which are localized with respect to u0and v0. Proposition 3.3If hypotheses H1(i)–(iv)hold,then problem(1.1)has two more constant sign solutions∈intC+and∈−intC+such that ProofFirst we produce the second positive solution. Let u0∈intC+be the positive solution produced in Proposition 3.2.We introduce the Carath´eodory function g+(z,x)de fined by From(3.10)and hypothesis H1(i),we have Hence we have From(3.17),hypothesis H1(ii)and by passing to a subsequence if necessary we have In(3.16)we choose h=yn−y∈(Ω),pass to the limit as n→+∞and use(3.15),(3.18)and(3.14).We obtain If in(3.16)we pass to the limit as n→+∞and use(3.18),(3.19)and(3.14)(recall q From(3.20)and(3.21)it follows that y must be nodal,a contradiction(see(3.19)).This means that So,we may assume that In(3.12)we choose h=un−u∈pass to the limit as n→+∞and use(3.16).Then So ψ+(·)satis fies the C-condition and this proves Claim 1. Using(3.10)and the nonlinear regularity theory(see Lieberman[14]),we obtain that Without any loss of generality,we may assume that Otherwise we already have a second positive smooth solution bigger than u0and so we are done. Claim 2u0is a local minimizer of the functional ψ+(·). Consider the following truncation of g+(z,·): This proves Claim 2. From(3.23)it is clear that we may assume that Otherwise we already have an in finity of positive smooth solutions of(1.1)which are bigger than u0. From Claim 2,(3.29)and Theorem 5.7.6,p.449,of Papageorgiou-R˘adulescu-Repov[20],we know that we can find ρ∈(0,1)small such that On account of hypotheses H1(i),(ii)and(3.10),we see that given ε>0 we can find c7=c7(ε)>0 such that Next we will show that problem(1.1)admits extremal constant sign solutions,that is,a smallest positive solution u∗∈intC+and a biggest negative solution v∗∈−intC+.In Section 4 we will use these extremal constant sign solutions in order to produce a nodal solution for problem(1.1). To produce the extremal constant sign solutions,we need to do some preparatory work.Hypotheses H1(i),(ii)imply that given ε>0,we can find c10=c10(ε)>0 such that Motivated by this unilateral growth condition on the reaction f(z,·),we introduce the following auxiliary Dirichlet(p,q)-problem Proposition 3.4For all ε>0 small,problem(3.36)admits a unique positive solution∈intC+and since the problem is odd,=−∈−intC+is the unique negative solution of(3.36). ProofFirst we prove the existence of a positive solution for problem(3.36)when ε>0 is small. This proves the uniqueness of the positive solution∈intC+of problem(3.36).Since the problem is odd,=−∈−intC+is the unique negative solution of(3.36). Let S+(resp.S−)be the set of positive(resp.negative)solutions of problem(1.1).We know that Proposition 3.5If hypotheses H1hold,then≤u for all u∈S+and v≤for all v∈S−. ProofLet u∈S+and consider the Carathodory function k+(z,x)de fined by Then from(3.41),(3.38),(3.40),we infer thatis a positive solution of problem(3.36).Therefore=∈intC+(see Proposition 3.4).So,we have Now we are ready to produce the extremal constant sign solutions of problem(1.1).As we already mentioned,in Section 4 using these solutions,we will be able to produce a nodal solution. Proposition 3.6If hypotheses H1hold,then problem(1.1)admits extremal constant sign solutions,that is, •there exists u∗∈S+such that u∗≤u for all u∈S+; •there exists v∗∈S−such that v≤v∗for all v∈S−. ProofFrom Filippakis-Papageorgiou[4]we know that S+is downward directed(that is,if u1,u2∈S+,then we can find u∈S+such that u≤u1,u≤u2).Invoking Lemma 3.10,p.178,of Hu-Papageorgiou[11],we can find{un}n≥1⊆S+decreasing such that In this section using the extremal constant sign solutions produced in Proposition 3.5 and by strengthening the condition on f(z,·)near zero,we produce a nodal solution. The new hypotheses on the reaction f(z,x)are the following: H2:f:Ω×R→R is a Carath´eodory function such that f(z,0)=0 for a.a.z∈Ω,hypotheses H2(i),(ii),(iv),(v)are the same as the corresponding hypotheses H1(i),(ii),(iv),(v)and Remark 4.1Evidently hypothesis H2(iii)is more restrictive than hypothesis H1(iii).Note that H1(iii)allowed nonlinearities with(p−1)-linear growth near zero.Under hypothesis H2(iii)this is no longer possible. Example 4.2The following function satis fies hypotheses H2(for the sake of simplicity we drop the z-dependence): ProofLet u∗∈intC+and v∗∈−intC+be the two extremal constant sign solutions of(1.1)produced in Proposition 3.6.We introduce the Carath´eodory function w(z,x)de fined by Also we consider the positive and negative truncations of w(z,·),namely the Carathodory functions So,from(4.11)and Proposition 3.2 of Gasi´nski-Papageorgiou[9],we have In a similar fashion,we show that We conclude that We can state the following multiplicity theorem for problem(1.1). Theorem 4.4If hypotheses H2hold,then (a)problem(1.1)admits at least five nontrivial solutions (b)problem(1.1)admits extremal constant sign solutions (that is,u∗≤u for all u∈S+=set of positive solutions of(1.1)and v≤v∗for all v∈S−=set of negative solutions of(1.1)). Remark 4.5We point out that in the above theorem,not only we provide sign information for all the solutions produced,but the solutions are also ordered(that is,≤v0≤≤u0≤).In the above theorem the nodal solution was obtained at the expense of requiring that f(z,·)is strictly(q−1)-sublinear near zero(presence of a concave term near zero,see hypothesis H2(iii)).If q=2,then we can treat also the case of linear growth near zero.This is done in the next section using critical groups. In this section we deal with the following particular case of problem(1.1): The hypotheses on the reaction f(z,x)are the following: H3:f:Ω×R→R is a measurable function such that for a.a.z∈Ω f(z,0)=0,f(z,·)∈C1(R)and (ii)there exist a function η∈L∞(Ω)and c∞>‖η‖∞such that Remark 5.1Hypothesis H3(iii)dictates a linear growth for f(z,·)near zero.This is in contrast to hypothesis H2(iii).In that hypothesis we required that f(z,·)is strictly(q−1)-sublinear near zero. Proposition 5.2If hypotheses H3hold,then problem(5.1)has at least two nodal solutions ProofReasoning as in the proof of Proposition 4.3 and since m≥2,we produce a solution This solution is obtained via an application of the mountain pass theorem(see the proof of Proposition 4.3).Therefore The norm continuity of critical groups(see Papageorgiou-Rdulescu-Repov[20],Theorem 6.3.4,p.503),implies that Since dm≥2,from(5.4)and(5.7)it follows that Recall that u∗and v∗are local minimizers of(see(5.6),(5.7)).Hence we have Therefore for problem(5.1)we can state the following multiplicity theorem. Theorem 5.3If hypotheses H3hold,then (a)problem(5.1)admits at least six nontrivial solutions (b)problem(5.1)admits extremal constant sign solutions1 Introduction
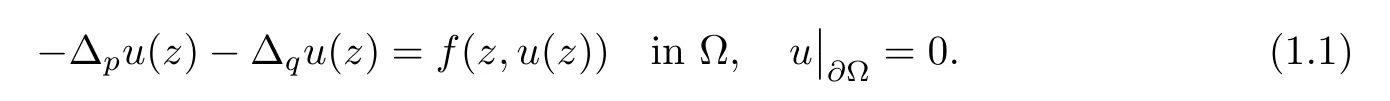

2 Mathematical Background


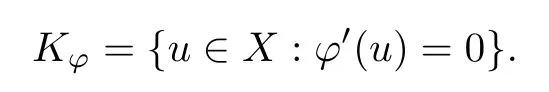

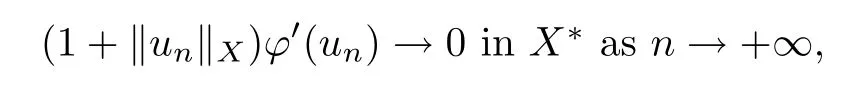
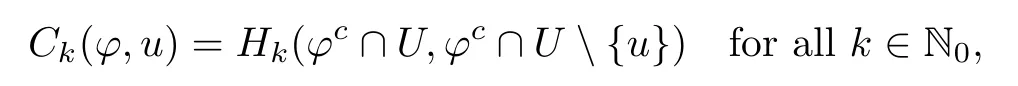
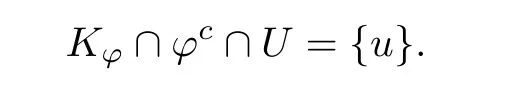
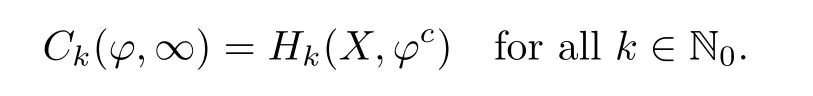
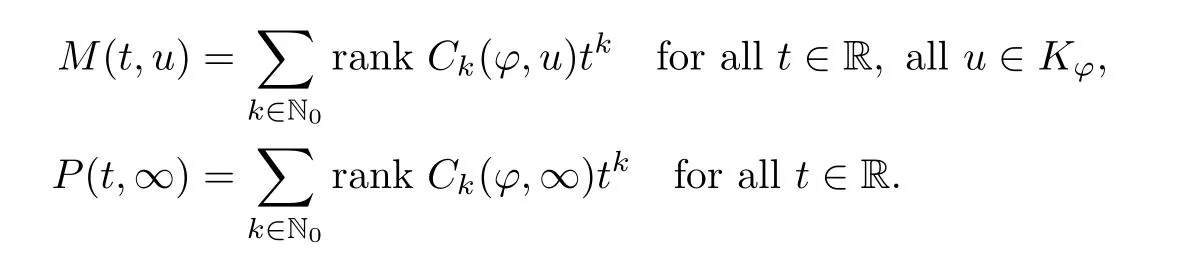

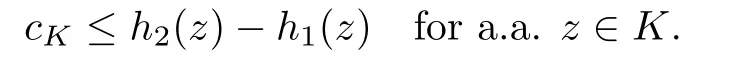
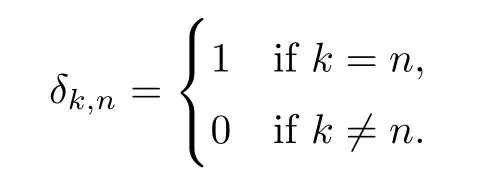
3 Constant Sign Solutions
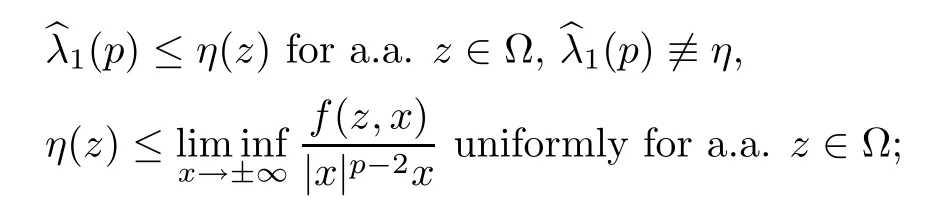
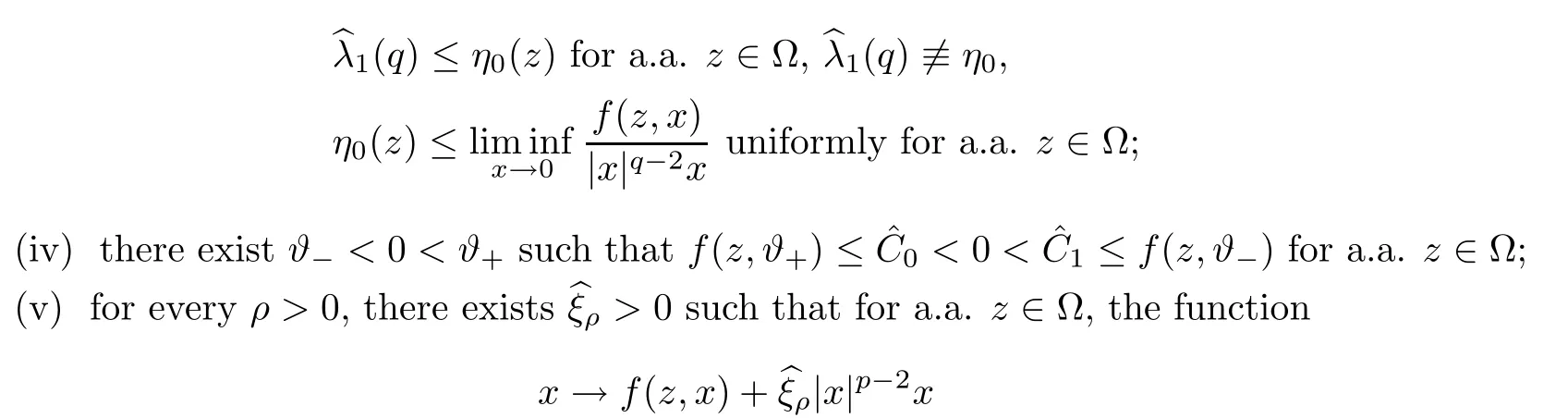
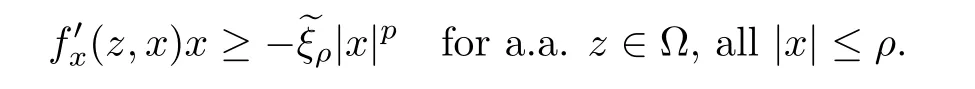
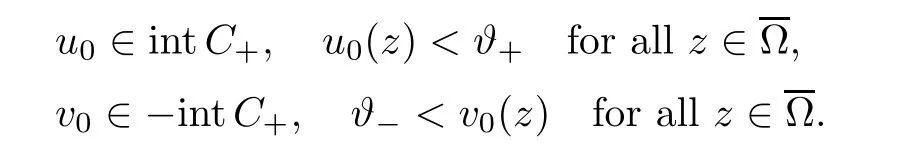

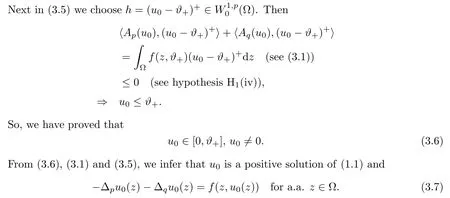
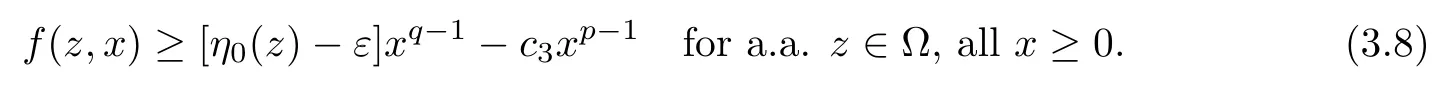

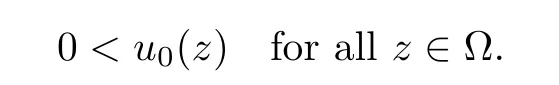

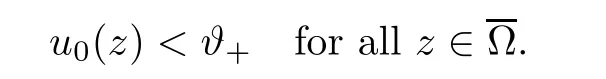
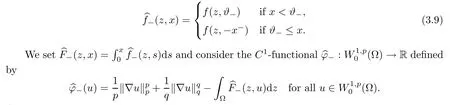
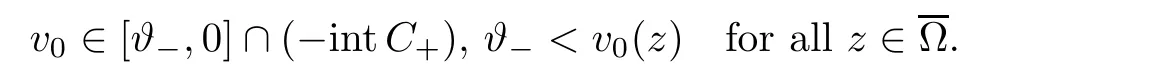

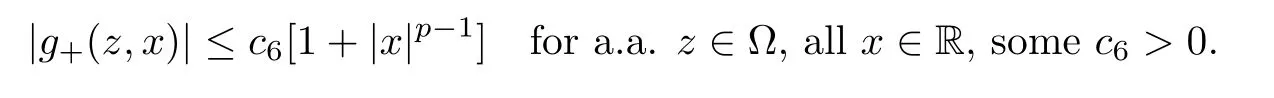
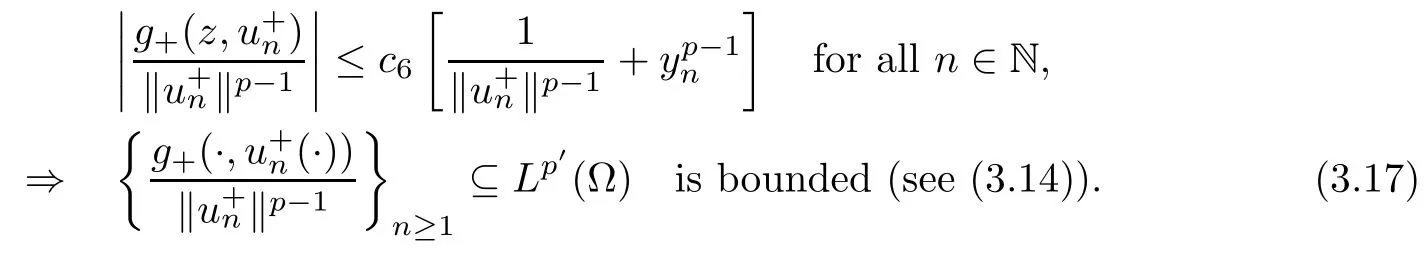
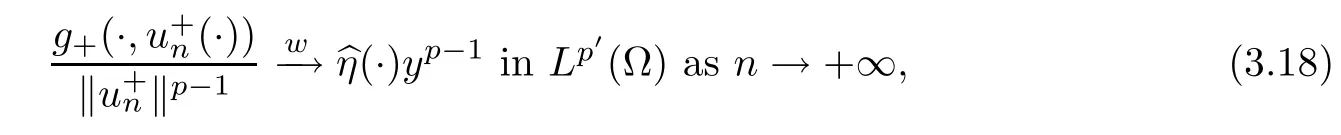



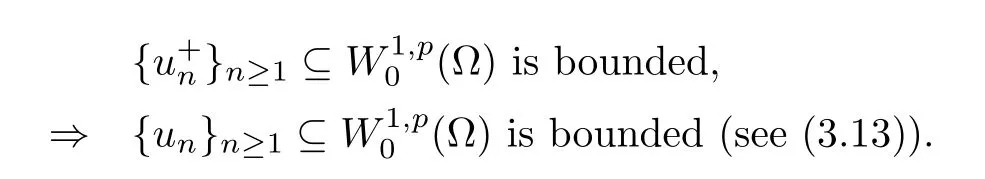
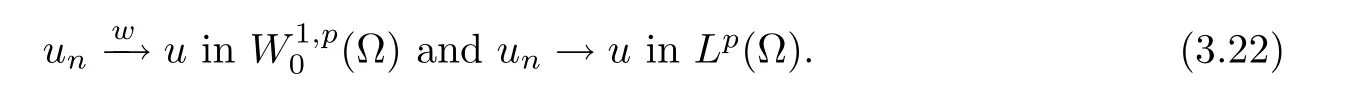
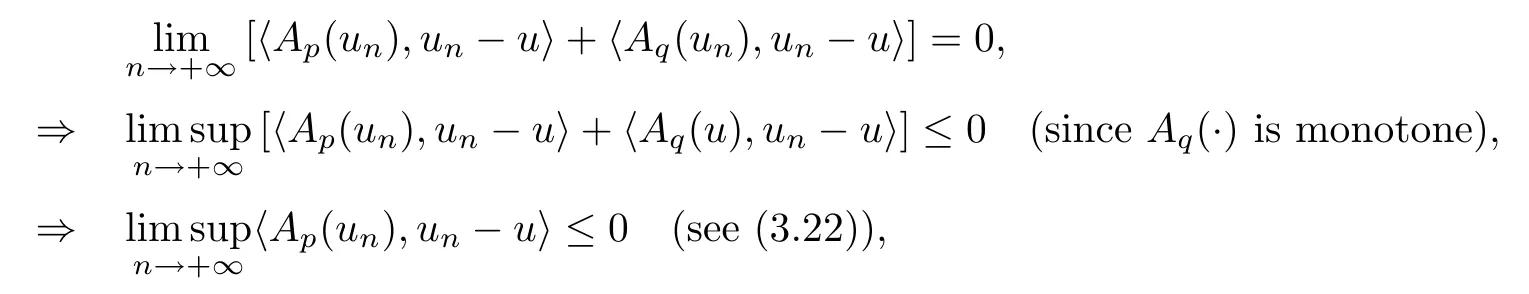
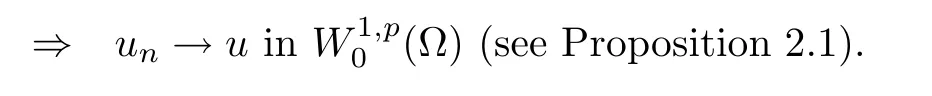




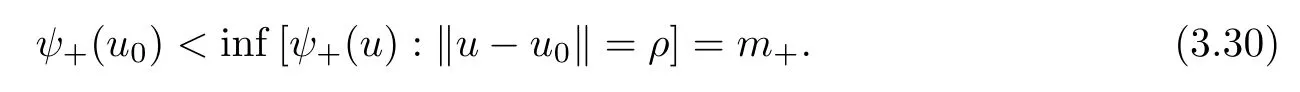

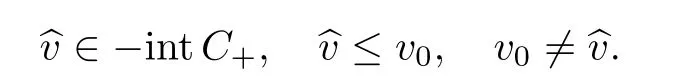
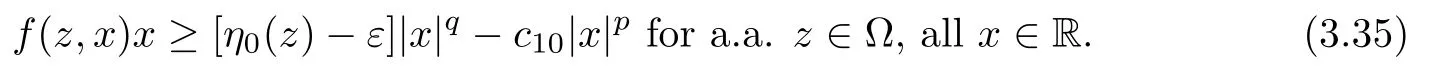
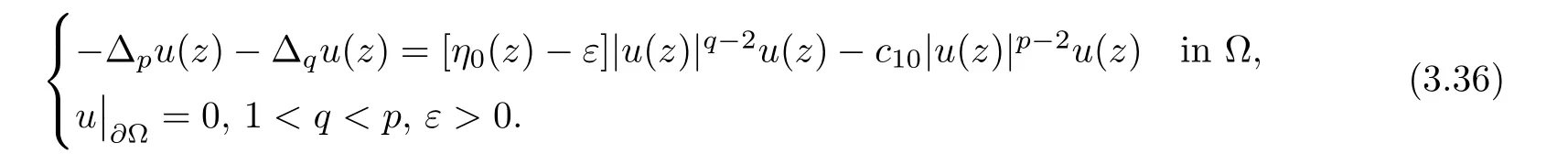
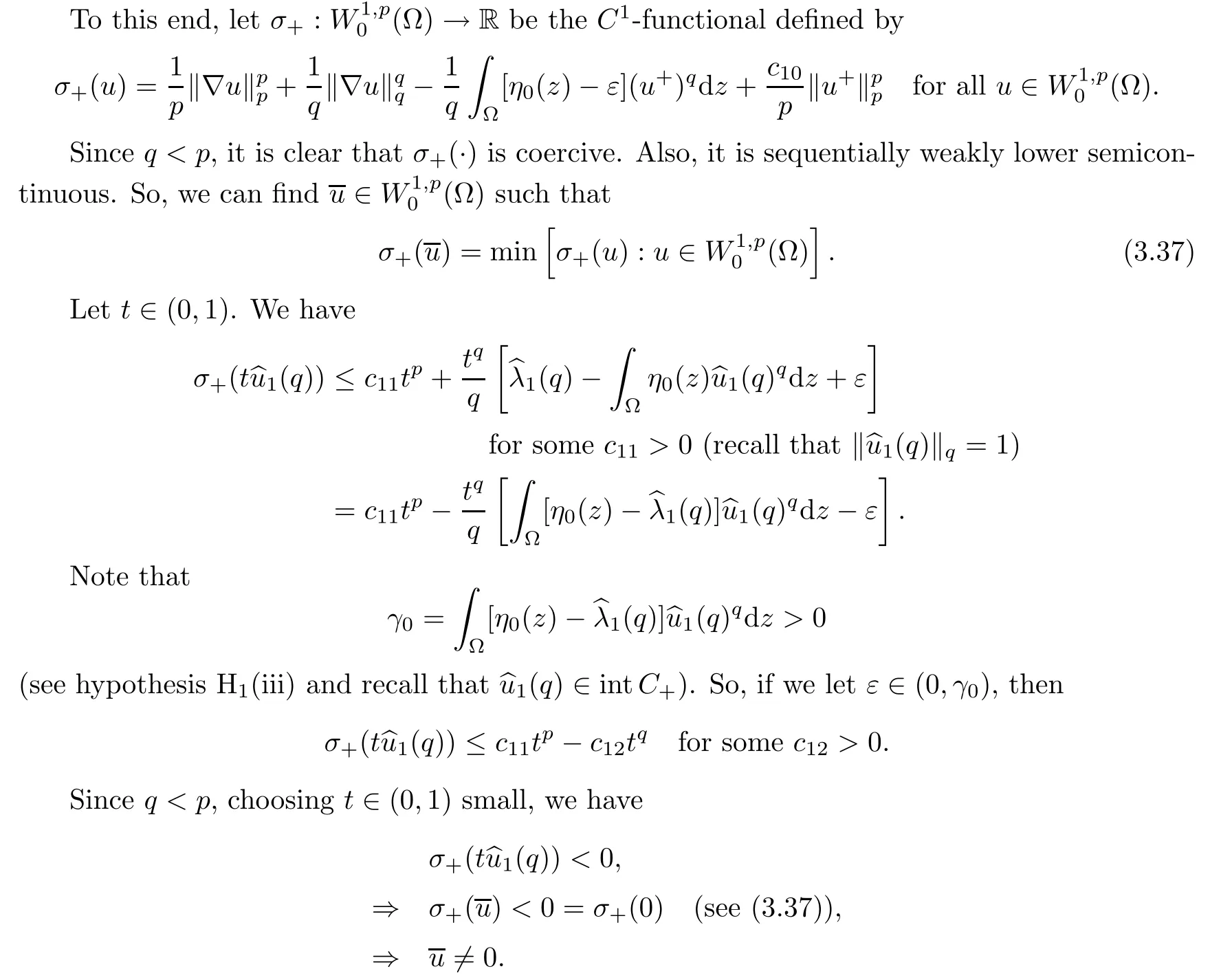

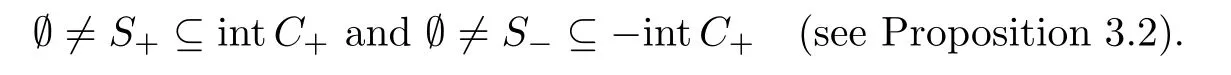

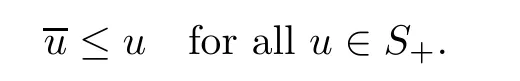

4 Nodal Solutions


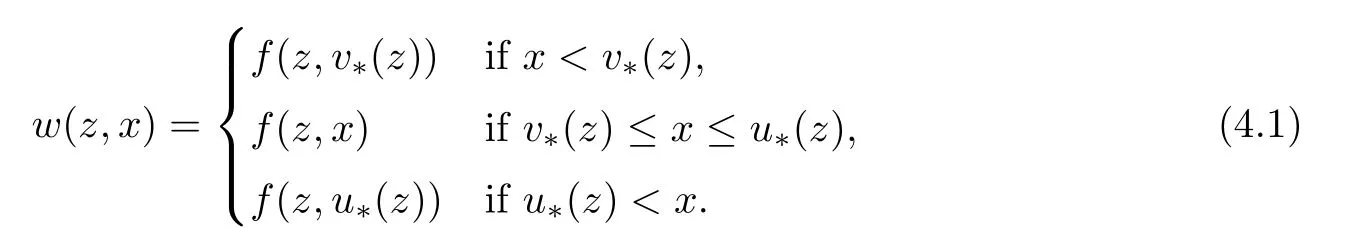


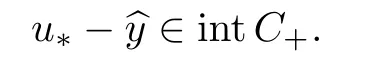


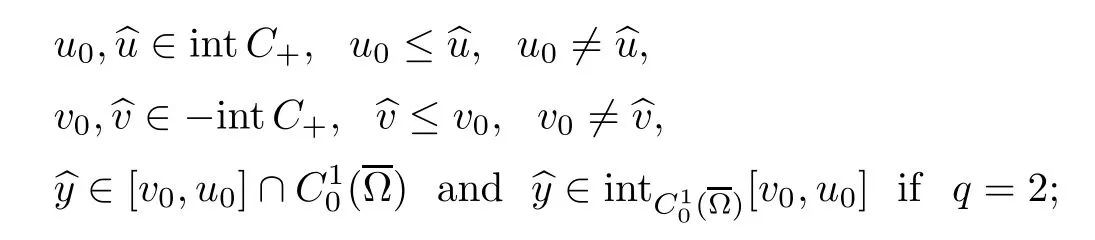
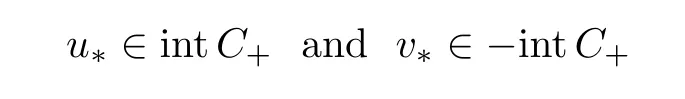
5 The(p,2)-Equation
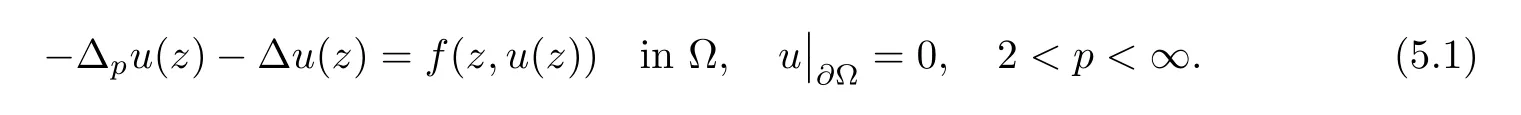
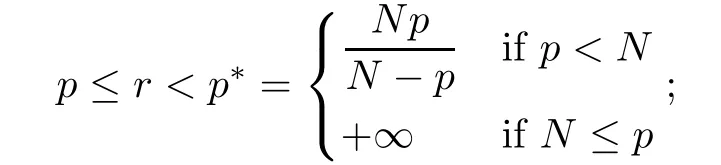
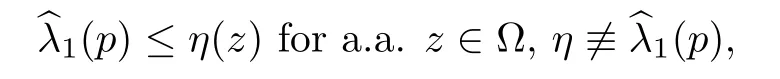
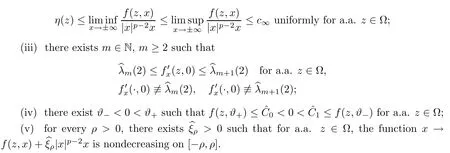


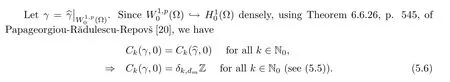
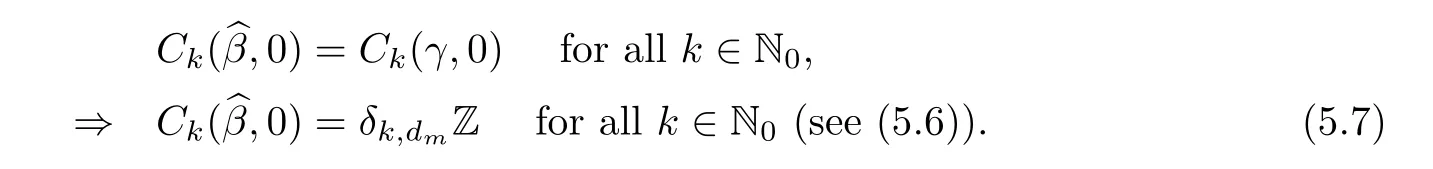

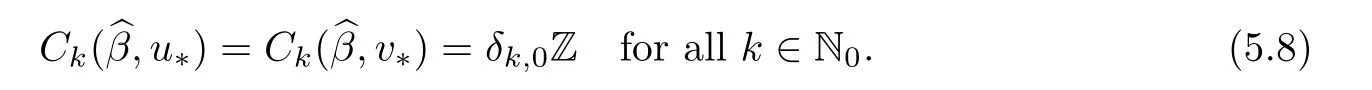

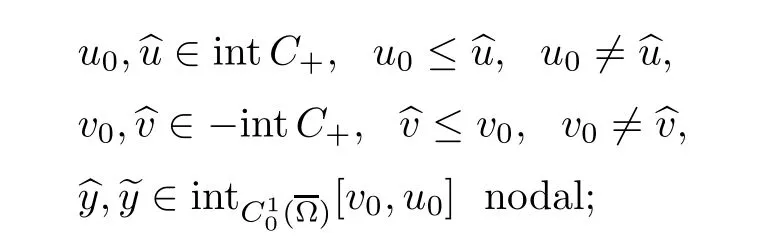
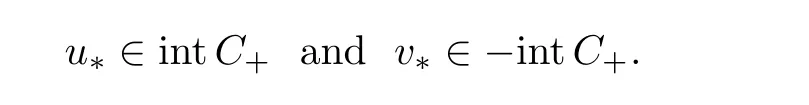
 Acta Mathematica Scientia(English Series)2021年5期
Acta Mathematica Scientia(English Series)2021年5期
