PDTR模型对城市流动人口的预测

吴 宇，孙宏宇，孙明辰，王洪君

(吉林师范大学 计算机学院，吉林 四平 136000)

0 引 言

人口迁移这一社会现象目前已经引起多学科交融研究领域学者的关注，从图1、图2可以看出，各个省份的净人口流动数量与自然增长率趋势截然不同。数据表明各地区的人口数量变化情况是受条件影响的，并不完全取决于人口基数，受人口迁移的影响也十分显著。进行人口迁徙预测可以更好的把握地区人口变化情况以及地区城市化情况，对社会经济发展具有重要指导意义。因此，进行人口迁徙预测研究势在必行。但目前研究上存在一些不足，一方面城市参数众多，应用现有技术将其统计可以轻易实现，但其中掺伴的无效数据，不仅无形中提高了实验的能耗，也造成了数据混淆；另一方面，传统的人口流动预测方法大多是根据经济、政策等理论来总结人口流动规律加以预测。如：流动人口的规模总量和结构形式随经济体发展变迁的规律、城市收入水平和公共服务能力差异，是吸引外来人口流入的首要因素等等[1]。但无论使用什么方法，其根本在于分析人口流动情况和其影响因素之间的关系，并通过该关系构建模型或形成理论预测未来人口变化情况。

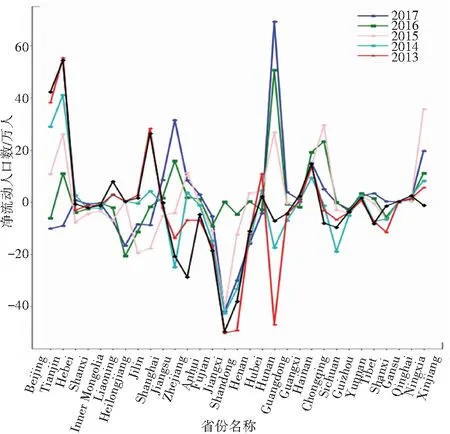
数据来源：国家统计局发布

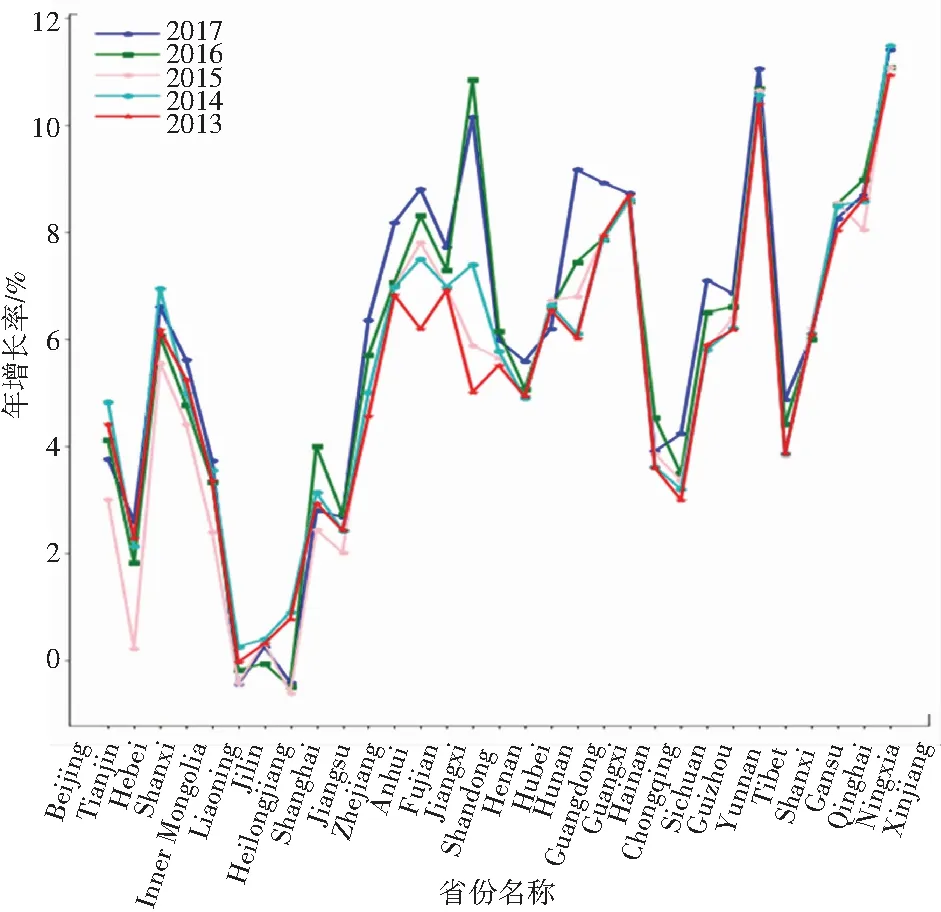
数据来源：国家统计局发布

随着科技的发展，通过人工智能的方法进行大数据分析预测城市人口，可以节省大量的时间以及资源的消耗。数据的获取以及预测算法的选择在很大程度上影响着预测结果的精确性，不同模型对于人口的预测结果也不同[2]。本文旨在提出一种PDTR预测模型，通过使用人工智能算法，总结出人口流动与影响其发生变化的城市参数之间的关系并形成模型，以进行对各省份未来人口流动情况的预测。

1 PCA原理

PCA方法可以利用降维思想抓住所要研究问题的主要矛盾，简化复杂问题，使研究效率得到提高[3]。

本文从燃气、供水、供热、公共交通、城市市容、绿地园林等7个方面中，选取46项城市参数指标，由于在选择训练样本时，各个样本指标之间的可能相关性较高, 所以可能导致样本信息过度重复的情况 , 这时就需要借助 PCA 方法来概括诸多信息的主要方面 ,对样本指标信息进行降维。通过这些综合指标相互独立地代表某一方面的性质 , 从而改进训练样本的有效性[4]。

将现有m个城市指标参数组成的原始数据集，分别用I1，I2，...，Im表示，由这m个城市参数指标组成了m维随机向量I=(I1，I2，...，Im)，设α为随机向量I均值；随机向量I线性变换成新的综合变量，用D表示。新综合变量D与原始变量I线性关系由公式(1)表示[5]：

(1)

式中：系数αij可以根据下面几个原则来确定：

(1)α112+α122+...+α1m2=1(i=1，2，…，m)；

(2)Di与Dj(i≠j;i,j=1，2，…，n)线性无关；

(3)D1为I1，I2，...，Im所有线性组合中方差最大者；D2为与D1不相关的I1，I2，...，Im的所有线性组合中方差最大者；Dn为D1，D2，...，Dn-1都不相关的线性组合中方差最大者。

这样确定的新变量指标D1，D2，...，Dn分别称为原变量指标I1，I2，...，Im的第1主成分，第2主成分，...，第n主成分。其中，D1，D2，...，Dn的方差依次减小。实际问题分析时，常挑选前面几个最大的主成分，这样既可以减少变量的数目，又抓住了问题的主要矛盾，简化了各变量之间的关系[6]。

本文最终使用PCA的fit方法，对全部训练数据进行训练，得到训练好的PCA模型。输入格式为fit(X)，其中X是预处理后的训练集数据样本。通过PCA的transform方法将全部训练数据进行变换，得到经过主成分分析后的特征。输入格式为transform(X)，其中X是待转换的数据，也是后续决策树分析的输入数据。

2 PDTR模型构建

决策树是一种树形结构的分类与回归方法[7]，其目的是通过对训练集进行学习，找出特征和类别之间的关系。一旦这种关系被找出，就能用其来预测未知类别数据的类别。本文使用决策树回归分析方法进行回归分析，所谓“决策”就是进行一次选择，每进行一次选择实质上就是对特征空间进行一次划分，每划分出一个单元该单元就会有一种特定的输出[8]。而划分或做“决策”的过程就是建立决策树的过程。本文使用标准差标准化和主成分分析(PCA)进行数据与处理，对预处理后的数据使用决策树回归模型(Decision Tree Regression)进行回归分析，以得到预测模型。具体流程如图3所示。

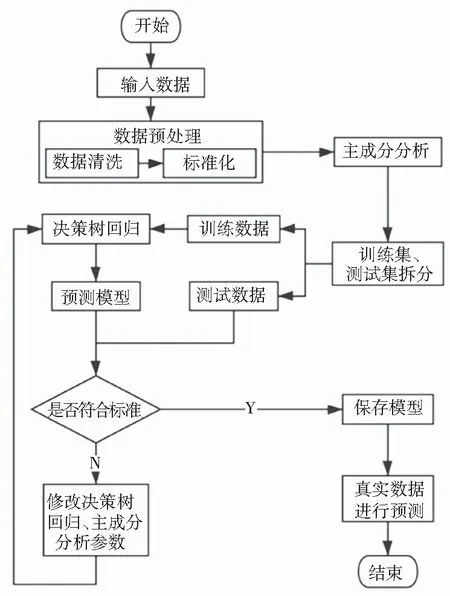
图3 PDTR模型的总体设计方案流程图

实现步骤如下：

(1)对输入数据进行预处理，其中包括数据清洗和标准化；

(2)对处理后的数据进行主成分分析，得到降维后数据；

(3)使用降维后数据训练决策树模型；

(4)对测试数据进行预测得到结果，若结果达到标准则保存模型对真实数据进行预测，否则修改主成分分析和决策树回归模型的参数，返回步骤(3)继续进行第三步操作。

3 实验与结果分析

3.1 数据集

本文实验数据来源于2006～2017年《中国统计年鉴》，从各年的数据中选取供热、供水、燃气、城市市容、公共交通、绿地园林等6大类城市参数指标，共45小项数据类别进行分析，将各年的出生率、死亡率、年增长率和6大类城市参数指标进行了集成用于预测实验。详细情况见表1。

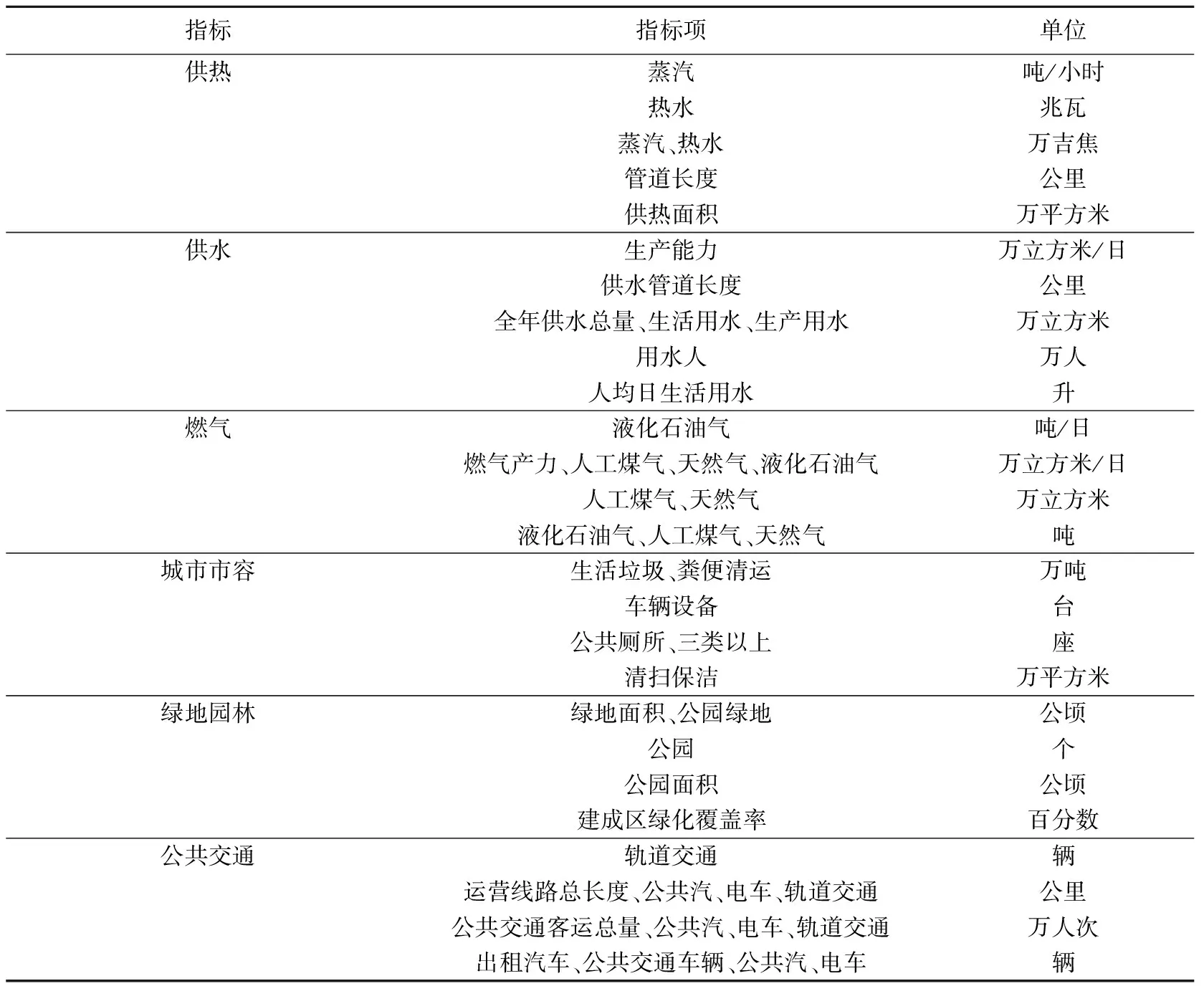
表1 城市参数数据集

3.2 实验及结果

数据的完整性很重要，会影响到后续的数据处理。本文对于重要的数据，使用的是相对于丢弃更常用的补全。首先利用Pandas的fillna方法，将原始数据集中的缺省值部分填充为相应特征下样本的平均值(df.fillna(df.mean()['chas':'rm']))；再利用StandardScaler对上一步处理后的数据，采用公式(2)进行数据去均值和方差，实现数据归一化，以便更好地对数据进行特征提取。

(2)

式中：μ为所有样本数据的均值，σ为所有样本数据的标准差。

将归一化后的6个指标(x=(x1,x2,...,x6))作为PDTR模型的自变量，将流动人口(10万人)y作为因变量。

本文共采集46项城市参数指标，为了更好的保存数据信息且提高实验效率，使用PCA时选取了前24项主成分，将数据从46维降维24维；在使用Decision Tree Regression时，本文针对2016年数据，将max_depth参数即决策回归树的最大深度设置为从1开始，通过不断迭代直至达到极限，得到图4所示结果。将min_weight_fraction_leaf参数，即最小权重系数设置为从0开始，通过不断迭代直至达到极限，得到图5所示结果。

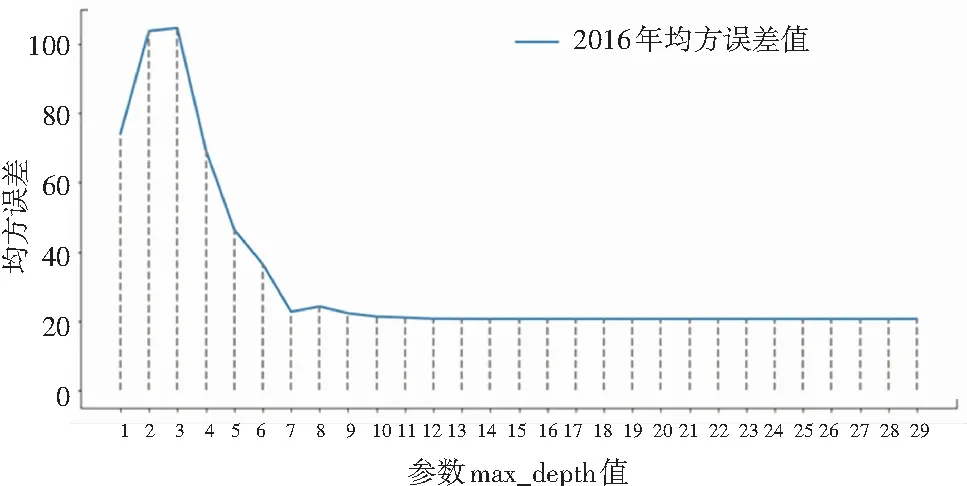
图4 2016年均方误差变化情况

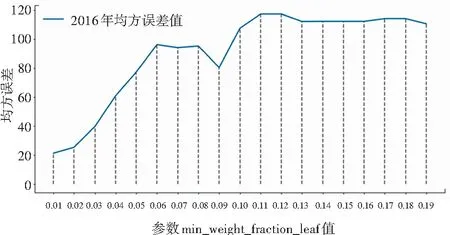
图5 2016年均方误差变化情况

图4中蓝色折线代表2016年份的原始数据经数据预处理后，对设置了不同max_deep值的决策树回归模型进行训练，得到的均方误差值。从图4中可以看出，将max_deep值设置为14时，预测的绝对误差相对较小。因此，本文在使用决策树回归模型时将该参数设置为14。

图5中蓝色的折线代表2016年份的原始数据经数据预处理后，使用处理后的数据对设置了不同min_weight_fraction_leaf值的决策树回归模型进行训练，得到的均方误差值。当min_weight_fraction_leaf值设置为0时，代表不使用权重。从图5中的趋势可以看出，当该参数值设置为0.01时，均方误差达到最小。因此，本文将该参数的值设置为0.01。

本文从研究总体中选择2013年的数据作为训练集，将2014～2017年的数据作为测试集。将预测值与真实值进行比较，并计算平均绝对误差(MAE)、均方误差(MSE)、中值绝对误差(MDAE)、可解释方差值(EVS)和R方值(R2)，与进行过数据标准化和PCA处理的SVR算法进行比较，实验结果见表2。

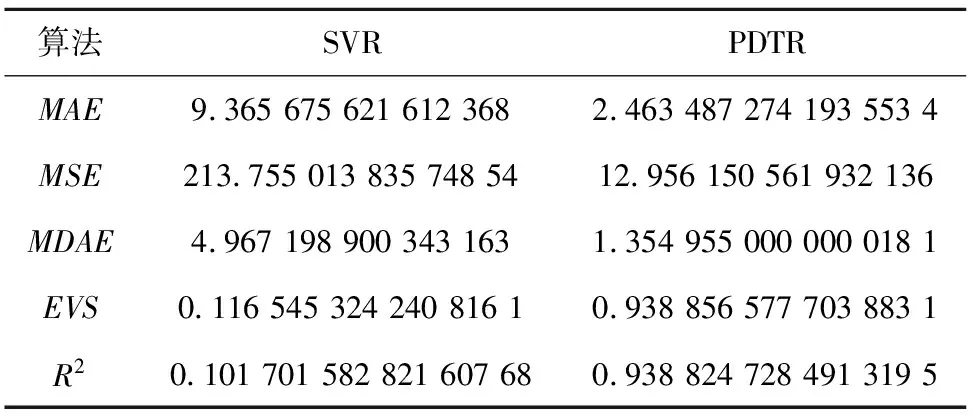
表2 模型评价

由于本文进行对比分析的数据样本数量相同，因此R2值可以很好地反映出本文所使用的回归模型拟合程度效果的好坏。从表2可以看出，本文提出的算法与SVR相比，平均绝对误差、均方误差、中值绝对误差的值更接近于0，可解释方差和R方值更接近于1，证明PDTR模型性能良好。从图6～图9可看出，模型对2014～2017这4年预测的结果变化趋势与真实值近乎相同。

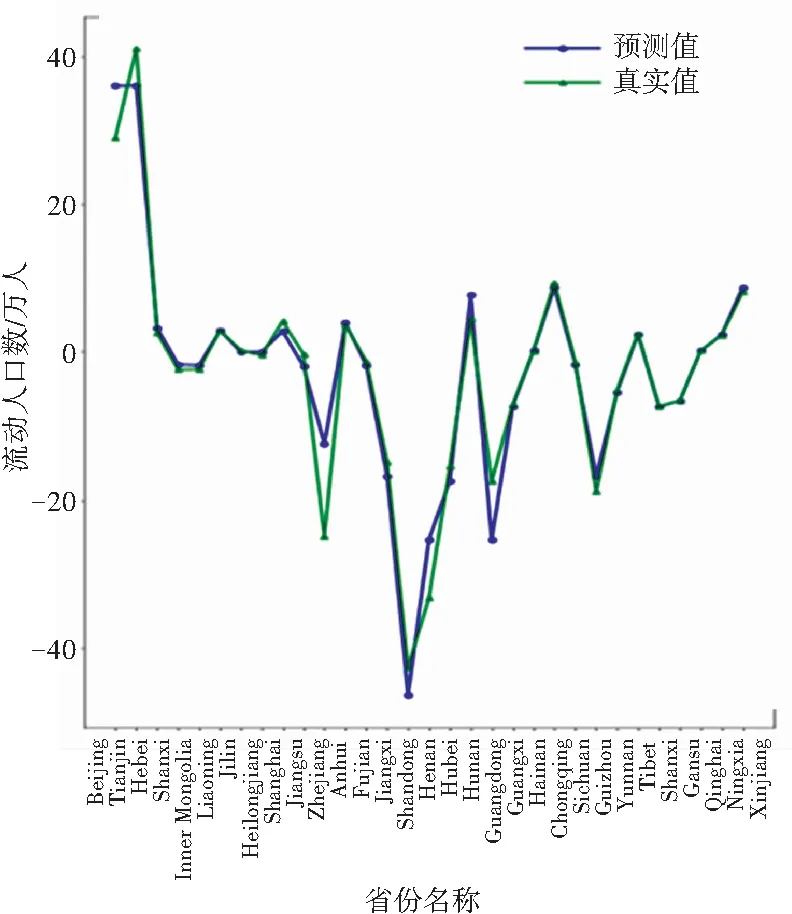
图6 2014年对比图

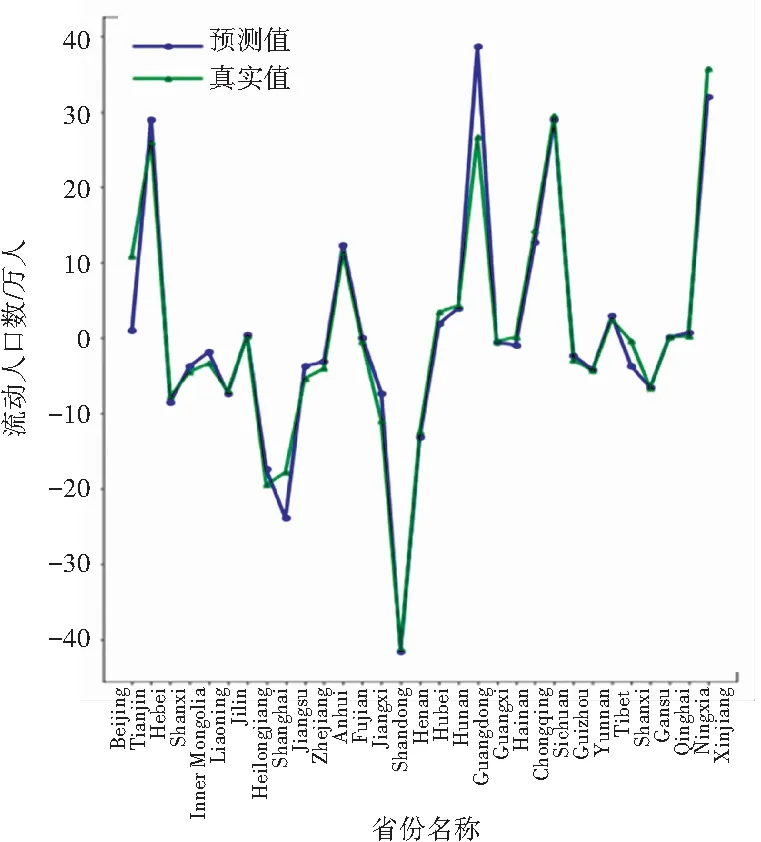
图7 2015年对比图

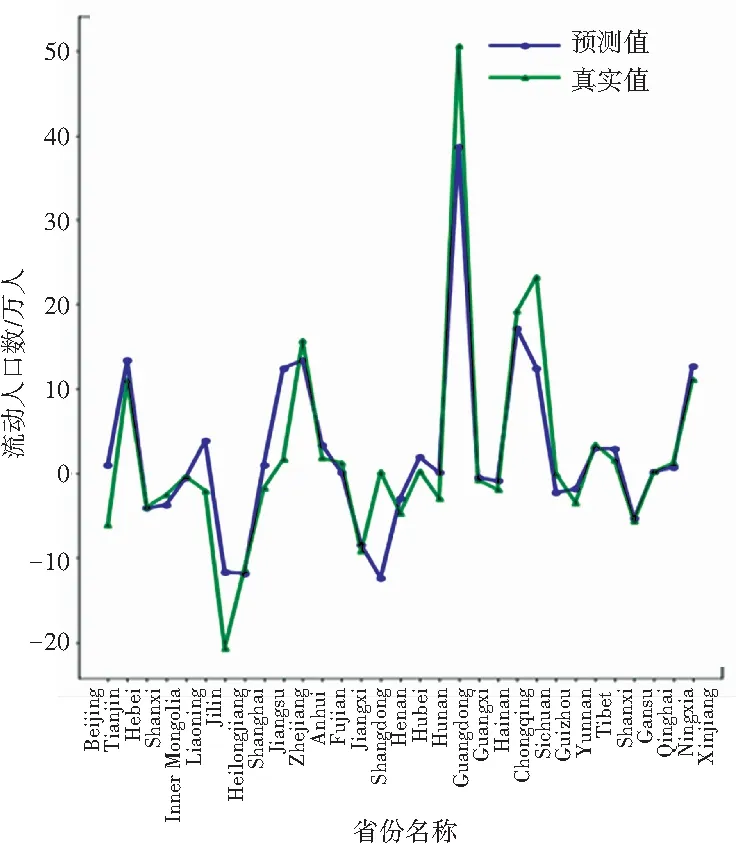
图8 2016年对比图

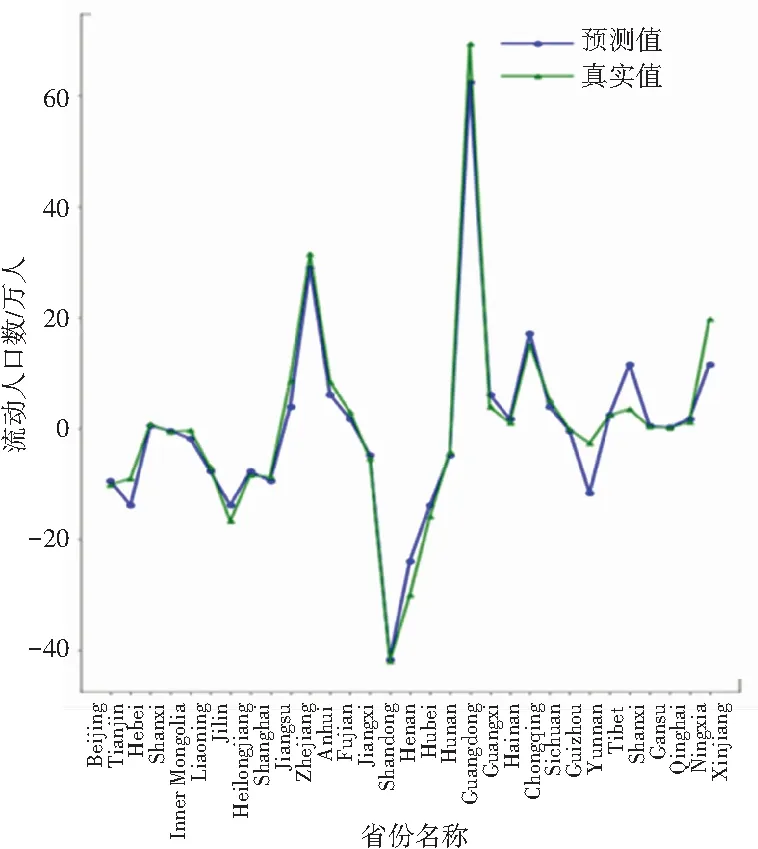
图9 2017年对比图

4 结束语

本文探究了国内各城市人口流动情况与城市参数之间的关系，选取了6种城市参数(燃气、供水、供热、城市市容、公共交通、绿地园林)共45项指标。由于不是所有指标都对人口流动有影响，因此对原始数据进行特征提取，选出有效特征进而进行数据分析。本文提出的PDTR模型通过实验分析，可以很好地解决上述问题。本文采用主成分分析方法(PCA)进行特征提取。该方法可以在很大程度不损失数据信息的条件下，对原始高维度数据进行降维，即通过变换映射到低维空间中。通过实验验证，PCA的n_components超参数为24，对原始数据进行去燥和降维；Decision Tree Regression的max_depth超参数为14、min_weight_fraction_leaf超参数为0.01时，可以很好的进行预测，得到的结果相对准确。