基于FAHP组合赋权TOPSIS的电能质量综合评估

刘康康，杨 超，薛仰孝

(1 贵州大学 电气工程学院，贵阳 550025; 2 国网渭南供电公司, 陕西 渭南 714000)

0 引 言

现代电力系统的快速发展，大量分布式电源接入和非线性负载大量使用，导致电网电能质量问题日益突出。另一方面，现代电力电子设备的应用和高精度仪器越来越多，使得大量的电力用户对所获得电能质量的要求变得越来越高，加剧了电力系统供需双方之间的矛盾[1]。因此，对电能质量有科学严谨的评估，反映电网电能质量的整体状况，这对全面考核电力市场环境下电网的电能质量、优质电能电价的制定和电能质量管控模型研究具有重大意义[2-3]。

国内外已有大量的学者就电能质量综合评价方法进行研究。如：将层次分析法(AHP)与模糊综合评价法相结合实现对电能质量评估，但只注重主要评价指标，使得评估过程中的主观因素过强，导致最终的评价结果不符合客观实际[4]；在模糊综合评价的基础上，引入对抗性的交叉数据包络分析(data envelopment analysis, DEA)模型[5]；CRITIC的电能质量评估方法，利用CRITIC确定客观权重，避免了主观加权带来的实际情况偏差，同时CRITIC方法充分利用了数据，并通过对比强度和冲突来描述数据指标与波动之间的关系，从而有效地利用了数据[6]；通过改进雷达图法实现对电能质量综合评估[7]；将物元理论与证据理论相结合，实现对电能质量的评估，降低不确定性因素在评估过程中的影响[8]。CRITIC-TOPSIS综合评价方法，利用CRUTIC赋权法解决各评价指标间存在的差异性和关联性，使赋权结果更加客观、切实，同时采用评估对象与理想解的相对距离替代传统理想解法(TOPSIS)的相对贴近度，增强TOPSIS 算法在实际运用过程中的广泛性[9]。

本文提出基于FAHP组合赋权-TOPSIS模型的电能质量综合评估方法。采用模糊层次分析法(FAHP)对指标的主观权重进行计算，利用熵权法确定指标的客观权重。为避免评估过程中单一赋权法的不足，对主客观权重进行组合，得到最终的评估权重向量，使评估结果更加客观可靠。在TOPSIS中利用一种基于夹角余弦的距离度量方式取代传统的欧式距离，以此改进TOPSIS模型在评价线性相关指标时存在的不足，使评价结果符合工程实际，并通过算例验证本文提出评估模型的可行性。

1 电能质量评价指标

电能质量是指供电企业对负荷侧的行业和居民的生产生活所供交流电的品质。理想情况下，供电公司应向负荷侧电力用户提供恒压、恒频的正弦交流电。发电机发电过程中存在三相不对称，分布式电源并网存在间隙性和不确定性；电网输电线路、变压器等设备在输电过程中出现电能损耗；用电负荷侧负载接入的随机性和复杂性，电力系统中控制技术和手段有限，导致在实际的供电系统中达不到理想状态。电源侧发出的电能经过电网的输配线路，到达负荷侧工业和生活用电可能达不到最低的标准，使得电力用户会遭受设备损坏、影响生产和生活。因此，对电能质量进行准确的评估具有重要意义。本文选取三相电压不平衡度Xεu、电压总谐波畸变率XTHDu、电压偏差的绝对值Xeu、短时电压闪变XPst、频率偏差的绝对值Xf、电压波动Xdu作为评估指标，构建如图 1 所示的指标体系。

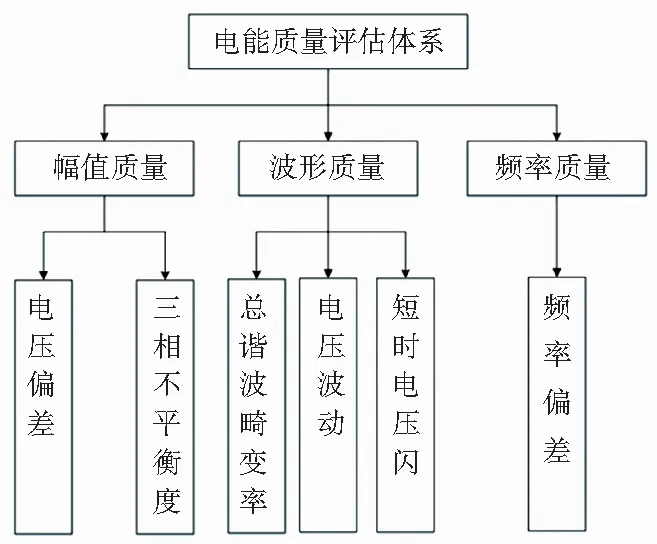
图1 电能质量评估指标体系

根据国家制定的标准，将上述电能质量评估指标大致分为5个等级，分别为优秀Ⅰ、良好Ⅱ、中等Ⅲ、合格Ⅳ、不合格Ⅴ5类。不同指标各等级取值范围见表1。

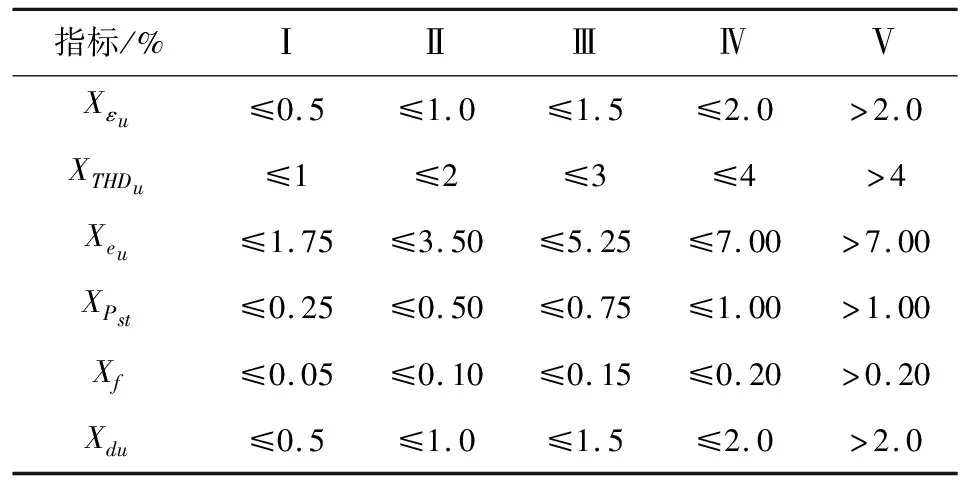
表1 指标等级边界值

2 电能质量FAHP组合赋权的TOPSIS综合评价法

2.1 模糊层次分析法(FAHP)

采用模糊层次分析法可以将专家的打分模糊化，降低其中的主观性影响。根据专家的行业经验，对各评估指标两两比较得到相应的评价矩阵。衡量两者间的重要性的方法采用(0.1～0.9)标度法，含义见表2。

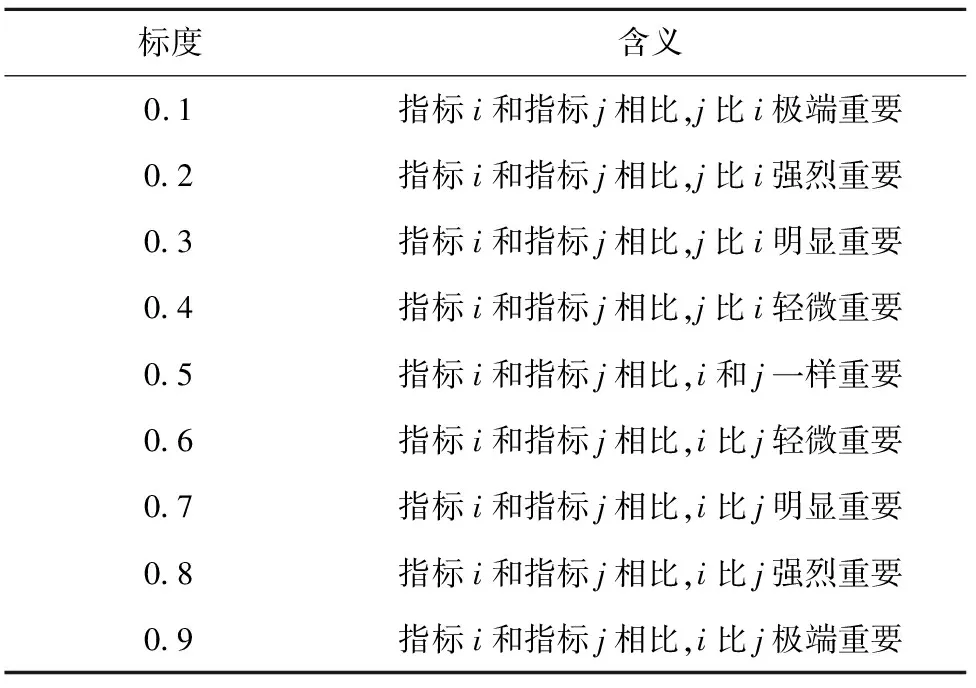
表2 (0.1～0.9)标度法含义

对于矩阵Rij(n×n)：

(1)若0≤rij≤1，则R是一个模糊矩阵；

(2)若rij+rji=1，则R是一个模糊互反矩阵；

(3)若∀i,j,k∈n,rij=rik-rjk+0.5则R为模糊一致矩阵。

对于模糊一致矩阵Rij(n×n)有式(1)：

(1)

主观权重的确定：

(1)对于电能质量，模糊互反矩阵Rl由S位专家评估组成，式(2)；

Rl=(rij(l))n×n,l=1，…，n

(2)

(2)模糊互反矩阵Rij(n×n)的聚合，式(3)：

(3)

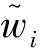
(4)

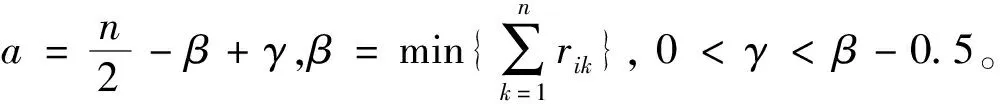
2.2 组合赋权

熵权法在决策过程中可对原始数据进行充分利用，用于客观赋权[10]，利用各指标的熵值包含信息量多少来确定评估体系中各个指标的客观权重。该法能够充分挖掘实际数据的信息，减弱人为因素的干扰，使评估结果契合实际情况。为发挥主客观权重信息在决策过程中的作用，将均衡反映主客观属性的组合权重作为指标的最终权重。设模糊层次分析法得到主观权重为w1，熵权法确定客观权重为w2，则组合权重向量为w=[w1,w2,…,wn]，即式(5)。

(5)

2.3 TOPSIS评估方法

TOPSIS是一种通过计算各评价对象的指标数据与理想指标数据的欧式距离对评价对象进行优劣排序的综合评价方法[11]。评价指标间通常存在一定的线性关联，TOPSIS法采用欧式距离度量各个评价方案与理想方案间的距离，这会使欧氏距离产生不可信问题。本文采用余弦相似性解决评价指标之间存在线性相关的问题，余弦相似性是基于夹角余弦的距离度量方式计算评价方案与理想方案的距离[12]。两个向量夹角越小，则相似性就越大，意味着两个向量之间的距离更短，反之亦然。

其基本步骤如下：

(1)设评估对象为m，评估指标为n，d为电能质量等级量。将评估数据和标准数据组合，得到样本矩阵X，即X=(xij)(m+d)n。在矩阵X中，第1行到d行是电能质量指标的等级样本，第d+1行到d+m行是评估对象测量样本。

由于评价指标的量纲不同，需对样本矩阵规范化，规范化的样本矩阵用Z表示，针对正向指标和逆向指标采用不同的无量纲化方法，式(6)和式(7)：

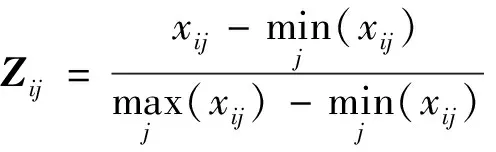
(6)

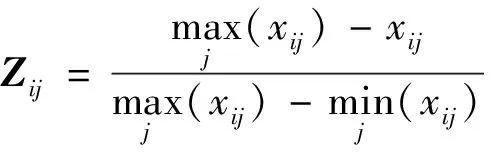
(7)

(2)建立加权样本矩阵Y=(yij)(m+d)n，式(8)；

yij=vj*zij

(8)

其中，vj是组合权重。

(3)确定正理想解A+和负理想解A-, 利用夹角余弦分别求解第j个待评价方案到理想解的距离，式(9)和式(10)。

(9)

(10)

其中，i=1, 2, 3,…,m，xc=0.5(Aj++Aj-)。

(4)计算各待评价对象的相对接近度Ci，式(11)：

(11)

根据与理想解决方案的接近程度对各种样本进行分类，Ci值越大越好，越小越差。

综上，基于FAHP组合赋权的TOPSIS模型的电能质量综合评估流程如图2所示。

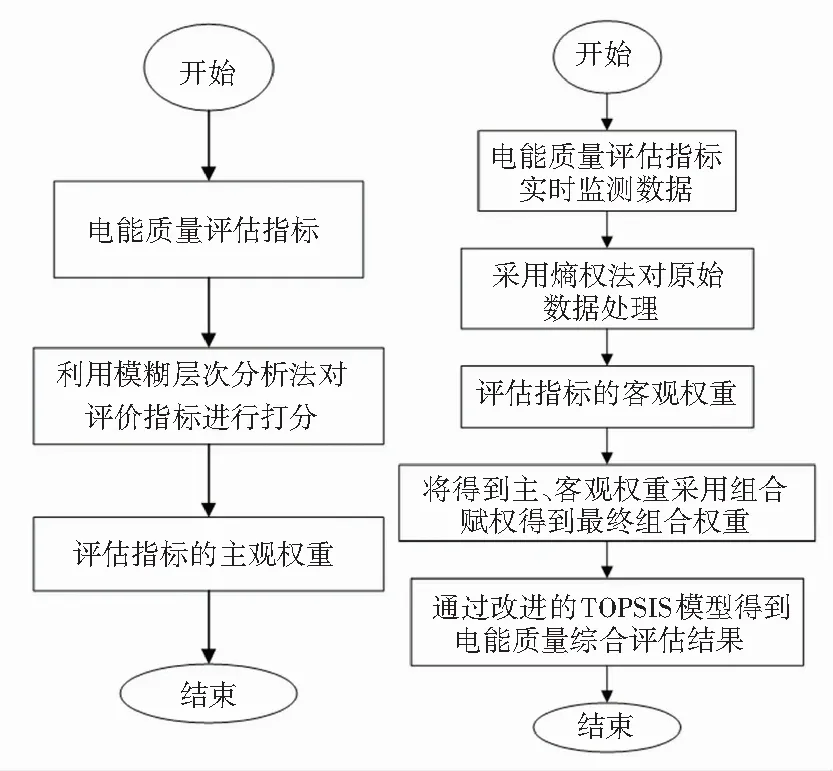
(a)主观权重 (b)综合评估

3 算例分析

本文利用河北某钢铁公司的两条10 kV 配电系统中主要的5个变电站母线的监测数据为电能质量实测数据，见表3[13]。进行实例分析，得出 FAHP-TOPSIS 法下电能质量综合评价结果。

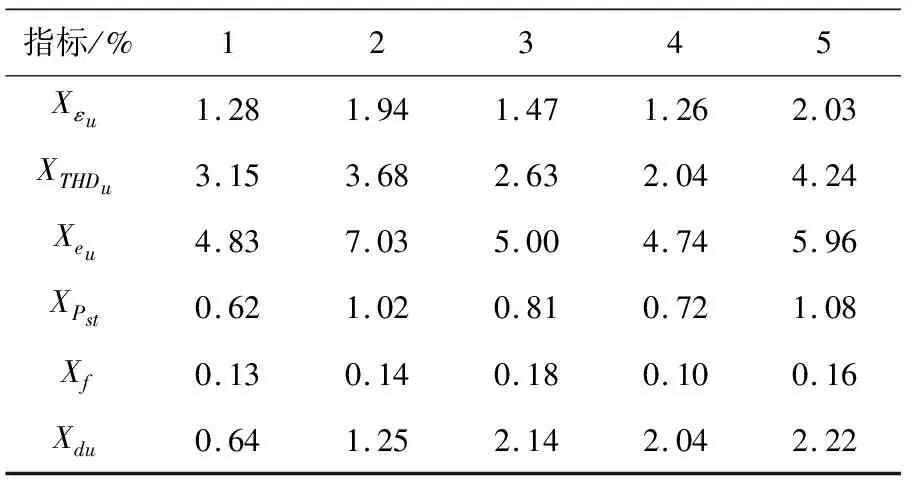
表3 实测数据

本文邀请5位有关专家针对电能质量的各个评价指标，根据9级标度法对评估指标作两两比较，得到相应的模糊评价矩阵，根据公式(1)～(3)得到由5位专家评估矩阵聚合的矩阵R。

本文取β=2.59，ξ=1.78，a=2.19，根据公式(4)得评价指标的主观权重向量w1为：

w1=[0.135 1 0.180 4 0.140 8 0.159 4 0.211 2 0.173 1]

根据监测点的实际数据，利用熵权法得出各个评估指标的客观权重向量w2为：

w2=[0.167 9 0.247 3 0.098 3 0.172 0 0.150 8 0.163 6]

由式(5)得到各个评估指标的组合权重向量w为：

w=[0.134 4 0.264 4 0.082 0 0.162 5 0.188 8 0.167 8]

将电能质量的等级范围值与实测数据组成电能质量样本综合矩阵X。

用式(6)、式(7)对上诉综合评价矩阵进行数据预处理，由式(8)得到样本加权矩阵为：

计算结果见表4，依据上述加权规范矩阵，根据式(9)～(11)可以求出各监测点的评价指标与正、负理想解的距离及贴近度。

与表2实测数据对比分析，监测点4的短时电压闪变、电压波动的绝对值均比监测点1的数值大，但是文中的评估指标为反向指标，结合各指标最终的综合权重，监测点 4 应比监测点 1更优。由表4可以得到5个监测点最终电能质量的综合评估结果，其电能质量优劣的综合排序为：点4，点1，点3，点2，点5。采用集对分析与可变模糊集对电能质量进行评估，对于5个监测点的电能质量优劣综合排为：点4，点1，点3，点2，点5[13]。可见，本文与采用集对分析与可变模糊集方法对于相同5个监测点的电能质量进行综合评估，得到的排序结果一致，因此本文提出的方法具有可行性。

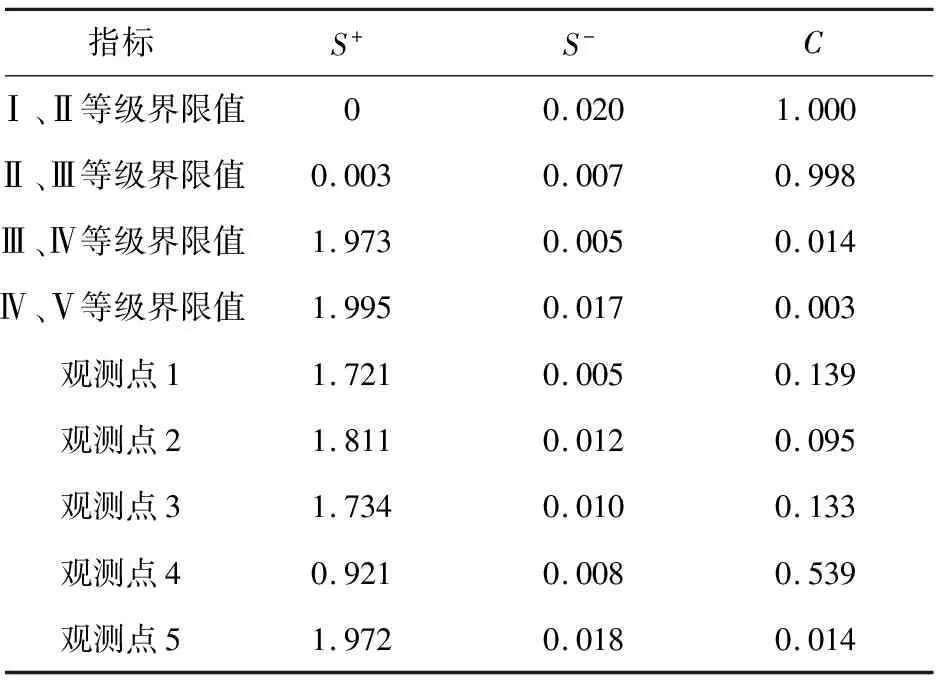
表4 计算结果

本文采用FAHP组合赋权的TOPSIS模型的电能质量综合评估方法，均衡考虑主客观权重信息在综合评估中的作用，用改进的TOPSIS模型消除评估指标间不同量纲指标间的关联性，使得结果更加可靠，增强了工程运用的广泛性。

4 结束语

本文从主观权重和客观权重两个方面对评估体系中各个电能质量评价指标的权重进行分析。主观权重是根据5位有关专家的行业经验采用模糊层次分析法确定，而客观权重则是用熵权法处理实测数据获得。为防止评估过程中采用单一赋权方法出现的不足，对二者进行组合得到合理的最终组合权重；在 TOPSIS 综合评价法中采用欧式距离，在处理线性相关指标时，相对贴近度存在瑕疵，使用余弦相似性解决线性相关问题，增强了TOPSIS 综合评价算法面对指标存在线性相关的适用性，因此本文提出一种基于FAHP组合赋权TOPSIS电能质量综合评价法，算例结果说明该方法的客观正确性和实用性，是一种可行的电能质量综合评估方法。