一类脉冲非线性分数阶微分耦合系统Cauchy问题的Ulam-Hyers稳定性

王 悦，赵凯宏

(昆明理工大学 理学院，云南 昆明 650500)

0 引 言

Ulam-Hyers稳定性问题可以追溯到文献[1]作者在1940年对扰动系统和原系统的逼近问题所作的重要研究.Ulam-Hyers稳定性的严格数学定义可参阅相关专著[2-3].Ulam-Hyers稳定性理论是完全不同于Lyapunov-type、Lagrange-type、Poisson-type、Popov-type等的稳定性.Ulam-Hyers稳定性问题已经吸引了许多学者的关注和研究.1993年，Obloza首先研究微分方程的Ulam稳定性问题[4].此后，许多学者也开始研究微分方程的Ulam-Hyers稳定性问题，并取得了大量丰硕的成果[5-12].

作为整数阶微分系统的拓展和延伸，特别在描述具有记忆和遗传特性的现象和过程方面，分数阶微分系统有着整数阶微分系统不可替代的优势.因此，分数阶微分系统的动力学行为吸引了许多学者的广泛关注和深入研究.特别是关于分数阶微分系统的Ulam-Hyers稳定性和广义Ulam-Hyers稳定性研究已经获得许多成果[13-16].文献[17]研究了如下的关于线性分数阶微分方程：

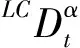
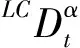
(1)

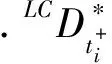
1 预备工作

首先给出分数阶积分的定义和相关性质，同时也对Mittag-Leffler 函数和拉普拉斯变换的定义和性质予以介绍.

定义1[28]连续函数f：[0，∞)→R的α>0阶Liouville-Caputo分数阶积分定义为：

定义2[28]如果f∈Cn([0，∞),R)且α>0，α阶Liouville-Caputo分数阶微分定义为:

实变量t∈(0,∞)的函数f(t)的拉普拉斯变换定义为:

(2)

引理1[28]对于任意的T>0，n-1<γ≤n，u(t)∈ACm[0，T] ，如果存在M>0，v>0，使得:

|u(t)|≤Mevt,t>T

成立，那么有:

(3)

定义3[28]经典的单参数Mittag-Leffler 函数Eα(z)和双参数Mittag-Leffler 函数Eα,β(z)定义如下：

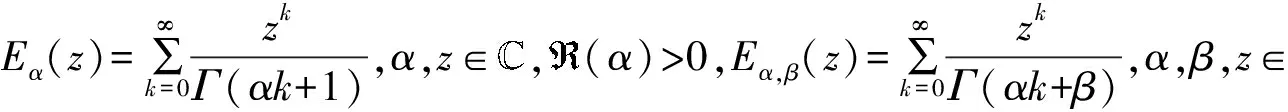
Mittag-Leffler函数的拉普拉斯变换为：

(4)

(5)

如果t∈0},α,β，λ∈，(α)>0，那么Eα(λtα)和tβ-1Eα,β(λtα)的整数阶导数为:

(6)

则线性分数阶微分耦合系统(6)的解为:

(7)

证明在系统(6)的两边运用拉普拉斯变换，并结合(3)可得:

整理上式可得

(8)

在公式(8)两边使用拉普拉斯逆变换，结合式(2)、式(4)及式(5)，可得:

和

这样就得到式(7).

(9)

其中：i=1,2,…，m,j=0,1,2,…，m.

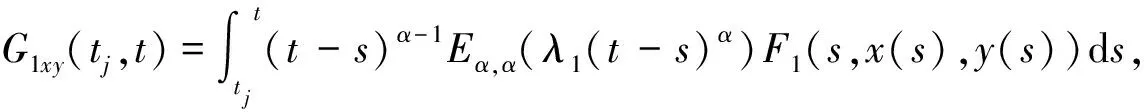
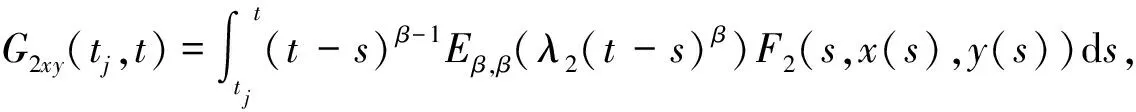
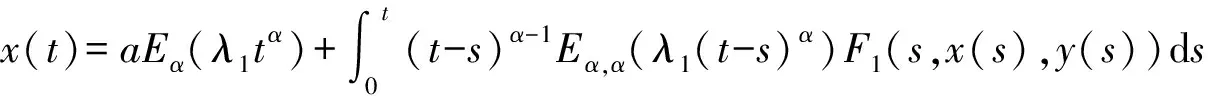
(10)

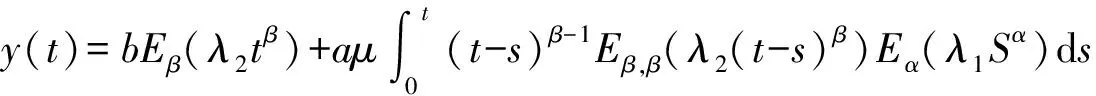
(11)

=bEβ(λ2tβ)+aμH(t0,t)+μH1xy(t0,t)+G2xy(t0,t)

根据式(10)、式(11)和系统(1)的脉冲条件，可得

(12)

(13)

(14)

当t∈(t1，t2] ，由引理2, 系统(1), 式(12)～式(14)可得：

(15)

(16)

根据系统(1)的脉冲条件、式(15)和式(16)，有：

(17)

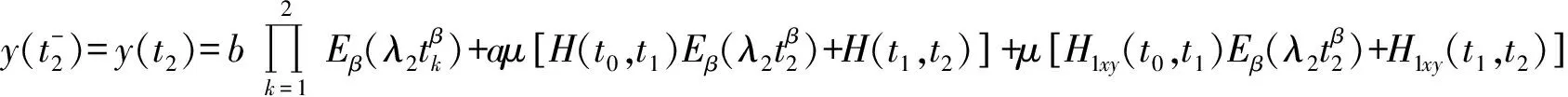
(18)

(19)

重复上面的过程，当t∈(ti,ti+1]，i=2,3,…,m,有：

(20)

(21)

2 主要结果

首先介绍Ulam-Hyers 稳定性的概念和一些基本引理.然后再证明本文的主要结果.

引理4[26]对于任意的λ≤0,α>0和t∈J，则有：

由于Beta函数B(·，·)在后面的推导中被多次用到，现介绍如下：

(22)

(23)

其中：λ1<0,λ2<0,i=0,1,…,m.

其中：λ1<0,λ2<0,i=0,1,…,m.

(24)

其中：i=1,2,…，m,j=0,1,2,…，m

(25)

(26)

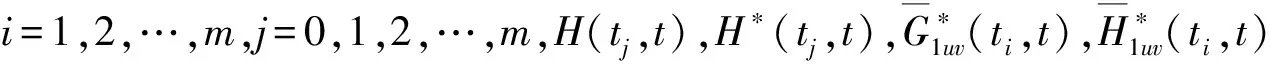
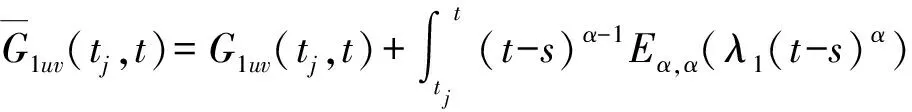
由式(22)和引理4，可得:

(27)

(28)

(29)

由式(26)～式(29)和引理4得:

(30)

(31)

(32)

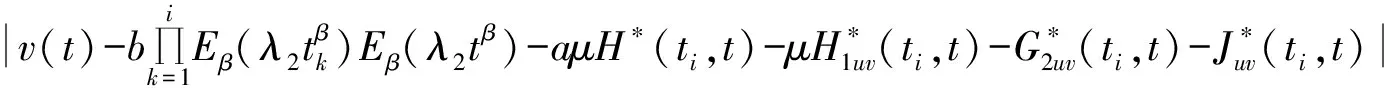
(33)

接下来研究系统(1)解的存在唯一性和Ulam-Hyers稳定性.为此先介绍如下一些假设条件：

(C1)0<α,β<1,λ1<0,λ2<0,μ,a和b都是实数；

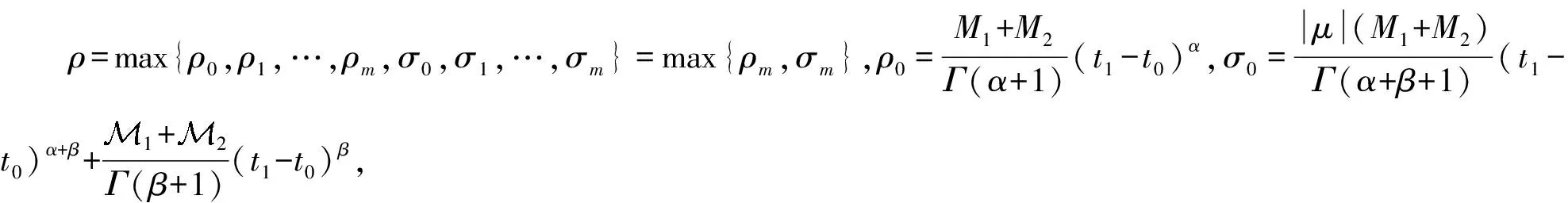
定理1假设条件(C1)～(C4)满足，那么有以下结论成立：

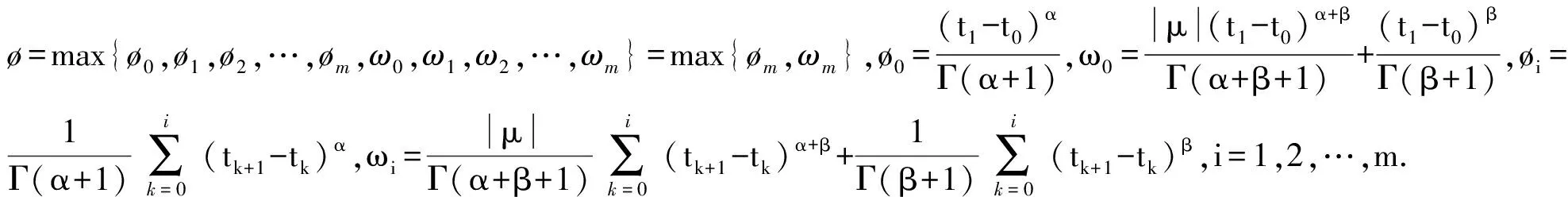
(T(x,y))(t)=((T1(x,y))(t),(T2(x,y))(t))

(34)

(35)

(36)

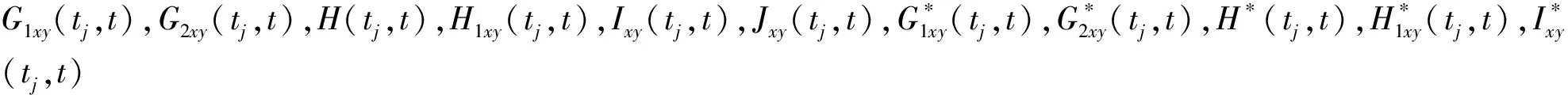
首先，应用Banach压缩映射原理去证明定理1的结论(i)成立，可分两步进行.

这表明(T1(x,y))(t),(T2(x,y))(t)∈AC1[J].根据条件(C1)～(C3)，对于i=1,2,…,m，j=0,1,2,…,m，有：

(37)

(38)

(39)

(40)

(41)

(42)

(43)

(44)

(45)

由式(37)～式(45)，可得：

(46)

(47)

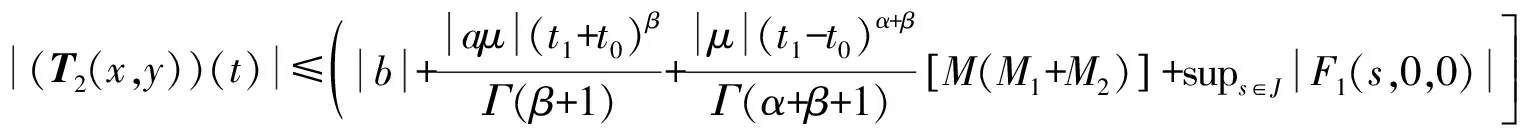
(48)

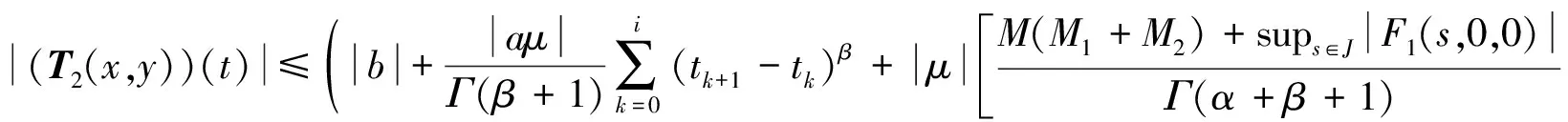
(49)

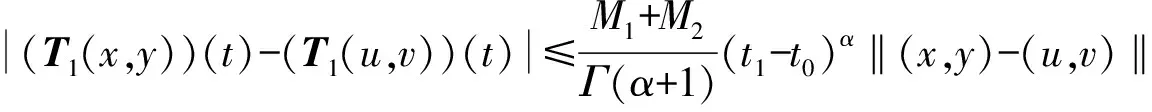
(50)

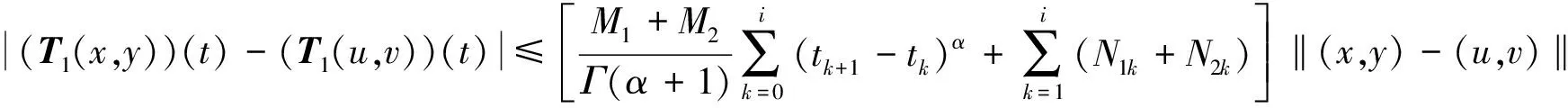
(51)

(52)

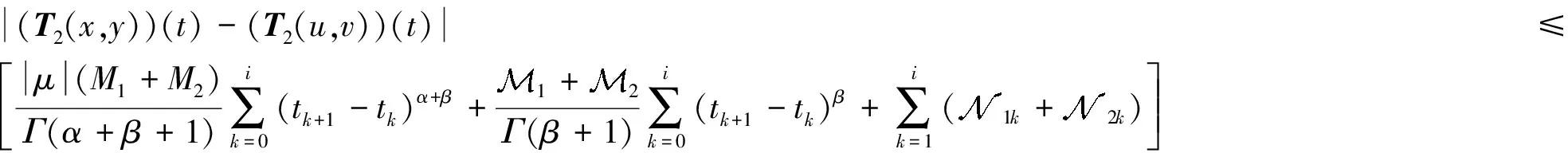
由式(50)～式(53)可得:

(54)

(55)

3 举 例

考虑下面的脉冲非线性分数阶微分耦合系统的Cauchy问题：

(56)

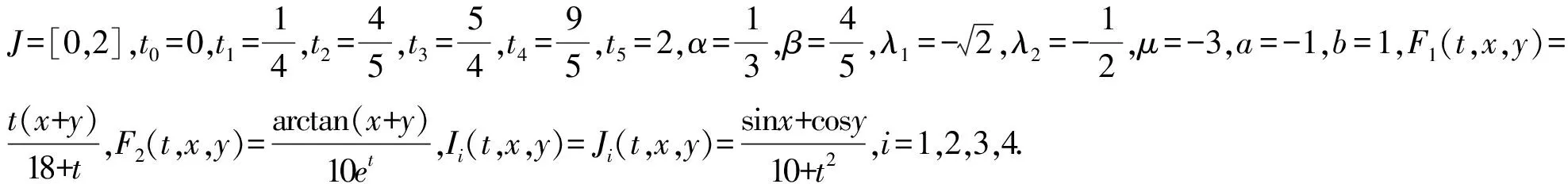
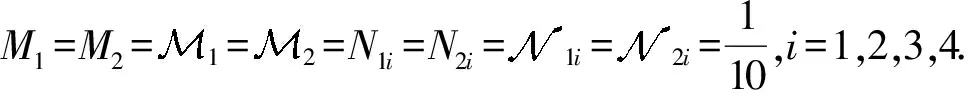
于是定理1中的(C1)～(C3)条件满足.现在需要验证条件(C4)成立.事实上，由于ρ0<ρ1<ρ2<ρ3<ρ4,σ0<σ1<σ2<σ3<σ4,ø0<ø1<ø2<ø3<ø4,ω0<ω1<ω2<ω3<ω4, 因此只需计算ρ4,σ4,ø4,ω4, 即：

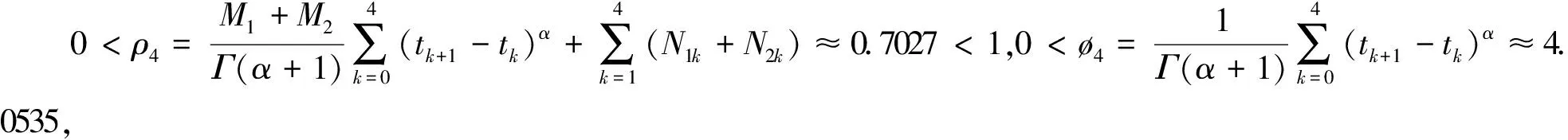
4 结 论

脉冲分数阶微分方程在刻画瞬时变化的现象和过程方面具有很大的优势.据我们所知，脉冲非线性分数阶微分耦合系统Ulam-Hyers稳定性的研究结果是比较少见的.因此，对系统(1)的研究既新颖又富有挑战性.在研究过程中主要运用拉普拉斯变换，Mittag-Leffler 函数，不动点定理，不等式技巧等数学方法.这些技巧和方法对于研究类似的数学问题也是行之有效的.从ρ和ø的表达式可见耦合系统的两个状态变量对系统解的存在性和Ulam-Hyers稳定性是相互影响的.