基于利率期限结构对我国债券投资组合管理策略的研究

摘要:随着市场化利率的深入改革,我国债券投资组合面临波动的市场利率要更加警觉,因此提前了解利率期限结构的变动对债券投资组合的影响很有必要。本文采用2020年5月8日在上海债券交易所上市的国债数据推导出利率期限结构,通过利率期限结构结合收益率曲线策略来建立优化的组合管理应对利率的波动。
关键词:利率期限结构;收益率曲线策略;债券投资组合
引言
长期以来,利率风险都是我国债券投资组合面临的一种主要风险,对于波动的利率产生的风险进行防控,很多研究者通常采用利率免疫策略来规避投资组合中面临的利率风险(信怀义等,2017),结果表明三因子利率动态模型在面对利率大幅波动性风险时免疫效果要优于持续期对冲法和久期凸性对冲法。彭安兴等(2017)研究发现债券的投资收益会随着持有期限越长收益越稳定。还有投资者从组合债券的投资决策进行分析,取得预期收益的情况下把风险控制在合理范围内(孙明等,2019)。也有研究者从投资者角度,测算高收益债券的投资收益,研究高收益债券的配置策略(刘代民,2020)。本文研究通过利率期限结构构造不同期限的债券组合来应对利率的波动,使债券组合可以在低风险下获得较高的收益。
二、相关理论基础
(一)利率期限结构理论
利率期限结构是指在某一个时点有相同的风险、流动性和税收待遇等,而期限不同的零息票债券的到期收益率组成的一条曲线,也即是零息票债券的收益率曲线。即期利率的公式表示为,其中Pt为零息票债券的价格,Mt为零息票债券到期日的价格,st为即期利率。
(二)债券投资组合管理策略
债券投资组合的管理策略根据投资者认为市场是否有效,大体上可以分为两种:一种是肯定市场的有效性,债券投资组合不追求市场的超额收益,而是获得对应所承担风险应获得的收益,这就是消极的投资组合策略。另一种是不认为市场是有效的,投资者认为只要能把握住机会是可以战胜市场的,试图找出被市场错误定价的债券和预测利率的波动进行套利,调整组合头寸后获得超额收益,这就是积极的债券投资组合。
收益率曲线策略就是积极的债券投资组合中的一种,根据债券的利率期限结构,针对债券投资组合采用预期未来收益率形状的变动来建立优化的组合管理,用不同的投资组合管理办法来应对不同的利率波动。
通常采用的收益率曲线策略有子弹式策略—在某一期限范围内进行准确投资,期限范围中期一般是集中在该范围内。哑铃式策略—期限两端的范围是该策略投资集中范围。梯子式策略—不同期限等权重的头寸是该策略的选取范围。
我们将短期债的剩余期限范围锁定在0-3年,中期债券的剩余期限范围锁定在5-10年,长期债券的剩余期限范围锁定在10年以上。
子弹式策略选取δ=7,Δδ=0.5,(δ表示债券的剩余期限)当债券的剩余期限落入(δ-Δδ,δ+Δδ)内,则买入,当债券的剩余期限落入此范围外的则卖出,此时投资组合的头寸主要集中在(δ-Δδ,δ+Δδ)内。
哑铃式策略选取δ1=3,δ2=10,当债券的剩余期限δ0落入(0,δ1)∪(δ2,∞)内,买入债券,当债券在此范围外时则卖出债券。此时,投资组合的头寸主要集中在短期债券和长期债券。
梯子式策略选取各期限债券在组合中的权重是相等的,即组合中的债券在短期,中期和长期债券中所占比重是同等的。
下面我们以子弹式策略为例:
首先,我们选出剩余期限在(6.5,7.5)年之间的债券,根据利率期限结构,将即期利率代入式(1)计算出债券的理论价格:
其中,PVi 表示理论价格,yt为即期收益率,c为每年的票面利息,M为面值。然后每天对比实际交易价格与理论价格的差值,找出价值被低估的债券来构建投资组合,从而获得较高的收益。而准确计算债券的理论价格就需要构造出利率期限结构。
三、实证分析
(一)Bootstrapping构造利率期限结构的方法
利用付息债券构造收益率曲线,“解鞋带”的一般方式是:假设市场债券均按年付息,第一年的即期利率s1就等于市场上一年期的到期利率。
利用式(3),以此类推计算出s1,s2…,sn,其中Pn为第n年到期的债券的市场价格。已知市场上不同期限的市场价格和n-1个即期利率,就可推算出完整年份的即期利率。
但是在我国交易所上市的债券品种还不是很齐全,对应同一时点剩余期限为1,2,…,n这些年限的债券很难找到,且还需要其他的数据构造出一条平滑的收益率曲线,因此我们使用解鞋带方法和Nelson-Siegel模型结合的方法。
先通过0-1年期限的短期债券计算出到期收益率,也即是即期收益率,再用解鞋带的方法以此推导出(i,i+1)年间的即期利率,接着用Nelson-Siegel数值拟合的方法插值得到0-i年间的平滑的收益率曲线。
(二)Nelson-Siegel模型
采用Nelson-Siegel(1987)模型推导利率期限结构的方法是:假设t时刻期限为μ的即期收益率为yt(μ),满足下列关系式:
其中λt,β0,β1,β2为待估计参数值,εt(μ)代表误差项,β0代表截距项,当期限趋于无穷大时yt(μ)趋向于β0,因此β0被视作期限结构中的长期利率;β1代表斜率项,当期限趋于0时yt(μ)趋向于β1,因此β1被视作期限结构中长短期的利差;β2代表曲率项,被视作中期利率;λt的值决定了β1,β2的衰减速度。
比較普遍的Nelson-Siegel模型估计方法是最小化所有债券的实际交易价格与理论价格之差的加权平方和,即:
其中,Pi表示之前的实际交易价格,PVi表示估计出的理论价格,为了使所有的债券赋予的权重相等,采用ωi=表示第i个债券的权重。
综上,利用Bootstrapping方法结合Nelson-Siegel模型可以构造一条光滑的利率期限结构。
(三)实证结果
本文选用2020年5月8日在上海债券交易所的交易的174支记账式国债的数据,剔除5个极端数据外,选用169支10个标准期限的记账式国债的2020年5月8日的交易价格和到期收益率作为样本数据,本文的数据来自于上海证券交易所网站,其中债券的价格采用的是全价。
从整理的样本数据中可以看出,即使相同期限的到期收益率变化幅度也较大,因此可以根据利率期限结构计算该债券是被低估还是被高估,通过卖出被高估的债券,买入被低估的债券,实现相同风险下较高的收益率。
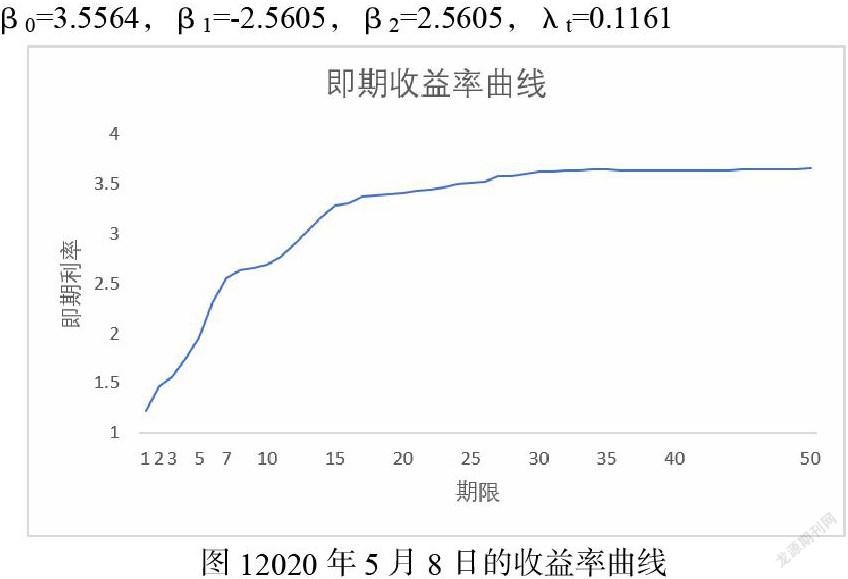
采用样本数据剩余期限推导收益率曲线,综合上述的推导方法得到利率期限结构。根据Nelson-Siegel模型估计出的参数为:
通过把上述参数代入式3得到即期收益率公式,也即得到利率期限结构。从图1中可以看出,利率期限结构虽然局部有小的波动,但整体是向上倾斜并上凸的,说明长期利率是高于短期利率的。这符合市场上流动性偏好的假设,即投资者对期限较长的债券要求风险溢价的。
将其应用到收益率曲线策略中便可以准确计算债券的理论价格,通过对比债券的理论价格与交易价格找到被低估或被高估的债券,有助于投资者构造出优化的债券投资组合。
四、研究结论
本文通过bootstrapping方法和Nelson-Siegel模型结合的方法擬合出利率期限结构,从而对国债的收益率进行预测,同时对债券进行准确定价。主成分分析法发现我国国债利率期限结构的变动的影响因素比较繁多,但是主要影响因素有三个,其中水平因素的解释能力为87.32%,斜率水平的解释能力为11.38%,曲率的影响因素为0.49%。为了防止利率的平行和非平行移动风险,传统的利率免疫策略已经并不能满足,因此投资者可以通过研究收益率曲线的动态变化,使用收益率曲线变动策略来对冲债券投资组合所面临的利率波动风险。
参考文献
[1]信怀义.基于免疫策略的债券投资组合实证研究[J].经济与管理,2017, 31(01):51-57.
[2]彭安兴,申长青.证券投资收益和风险的期限结构研究[J].经济研究导刊,2017(36).
[3]孙明,汪玮.组合证券投资决策分析[J].长春大学学报,2019(29):44-48.
[4]刘代民.我国高收益债券的配置价值及投资组合收益测算[J].债券实务,2020(9):68-73.
作者简介
魏瑞洁,女,汉,河南周口,硕士,河北地质大学,金融风险、金融发展和会计信息。

