基于空间插值方法的2021年云南漾濞MS6.4地震仪器地震烈度影响场分析
于江 和仕芳 卢永坤 庞卫东 罗伟东 钟玉盛


摘要:基于2021年云南漾濞MS6.4主震预警台网地震动数据,使用多种空间插值方法探讨获得最优仪器地震烈度影响场,并与宏观地震烈度调查结果进行对比分析。结果表明:基于指数模型变异函数的普通克里金插值法获得的仪器地震烈度影响场与宏观地震烈度具有较好的一致性,能够反映实际地震烈度空间总体影响场范围及特征;除了两者因概念和属性不同而造成的影响场差异之外,台站分布、场地条件、空间插值方法、前震和余震震害叠加等因素也是导致本次地震影响场差异的主要原因。
关键词:仪器烈度;地震烈度;空间插值;预警台网;漾濞MS6.4地震
中图分类号:P315.9 文献标识码:A 文章编号:1000-0666(2021)03-0414-08
0 引言
地震烈度是衡量地震对地表和工程建筑结构影响和破坏程度的重要参数。在破坏性地震发生后快速评定地震烈度影响场可以为开展地震应急救援、力量部署、灾害损失评估等工作提供重要的科学依据(周光全等,2006;卢永坤等,2019;张建国等,2012)。传统的宏观地震烈度評定是建立在人工调查的基础上,根据多种地震宏观影响后果来评定地震烈度,往往花费较大的人力物力、耗时较长(田秀丰等,2020)。为了满足震后应急快速决策的需要,利用强震动台网观测记录计算仪器地震烈度获取地震烈度影响场的方法逐步发展起来。
仪器地震烈度是指根据仪器观测记录计算得到的地震动强度,并能直接反映地震的影响程度,具有直观、简便、快速等特点(金星等,2013;刘如山等,2021)。近年来,随着国家地震烈度速报和预警项目的建设,我国大陆地区正在布设数千个速度计台站和上万个加速度计台站,其中部分已投入运行,极大地提升了目前地震动观测台站的数量和密度,使得震后利用高密度预警台网仪器烈度进行空间插值快速获取有效的仪器地震烈度影响场成为了可能。2021年5月21日21时48分34秒,云南省漾濞县(25.67°N,99.87°E)发生MS6.4地震。本次地震是云南地震烈度速报和预警项目建成后发生的首次强震,高密度的预警台网获得了丰富的地震动数据。本文以漾濞MS6.4地震为例,使用预警台网地震动数据,尝试运用空间插值方法获得与宏观地震烈度有较好吻合度的仪器地震烈度影响场,然后将其插值结果与宏观地震烈度调查结果进行对比分析,并进一步探讨仪器地震烈度影响场空间插值修正方法。
1 地震动观测数据
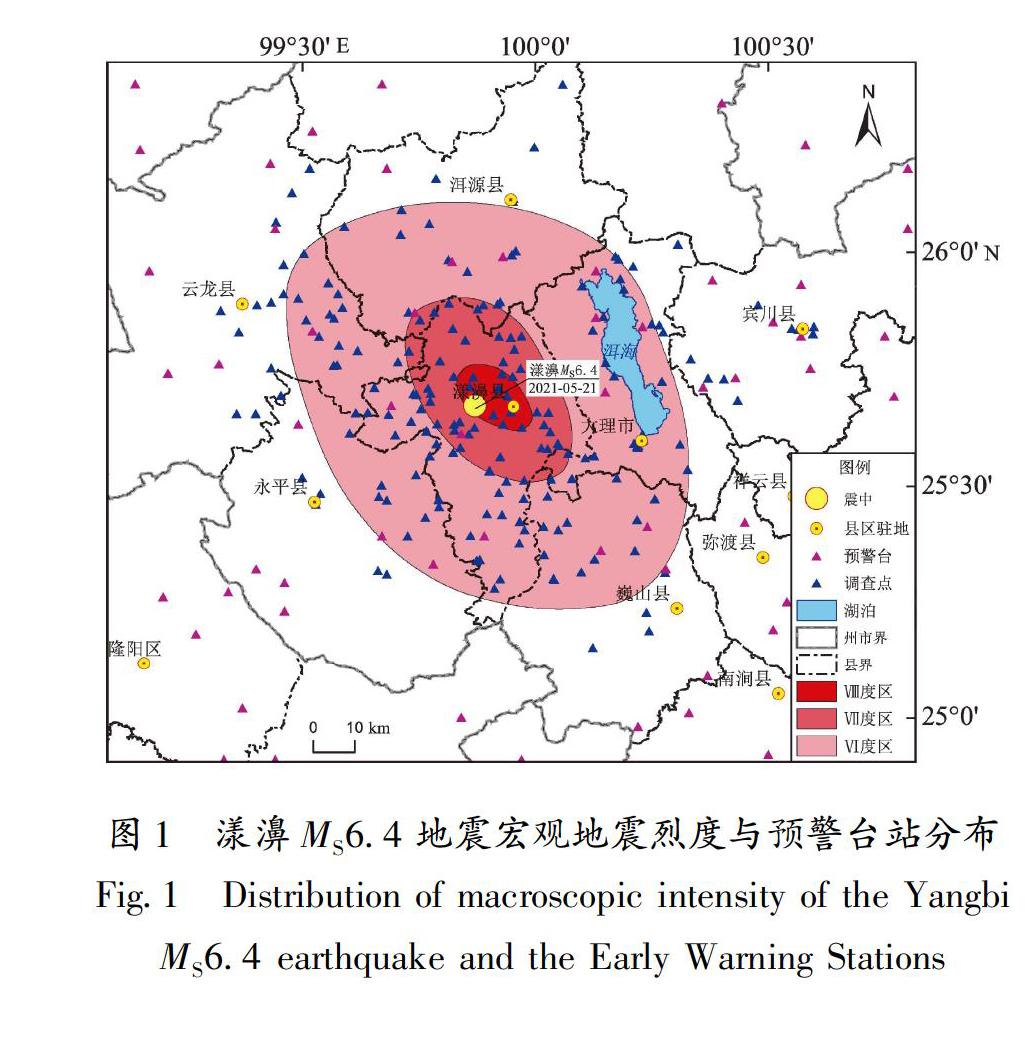
云南省地震局作为国家地震烈度速报和预警项目的先行先试单位,于2020年底完成了全省预警台网的建设工作,省内共建设一千余个台站,其中烈度计站占比80%,重点预警区内台均间距约为10 km,可以达到秒级的地震预警,目前正处于试运行状态。据云南地震台网测定,截至2021年5月29日12时00分漾濞地震序列共发生M≥3.0地震46次,其中6.0~6.9级地震1次,5.0~5.9级地震3次,4.0~4.9级地震13次,3.0~3.9级地震29次。漾濞MS6.4主震350 km范围内共有241个预警台站记录到数据,其中一般站219个、基本站19个、基准站3个。位于漾濞县城的强震动台获得主震记录,最大加速度为719.6 gal。对数据进行初步筛查,剔除了与震中距离较远且相对孤立的台站13个,对两个空间点位重复的台站仅保留了一个与周边站点数据变化范围相近的样本点,最终保留227个台站的地震动数据,最小台间距为2 km,平均台间距约为13 km。图1为漾濞MS6.4地震宏观地震烈度与预警台站分布图。
2 仪器地震烈度影响场空间插值方法
2.1 仪器地震烈度计算
目前,国内外众多学者根据不同地震动特性的地震动参数与地震烈度的关系确定了相应的仪器地震烈度算法(关曙渊等,2020;金星等,2013;Wu et al,2003;崔建文等,2006)。《中国地震烈度表》(GB/T 17442—2020)给出了我国现行仪器地震烈度的计算流程及其定量化测定方法,在对数据进行基线校正、记录转换、数字滤波后,三分向合成地震动参数计算公式如下:
PGA=maxa2(ti)E-W+a2(ti)N-S+a2(ti)U-D(1)
PGV=maxv2(ti)E-W+v2(ti)N-S+v2(ti)U-D(2)
根据式(1)(2)分别计算IA、IV值:
IA=3.17lg(PGA)+6.59(3)
IV=3.00lg(PGV)+9.77(4)
最后根据IA和IV值计算仪器测定的地震烈度II为:
II=IV IA≥6.0且IV≥6.0IA+IV2, (IA<6.0且IV<6.0)(5)
式中:PGA为合成地震动加速度记录的最大值,单位为m/s2; PGV为合成地震动加速度记录的最大值,单位为m/s; a(ti)为ti时刻点合成的三分向加速度值; v(ti)为ti时刻点合成的三分向速度值;下标E-W、N-S、U-D分别表示东西方向、南北方向、垂直方向。
2.2 空间插值方法选取
空间插值是一种通过离散空间数据计算未知空间数据的方法,一般分为确定性方法和地质统计学方法两类(李海涛,邵泽东,2019)。
确定性插值方法是基于已知样本点之间的相似程度或者整个曲面的光滑性来创建一个拟合曲面。主要有反距离权重法趋势面法、样条函数法等;其中反距离权重法作为一种精确插值方法,算法简便易行,当样本数据分布均匀、密度较高足以反映局部差异时具有较好的插值精度(朱求安等,2004;张海平等,2017)。
地质统计学插值方法是利用样本点的统计规律,使样本点之间的空间自相关性定量化,从而在待预测的点周围构建样本点的空间结构模型,比如克立金插值法。克里金插值法作为地质统计学的主要内容是一种以变异函数理论和结构分析为基础,在有限区域内对区域化变量进行无偏最优估计的一种方法,一般分为普通克里金、简单克里金、协克里金、泛克里金、指示克里金等(牟乃夏等,2012;郑向向,帅向华,2013)。
克里金插值法与反距离权重法类似,两者均通过已知样本点权重来求得未知样本点的值,可统一表示为:
Z(x0)=∑ni=1λiZ(xi)(6)
式中:Z(x0)为未知样本点的值;Z(xi)为未知样本点周围的已知样本点的值;λi为第i个已知样本点对未知样本点的权重;n为已知样本点的个数。
相对于反距离权重法只考虑已知样本点与未知样本点的距离远近,克里金插值法还通过变异函数和结构分析,考慮了已知样本点的空间分布及与未知样本点的空间方位关系,能较好反映客观地质规律。其次,地质统计学方法的插值精度与选择的变异函数模型密切相关,常用的变异函数理论模型有圆形模型、球形模型、指数模型、高斯模型等(汤国安,杨昕,2012)。
本文基于以上两类插值方法基本原理,考虑到此次漾濞地震具有较密集的预警台网数据,为寻找最优空间插值方法,分别选择反距离权重法和普通克里金法对离散仪器烈度值进行空间插值。
通常在插值前需要根据所选的空间插值方法,对样本数据分布特征、内在规律性以及趋势效应等进行分析,验证确定权重系数及相关参数或选择合适的变异函数模型,从而提高空间插值的准确率。在使用地质统计学方法分析时,首先需要对数据是否符合正态分布进行验证,若不符合正态分布,则需对数据进行变换。如图2a为本次地震仪器烈度数据直方图,柱状图整体呈左偏的钟形曲线,显示数据接近于正态分布。正态QQ分布图通常用来评估两个数据集分布的相似程度,图2b显示了该组数据整体延45°方向近似呈直线展布,同样显示数据具有正态分布特征。因而该组数据满足地质统计学要求,可以使用克里金插值方法。
在最优权重或变异函数理论模型选择方面,使用反距离权重法插值时,通过预览输出和对比验证确定插值最优权重为3。使用普通克里金插值方法时,根据步长及步长数选择标准,一般最大步长取值应该小于研究区域采样点之间最大尺度的一半,并通过确定点与最近的相邻要素之间的平均距离来确定步长大小,取步长值为0.169,同时为了满足步长数乘以步长大小的值是所有点之间最大距离的一半左右的经验关系,确定步长组数为12;最后,根据数据空间变量的相关性,普通克里金变异函数理论模型分别选择球面模型、指数模型、高斯模型进行空间插值。
2.3 空间插值结果分析
为了评价不同方法获得的空间插值结果,本文将空间插值结果按照地震烈度值进行分类显示,以空间插值结果与宏观地震烈度的吻合程度作为评价依据,从而判断插值结果的优劣。本次漾濞地震现场共调查了218个居民点的震害情况,确定了本次地震最高烈度为Ⅷ度,Ⅵ度区及以上面积约为6 600 km2,共涉及大理州6个县(市)。图3为反距离权重法和普通克里金法对应的4种仪器地震烈度空间插值结果与宏观地震烈度的对比图。
如图3a所示,使用反距离权重法获得的仪器烈度影响场与实际宏观烈度边界在Ⅷ、Ⅶ度区的东边界拟合度较好,Ⅵ度区拟合度较差。拟合得到的仪器烈度影响场长轴走向不明显,尤其是Ⅶ度区的长轴走向整体呈北东向,与宏观地震烈度差别较大。在巍山盆地东缘存在一个孤立Ⅶ度异常区,该区域仪器地震烈度值明显高于周围仪器烈度值,与宏观地震烈度有所差别。
对于地质统计学方法,不同变异函数理论模型所得到的插值结果差距较大。如球面模型与高斯模型(图3b、c)对高烈度区的插值效果较差,基本没有拟合出Ⅷ度区的范围,仪器烈度影响场边界与实际宏观烈度边界拟合吻合度较差。但其影响场范围的整体形态与实际宏观调查所获得的长轴走向拟合较好,可以明显看出仪器烈度影响场长轴走向为北西向。
从指数模型的普通克里金插值结果可以看出,在高烈度区该方法依旧可以根据仅有的一个高烈度值拟合出较小的Ⅷ度区,在Ⅶ、Ⅵ度区的东南边界插值结果和实际宏观烈度也比较吻合,在Ⅵ度区西南边界可以看出受预警台站间距的影响,仅在有样本数据的位置上与宏观Ⅵ度区边界拟合度较好,其边界呈花瓣状。其影响场Ⅵ度区与Ⅶ度区长轴方向也较明显,与宏观地震烈度相符(图3d)。
结合上述讨论的4种插值结果可知,在极震区内台站数量较少的情况下,产出的仪器地震烈度空间分布图更加依赖于插值算法的适用性,不同的插值方法、参数、变异函数理论模型均会对插值结果造成较大影响。本次漾濞地震仪器地震烈度空间插值方法中基于指数模型变异函数的普通克里金方法的插值结果与宏观地震烈度整体范围及特征吻合度较好,反距离权重法插值结果次之。
3 与宏观地震烈度对比分析
根据基于指数模型变异函数的普通克里金插值方法获得的最优仪器烈度影响场与实际宏观地震烈度进行对比,分析导致其影响场差异的主要因素。
3.1 仪器烈度分布特征
对仪器烈度空间插值结果与宏观地震烈度空间范围进行叠加分析,如图4所示,在宏观地震烈度Ⅵ度区范围内,存在部分仪器烈度值小于宏观地震烈度的情况。Ⅵ度区内共有预警台14个,其中8个预警台仪器烈度值小于Ⅵ度,共有7个预警台位于宏观地震烈度Ⅵ度区的西北部,仅有1个预警台位于东南部。仪器烈度影响场存在沿长轴方向在Ⅷ度、Ⅶ度、Ⅵ度区东南方向面积普遍较大的情况,其原因可能是在震中东南方向地震动衰
减较慢,导致在主震东南侧记录到的仪器地震烈度普遍比西北侧高,且距震中更远。而实际调查的宏观地震烈度则沿长轴方向在微观震中两侧面积相差不大,其原因可能是仪器烈度数据仅为漾濞MS6.4主震产生的地震动强度所计算的烈度值,而漾濞地震除主震以外,前震和余震频发,其中5级以上地震就有3次,宏观地震烈度为主震及多次前震、余震叠加所造成的震害,因而在漾濞地震中同一地区宏观烈度值普遍高于仪器烈度值。
在漾濞地震震中附近仅有漾濞台仪器地震烈度大于Ⅷ度,所以导致仅通过仪器烈度插值获得的Ⅷ度区范围较小,与实际宏观烈度Ⅷ度区范围相差较大。其次,在宏观地震烈度Ⅵ度区南部,受预警台站分布不均匀且密度较低的影响,导致在该处空间插值形成的仪器地震烈度影响场Ⅵ度边界呈花瓣状,与实际调查烈度存在一定差异。可见台站密度和分布均匀程度是造成仪器地震烈度与宏观地震烈度差异的另一个影响因素。
由于宏观地震烈度反映的是震害水平的综合指标,影响因素较多,且在综合制图中有平均化的趋势,因而其影响场边界更为均匀光滑,而仪器烈度值则直接由观测的地震动记录计算得到,两者在概念和属性上存在一定差异,因而两者的影响场分布存在差异是不可避免的。
3.2 观测台站场地局部特征
震区属横断山滇西高山峡谷区,地形起伏较大,现场调查发现,震害情况受地形、场地影响较大。通常现场调查是以居民点为单位对该区域的房屋震害整体情况进行评估,而预警台记录的仪器烈度值则反映的是台站所处区域的场地地震动特征。因目前大部分烈度计与通信基站合作架设,其周边地形及场地条件可能往往与居民点所在的环境有所不同,从而造成仪器烈度值与实际调查结果有一定的差异。
在地形起伏缓和、场地覆盖层较厚的地区,场地的放大作用对仪器烈度具有较明显的影响。图4中在Ⅵ度区东南部,巍山盆地东缘大仓台(震中距47 km)仪器烈度值为7.1,而位于其西南侧山区马鞍山台(震中距43 km)仪器烈度值仅为5.9。在地形起伏较大的山区,台站周边场地通常覆盖层较薄,而居民点通常位于平缓的坡地、谷地等覆盖层相对较厚的地方,从而导致仪器烈度值往往低于实际调查烈度值。关坪台位于Ⅵ度区西北部,台站架设在覆盖层较薄的坡地上(图5a),本次记录的仪器烈度值仅为4.1,而在其北侧、东侧约2 km的关坪村旧街小组与自新村实际宏观烈度值均为Ⅵ度(图5b),两者烈度值相差较大。另外,台站与居民点实际所处的地形地貌对震害情况也有着明显的控制作用,往往造成两者烈度值的差异。
4 仪器烈度影响场修正
本次漾濞地震在仅使用预警台网仪器地震烈度进行空间插值所获得的Ⅵ度至Ⅷ度影响场与宏观地震烈度仍有一定出入,尤其是在Ⅷ度高烈度区台站数量很少的情况下,两者差异更为明显。为了获得更加符合实际灾情的地震烈度影响场,可动态利用有效数据对插值参数或样本数据进行修正。
仪器烈度影響场快速评估通常在震后5 min以内进行,此时可以根据主震震级及其烈度衰减关系,考虑断层走向,初步确定影响场长轴方向,调整空间插值参数,针对极震区观测台站较少的情况,可以增加微观震中点作为高烈度区样本数据,修正仪器烈度影响场。震后24 h,可以根据现场实际调查结果,补充震中高烈度区样本点、台站分布空区与边界控制样本点,结合余震分布方向或余震精定位数据,优化仪器烈度影响场长轴方向,修正仪器烈度影响场。根据漾濞现场第一天实际调查结果,在仪器烈度样本数据基础上,补充Ⅷ度区样本点,以及在Ⅵ度区、Ⅶ度区台站空区及控制边界补充样本点,结合余震分布优势方向,使用基于指数变异函数的克里金插值方法获得修正后的地震烈度影响场。从图6可见,经过修正优化后的仪器地震烈度影响场与宏观地震烈度更为接近,显示出较好的修正效果,可以为现场宏观地震烈度调查工作部署提供依据,如第二天可以在Ⅵ度区西北和东南空区方向部署力量,从而促进现场工作开展。
5 结论
本文利用多种空间插值方法探讨获得漾濞地震最优仪器地震烈度影响场,并与宏观地震烈度调查结果进行对比分析,得到以下结论:
(1)在本文讨论的4种方法中,最优空间插值法是基于指数模型变异函数的普通克里金插值法,其仪器地震烈度插值结果与宏观地震烈度整体吻合度较高。
(2)仪器地震烈度与宏观地震烈度影响场的差异主要受台站分布、场地条件、空间插值方法、前震和余震震害叠加等因素的影响。同时,由于仪器地震烈度与宏观地震烈度的概念、属性和物理意义不同,因而两者影响场的分布存在一定差异也是不可避免的。
(3)基于预警台网的仪器地震烈度影响场较好地反映了本次漾濞地震宏观地震烈度长轴方向与地震动衰减方向,真实地反映了地震动强弱的空间范围,与传统地震烈度调查相比,具有速度快,范围广等优点。
(4)针对本次地震仪器烈度与宏观烈度分布差异,可以通过动态利用有效数据对插值参数或样本数据进行修正的方法来进一步改进仪器地震烈度影响场分布图的绘制。
本文在撰写过程中得到了中国地震局昆明地震预报研究所崔建文研究员的指导和帮助,使用了云南地震台提供的漾濞地震预警台网数据,在此表示衷心感谢。
参考文献:
崔建文,李世成,高东,等.2006.云南分区地震动衰减关系[J].地震研究,29(4):386-391.
关曙渊,单振东,马荣.2020.日本仪器烈度计算3种方法对比[J].地震科学进展,50(8):20-24.
金星,张红才,李军,等.2013.地震仪器烈度标准初步研究[J].地球物理学进展,28(5):2336-2351.
李海涛,邵泽东.2019.空间插值分析算法综述[J].计算机系统应用,28(7):1-8.
刘如山,熊明攀,马强,等.2021.基于仪器地震烈度的变电站高压电气设备易损性研究[J].自然灾害学报,30(2):14-23.
卢永坤,周洋,代博洋,等.2019.2018年云南墨江5.9级地震房屋震害特征与烈度评定[J].地震研究,42(2):172-178.
牟乃夏,刘文宝,王海银,等.2012.ArcGIS 10地理信息系统教程[M].北京:测绘出版社.
汤国安,杨昕.2012.ArcGIS地理信息系统空间分析实验教程[M].北京:科学出版社.
田秀丰,张卫东,袁洁,等.2020.汶川8.0级地震仪器烈度与宏观烈度对比分析[J].地震工程学报,42(5):1225-1231.
张海平,周星星,代文.2017.空间插值方法的适用性分析初探[J].地理与地理信息科学,33(6):14-18.
张建国,周光全,崔建文,等.2012.宁洱MS6.4地震考察研究综述[J].地震研究,35(1):151-155.
鄭向向,帅向华.2013.基于地质统计方法与DEM的地震灾情空间插值研究[J].地震学报,35(4):573-583.
周光全,非明伦,施伟华.2006.1992—2005年云南地震灾害损失与主要经济指标研究[J].地震研究,29(2):198-202.
朱求安,张万昌,余钧辉.2004.基于GIS的空间插值方法研究[J].江西师范大学学报(自然科学版),25(2):183-188.
Wu Y M,Teng T L,Shin T C,et al.2003.Relationship between peak ground acceleration,peak ground velocity,and intensity in Taiwan[J].Bulletin of the Seismological Society of America,93(1):386-396.
GB/T 17442—2020,中国地震烈度表[S].
Analysis of the Influence Field of the Instrumental Seismic Intensity of the 2021 Yangbi,Yunnan MS6.4 Earthquake Basedon Spatial Interpolation Method
YU Jiang,HE Shifang,LU Yongkun,PANG Weidong,LUO Weidong,ZHONG Yusheng
(Yunnan Earthquake Agency,Kunming 650224,Yunnan,China)
Abstract
Based on the ground motion data of the Yangbi MS6.4 earthquake recorded by the Yunnan Early Warning Network,a variety of spatial interpolation methods are used to obtain the optimal instrumental intensity influence field,and compared with the results from the macroscopic intensity obtained from field survey.The results show that the influence field of instrumental intensity obtained by the ordinary Kriging interpolation method based on the variogram of the exponential model has a good agreement with the macroscopic seismic intensity,which can reflect the overall range of the influence field and characteristics of the actual seismic intensity.The main reasons for the differences between the instrumental intensity influence field and the macroscopic intensity field are the distribution of stations,site conditions,spatial interpolation methods,and the superposition of foreshocks damage and aftershocks damage.
Keywords:instrumental intensity;earthquake intensity;spatial interpolation;the Yunnan Early Warning Network;the Yangbi MS6.4 earthquake

