建筑物地基沉降的规律与特征分析
——基于多个著名建筑物与城市地面出现的沉降为案例
张振海
(上海新荣阳投资控股集团,上海 200082)
0 引 言
地基沉降与变形是整个地基基础工程中众多难题之一,至今尚未完全解决此问题。特别是中国的地基工程方面,在设计的根源方面就存在一些缺陷,对沉降方面的重视程度不足(相比更重视承载力的方面),此问题是基于历史的原因,在新中国成立后,于1954年引进了前苏联地基规范《天然地基设计暂行规范》(规结7-54),此规范对后期中国地基设计方面影响巨大。由于此规范不考虑地基的沉降控制,因此对此后的中国地基工程在设计方面的演变与发展产生了许多负面的影响[1]。
(1)公式表达
地基沉降主要发生在土壤结构中,其沉降一般分为3个部分:瞬始沉降、固结沉降和蠕变沉降,用公式(1)表达为:

式中:Sd为瞬始沉降,系第一阶段的土壤剪切应变形成;Sc为固结沉降,系第二阶段的土壤孔隙水在排出后及消散的过程中其骨架产生变形而形成;Ss为蠕变沉降,系第三阶段的孔隙水在消散后及其骨架本身的蠕动变化而形成。
(2)3个阶段
3个部分的沉降按其发生的时间顺序,可以划分为3个阶段:第一阶段表现的主要形式为瞬始沉降(固结与蠕变也同时发生,即3种沉降同时发生),时间发生在建设开始至建设完成,约在2年期间内完成(占总沉降量约60%左右)。第二阶段表现的主要形式为固结沉降(蠕变也同时发生,即两种沉降同时发生),时间发生在建设完工后 1~5年之间。第三阶段表现的形式为蠕变沉降(固结也同时发生,即两种沉降同时发生),时间发生在建设完工5年后,最长时间可达千年。如意大利的比萨斜塔,从 1173年建设开始至 2001年纠偏的加固完成;又如中国的虎丘斜塔,从959年建设开始至1981年纠偏时加固完成,此两个著名的建筑物在大约千年的时间内,沉降的现象仍在持续。根据3个阶段的沉降规律,又表现出不同的特征,具体如表1所示。

表1 沉降的分类阶段与特征Table 1 Classification stage and characteristics of settlement
(3)完成时间
到目前为止,基于以下4个方面为依据,地基沉降的科学研究尚未发现有效的证据或者试验可以得出明确的沉降完成时间。
a)抽取样本。根据上海市抽取33幢建筑物为样本,按其沉降观测的统计数据,此33幢建筑物在建成10年后的沉降速度为2.5~3.0 mm/年,没有明显迹象表明沉降已停止[2]。
b)维也纳固结试验。维也纳工业大学的土力学实验室,为了研究土体蠕变变形的持续时间,从1971年开始经过42年的加载至2013年,土体变形仍在继续发展,这种变形只会减速而不会停止,即形成“维也纳固结试验沉降曲线”[3]。
c)著名建筑物案例与统计。统计一些著名建筑物沉降的累计量,从几年到千年的时间中,没有明确显示沉降完成的时间,详见表2所示。

表2 著名建筑物沉降统计表Table 2 Settlement statistics of famous buildings
d)城市地面案例。不但建筑物具有沉降的特征,城市的地面也发生类似的情况而且无明确的沉降结束时间。如雅加达与新奥尔良,其地面由原来高于海平面至目前已低于海平面,如表3所示。
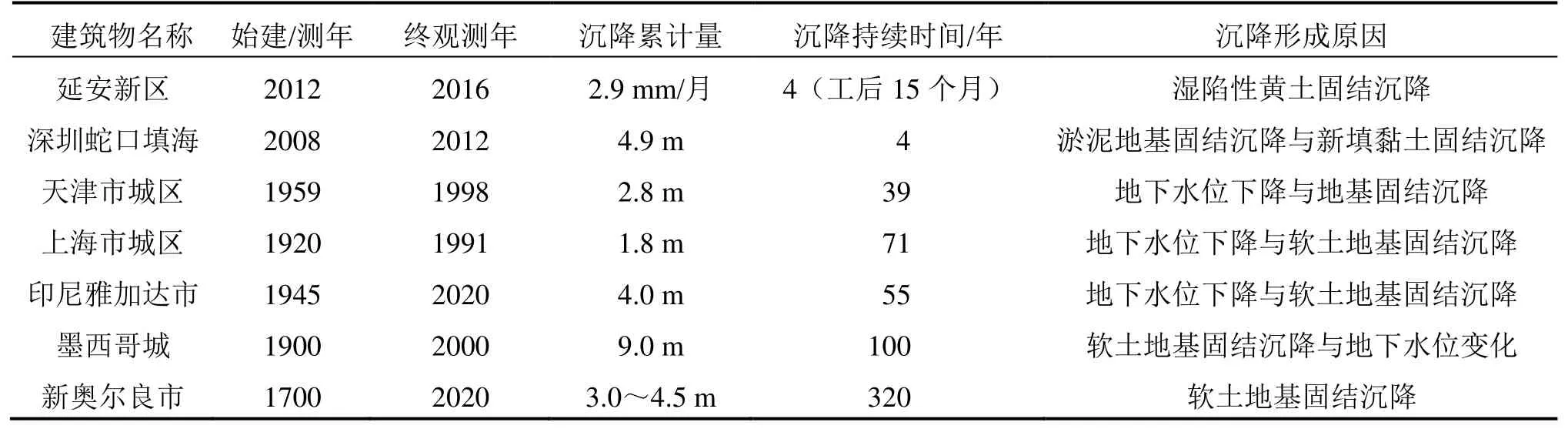
表3 一些城市沉降统计表Table 3 Settlement statistics of some cities
1 计算沉降的方法
1.1 4种计算方法
归纳现行中国国内地基沉降的计算方法主要有4种:弹性理论法、压缩模量(或工程实用)法、经验法(或现场试验法)、数值计算法[4]。其中前3种方法为常用类型,而第4种方法由于计算的复杂性以及模型的不准确性,导致其使用受到限制,但此类型在理论分析上较为精确,因此用于理论论证上具有优势。4个类型中又分为各自的子类型,并各具特色,如表4所示。

表4 现行地基基础沉降计算的方法分类Table 4 Classification of current foundation settlement calculation methods
表4是归纳与总结近代以来多种国内外计算的方法,其中最具有代表性的方法有分层沉降总和计算法与桩基础沉降计算法,阐述如下:
(1)分层沉降总和计算法。此方法运用较广泛,其物理意义简单明了,同时计算参数也容易获得,因此在工程界广泛使用。根据e-p曲线,各层土的压缩量公式为:s=(e1i-e2i/1+e1i)Hi。式中:e1i为第i层压缩前对应的孔隙比;e2i为第i层压缩后对应的孔隙比;Hi为第i层土壤的厚度。
(2)桩基础沉降计算法。桩基沉降的常用方法有两种:一是布辛尼斯克实体基础法,将全部荷载集中作用在桩尖平面上,以桩尖平面为半无限元表面,与浅基础一样用分层总和法计算,桩尖平面以上中的应力与应变和桩土的相互作用全部忽略不计;二是明德林法,将每根桩的荷载分为端阻力与侧阻力,根据荷载或者统计经验确定所占的比值,将端阻力假定沿桩身矩形分布或三角形分布,将逐根桩的应力叠加,算出地基中的附加应力,再利用分层总和法计算桩基沉降。
1.2 计算结果误差的原因
地基沉降计算的结果,不论采用任何一种类型的计算方法,在目前阶段尚不能达到完全准确,都存在着一定程度的误差,形成的主要原因有两个:
(1)偏面性。以最常用与最初研究形成的弹性理论与压缩模量两种方法为例,其参数只能反映土壤体积压缩产生的变化,而不能反映土壤的剪切变化,因而需要进行扩大性的修正,扩大的系数为1.1~1.4倍,这样才能弥补由于剪切变化产生的沉降部分的数量。
(2)扰动性。土壤参数均来自取样后送达实验室进行,必然存在从原始现场到实验室样本的扰动,而土壤扰动后产生力学性能变小,因而需要进行缩小性的修正,缩小的系数为0.2~1.0倍,这样才能减小由于扰动造成的沉降部分量。
2 地基沉降与时间的相关性
2.1 定性分析
按表1所述,瞬时沉降是在约2年的时间内完成,并且此部分沉降的数量往往占到总沉降量的大部分比率,约为60%左右。其后的固结沉降速度放慢,在约 2~5年的时间内完成。最后则是蠕变沉降,此过程非常漫长,达几十年或上百年,甚至上千年。
地基沉降与时间呈非线性的正相关性。总体的规律是先快后慢,反映在坐标轴(时间为横轴,沉降为纵轴)第一象限内为向上凸起曲线,起点位于坐标轴零点,终端无限接近于某一个与水平轴平行的一条直线或到达此直线。
2.2 定量分析
虽然无法精确计算地基沉降与时间之间的关系,但可以按经验法进行两者之间关系的定量计算,如双曲线式的计算方法与对数曲线式的计算方法,可以表示它们之间的数量相关性,如下所述:
(1)用双曲线式的计算方法,其公式表达为:st=(t⁄(a+t))s。式中:st为在时间t(从施工期一半起算)时的实测沉降量;s为待定的地基最终沉降量;a为经验参数。
(2)用指数(对数)曲线式的计算方法,其公式表达为:st=(1−e-at)s。式中:e为自然对数的底;a为经验参数。利用实测的s-t曲线后段资料,可求得地基最终沉降量s值,并可推算任意时间t时的沉降量st。
3 沉降的弊端与有效利用
3.1 沉降的弊端
建筑物或者地面的沉降一般产生负面的影响,往往会产生建筑物功能的丧失,甚至扩大到对城市范围内的不良影响,阐述如下:
(1)对建筑物的影响。建筑物沉降产生的影响,总体是以负面为主。建筑物直接受力在土壤上或软土地基上,既使是承载力满足荷载的要求,但如果沉降超出正常范围,也会产生一些不良的影响,如建筑物凹陷低于周围地面、墙体开裂、结构受到破坏、甚至会导致建筑物倒塌。
以上海展览中心为例。从1954年(建造时点)—2000年(测量时点),共46年期间内沉降量达到1.9 m,严重影响建筑物的正常使用。又如比萨斜塔、虎丘斜塔则面临倒塌的风险,而加拿大特朗斯康谷仓群则是直接倒塌。
(2)对城市的影响。沉降不但影响建筑物,甚至影响到更大的城市范围,如中国上海城区、中国天津城区、美国新奥尔良市区、墨西哥城等城区则是由于沉降的原因造成一些不利的因素,特别是印尼雅加达市则面临着首都被迫迁移的问题。
3.2 有效利用
相反掌握了沉降的规律,也可以利用沉降进行兴利除弊。如中国延安新区挖土填沟与深圳蛇口填海是利用沉降的规律进行地基的处理;又如墨西哥特斯科科湖地区公园,也是利用了沉降的原理,利用抽水降低水位形成一个湖泊基础坑体(连续5年抽水,使地面下降4 m),而不是采用挖土的方式(后者的成本远远高于前者)[5]。
以中国延安新区为例。此新区挖了 33座山峰填入到相应的沟壑中,其中最大填方深度达120 m,总土方量近1×108m3。从2012年4月份开始,通过“削山、填沟、造地、建城”,计划用 10年时间,最终造出78.5 km2的新区建设面积,相当于在城市周边的山头与沟壑地带建造了一个两倍于原有老城区的新城。它是目前中国湿陷性黄土地区最大的岩土工程,整个场区填方区与挖方区面积均等,且具有自重湿陷性。填方区与挖方区呈现“齿牙交错”的无规则带型分布。采用的处理方法有换土垫层法、强夯法、灰土挤密桩法、预浸水或桩基础等多种方法。目前新城建设后使用功能正常,说明利用沉降规律进行建设是成功的。
4 防范超量沉降的方法
基于原状土壤沉降数量大且不易控制的原因,可以进行预留沉降落差量的被动方法——按黏性土压实系数K的取值0.90~0.95之间,防范沉降量的数值按计算或填土高度 0.5%~5%之间进行预留(即将填土高度高出设计平面的数量值),则此高出部分,可以在沉降相对稳定后,用于抵消沉降量,达到设计所需要的平面[6]。
而更重要的则是需要预防为主的办法,常用的方法有4个类型:采用预压法、置换法、搅拌法、桩基础等方法[7],如表5所示。

表5 防范超量沉降的方法Table 5 Methods to prevent similar quality accidents
随着建筑物高度的增长、荷载的加大,采用桩基础可以增大荷载且同时控制沉降,起到了双重功能的作用。特别是采用超长桩(L>50 m)的超高层建筑,其基础沉降一般都在0.06~0.1 m,沉降表现在(断)平面上也比较均匀。实测的沉降量也比按规范规定计算出的沉降量数值小。如以上海金茂大厦为例,实测沉降量为0.082 m,而理论沉降计算值为0.085 m,两者接近并且实测值小于理论计算值,控制的效果超级优秀。
5 非均匀沉降的补救措施
既有建筑物由于沉降产生倾斜后常用纠正加固的方法,本文归纳为以下9个类型,并且在相关案例中进行实践性的应用,如表6所述。
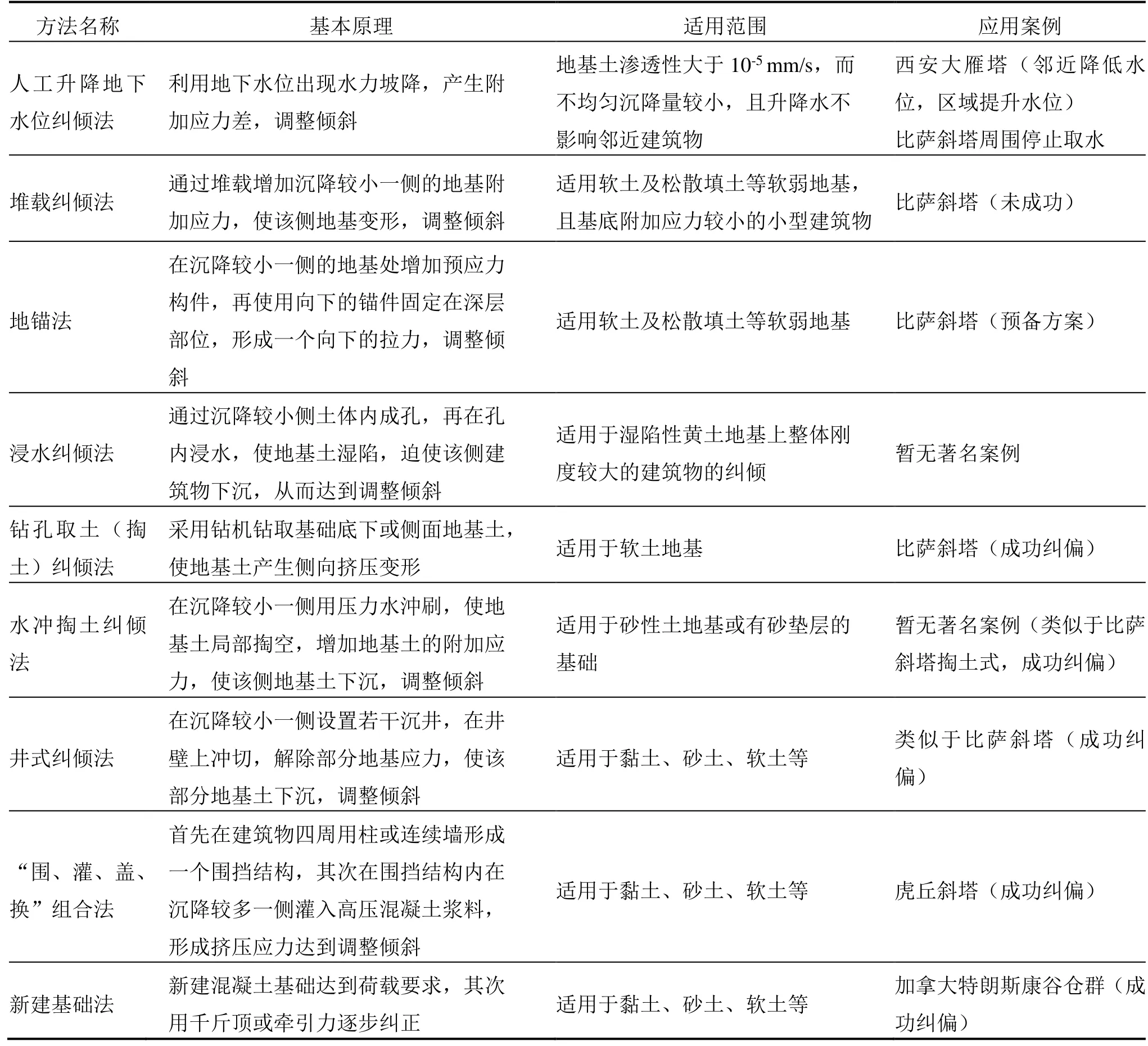
表6 纠偏建筑物常用的方法与其相关的机理Table 6 Common methods and related mechanisms of deviation correction of buildings
建筑产生倾斜后,需要对产生倾斜的原因进行分析,以及选择适当的方法进行纠偏,总结得出需要因地制宜或多种方法综合运用,以著名的比萨斜塔与苏州虎丘斜塔为案例,分析如下。
5.1 虎丘斜塔案例[8]
纠正或补救的措施分为4个部分:“围、灌、盖、换”,具体如下:
(1)塔周围浇筑混凝土桩:在离塔外侧约2.9 m开挖直径为 1.4 m的孔洞,深约 3.7~10.68 m,控制桩深入到岩层不小于0.8 m。用钢筋混凝土现浇 44根混凝土桩,桩与桩外侧相切形成一个整体式篱笆桩墙体,上部配圈梁(宽1.4 m×高0.4 m),将桩连为一个整体。
(2)灌水泥浆:在围桩范围内钻161个孔(孔钻入岩石内0.1 m,平均深度比桩略浅),直径为70与 90 mm 两种,水泥灌浆的压力控制在 0.2~0.3 MPa(在塔体近端处控制在0.15 MPa),灌浆量达26.64 m3,是钻孔体积的4倍,在围桩范围内形成一个整体的密实体。
(3)盖钢筋混凝土板:采用0.40~0.65 m变厚钢筋混凝土板(在沉降大的一侧采用0.65 m厚板,相反在另一侧采用0.4 m薄板),盖板起到上部加固与防水渗入的双重功能。盖板分为 33块进行开挖与跳花式施工,在塔身一侧上环顶住塔身基础,在圈梁一侧钢筋连接,目的是盖板起到支撑与连接的作用。盖板的排水坡度控制在37°。
(4)置换碎砖:将砖砌体的破碎部分进行更换,原则是“修旧如旧、维持原状”,即仍采用原塔身同样颜色的青砖,强度需要达到20 MPa以上。目的是将破碎部分经修缮后达到与原有砖筑体的强度与稳定性要求。
5.2 比萨斜塔案例[9]
纠正或补救的措施分为4个部分:方案、监测、防范、施工,具体如下:
(1)方案:经过8年之久的论证才最终选定纠偏方法:从斜塔的北侧地基下抽出部分沙土,使斜塔的倾斜自然北移。
(2)监测:共架设120部精密仪器,从各个角度和高度严密监测斜塔的动静,从而提供数据用于方案与施工的决策。
(3)防范:为防止塔身发生意外变形或倒塌等情况,采用几条钢索环绕捆住斜塔的二层,向北拉住塔身(即倾斜的反方向)。
(4)施工:抽土采用41条抽土管深度插入20 m深的北侧塔基地下进行,经过一段时间的抽土施工,到2001年6月倾斜角度回到安全范围之内,比萨斜塔的安全性重新得到保障,一个世纪的纠偏愿望终于得以实现。
6 结 论
通过本文分析发现,地基的沉降到目前为止尚未发现有明确完成的时间,只能是无限接近于某一个固定数值,并且随着环境的变化仍会继续发展(可能是良性,也可能是恶性),因此需要在建设的设计与施工过程中进行防范,充分利用其规律与特征,达到趋利避害的目的,防范沉降的发生是一个系统性的工程工作,宜从勘探、设计、施工、工艺、使用等全生命周期进行综合治理,才能达到防患于未然。

