垂直非均布移动轮载作用下沥青路面结构数值分析*

蒋 鑫 陈 戈 王 鑫 武琨璐 邱延峻

(1.西南交通大学土木工程学院 成都 610031； 2.西南交通大学道路工程四川省重点实验室 成都 610031；3.西南交通大学高速铁路线路工程教育部重点实验室 成都 610031)

目前沥青路面结构分析多采用垂直均布静载，无法反映实际轮胎-路面接触应力强烈的非均布特征。针对实际非均布轮载作用的复杂性，胡小弟等[1]运用自主研发的轮地压力静态测试装置对多种轮胎的接地压力分布与路面力学响应进行了测验，并归纳了不同车型轮胎的面积折减率、横向压力分布等规律；A.Said等[2]根据轮胎压力实测数据提出了高压轮胎、低压轮胎接地应力的非均布简化方程；Jiang等[3]运用三维有限元法分析了不同类型垂向非均布静载对沥青路面力学响应的影响，比较了均布荷载与垂向非均布荷载下沥青路面结构力学响应的差异；De Beer等[4]运用半解析有限元法对比了实测非均布垂直荷载与均布荷载对薄沥青路面力学响应的影响；黄志义等[5]运用连续有限层法对实测非均布荷载与均布荷载进行了黏弹性对比分析。

这些研究着力于轮胎接地压力分布形状、静态力学响应计算及均布与非均布荷载的对比，但对相同轮载大小、不同接地应力分布作用下的力学响应规律缺少专门研究。基于上述背景，本文试图探讨垂直非均布移动轮载作用下沥青路面结构力学响应的变化规律，从而为道路行车试验时科学加载及路面结构精细化分析提供参考。

1 3D-Move Analysis软件数值建模关键技术

3D-Move Analysis系美国The University of Nevada, Reno(UNR)开发的一款基于三维连续有限层法的沥青路面结构电算软件。前期研究表明，其在沥青面层黏弹性及复杂荷载考虑等方面均具有独到之处，下面结合本文欲分析的问题，就建模中的关键技术做扼要介绍。

1.1 荷载复杂性的考虑

3D-Move Analysis 程序实施的具体步骤如下：①将复杂的荷载离散化成单元荷载；②利用傅里叶展开公式将单元荷载转化为谐波分量；③通过叠加原理得到X和Y方向的总荷载傅里叶级数。表面荷载在平面上被分为N×M份，荷载在离散时会留下足够大的无荷载作用区域以免对下个周期的加载产生影响。离散化方式见图1，具体转化过程如式(1)～(4)。

(1)

(2)

(3)

(4)

式中：q(x,y,t)为经过转换t时刻的总响应；q(j,k)为坐标(j,k)处单元荷载；m、n为单元荷载所在坐标；Δx、Δy为单元长度；c为行车速度；t为时间。

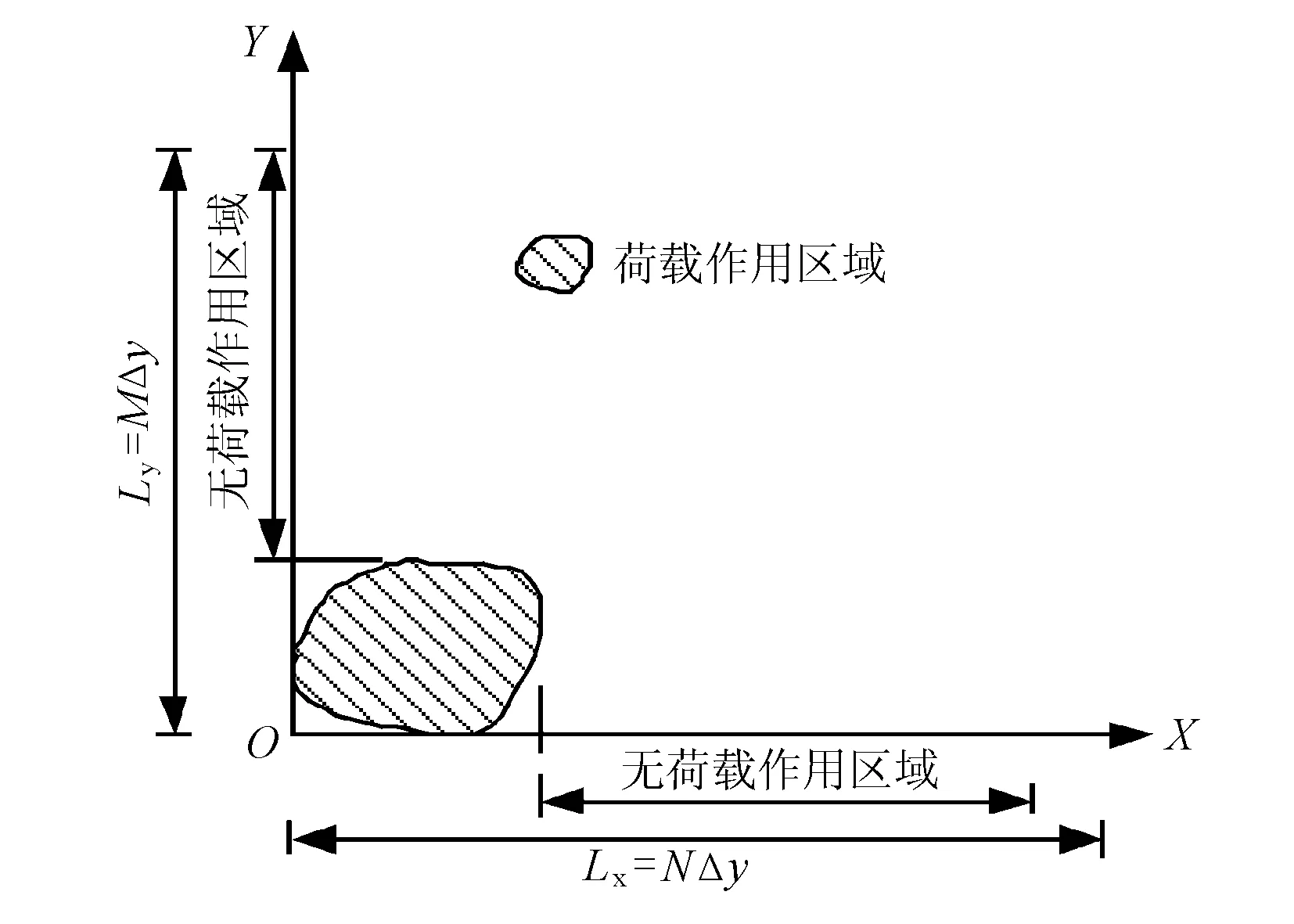
图1 3D-Move analysis程序表面荷载离散方式

该软件因所采用的三维连续有限层法的优势，即通过将表面荷载转化为含时间、速度变量的傅里叶级数，可以很好地考虑表面荷载的移动性、非均布等特点。具体实施时，3D-Move Analysis程序中Δx、Δy单元长度根据自带实测荷载库或用户自行输入确定。

1.2 沥青面层黏弹性的考虑

由于沥青具有黏弹性，其弹性模量依赖于温度和荷载作用时间，直接影响着路面使用性能，国内外学者针对这一特性进行了大量研究，如孔思林等[6]利用三维有限元法对车辆在制动与启动时的力学响应进行了黏弹性分析，确定了沥青材料动态模量模型。

3D-Move Analysis通过在不同模型下构建动态模量主曲线来实现沥青路面的黏弹性分析，程序包含4种主曲线生成模型，即根据试验数据确定动态模量的对称Sigmoidal模型、非对称Sigmoidal模型和Hust-sayegh模型及通过沥青面层混合料本身的特性来预测动态模量的Witczak模型。前3种模型确定沥青面层动态模量主曲线过程如下：①将不同温度、频率下的实测动态模量数据输入模型；②利用时间-温度叠加原理绘制参考温度的主曲线；③利用位移因子，得到分析温度的动态模量主曲线。第4种模型则为预测模型，可通过沥青混合料的级配、体积特性、黏结剂属性等预测指定温度下的沥青模量主曲线。

2 数值分析模型建立

2.1 路面结构组合与材料参数

文献[7]中Example B的路面结构，以沥青面层+级配碎石基层+土基组成的三层式沥青路面结构为例，结构层厚度、材料参数等见图2，其中：E、ζ、υ分别为弹性模量、阻尼比及泊松比。

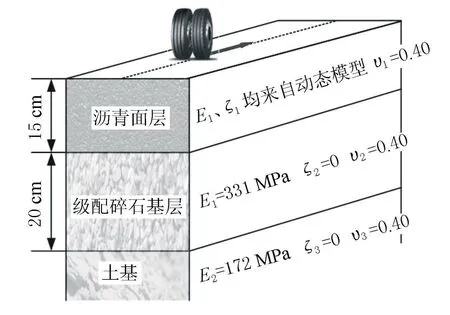
图2 路面结构参数

动态模量计算选择对称Sigmoidal模型，即通过试验测得不同温度、频率下的沥青模量，再用对称Sigmoidal模型将其拟合成动态模量主曲线。主曲线计算方法见式(5)。

(5)

式中：E*为沥青材料的动态模量，psi；α、δ为拟合参数，δ为动态模量的最小值，δ+α为动态模量的最大值，psi；β、γ为Sigmoidal函数的形状参数；tr为参考温度下的荷载作用时间；η为黏度，mPa·s；ηr为参考温度下的黏度，mPa·s。

试验数据下由该模型在温度为25 ℃时生成的沥青动态模量主曲线见图3。

图3 沥青面层动态模量主曲线

2.2 垂直非均布移动轮载

选用3D-Move Analysis程序中自带的Kistler MODULAS数据库中所列荷载。该数据库引用自M.Sime等[8]利用压力传感器测得的多组轮胎接地应力，其中不同车速下的垂向应力分布多达192组，胎压范围为420～1 000 kPa，轮载范围为4.5～62 kN。在Kistler MODULAS数据库中车速V=32 km/h时，GOOD YEAR295/75 R22.5型轮重为25 kN轮胎的接地压强分布见图4，如参照国内现行公路沥青路面设计规范[9]中的BZZ-100双轮单轴标准轴载，可认为前二者胎压偏低，0.69 MPa与0.7 MPa相当接近，而0.827 MPa则可认为胎压偏高。图4a)、b)表明，当胎压偏低时，轮胎接地压强沿胎宽方向呈凹型分布；图4c)属于由低压轮胎到高压轮胎过渡状态，轮胎接地压强沿胎宽方向呈凹凸交错分布；图4d)为胎压偏高时，轮胎接地压强沿胎宽方向呈凸型分布。p=0.517 MPa(低压轮胎)与p=0.827 MPa(高压轮胎)不同车速下的轮胎路面接地应力情况分布见图5、图6。

图4 4种非均布轮载的分布(V=32 km/h)

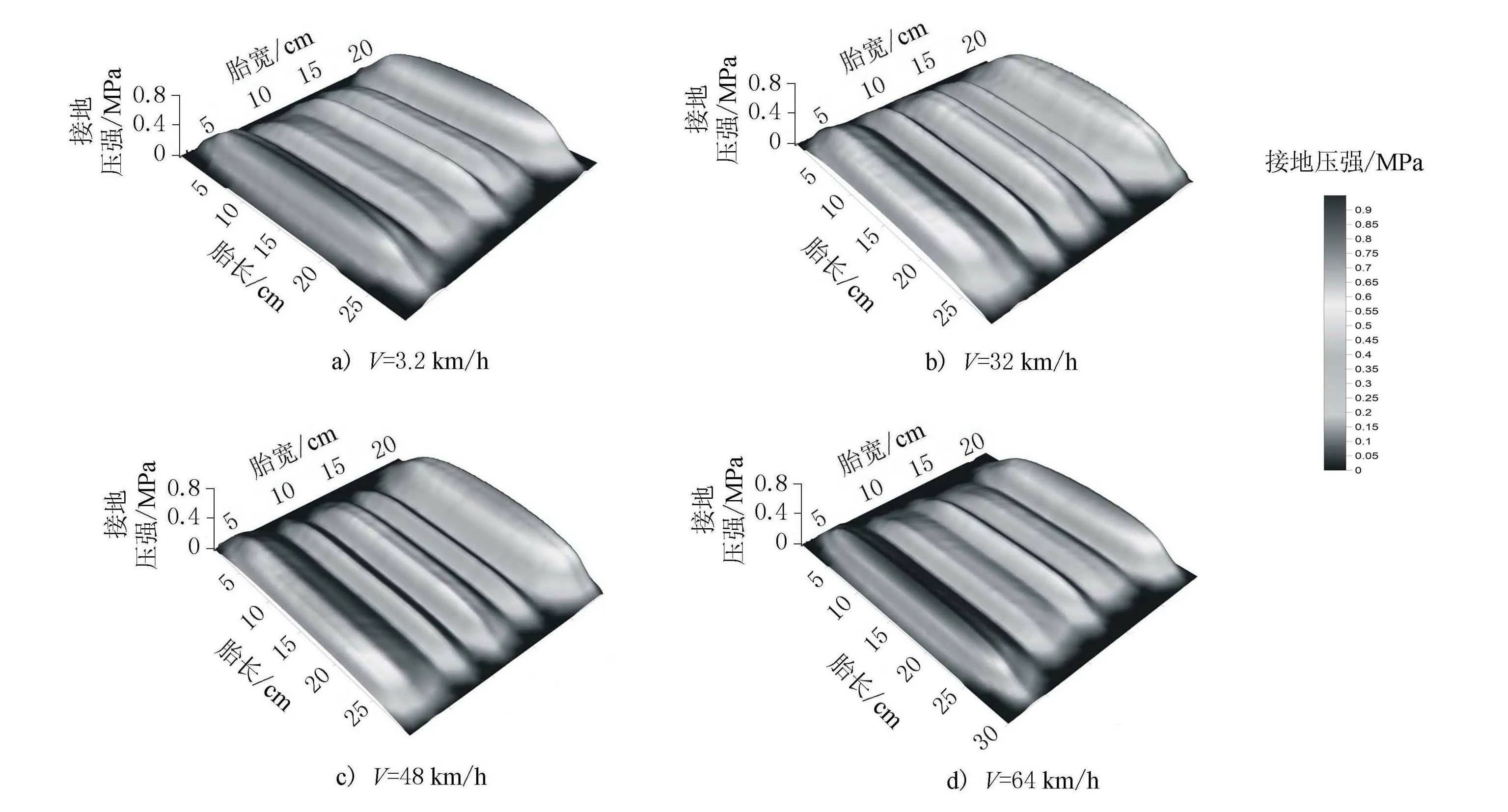
图5 胎压p=0.517 MPa时接地压强分布

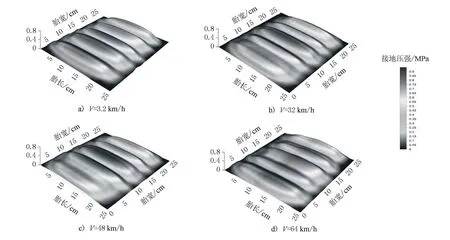
图6 胎压p=0.827 MPa时接地压强分布

3 主要计算结果分析与讨论

3.1 胎压致接地压强非均匀分布的影响

当车速V=32 km/h时，图2所示路面结构土基顶竖向压应变、沥青面层层底行车方向拉应变等力学响应的横向分布分别见图7、图8，同时给出按照文献[9]所述设计轴载，即胎压、接地压强均为0.7 MPa的双圆垂直均布荷载的计算结果以作对比。

图7 土基顶压应变横向分布

图8 沥青面层层底拉应变横向分布

由图7、图8可见，与均布荷载类似，4种不同非均布荷载作用下土基顶竖向压应变沿胎宽均呈单峰状分布，最大压应变的位置始终位于双轮中心处。而沥青面层底拉应变尽管仍呈双峰马鞍状，但行车方向最大拉应变的位置随轮胎接地压强的减小向双轮轮隙中心处转移。在相同轮重非均匀分布情况下，沥青面层层底拉应变与土基顶压应变均随着轮胎接地压强的减小而减小，但二者影响程度有所不同，当非均布荷载胎压从0.827 MPa减小到0.420 MPa时，土基顶最大压应变减少1.72%，而沥青面层层底最大拉应变减少6.67%，轮胎接地压强对沥青面层底拉应变的影响强于土基顶压应变。

进一步讨论轮载非均布情况下轮胎接地压强的高低对沥青面层底最大拉应变发生位置的影响，具体见图9。

图9 最大拉应变变化

由图9可见，当胎压偏高(p=0.827 MPa)或处于高、低胎压过渡时(p=0.690 MPa)，二者沥青面层底行车方向最大拉应变发生于轮胎内与双轮内边缘相距1/8胎宽处，与均布荷载(p=0.70 MPa)最大拉应变位置相似，这可能是均布荷载采用圆形分布，中部集中，与高压轮胎作用下接地应力凸型分布相似；当胎压偏低时(p=0.517，0.420 MPa)，随着胎压减小，轮地接触压强形态发生变化，沥青面层底行车方向最大拉应变位置逐渐向中心移动，胎压低到一定程度后(如p=0.420 MPa)沥青面层层底最大拉应变位置调整为双轮轮隙中心，这说明胎压偏低时沥青面层底最大拉应变的最不利点位变化相对较大。

3.2 车速的影响

在路面温度为25 ℃情况下，p=0.517 MPa(胎压偏低)、p=0.827 MPa(胎压偏高)2种胎压情况与均布荷载车速变化时，土基顶压应变与沥青面层底面行车方向拉应变分布分别见图10、图11。

图10 土基顶压应变横向分布随车速变化

图11 沥青面层层底拉应变横向分布随车速变化

由图10、图11从总体来看，对于土基顶压应变，其最不利点位的位置一直位于双轮中心不发生改变。而随着车速的增加，与均布荷载类似，非均布荷载情况下沥青面层层底行车方向拉应变与土基顶压应变均呈下降趋势，且减小的幅度逐渐变小。这是由于沥青面层的动态模量随着频率的增大而增大，但达到一定值后，其增大的幅度会随着频率的增大而趋于平缓。

不同胎压情况下随速度变化最大拉应变与中心拉应变的数值变化与距离变化关系见图12～图14。由图12～图14可见，当胎压偏高时(p=0.827 MPa)，随着车速增加，沥青面层底最大拉应变位置基本不变，均处于轮胎内与内侧边缘靠近处。当车速为3.2 km/h时，最大拉应变与双轮中心处拉应变相差7.71×10-6，降幅为2.82%，而当车速为64 km/h时，最大拉应变与双轮中心处拉应变相差0.64×10-6，降幅为0.39%，这说明随着车速的增加，当胎压偏高时沥青面层底最大拉应变与双轮中心处拉应变更为接近，均布荷载情况下沥青面层底拉应变的变化规律与胎压偏高时类似。

图12 p=0.517 MPa最大拉应变

图13 p=0.700 MPa最大拉应变

图14 p=0.827 MPa最大拉应变

当胎压偏低时(p=0.517 MPa)，如车辆低速行驶(V=3.2 km/h)，其最大拉应变位置位于轮胎内与内侧边缘相距1/4胎宽处，而随着车速的增加，行车方向最大拉应变位置向中间靠拢，最后调整为轮胎中心处(车速V=48 km/h)。这说明胎压偏低时，车速变化对沥青路面面层层底行车方向拉应变影响更大，但胎压偏高时，车速变化对沥青面层底最大拉应变位置影响并不大。

鉴于路面结构开展现场动测试验时，传感器提前预埋于路面结构内部，并尽量设法控制以轮胎固定位置(一般为一侧轮胎中心处或双轮轮隙中心处)驶过路面内部预埋传感器的正上方，如Middleton等人在开展现场动测实验时将电阻应变片埋设于双轮中心下方0.5 m处以测得水平应变[10-11]。然而上述计算表明轮载的垂向非均匀分布会导致轮胎中心处或双轮轮隙中心处沥青路面结构内动力学响应并非始终保持最大，不能获得真正意义上的最不利力学响应，从而导致路面结构性能预测严重失真。

4 结语

1) 垂直荷载的非均匀分布形式对沥青面层的影响远大于土基。当胎压偏高时致胎宽方向接地压强呈凸型非均匀分布时，沥青面层底最大拉应变位置与均布荷载作用下最大拉应变位置相近；当胎压偏低致接地压强呈沿胎宽方向凹形非均匀分布时，会较大程度地影响最大拉应变位置，且胎压越低，最大拉应变越向两轮中心处靠近。

2) 随着车速增加，与均布荷载类似，胎压偏高或偏低致接地压强非均布时沥青面层底拉应变的横向变化均趋于缓和，在一定速度范围内，胎压偏高致接地压强呈沿胎宽方向凸形分布时沥青面层底的最大拉应变位置变化不大，但胎压偏低导致接地压强呈沿胎宽方向凹形分布时，沥青面层底最大拉应变将向两轮中心处靠近。

3) 如现场试验条件允许，开展沥青路面结构现场动测时，可根据垂直非均布移动荷载的性态合理确定加载位置，以更准确地捕捉不同情况下力学响应，尤其是沥青面层底拉应变的最不利值。