具有外部干扰的耦合时滞神经网络固定时间二分同步

陈苏浩， 刘小洋， 谢春丽， 王书芹

(江苏师范大学 计算机科学与技术学院， 江苏 徐州 221116)

人工神经网络是一种模仿生物大脑神经特征而模拟出来的一种算法模型，它具有自适应、自组织等特点，被广泛应用于图像识别、信息安全、语音处理以及生物研究等领域.其中，耦合神经网络的同步作为网络群集行为的一种重要表现，受到了广泛的关注，已成为当前学术界研究的热点.目前，常见的同步有完全同步、渐进同步及指数同步等[1].

值得注意的是XU C.等[1]所讨论的同步是当时间趋于无穷大时系统才能趋于同步，其在实际应用中具有一定的局限性.人们通常希望同步目标能够在有限的时间内达到.例如，LIU X. Y.等[2]研究了具有连续或非连续激活函数的耦合神经网络有限时间同步问题，在切换拓扑结构之下，借助有限时间稳定性理论，获得了当激活函数与控制器都不连续情形下的有限时间同步判据.

有限时间同步同样存在一定的局限性，即系统达到同步状态的时间值依赖于系统的初始状态，这大大限制了其使用范围.尤其是对众多大型的网络系统，其初始状态往往很难测量或获得.因此如何确定收敛时间的上界，让网络同步的时间控制在给定的范围内便成为了一个比较重要且现实的问题.后来人们提出了固定时间同步的概念[3].例如，WANG L. M.等[4]研究了时滞非连续神经网络全局固定时间同步.CAO J. D.等[5]研究了时滞忆阻神经网络的固定时间同步,在Lyapunov稳定性理论的框架下，获得了主从忆阻神经网络固定时间同步的充分性条件，并估计出了收敛时间的具体上界.

另一方面，在实际应用中，网络节点之间既可能存在合作关系，也可能存在竞争关系，这样的网络被称为符号网络，对应的同步称为二分同步.目前对二分网络的同步研究已经取得一些成果.ZHAI S. D.等[6]研究了具有竞争关系及切换拓扑结构的耦合非线性系统二分同步.LIU F.等[7]研究了耦合时滞神经网络有限时间与固定时间二分同步.

文中将考虑激活函数为非连续的耦合时滞神经网络在外部干扰下的固定时间二分同步问题.基于固定时间稳定性理论，获得这类网络二分同步的充分性条件，并给出相应的仿真例子，模拟验证所得理论结果的正确性和有效性.

1 网络模型与预备知识

1.1 符号图

对于符号图G,如果存在2个集合Q1和Q2满足Q1∩Q2=∅,Q1∪Q2=Q,∀qi,qj∈Qk,k∈{1,2},aij≥0并且∀qi∈Qk,qj∈Ql,k≠l(k,l∈{1,2}),有aij≤0,那么称G为结构平衡图，否则称之为结构非平衡图.

引理1[8]对于结构平衡图,存在对角矩阵W=diag{w1,w2,…,wN}(wi∈{1,-1},∀i∈IN),使得矩阵WAW中的所有元素非负.

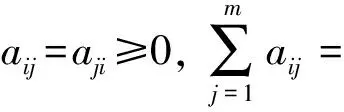
1.2 集值李导数

对于系统dx/dt=g(x),如果g(·)是非连续函数,那么g的Filippov集值映射定义为F(g(x))=∩δ>0∩μ(Ω)K[g(B(x,δ)Ω]，其中K(Φ)是集合Φ的凸包，并且B(x,δ)={y:‖y-x‖≤δ},μ(Ω)是集合Ω⊂Rn的Lebesgue测度.

令ΞU⊂Rn表示函数U(x)所有不可导的点的集合，则函数U的广义梯度∂U(x):Rn→B(Rn)定义为∂U(x)=co{limi→∞∇U(xi):xi→x,xi∉M∪ΞU}, 其中M⊂Rn是零测度集，co(·)表示凸包.

函数U(x)关于g在x处的集值李导数定义为LgU(x)={l∈R|∃φ∈F(g(x)),φTφ=l,∀φ∈∂U(x)}.

1.3 模型介绍

考虑一类由N个节点耦合而成的神经网络模型，其第i个节点(i=1,2,…,N)的动力学方程如下:

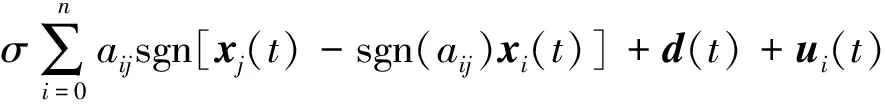
(1)

式中：xi(t)=(xi1(t),xi2(t),…,xin(t))T是t时刻第i个节点的状态向量；C=diag{c1,c2,…,cn}是n阶正定对角矩阵；H,B是n×n维的常数矩阵；f(xi(t))=(f(xi1(t)),f(xi2(t)),…,f(xin(t)))T,g(xi(t-τ))=(g(xi1(t-τ)),g(xi2(t-τ)),…,g(xin(t-τ)))T为神经网络激活函数，τ为网络时滞；J是神经网络的输入；σ是节点间的耦合强度；aij是节点i与节点j之间的连边，d(t)为有界外部干扰,满足‖d(t)‖≤d,d为正常数,ui(t)是待设计的控制协议.

耦合神经网络(1)的同步目标为

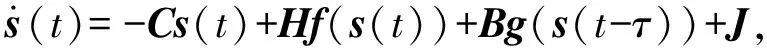
(2)

式中：s(t)=(s1(t),s2(t),…,sn(t))T∈Rn为同步目标轨道.

假设1函数f满足以下条件:

1) ∀x∈Rn,f(-x)=-f(x),g(-x)=-g(x);

2) 对于任意g(x)∈F[f(x)],g(y)∈F[f(y)],有sup‖g(x)-g(y)‖≤h1‖x-y‖+h2,其中h1,h2为正常数.

2 主要结论

本节将在结构平衡图与结构非平衡图下，分别讨论耦合神经网络(1)的固定时间二分同步问题.

首先，考虑在结构平衡图下，耦合神经网络(1)固定时间同步到目标网络(2).由引理1可知，存在对角矩阵W=diag{w1,w2,…,wN}(wi∈{-1,1}),使得WAW>0,且wiwjaij=|aij|,wiwj=sgn(aij),∀i,j∈IN.此时，耦合神经网络(1)实现固定时间二分同步是指存在给定时间T，使得当t→T时有xi(t)→wis(t), 且当t≥T时，xi(t)=wis(t).

令ei(t)=wixi(t)-s(t), 针对系统(1),文中设计控制器如下：

ui(t)=-k1sgn[wiei(t)]-k2sgnα[wiei(t)]-

k3[wiei(t-τ)],

(3)

式中：k1>0,k2>0,k3>0为控制增益；sgnα(x)=(sgnx)|x|α；α>1为幂参数.对∀i∈IN,令ηi(t)=wif(xi(t))-f(s(t)),ξi(t-τ)=wig(xi(t-τ))-g(s(t-τ)).

将控制器(3)代入网络系统(1)和(2),可得误差系统：

k1sgn[ei(t)]-k2sgnα[ei(t)]-k3ei(t-τ).

(4)

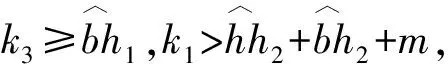
证明对于结构平衡图G, 由引理1可得

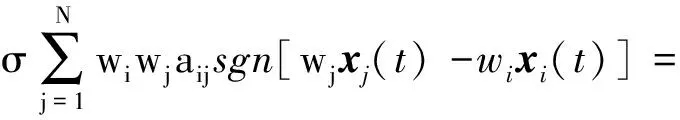
(5)

LδV1(t)=[∂V1(t)]·F[δ(t)]⊆

(6)

(7)

基于假设1, 可得

(8)

类似地, 有

(9)

将式(7)-(9)代入式(6)可得

(10)

进一步可得

(11)

下面对于φ正负性进行分类讨论.

情形1如果φ≥0，则

(12)

基于引理3及α>1,系统(1)在固定时间内达到二分同步，其收敛时间上界估计如下：

情形2如果φ<0，则

(13)

基于引理4，系统(1)可以在固定时间内达到二分同步，其收敛时间上界估计如下：

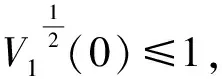
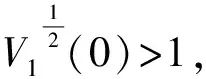
接下来,讨论结构非平衡图的情形,此时wi=0,即xi(t)→wis(t)=0.二分同步问题便退化为常规的稳定性问题.对此，设计如下控制器:

ui(t)=-k1sgn[xi(t)]-k2sgnα[xi(t)]-

k3[xi(t-τ)].

(14)

定理2若耦合时滞神经网络(1)在结构非平衡图下满足定理1的条件,则该网络在控制器(14)下达到固定时间稳定.

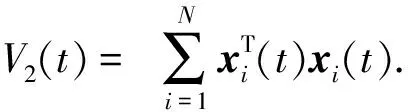
(15)

对于结构非平衡图，可知:

(sgnaij)xi(t)]=

(sgnaij)xi(t)]SIGN[xj(t)-(sgnaij)xi(t)]=

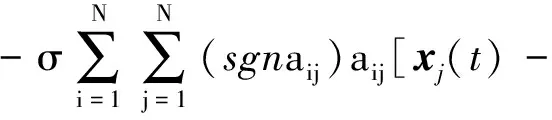
(sgnaij)xi(t)]SIGN[xj(t)-(sgnaij)xi(t)]=

(16)

将式(16)代入式(15)可得

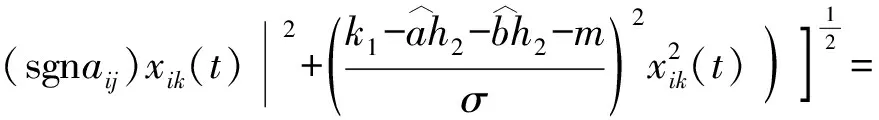
(17)

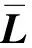
(18)

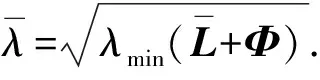
类似于定理1，下面根据φ的正负性进行讨论.

情形1如果φ≥0，则

基于引理4及α>1,系统(1)将在固定时间内达到稳定，其收敛时间上界估计如下：

由引理4可知，系统(1)将在固定时间内达到稳定，其收敛时间上界估计如下：

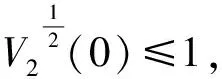
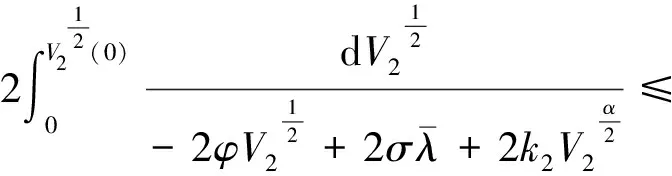
需要指出的是：文献[7]考虑了耦合神经网络的二分同步问题，文中则将文献[7]中的连续激活函数推广至非连续的情形，并进一步考虑了耦合网络在外部干扰下的固定时间同步问题，结论更具有一般性.

3 数值仿真

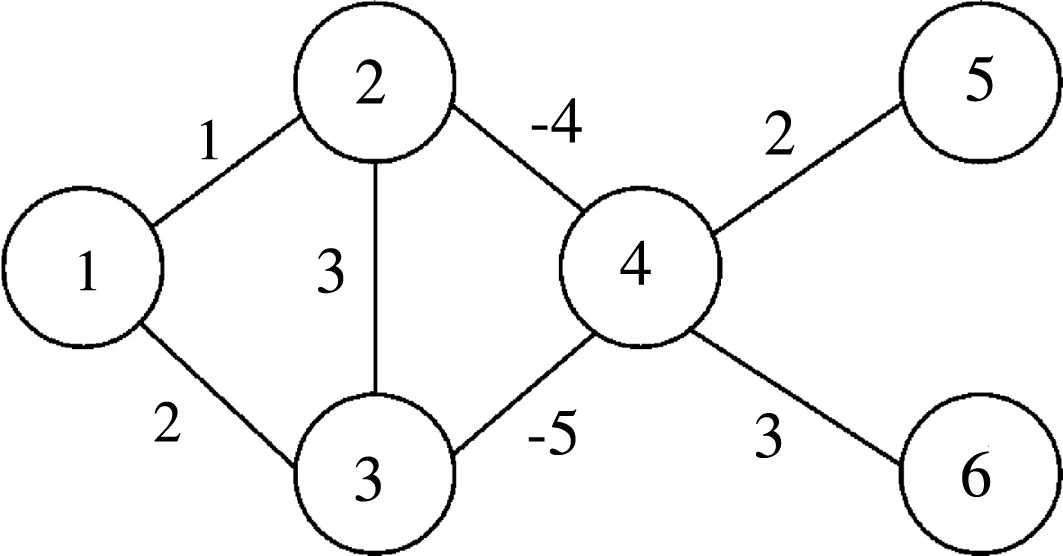
图1 结构平衡图

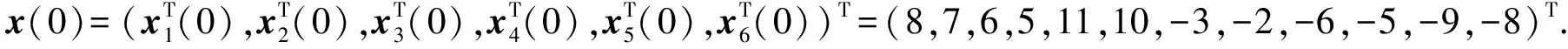
图2 结构平衡图下的固定时间二分同步

例2考虑耦合神经网络(1)在结构非平衡图(见图3)下的固定时间稳定问题，节点初始状态为x(0)=(4,3,5,4,-3,-2,-1,0,-6,-5,9,8)T,其他条件与例1相同.由定理2可知，耦合神经网络(1)在结构非平衡图下达到固定时间稳定,其收敛时间上界T2=0.239，仿真结果如图4所示.

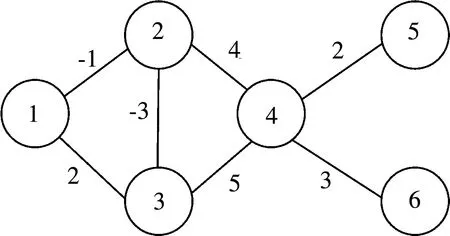
图3 结构非平衡图

图4 结构非平衡图下的固定时间稳定

4 结 论

文中主要研究了具有外部干扰的耦合时滞神经网络固定时间二分同步问题.基于Lyapunov稳定性理论，通过设计适当的控制协议确保了具有非连续激活函数的耦合神经网络在结构平衡图与结构非平衡图下均能够实现固定时间内达到二分同步，并分别给出了相应的收敛时间上界.最后通过一些仿真实例验证了所设计算法的有效性及理论结果的正确性.