计算机扑克智能博弈研究综述

袁唯淋，廖志勇，高巍，魏婷婷，罗俊仁，张万鹏，陈璟

计算机扑克智能博弈研究综述

袁唯淋，廖志勇，高巍，魏婷婷，罗俊仁，张万鹏，陈璟

（国防科技大学智能科学学院，湖南 长沙 410073）

计算机博弈是人工智能领域的“果蝇”，备受人工智能领域研究者的关注，已然成为研究认知智能的有利平台。扑克类博弈对抗问题可建模成边界确定、规则固定的不完美信息动态博弈，计算机扑克AI需要具备不完全信息动态决策、对手误导欺诈行为识别以及多回合筹码和风险管理等能力。首先梳理了以德州扑克为代表的计算机扑克智能博弈的发展历程，其次针对计算机扑克智能博弈典型模型算法、关键技术以及存在的主要问题进行了综述分析，最后探讨了计算机扑克智能博弈的未来发展趋势和应用前景。

计算机扑克；认知智能；不完美信息博弈；德州扑克；虚拟遗憾最小化

1 引言

随着人工智能技术的不断发展进步，人工智能领域的研究正从计算智能与感知智能逐步走向认知智能，面向认知智能的“智能博弈”主题备受关注。近十年来，认知智能结合大数据、云计算等颠覆性技术不断向各领域渗透，加速推动人工智能真正转变为现实的生产力。计算机博弈（computer game）是人工智能领域的“果蝇”，人机对抗是衡量认知智能水平的重要途径，被广泛地用来作为计算机智能发展水平的测评基准和里程碑[1]。从早期的国际象棋，到近几年面向围棋[2-3]、德州扑克（TH，Texas Hold'em）[4-8]等回合制棋牌游戏以及即时策略游戏[9-10]的人工智能的设计，每一次技术上的突破都在各界产生强烈反响，由此产生的成功更是人工智能发展史上的重要里程碑。继人工智能攻克围棋之后，美国卡内基梅隆大学（SMU）在Science上公布了令人瞩目的研究成果[4]：德州扑克程序Pluribus在多人无限注德州扑克中战胜了人类专业选手，极大地震撼了学术界和社会各界。

在德州扑克问题上取得的进展，不仅意味着在不完全信息动态博弈技术上的突破，更多的是认知智能博弈发展取得的新成就和技术高度。智能博弈技术的成熟与应用，将会进一步扩展智能博弈的应用边界从金融[11]、医疗健康、安全等领域，向战略性资产组合、自动驾驶策略等方面渗透，未来应用前景广阔，研究意义重大。计算机扑克的研究与许多现实问题（如网络安全和国家防御）也极为相关，对于现实世界的交互，包括反欺诈、网络安全[12]和内容审核等，涉及隐藏信息的场景都能通过不完全信息博弈理论方法建模。

本文着眼于智能化时代的认知智能需求，介绍以德州扑克为代表的计算机扑克智能博弈的发展历程, 就计算机扑克智能博弈典型模型算法、关键技术以及存在的主要问题进行了综述分析，并探讨基于博弈理论的认知智能新方向的未来发展趋势和应用前景。主要贡献如下：①介绍了计算机扑克智能博弈的发展历史与现状；②对计算机扑克进行复杂度分析；③针对计算机扑克智能博弈中涉及的对手建模、近似均衡策略求解和非近似均衡求解等关键技术进行介绍，并分析其优缺点；④分析了智能博弈的研究趋势和应用前景;⑤对计算机扑克智能博弈做出总结展望。

2 计算机扑克智能博弈发展历史与现状

不完美信息博弈（IIG， imperfect information game）自20世纪90年代成为人工智能领域的研究热点，而以德州扑克为代表的计算机扑克智能博弈，由于其规则确定、游戏环境可控和信息不完全等特点，一直是不完美信息博弈问题中具有吸引力和挑战性的难题。

在驱动计算机扑克智能博弈研究发展的力量中，加拿大阿尔伯塔大学（UA）、美国卡内基梅隆大学等具有突出贡献。本文对近几年国内外的计算机扑克智能博弈相关研究工作按不同组织机构进行了归纳总结（如表1所示）[13-24]，分析各组织研究路线的异同，为未来计算机扑克智能博弈的发展提供思路，其中，M-L表示多人有限注德州扑克，2-L表示两人有限注德州扑克，2-NL表示两人无限注德州扑克。

2.1 阿尔伯塔大学研究组

加拿大阿尔伯塔大学计算机扑克研究组UACPRG使用基于规则的方法开发出第一个扑克程序，根据给定的博弈状态，输出特定的动作，能够击败较弱玩家。此后，扑克程序中陆续出现了对手建模和神经网络建模等技术，计算机博弈水平显著提高。2003年，Billings等针对两人有限注德州扑克问题，提出了最优策略理论[25]，虽然没有考虑对手的相关信息，但构建的智能体表现出了较高的博弈水平。2006年，Sturtevant等进一步深入研究两人有限注德州扑克问题，将对手建模与博弈树搜索技术相结合，在合理的时间内实现深度优先搜索[26]。2007年，基于纳什均衡的著名扑克AI程序Polaris在人机对战的扑克冠军赛中击败了人类选手[27]，又在当年的世界年度扑克机器博弈大赛（ACPC）中夺冠，为扑克研究带来了新的突破。传统上，线性规划是解决扩展式博弈（extensive game）的先进技术之一，但线性规划难以应对指数级状态数量的博弈。2007年，Zinkevich等提出虚拟遗憾最小化（CFR，counterfactual regret minimization）算法[28]，这是一种迭代算法，将整体最小遗憾值分解到各个独立的信息集（information set）中计算局部最小遗憾值，能成功解决多达1012个状态的博弈问题。并且，在（信息集数量）大规模的两人零和博弈中，使用该方法收敛到纳什均衡解具有理论保证。随后，Risk将CFR算法应用到扑克智能体上[29]，并以显著性的优势赢得了ACPC三人有限注德州扑克比赛的冠军。2015年，Bowling等改进基础CFR，提出新变体CFR+算法[30]，并应用其开发的程序“仙王座”（Cepheus）首次破解了两人有限注德州扑克（HULTH，heads-up limit Texas Hold’em）（以下简写为HUL）的决胜方法，Cepheus从每一局的概率上来说还是会输，但从长远来看可以取得统计学上显著的胜利。2017年，一种新型的扑克AI程序DeepStack[5]被设计出，在两人无限注德州扑克（HUNLTH，Heads-Up No-Limit Texas Hold'em）（以下简写为HUNL）上击败职业扑克玩家。DeepStack结合了递归推理来处理不对称性信息，利用持续求解技术将计算集中到相关的决策上，并设计深度神经网络拟合遗憾值，这是一种可用于非完美信息扩展博弈的通用算法。2019年5月，可利用性下降新算法[31]被提出，通过针对最坏情况对手的直接策略优化，计算两人零和不完美信息扩展博弈中的近似均衡。当遵循这种优化时，玩家策略的可利用性渐近地收敛为零，因此当两个参与者都采用这种优化时，联合策略会收敛到纳什均衡。与虚拟自博弈（fictitious self-play）和CFR不同，该收敛结果与优化的策略有关，而不是平均策略。

表1 德州扑克AI相关工作总结

总体来说，UACPRG组织最早关注于计算机扑克智能博弈研究，输出了大批学术与应用成果，形成了以“仙王座”、DeepStack为代表的顶尖AI，不断刷新博弈对抗记录，拉开了新一轮人机大战的序幕。

2.2 卡内基梅隆大学研究组

除了UACPRG团队，近年来国际上出现了一些研究智能博弈的组织和个人，在攻克德州扑克的新型图灵测试中成果丰硕。其中，美国卡内基梅隆大学的研究引人瞩目。2017年，与DeepStack同时，Noam等针对德州扑克的不完美信息博弈的特点，提出了一种在理论上和实践上都超越了之前方法的子博弈求解技术，研发的德州扑克AI程序“冷扑大师”（Libratus）[6]在HUNL中击败人类顶尖职业玩家，引起学术界和社会各界的轰动。Libratus的核心突破在于嵌套求解（nested solving）技术，随着在博弈树的位置不断下移，Libratus能实时调整计算更加精细的策略。2018年，Brown提出了一种在不完美信息博弈中进行有限深度优先搜索的方法[32]，允许对手在深度有限情况下为其余部分选择多种策略，并仅使用计算机上的计算资源（一块4 核的CPU和16 GB的内存）生成大师级的HUNL扑克AI：Modicum，击败了两个以前版本的顶级德州扑克AI。2019年2月，Noam又提出了基于神经网络的CFR变体DCFR[33]，用神经网络拟合累计遗憾值和平均策略，打破表格式CFR的局限性，为大规模不完全信息动态博弈提供了新的解决思路。2019年7月，Noam在Science上发表的多人德州扑克最新研究成果备受瞩目——多人无限注德州扑克AI程序Pluribus[6]在六人无限注德州扑克中战胜了人类专业选手。该算法的核心是采用自博弈的方法不断学习和调整策略，并提高胜率，类似于AlphaGo Zero，不需要任何的人类先验知识。虽然能够击败人类顶尖玩家，证明了Pluribus的实用性，但不同于Libratus和DeepStack，Pluribus在解决多人博弈问题上仍缺乏理论支撑。

2.3 其他组织研究进展

除此之外，机器学习、最优化理论、决策论等领域的方法和观点被不断引入不完全信息博弈领域，并取得了较大的进展。Passos等在德州扑克中应用强化学习算法[34]，并结合特定的对手模型，取得了不错的效果。Zhang等结合MCTS和神经虚拟自博弈（NFSP，neural fictitious self play），提出了异步神经虚拟自博弈（ANFSP）方法[35]，提升了在大规模不完全信息零和博弈上的表现。ANFSP让AI程序学会在多个仿真环境中进行“自我博弈”，从而生成最优策略，该方法在德州扑克和多人FPS射击游戏中均取得了不错表现。哈尔滨工业大学较早开始对德州扑克展开研究。2013年，该团队利用手牌评估和对手建模方法构建的德州扑克AI程序，在ACPC大赛的HUL项目中位列第四名[36]；2014年，该团队利用基于人工神经网络和风险占优策略构建的扑克AI在ACPC大赛3人Kuhn扑克项目取得第三名[37]。2016年，采用CFR算法开发的系统获得ACPC大赛的HUNL项目排名第8名[38]。国内研究起步晚于国外，但发展迅速，不断推动智能博弈的发展。本文对比了国内外近几年的高水平两人无限注德州扑克，其智能水平总结对比如图1所示。

2.4 典型计算机扑克AI程序介绍

对于扑克这类信息集数量大规模的博弈，CFR算法是目前最先进的能够生成高效策略的技术之一。下面介绍CFR算法在德州扑克领域具有代表性的成就。

（1）Cepheus

Cepheus首次破解了HUL[17]问题，具有所需计算量少、适合大规模并行化等特点。基础的CFR算法及其一些变体，在处理大规模博弈上会面临两个挑战：内存和计算。Cepheus采用定点计算和压缩的方式解决存储问题，结合剪枝和省略对平均策略的计算突破CFR算法在计算规模上的限制；跳过计算和存储平均策略的步骤，使用玩家的当前策略作为CFR+的解；CFR通常只对博弈树的一部分进行采样，以便在每次迭代时进行更新。CFR在每个信息集上使用遗憾匹配的变体（regret matching+），其遗憾值被限制为非负数。表现“差”的动作在被证明有用之后，将被立即再次选中（而不是等待多轮迭代后其遗憾值变成正值）。从每一局的概率上来说虽然还是会输，但从长远来看可以取得统计学上显著的胜利。CFR+算法在较弱意义上破解了HULTH，这是不完美信息博弈中的里程碑事件。

（2）DeepStack

DeepStack[5]通用算法使用了深度学习自我玩牌，学习策略战胜人类玩家。DeepStack使用神经网络拟合评估函数、近似反事实后悔值。该深度反事实价值网络（deep counterfactual value network）以当前迭代的公开状态和范围、池底大小等手牌簇作为输入，特征经过7层全连接的隐藏层输出后归一化处理，从而保证该值满足零和约束，最后映射为两个玩家的反事实后悔值。在比赛之前，通过生成随机扑克场景（底池大小、台面上的牌和范围）来训练深度反事实价值网络。该方法在理论上有两人零和博弈的收敛性证明作为支撑，并且在实践中能得出比之前的方法更低的可利用性。

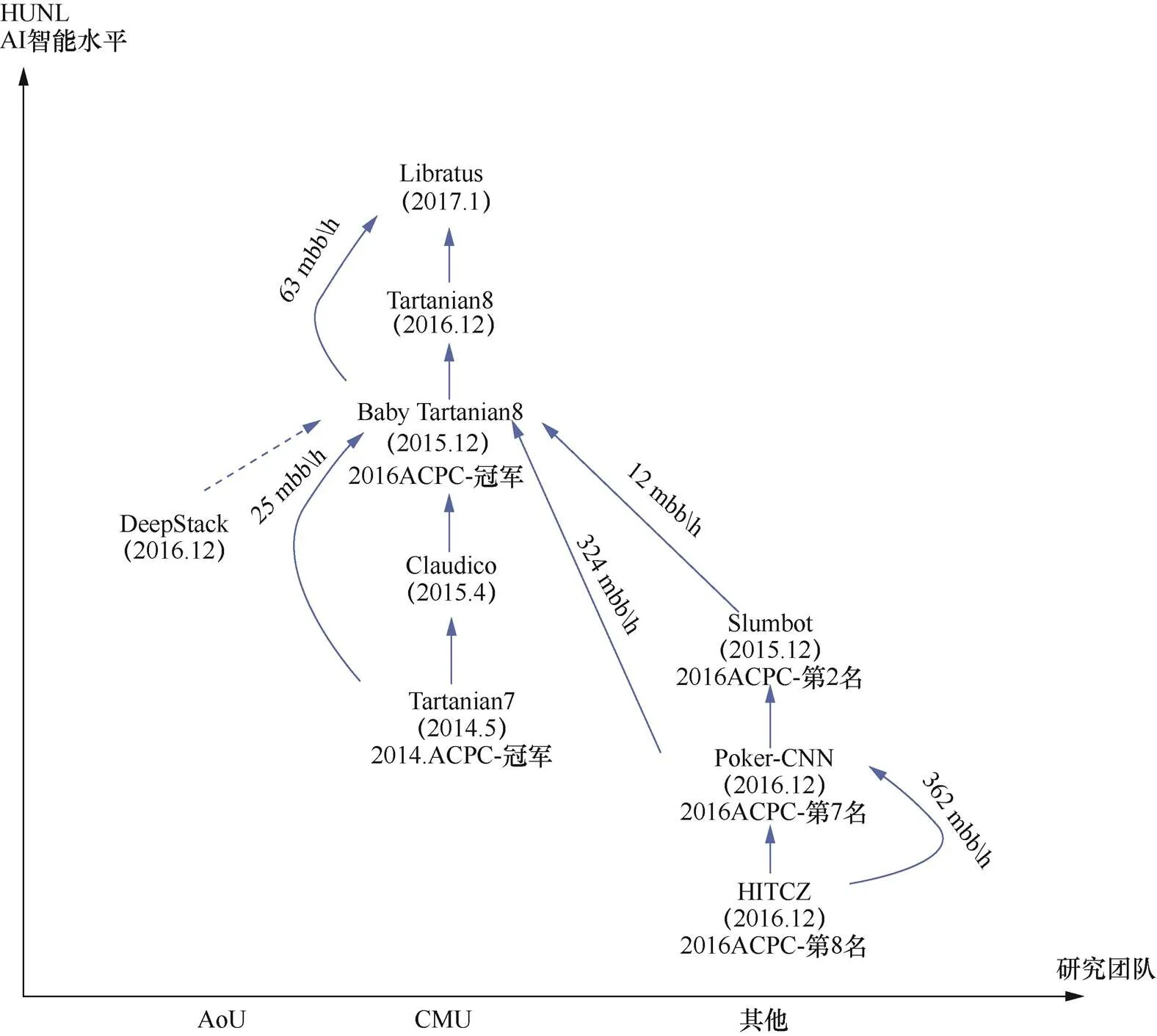
图1 HUNL中AI智能水平对比

Figure 1 AI level in HUNL

（3）Libratus

2017年，美国卡内基梅隆大学开发的扑克AI“冷扑大师”[6]在与4名人类顶尖选手之间的“人机大战”中取得胜利，这是人工智能第一次在HUNL中击败顶尖的人类玩家。Libratus主要由3个主要模块组成。

第一模块，预先对博弈进行动作抽象和手牌抽象，计算蓝图策略。直接对HUNL的不同决策点计算策略不可行。Libratus首先针对大规模博弈树进行抽象压缩，然后使用了CFR的变体MCCFR算法来计算蓝图策略。同时，Libratus通过一种基于遗憾值修剪法的采样方式改进了MCCFR，允许修剪掉在博弈树中“失败”的分支，以便加快MCCFR算法的收敛。

第二模块，是嵌套子博弈求解算法，基于构建的更细粒度的抽象进行实时求解，求解子博弈的目的是在子博弈中改变策略来提升蓝图策略。与完美信息博弈中的子博弈求解技术不同，在不完美信息博弈中子博弈求解方面存在一个主要挑战：一个玩家在子博弈中的最优策略可能依赖于博弈其他部分的策略和结果。因此，不能只用子博弈的信息来解决子博弈。现有的使用实时子博弈求解方案需要假定对手按照蓝图策略进行博弈来解决这个问题。然而，对手可以通过简单地切换到不同的策略来利用这个基本假设。所以，该技术也被称之为“不安全”的子博弈求解。不安全的子博弈解决缺乏理论上的求解质量保证，而且在很多情况下，效果不佳，因为不安全子博弈求解技术无法确保得到策略的可利用性一定比蓝图策略低。Libratus利用安全子博弈求解技术确保了策略的可利用性不高于蓝图策略，保证了无论对手使用何种策略，Libratus都能通过确保子博弈策略符合原始抽象的蓝图策略来实现这一点。

第三模块，是一个自我改进模块，随着时间的推移不断改进蓝图策略，利用所发现的对手策略中的潜在漏洞部分，计算出更接近纳什均衡的策略。

（4）Pluribus

2019年7月，Pluribus[4]在六人桌比赛中，对战5名顶尖人类选手并取得了胜利。Pluribus系统是在Libratus的基础上改进的。但与Libratus系统不同之处有以下3点。

① Pluribus的目标不是一个具体的博弈论概念，而是从实验层面解决多人扑克问题。Pluribus的成功表明，尽管它在对多人游戏中缺乏已知的强有力的理论保证，但在多人大规模不完全信息博弈问题中，通过精心构造自博弈搜索算法仍然可以产生较好的策略，战胜人类玩家。

②Pluribus采用全新的在线搜索方法，通过搜索前面的几个博弈路径，来评估自己下一步可选的策略。在完全信息博弈中，包括双陆棋、国际象棋和围棋，实时搜索对于获得超过人类的性能是必不可少的。因此，Pluribus在与对手的实际比赛中，采取了不完全信息博弈中的深度限制搜索，通过实时搜索在比赛中发现更好的策略。将自博弈形式与搜索形式相结合，已经在完全信息下的两人零和博弈中取得了巨大的成功。对于涉及隐藏信息和两个以上玩家的情况，使这一问题在理论和实践上有很大的不同和显著的困难。

③ Pluribus具有更快的自我博弈算法。在线搜索算法和自我博弈算法的更新与结合，使Pluribus能用比Libratus更少的处理能力和内存来进行训练。Pluribus策略的核心是通过自博弈来计算的。在自博弈中，AI对自己的副本进行博弈，而不需要任何人类或先前的人工智能博弈的数据作为输入。从零开始随机采取动作，并随着确定是哪些动作以及这些动作的概率分布而逐渐改进，从而相对于早期版本的策略产生更好的结果。Pluribus改进MCCFR进行自博弈，通过自博弈为整个离线博弈生成蓝图策略。人工智能从完全随机对抗开始，通过学习击败自己的早期版本而逐渐改进。抽象后的博弈求解得到的蓝图策略必然是粗粒度的。当决策点的数量足够少时，Pluribus会进行实时搜索，以确定针对当前情况更好、更细粒度的策略。

3 计算机扑克复杂度分析

博弈的复杂度反映了对应AI程序设计的难度，但并不完全等价，难度也取决于不同的战术、团队配合等因素。博弈的状态空间复杂度是指从博弈初始状态开始，可以到达的所有符合规则状态的总数。不完全信息博弈中，博弈问题的复杂度可以根据博弈状态数量、信息集的数量和每个信息集下合法动作的数量进行分析[17]。与围棋不同，扑克由于对手手牌信息的私有性导致牌局信息不完全可知，求解空间复杂，难以搜寻均衡解。本节以德州扑克为例，分析计算机扑克智能博弈的复杂度。

3.1 德州扑克

德州扑克是一种不完美信息不确定性动态博弈，与桥牌等大多数计算机扑克智能博弈问题相似，是继围棋之后受关注的人工智能领域难题之一[39-40]。这里先简要介绍德州扑克中的术语。区别于传统的机器博弈研究，按照下注的限制分为无限注（No-Limit）和有限注（Limit）德州扑克，一般由2到9人参加，使用52张扑克牌，游戏分为4个阶段：翻牌前、翻牌、转牌、河牌。每个玩家在翻牌前阶段发两张私有的“底牌”，仅玩家自己可见。在下注之前，在庄家左边的两个位置玩家必须分别强制投注小盲注和大盲注，大盲注是小盲注的两倍，并通常用每手所赢的大盲注的倍数，即平均赢率来评价玩家的水平。然后剩余玩家通过弃牌、跟注或加注开始下注，共计三轮下注。每轮下注后分别发出3张、1张和1张，共计5张公共牌，玩家通过下注过程之后，由手上的2张牌和5张公共牌组合，场上所有未弃牌的玩家持大的牌型者获胜。牌型按牌力由大到小分为皇家同花顺、同花顺、四条、葫芦、同花、顺子、三条、两对、一对和高牌。

3.2 状态数

表2 HUNL各阶段状态数

每个阶段的下注动作（包括弃牌、跟注和加注）独立于可能的状态数，因此加注的区间决定了两人德州扑克博弈树的“宽度”，影响着下一阶段的状态数。由于德州扑克玩家无论持有什么样的底牌，可以选择的行为组合相同，所以在计算状态空间复杂度时，可以用可能的底牌组合数与可选择行为数相乘，状态空间约为3.162×1017。

3.3 信息集数量

假设每阶段只允许加注4次，在枚举可继续到下一阶段的动作序列时，玩家不弃牌。“-，r，c，f”分别代表该阶段首次决策、加注、跟注和弃牌，则翻牌前，决策点有“-，c，cr，crr，crrr，r，rr，rrr”，共8个，可以进行到下一阶段的动作连续系列为“cc，crc，crrc，crrrc，rc， rrc，rrrc”，共7个，终止在该阶段的序列为“f，rf，rrf，rrrf，crf，crrf，crrrf”，共7个，以此类推可得各阶段的序列个数[41]如表3所示。则整个博弈树上的信息集数量为

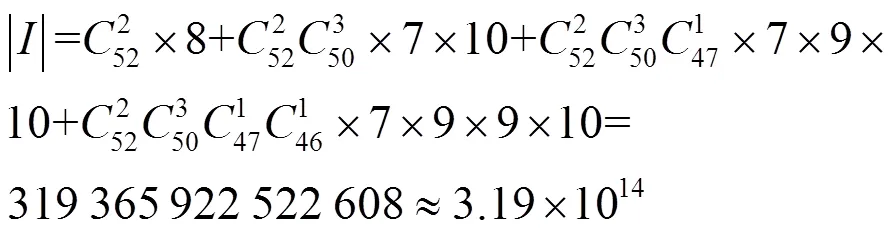
表3 HUNL各阶段序列数

3.4 信息集下动作数量

4 计算机扑克智能博弈关键技术

德州扑克这类不完全信息博弈问题的求解方法一直在创新发展中。其中，对手建模[42]的方法最早被应用于德州扑克程序的开发，随后基于强化学习、深度学习和贝叶斯网络等模型相继被提出。迄今为止，基于博弈均衡策略的德州扑克智能博弈求解方法取得较大突破，现存的顶尖AI程序大多基于博弈论的框架开发，并结合抽象、子博弈求解和均衡策略搜索等方法快速求解近似均衡策略。本节详细介绍德州扑克智能博弈中涉及的关键技术（如图2所示）。

4.1 对手建模与利用

博弈论一般研究对称条件下两人零和博弈问题，是各自利用对方的策略调整自己的对抗策略，达到取胜的目的。博弈论考虑博弈局中人的预测行为和实际行为，并研究其对应优化策略。对手建模是在对抗环境下，考虑如何对除自己以外其他参与者进行行为建模，这是一种典型的行为预测技术[43-44]。多智能学习领域对手建模主要有以下几种方法[45]：策略重构、类型推理、行为分类、行为识别、递归推理、图模型、群组建模、集群建模。按照建模方式，既有由更新博弈树节点上的对手概率分布，推导出对手的典型模型，得到最优的对应策略的显示建模方法；又有直接根据对手历史数据和公共信息直接生成响应策略的隐式建模方法。

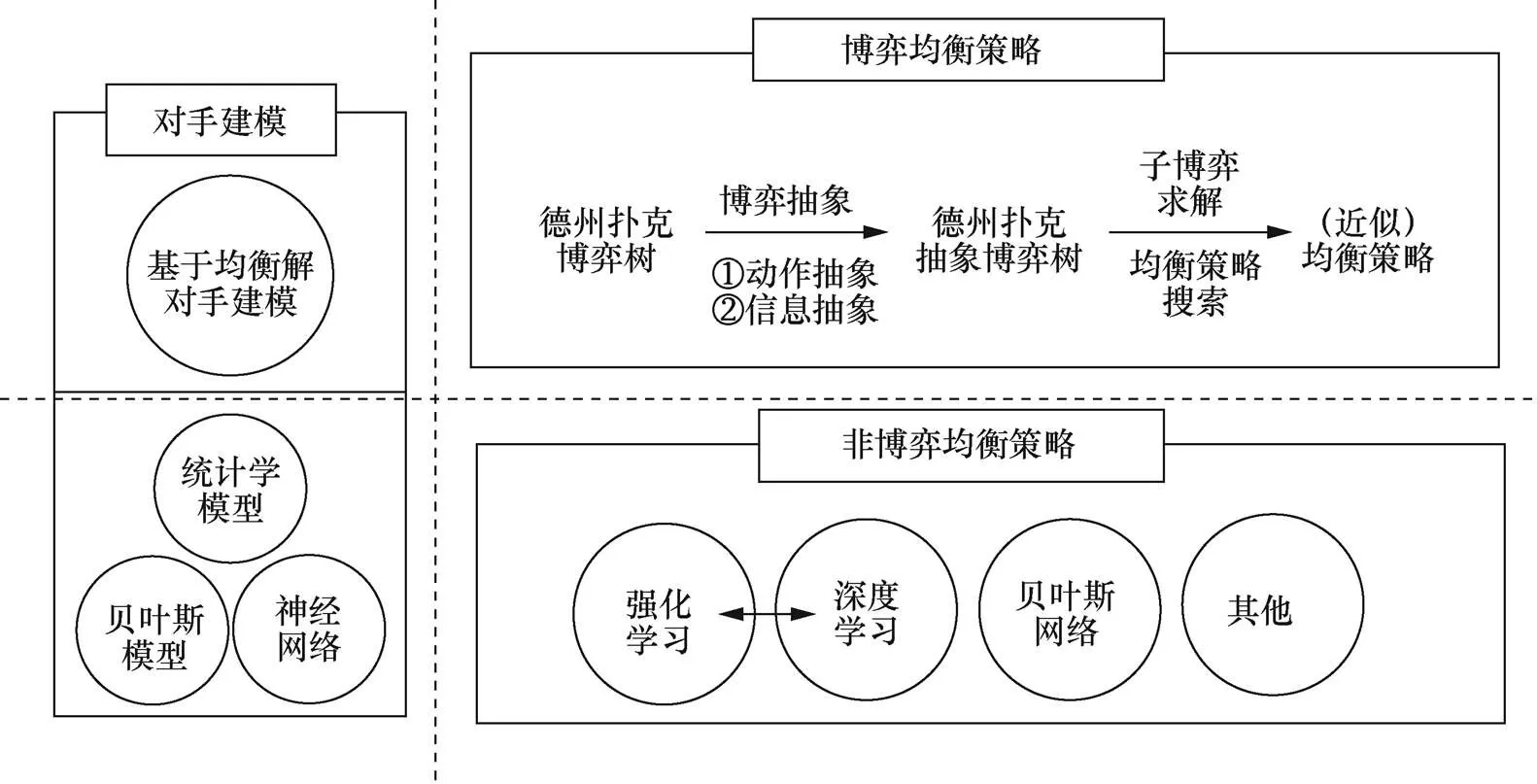
图2 计算机扑克智能博弈中的关键技术

Figure 2 The key technology of intelligent game of computer poker

在不完美信息博弈中，博弈状态存在一些不确定因素，如在德州扑克游戏中对手的手牌信息以及博弈后续阶段的公共牌信息。因此，博弈者要对整个博弈局面进行评估往往是很困难的，这往往导致博弈者在决策时做出错误的选择，而在一次博弈中，任何一个错误的策略都可能会导致博弈的失败。因此，对于博弈中存在的不确定因素，最好的处理方式就是将其转化为已知条件，但这通常难以完成。例如，德州扑克在博弈过程中，要想确定对手的手牌是一件不可能的事情。然而，就一般的计算机博弈而言，所有玩家的策略一般是有限的，通过学习对手在不同博弈状态下策略的偏向来预测对手在当前博弈状态下会做出的策略，这对博弈者来说是可以做到的，而且这些预测信息能为博弈者提供一个很好的博弈信息，方便博弈者做出更好的决策，甚至可以通过对手的动作序列以及历史数据来推测当前博弈状态下的优劣情况。例如在德州扑克中，可以通过对手的动作序列以及历史数据来预测对手下一步的动作以及对手的手牌强度。

在纳什均衡解概念中，双方都采用均衡策略，任何偏离均衡策略的一方所获得的收益将减小。对于非完全理性的对手，其策略和纳什均衡策略之间的“距离”，为其他均衡策略玩家创造了可利用性。在求解（近似）纳什均衡解时，可利用度是均衡策略质量的衡量标准，指该策略在预期中相对最坏情况下对手策略所达到的少于博弈价值的量。通常将这个差值称为一个策略的可利用度。可利用度衡量了对手从玩家未采用纳什均衡策略中获利的程度，即因玩家偏离纳什均衡策略，对手用强有力的应对策略对其做出惩罚的程度。这是对策略最坏情况下质量的度量，使可利用度成为在不知对手如何采取策略的前提下评估任何算法和技术的天然指标。

对手建模是德州扑克智能博弈中一个重要方向，研究如何建立一个清晰的模型来预测对手的行为。对手建模研究内容分为两部分：手牌范围建模和行为习惯建模。前者研究的是选手会手持什么样的牌入局；后者研究的是入局后在不同情况下会采取何种行动。

4.1.1 基于非均衡解的对手建模方法

本小节概述了对手建模和相关AI开发的早期工作。目前，基于非均衡解的对手建模主要包括基于规则的统计学模型、贝叶斯模型以及神经网络模型。

（1）基于规则的统计学模型

基于规则的统计模型是构建自适应扑克智能体过程中的早期探索。最初，Billings构建的扑克程序Loki[13]，能够通过观察其对手构建的对手模型，并动态调整博弈方式以利用对手的类型、模式和性格。Loki通过权衡可能的对手手牌来建模对手，手牌的权重根据对手的动作，通过手工设计的规则进行初始化和调整。

随后，Billing采用了特定的对手模型并为每个对手构建了统计模型，提出了基于规则的扑克智能体Poki[14]，特定模型有针对性地利用对手的弱点，效果明显优于通用模型。2006年，Billings提出了基于自适应博弈树算法的对手模型——Miximax和Miximix。该算法将不完美信息博弈树的决策节点建模为具有概率的机会节点，从而计算出期望值。该算法对不完美信息博弈的叶节点执行全深度优先搜索，以计算每个动作的期望值。对手在每个决策节点上可能采取的行动的概率近似为过去行动的频率计数。摊牌节点上的期望值是使用对手牌力的概率密度函数估算的。

（2）贝叶斯模型

基于贝叶斯模型的对手建模依赖于对手的先验知识。早期的通用贝叶斯概率模型模拟了博弈动力学和对手策略，基于后验分布考虑了近似贝叶斯最佳响应、最大后验概率和汤普森响应等计算最佳响应的方法，适用于多变体扑克。文献[46]在Leduc扑克和有限注德州扑克上使用了独立的Dirichlet先验和专家定义的知情先验。实验表明，通用贝叶斯概率模型能够在前期快速捕获对手策略，并且随后的响应能够快速利用对手。之后出现的方法着重学习适应特定对手的先验（即对手行为的期望）和关系回归树，以达到快速预测人类玩家在比赛中的动作和结果的目的。

（3）神经网络模型

基于人工神经网络的对手建模方法，是人工智能领域中最简单有效且不需要过多相关领域知识的方法。计算机扑克中，神经网络可以用来预测对手行为，并以此提供辅助决策信息。神经网络可以用于构建对手模型或直接训练扑克智能体，并且神经网络预测器的性能通常优于简单的统计模型。但考虑对手模型的神经网络预测器的性能优于不考虑对手模型的情况，构建神经网络模型预测在HUL中对手的动作时，采用表示博弈状态的概率的元组作为神经网络的输入，通常可以实现准确性较高的预测。

然而，神经网络在实际的计算机扑克博弈中并不适用于对手建模。在实际对弈中，不管对手采用哪种类型下的策略，所有的决策都会依靠其当前手牌牌力，但对手的私有手牌是不可观的。

4.1.2 基于均衡解的对手建模方法

纳什均衡近似方法已成为近年来构建HUNL智能体的主流方法，但缺乏建模对手和利用对手的能力。因此，对手建模和均衡近似结合起来成为一种新思路。Ganzfried提出了一种高效的实时算法[47]，该算法在观察对手动作频率的基础上，将近似均衡策略与观察量相结合来构建对手模型，根据对手模型计算并实行最佳响应，不断进行实时更新。这种方法结合了博弈理论和对手建模，仅需很少的交互就可以有效地利用对手。但是，用这种方法构建的智能体可能会被强大的对手充分利用，进行对抗攻击。Norris引入了一个统计利用模块[48]，该模块能够将对手利用添加到任何HUNL的基本策略中。该模块旨在识别对手比赛中的统计异常，并通过使用专家设计的统计利用方法有针对性地利用这些异常，确保了模块的添加不会使基本策略更具有可利用性。Ganzfried提出了安全策略的完整特征[49]，并提出了有效算法以利用次优对手保证策略安全。

4.2 博弈建模与博弈策略求解

与完全信息博弈不同，不完全信息博弈难以分解为可独立求解的子博弈问题，因为不完全信息博弈分解得到的子博弈的最优策略可能依赖于其他子博弈的策略与输出。德州扑克状态空间过于庞大，无法遍历所有的状态以寻求最优解。通常采用抽象的方法，对此类状态空间庞大的博弈进行求解。对于不完全信息博弈领域问题的求解，通常将问题抽象简化为相对简单的问题，得到一个简化解，之后通过增加约束，逐渐逼近完全信息博弈所对应抽象问题的解[50]。目前，已有的比赛用扑克AI程序往往使用抽象算法，生成更小的博弈，之后使用自定义均衡搜索算法来解决抽象出来的博弈问题。德州扑克，由于其状态空间过于庞大，不可能将所有的状态遍历求最优解。为此，通过抽象的方法对德州扑克的博弈模型进行简化求解。通常简化求解过程分为以下3步[50]，如图3所示。

①在保留原始模型策略结构的前提下，将其抽象为较小的博弈模型。

②通过迭代算法（如CFR）求解较小博弈模型的近似纳什均衡解。

③将求得的纳什均衡解映射到原始博弈空间中。

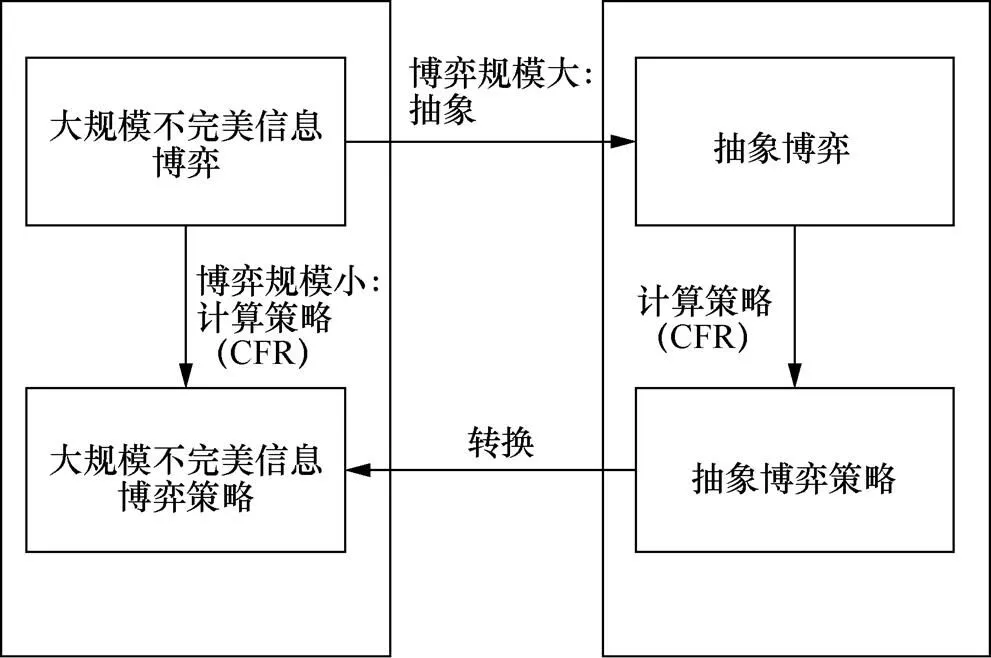
图3 博弈模型的抽象

Figure 3 Abstraction of game model

4.2.1 博弈问题抽象

抽象算法能对当前的博弈进行描述，产生一个更小但策略上相似的博弈，甚至产生完全类似的抽象博弈。常见的抽象技术包括动作抽象和信息抽象[51-52]。

动作抽象：在一些大型或无限动作空间的博弈中，由于动作行为的复杂性，博弈求解难度大大增加。此时，有效的动作抽象有助于减少搜索、降低问题的复杂度。例如，在德州扑克中，在100元大盲注设置下，下注2 000～2 999美元的行为差别不大。在动作抽象的过程中，可以将差距较小的动作抽象为同一动作，以此将动作空间离散化。动作抽象存在的问题是，玩家会执行一些在已抽象模型外的动作。针对这一情况，需要定义一个动作映射函数，将动作映射到建模好的动作抽象上，相关的映射方法如随机算法映射、确定性几何映射、随机几何映射和伪谐波映射等，但对离线决策没有较大影响。

信息抽象：信息抽象是将相似状态信息合并为相同的类或桶。根据对状态的抽象程度，信息抽象分为无损信息抽象和有损信息抽象。常见的无损信息抽象算法，如GameShrink算法[53]，是一个自下而上的动态算法，可以合并所有有序博弈的同构节点。GameShrink存在抽象不准确，无法确定抽象类数量，以及计算量大等问题，文献[54]针对这些问题，对GameShrink进行了优化。当抽象层次较高时，会发生信息丢失。求解该抽象问题的方法是使用有损信息抽象算法，如GameShrink算法的有损版本。有损信息抽象对无损信息抽象的有序同构节点进行了扩展。扩展方式包括将兄弟节点的子节点视为有序同构节点。总之，信息抽象依赖相似信息；如果节点之间的相似度高，将大幅减少搜索空间；如果相似度定义不准确，也会导致不良的结果。Noam等在2014年ACPC比赛中，使用了有损抽象，借助分层抽象以及MCCFR算法，在HUNL中，取得了显著的成绩[55]。

4.2.2 基于子博弈的策略求解

在不完全信息博弈中，求解子博弈的过程被定义为近似解逼近过程，或通过求解不相交的子博弈来改进当前的结果[56]。在完全信息中，可将博弈分解为独立的子博弈以求解。但在不完全信息博弈中，因为子博弈的最佳策略可能取决于其他未知子博弈的策略和输出，所以完全信息博弈中的分解方法不适用。因此必须在传统子博弈技术的基础上加以改进。以下是针对不完全信息博弈的改进子博弈的解决方案。

（1）非安全子博弈解

最直观子博弈解的形式是非安全子博弈，即划分好子博弈后，假设子博弈之前的博弈过程是固定的。但其缺点是非安全子博弈解缺乏理论支持，在很多情况下效果不佳，因为对历史信息的假设过于绝对，导致其实用性较差。尽管如此，在一些简单的博弈环境下，还是可以用来求解简单的博弈问题。

（2）子博弈重新求解

子博弈重新求解需要明确对手可选的动作范围，以及在上一轮条件下，对手选择各个动作能产生的收益值。子博弈重新求解可以重建一个策略，且只用于博弈的剩余部分。在子博弈重建求解过程中，每个对手会生成上一局态势下选择各动作的得分向量，向量中的每一个元素对应假如采取某一动作的收益值。该策略最大的好处在于增加了博弈主干的边界和子博弈可用的资源。然而，如果主博弈的策略是固定的，选择子博弈的最优解不一定是全局最优的，因为对手选择的动作永远是固定的，计算其他动作的收益值没有意义。另外，当多个动作的收益值相同时，会使策略效果不佳。

（3）最大边际求解

基于子博弈重新求解的最大边际求解[56]技术能够优化子博弈策略，该技术定义了每个信息集的子博弈边际，进入子博弈树将得到一个惩罚值。最大边际能为强化子博弈找到一个纳什均衡策略。强化子博弈能够通过最大化最小边际求解，使用的迭代算法包括EGT[57]和CFR等。最大边际求解是比较保险的，但该策略所求出的解往往会过拟合于假设的模型，所以其效果与子博弈重新求解的效果类似。

4.2.3 面向均衡的博弈策略求解

不完全信息博弈模拟了只包含部分信息的情况下多智能体之间的策略交互，其中最成功的算法簇是CFR算法及其变种。CFR是目前最先进的能够在大型不完全信息博弈中生成高效策略的技术之一，是一种在两人零和博弈中收敛到纳什均衡的迭代算法，并且在两人零和博弈中计算出近似纳什均衡策略的存在性和收敛性都具有理论保障。

遗憾最小化（regret minimization）算法是CFR的前身，由Hart和Greenwald[58-59]将其应用到计算机博弈领域，并在正则博弈游戏中取得了不错的效果。遗憾是一个在线学习概念，引发了一系列强大的学习算法。博弈中遗憾值的作用是根据对过去博弈中行为动作的遗憾程度来调整将来的动作选择策略。

传统上，遗憾最小化方法主要解决的是正则博弈问题。尽管在概念上可以将任何有限的扩展式博弈转换为等价的正则博弈，但表示大小的指数增长使对转换后的博弈使用遗憾算法不切实际，如HUL有多达1017的博弈状态。在如此大规模的博弈树中计算整体最小遗憾是不切实际的。

（1）表格式CFR

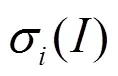
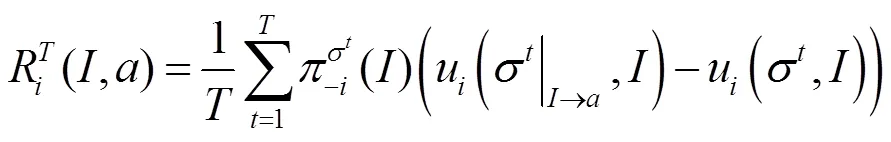
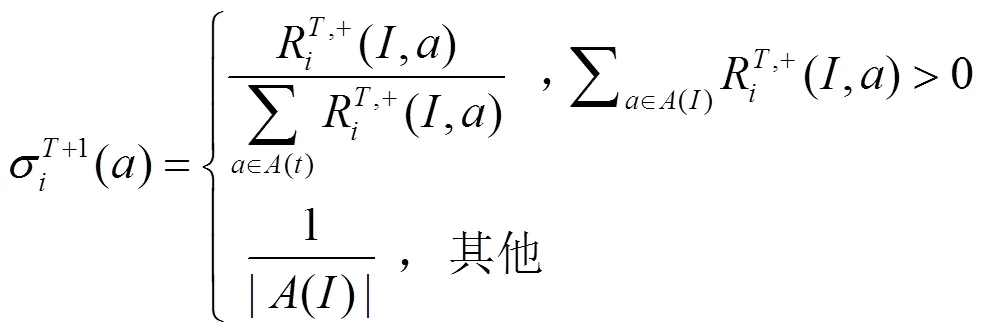
式(7)给出了虚拟遗憾值与更新下一轮策略中的动作概率分布之间的关系，即每种动作被选择的概率与其在已经进行的轮博弈中没被选择而产生的累加的正遗憾值成正比。若遗憾值非正值，则给每个动作按均匀分布并依概率选取。

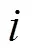
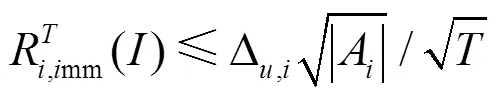
从而有

这一结果表明：平均整体遗憾的上界与信息集的数量呈线性关系，算法需要的迭代次数最多是博弈状态规模的二次方，这成为原始CFR算法的瓶颈之处。随后，各种CFR变体不断出现，突破了原始CFR算法的瓶颈。

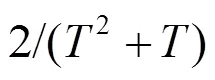
（2）采样类CFR

对于德州扑克这样的大规模博弈而言，使用CFR算法对整个博弈树进行遍历搜索是不可能的，并且CFR算法需要知道对手的策略，这使CFR只能用于训练离线策略而无法进行在线遗憾最小化。2009年，Lanctot等提出基于蒙特卡洛抽样的CFR（MCCFR）算法[66]，每次对抽样到的块（block）进行更新，从而避免了对整棵博弈树搜索，减少收敛所需时间。MCCFR算法衍生出许多鲁棒采样类变体，其中两个具有代表性的是基于结果抽样的蒙特卡洛虚拟遗憾值最小化（OSMCCFR，outcome-sampling Monte Carlo counterfactual regret minimization）算法和基于外部抽样的蒙特卡洛虚拟遗憾值最小化（ESMCCFR，external-sampling Monte Carlo counterfactual regret minimization）算法，前者在每次迭代中只抽样一次博弈，后者抽样机会节点和对手的行为。在合理的抽样策略下，MCCFR算法能使总体遗憾值最小化，因此可以用于计算纳什均衡策略。此外，由于结果抽样不需要对手策略的知识，可以将其用于在线遗憾最小化。

（3）神经网络类CFR

为了处理大规模的不完全信息博弈，通常用抽象方法将相似的状态组合在一起并对它们进行相同的处理来简化博弈。抽象过的简化博弈可以通过表格CFR近似求解。然而，构造一个有效的抽象依赖于广泛的领域知识，抽象解可能只是原博弈问题的一个均衡解的近似。

2018年，Li等提出了一种不完全信息博弈的双神经网络表示方法，称为Double Neural CFR算法[67]。其中一个神经网络表示累积遗憾值，另一个表示平均策略，并采用虚拟遗憾最小化算法来优化这种双神经网络。然而这种方法只考虑了小型博弈。2018年，Noam等在将CFR与深度强化学习相结合提出了Deep CFR算法[68]，它使用深度神经网络来近似CFR在整个博弈中的行为，从而避免了对抽象的需要，相对于领域特定的抽象技术，在不依赖高级领域知识的情况下从样本的状态空间上进行抽象和概括，并取得了很强的性能。这是第一个在大型游戏中取得成功的非表格式的CFR变体。

Deep CFR是基于样本的，不需要计算和存储每个信息集上的遗憾值，而是通过深度神经网络的函数逼近在相似的信息集中进行泛化来近似CFR在整个博弈中的行为，从而避免了对抽象的需要。这也是第一个在大型游戏中取得成功的非表格式CFR变体。Deep CFR中存在两个神经网络分别是值网络和策略网络。值网络的参数为：输入是信息集，输出是累计后悔值。训练的目标是使网络的输出与表格CFR产生的遗憾值近似成比例。在每次迭代中，Deep CFR对博弈树进行一个常数K的部分遍历，遍历路径由外部抽样MCCFR确定。在它遇到的每个信息集上，都会采用由值网络的输出进行遗憾匹配后所得到的策略。一旦玩家的K次遍历完成，一个新的网络被从头开始训练，通过最小化网络的输出值与第次迭代瞬时遗憾值样本之间的均方误差来确定网络参数。除了值网络之外，一个独立的策略网络用于近似CFR算法运行结束时的平均策略。为此，Deep CFR为两个玩家分别保留一个采样信息集概率向量的内存。当一个属于玩家的信息集在对方玩家通过外部抽样遍历博弈树的过程中被遍历时，信息集概率向量被添加到其中并被赋予权重。如果Deep CFR的迭代次数和每个值网络模型的规模很小，那么可以通过存储每次迭代的值网络来避免训练最终的策略网络。在实际游戏过程中，随机抽样一个值网络，玩家对该网络产生的预测值采用遗憾匹配算法得到CFR策略。这消除了平均策略网络的函数逼近所产生的误差，但需要存储所有的值网络。尽管如此，通过仅存储值网络的一部分子集，仍然可以实现强大的性能和低的可利用性。

2018年，Eric提出Deep CFR 的一个新变体（SDCFR，single deep CFR）算法[69]，通过直接使用DeepCFR中的值网络所产生的策略避免了额外训练平均策略网络，减少了总体抽样和平均策略网络所产生的近似误差，但需要存储所有的值网络。从理论上看，SDCFR更具吸引力，它不仅在扑克游戏中提高了Deep CFR的收敛性，并在一对一的比赛中优于Deep CFR。尽管CFR变体在扑克领域取得了许多成就，但是所有已知的CFR变体在理论上都存在一个显著的缺陷——它们在最坏情况下的收敛速度是(−1/2)。针对该问题，Farina等通过将矩阵博弈中乐观遗憾最小化的可预测性和稳定性思想推广到扩展式博弈上，并提出了一个CFR变体[70]，实验表明，该算法在两人零和扩展式博弈中收敛速度达到(−3/4)，这是首个收敛速度优于(−1/2)的CFR变体。

4.2.4 面向非均衡的近似策略求解

目前，在实验结果上表现最佳方法博弈理论框架中，以CFR为核心的算法簇，结合抽象、采样、剪枝、热启动等技术，快速收敛，但CFR具有消耗计算资源大这个明显缺点。并且，基于博弈均衡解近似的方法，由于多人博弈纳什均衡解不满足可交换性，无法从理论上求解不完全信息动态博弈中的多人博弈问题。均衡的搜寻依赖于领域知识和抽象压缩技术，算法很难拓展到其他场景中。本节针对强化学习算法，深度学习和贝叶斯网络等非均衡近似策略方法简要介绍，为解决计算机扑克智能博弈问题提供新思路。

（1）强化学习

强化学习模拟人类在与环境交互中不断学习的过程，是一种自学习算法[71]，也是解决计算机博弈问题常用的算法之一。在具有完美信息的棋牌回合制对抗博弈中，从状态评估器得到策略的方法可以推广到具有完全信息的二人零和博弈。然而，强化学习算法在不完美信息游戏中的应用具有挑战性：①玩家不知道自己在博弈中所处的状态，不能建模成马尔可夫决策过程。基于价值（value-based）的方法，如TD学习、Q学习，不再适用于不完全信息的游戏；②在多智能体共同学习、对手策略未知的情况下环境具有非平稳动态性。Heinrich和Silver提出了一种在不完美博弈中不需要任何先验知识就能学习近似纳什均衡的端到端强化学习方法——神经虚拟自我对弈（NFSP，neural fictitious self play）[72]，将虚拟自我对弈与神经网络函数近似结合起来。一个玩家的网络模型由Q学习网络和监督式学习网络组成，Q学习网络通过贪婪深度Q学习计算最佳响应，监督式学习网通过对智能体历史行为的监督学习计算平均策略。NFSP通过引入预期动态来解决协调问题——玩家根据平均策略和最佳反应展开行动。然而，由于对手策略的复杂性和DQN在离线模式下学习的特点，NFSP在搜索空间和搜索深度规模较大的博弈中表现较差。浙江大学研究人员提出了蒙特卡洛神经虚拟自我对弈（MCNFSP，Monte Carlo neural fictitious self play）算法，该算法结合了NFSP与蒙特卡洛树搜索（模型结构如图4所示）。研究人员在二人零和Leduc扑克中评估了该方法。实验表明，MCNFSP将收敛到近似纳什均衡，但NFSP无法做到。NFSP的另一个缺点是最佳反应依赖于深度Q学习的计算，需要很长时间网络才能收敛。Zhang等针对该缺点进一步改进算法，提出了异步神经虚拟自我对弈[35]（ANFSP，asynchronous neural fictitious self play）方法，使用并行的动作学习来稳定和加速训练，多个玩家并行进行决策。玩家分享Q学习网络和监督学习网络，在Q学习中累积多个步骤的梯度，并在监督学习中计算小批量的梯度。与NFSP相比，这减少了数据存储所需的内存。研究人员在二人零和扑克游戏中评估了该方法。实验表明，与NFSP相比，ANFSP可以更加稳定和快速地接近近似纳什均衡。

图4 MCNFSP中的DQN模型结构

Figure 4 DQN architecture in MCNFSP

强化学习算法的创新、改进和验证依赖于商业巨头开发的测试平台和算法框架。现有的强化学习库多数是单智能体环境的（如OpenAI Gym），支持多智能体的环境多数是即时策略游戏，支持牌类游戏的环境较少。文献[73]的OpenHoldem平台虽然提供了较强的测试基准AI，但目前还缺少强化学习框架以及相关接口。文献[74]提供了专为牌类游戏设计的测试平台RLCard，不仅是一些棋牌类游戏在强化学习库中的首次实现，也提供了简单直观的接口，便于强化学习研究。

（2）深度学习

深度学习是一种数据驱动的方法，在算法的扩展性上具有很大的优势。深度学习应用在多人在线战略游戏（MOBA，multi-player online battle arena）上取得了巨大的成功，但在扑克等棋牌游戏上研究进展缓慢。Nikolai[75]等针对HULTH的特点，将私有牌、公共牌、奖金池、玩家位置等游戏信息表示成31×17×17的张量，使用两个启发式的玩家进行10万手（通常称扑克中的一局完整游戏为一手）的对弈生成50万个样本，使用CNN模型（如图5所示）进行训练，学习下注动作，并多次重复这个自我对弈的循环。每一轮的自我对弈都是由最新的CNN模型与前三个模型进行博弈，以避免过度优化当前最优模型的弱点。但通过数据驱动的方法构建扑克游戏系统同样面临挑战。①博弈信息的表示。学习模型需要能够在不同扑克游戏中具有丰富信息量的表示。②复杂性。从简单启发式对手获得的数据不足以用来训练一个有竞争性且高水平的扑克AI。

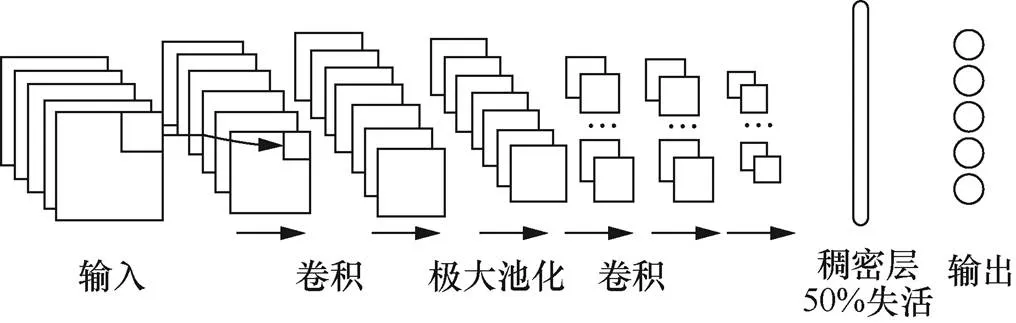
图5 扑克CNN结构

Figure 5 CNN architecture for poker

（3）贝叶斯网络

贝叶斯网络（BN，Bayesian networks）是人工智能领域中一个非常成熟的不确定性推理工具。每个贝叶斯网络都是一个有向无环图（如图6所示），图中的每个节点代表一个随机变量，图中节点之间的边表示依赖关系。网络中的每个节点都有一个相关的条件概率表（CPT），它允许根据父节点的值计算条件概率值。通过给网络中的节点分配不同的值，概率可以在整个网络中传播，从而形成随机变量上的概率分布。

图6 贝叶斯网络

Figure 6 Bayesian network

决策网络也称为影响图，是支持决策制定的BN的扩展，显式地表示决策和成本/收益，或更一般地表示结果的效用。通过将概率推理与效用相结合，决策网络有助于做出最大化预期效用的决策。Korb将贝叶斯网络从5张牌的加勒比扑克（5-card Stud Poker）迁移应用到德州扑克[76]，设计了用于顺子和同花顺预测的贝叶斯决策网络，产生了BPP（Bayesian poker program）的扑克AI。BPP所使用的网络（如图7所示）由变量组成，如桌上的筹码数量、对手的动作、BPP的当前手型和最终手型、对手的当前手型和最终手型。

BPP在2006年的ACPC比赛资金竞争赛中获得第三名，在即时决胜竞争赛中获得第四名，但在2007年的ACPC比赛中，BPP输给了所有参赛AI。

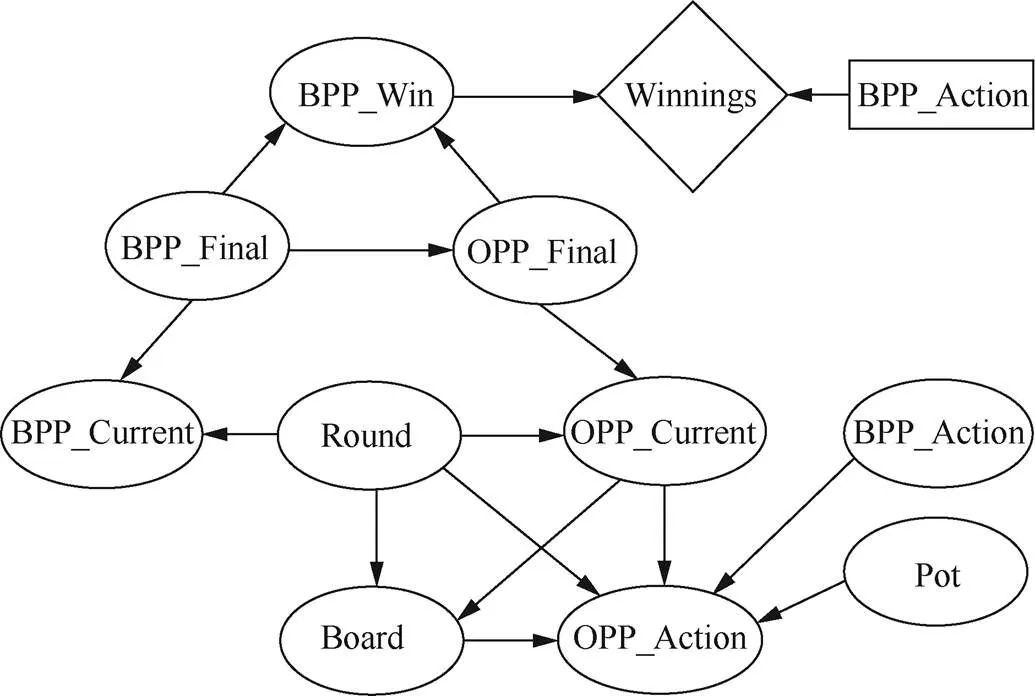
图7 德州扑克决策网络

Figure 7 Decision network of Texas Hold'em poker

5 计算机扑克智能博弈的研究展望

随着不完全信息动态博弈理论的不断发展，越来越多的实际问题得到了解决。多人德州扑克博弈的突破对不完全信息动态博弈理论的发展起到了巨大的推动作用。然而，当前的不完全信息动态博弈在理论与应用方面依然存在一些不足，如何解决这些问题并将不完全信息动态博弈推向更广阔的应用场景将是未来的研究主题。

5.1 多人纳什均衡

Pluribus虽然在多人德州扑克中通过精心设计的机器学习算法战胜人类职业选手，但仍缺乏理论上证明最优策略是如何获取的。即使可以在多人博弈中有效地计算纳什均衡，但采取这样的纳什均衡策略并不一定是“明智”的。如果博弈中的每个玩家都独立地计算和采取纳什均衡策略，那么他们的策略组合可能并不是纳什均衡，并且玩家可能具有偏离到不同策略的动机。以柠檬水看台游戏为例[4]，如图8所示，每个玩家需要在圆环中找到一个位置，使自己与其他所有玩家的距离总和最远（左图），则纳什均衡就是所有玩家沿环均匀分布，并有无限多的方法可以实现这一点，因此有无限多的纳什均衡。但如果每个人都独立计算自己的纳什均衡策略，那么最终可能不会有纳什均衡出现（右图）。而两人零和博弈就不会存在这样的问题，即使两人独立计算和选择纳什均衡，其策略剖面仍然是纳什均衡。在三人及以上玩家的游戏中不能简单地计算出一个纳什均衡并且按照其给出的策略行动，因为难于保证其他玩家是否会选择同一个均衡的策略，所以需要新的技术来处理，并且需要决定如何评估模型在这些游戏中的性能。如何在理论上证明多人无限注德州扑克的最优策略是否存在、如果存在怎样计算、与博弈的均衡策略之间的关系等问题，还需要研究者进行不断的探索。

5.2 有限理性对手与欺骗

对手模型的内容可以是博弈过程中玩家表现出的选择偏向、玩家采用的策略、玩家暴露出的弱点或关于玩家博弈能力的评估等，只要是博弈过程中对手可被利用的信息都可以出现在对手模型中。在线对手建模过程中，通常假设对手是完全理性的，但由于人类存在的感性因素或者情绪影响，实际扑克游戏过程中的人类对手是理性受限的。随着游戏的不断重复，高水平的人类玩家能够逐渐适应对手的打法，动态调整自己的策略，甚至故意采用“慢打”（slow-playing）[13]“诈唬”（bluff）[78]“半诈唬”（semi-bluff）等手段混淆欺骗，扰乱对手对自身的认知。慢打和诈唬等欺骗方法是认知博弈对抗中的难点。现存研究缺少对欺骗的定量描述以及对欺骗的识别与反制。Teppo Salonen设计的采用诈唬策略的德州扑克智能体BluffBot在2006年ACPC比赛取得第二名的成绩。未来研究中，如何有效利用欺骗手段开发高水平的AI，如何在线建模人类对手的过程中识别对手的欺骗，或者如何权衡长期收益与当前收益之间的关系有待继续深入研究。

5.3 通用对抗博弈AI

大部分智能算法在几个特定的场景中能表现出优越的性能，一旦脱离固定的场景，则迁移到相似的一类场景中，但未必能保持各项指标的优越。例如，LCFR在Kuhn扑克中能够快速收敛，性能优于ECFR。但在Leduc扑克中，表现稍逊色，不仅收敛性变慢，可利用性也变大[79]。通用对抗博弈AI的研究目标是拓宽AI算法的通用性和可行性，是AI研究的先进前沿方向之一，旨在寻求一个与领域无关的解决方案。目前，通用对抗博弈AI的研究不仅需要算法层面的突破，更需要通用博弈对抗设计上的突破。目前成熟的通用对抗博弈环境，包括通用对弈竞赛、街机学习环境以及通用视屏游戏，为通用博弈对抗AI提供了测试基准。虽然通用性是长期的研究目标，但并不代表单个任务单个游戏中的算法研究是无用的，因为通用系统存在内在风险——模型算法过于通用以至于在现实问题中无法找到特定的应用[80]。

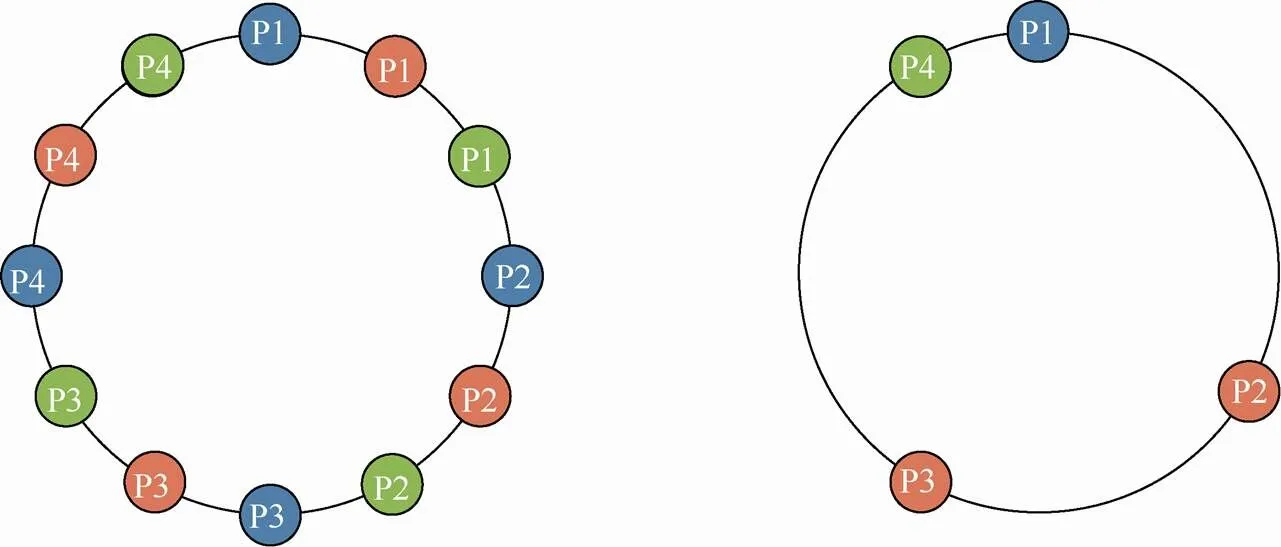
图8 柠檬水看台游戏

Figure 8 Lemonade stand game

6 结束语

认知智能主要研究如何提高智能体理解、推理、思考和决策等能力。在“巨复杂、高动态、强对抗”环境中，人类的感知和决策能力受限人类个体的物理限制，迫切需要以机器为载体的认知智能辅助决策。计算机智能博弈是人工智能认知决策领域的“果蝇”，因边界确定、规则固定，备受人工智能领域研究者的关注，已然成为研究认知智能极佳的试验环境和验证途径。计算机在认知智能方面才刚刚起步，还未达到人类水平，尤其在不完美信息博弈中，面对“状态信息大规模、私有信息隐藏、对手行为高度欺骗”等问题特性，模型建立复杂，求解困难。本文着眼于智能化时代智能需求，以计算机扑克为切入点，分析计算机扑克复杂度，探索智能博弈中不完全信息博弈的关键技术，阐述了以德州扑克为代表的计算机扑克智能博弈的发展历程、问题表示与建模、关键技术以及存在的主要问题。计算机扑克智能博弈的研究虽然已经有丰硕的成果，但如何在博弈论的框架内从理论上攻克多人难题，以及如何迁移应用到现实世界中，仍然是值得研究的问题。

[1] 兴军亮.人工智能新突破：AI程序攻克多人无限注德州扑克[EB]. XING J L. The new breakthrough of artificial intelligence:AI program conquered multiplayer unlimited Texas Hold 'em[EB].

[2] SILVER D, HUANG AJA, MADDISON C J, et al. Mastering the game of Go with deep neural networks and tree search[J]. Nature, 2016, 529(7587):484489.

[3] SILVER D, SCHRITTWIESER J, SIMONYAN K, et al. Mastering the game of Go without human knowledge[J]. Nature,2017, 550(7676):354359.

[4] BLAIR A, SAFFIDINE A. AI surpasses humans at six-player poker[J]. Science, 2019, 365(6456): 864865.

[5] MORAVCIK, MATEJ, SCHMID M , et al. DeepStack: expert-level artificial intelligence in heads-up no-limit poker[J]. Science, 2017: 6960.

[6] NOAM B, TUOMASS. Superhuman AI for heads-up no-limit poker: Libratus beats top professionals[J]. Science:eaao1733.

[7] JIANG Q, LI K, DU B, et al. DeltaDou: expert/level doudizhu AI through self-play[C]//Proceedings of the 28th International Joint Conference on Artificial Intelligence. 2019: 12651271.

[8] LI J, KOYAMADA S, YE Q, et al. Suphx: mastering mahjong with deep reinforcement learning[J]. arXiv preprint arXiv:2003.13590, 2020.

[9] BERNER C, BROCKMAN G, CHAN B, et al. Dota 2 with large scale deep reinforcement learning[J]. arXiv preprint arXiv:1912.06680, 2019.

[10] YE D, LIU Z, SUN M, et al. Mastering complex control in MOBA games with deep reinforcement learning[J]. arXiv preprint arXiv:1912.09729, 2019.

[11] 朱建明,高博. 社交金融的信息安全风险分析与防范[J]. 网络与信息安全学报, 2016, 2(3): 46-51.

ZHU J M, GAO B. Social financial information security risk analysis and prevention[J]. Chinese Journal of Network and Information Security, 2016, 2(3): 46-51.

[12] 杨峻楠,张红旗,张传富. 基于不完全信息随机博弈的防御决策方法[J]. 网络与信息安全学报, 2018, 4(8): 12-20.

YANG J N, ZHANG, H Q ZHANG C F, Defense decision-making method based on incomplete information stochastic game[J]. Chinese Journal of Network and Information Security, 2018, 4(8): 12-20.

[13] PAPP D R. Dealing with imperfect information in poker[R]. 1998.

[14] BILLINGS D, DAVIDSON A, SCHAEFFER J, et al. The challenge of poker[J]. Artificial Intelligence, 2002, 134(12): 201-240.

[15] BILLINGS D, BURCH N, DAVIDSON A, et al. Approximating game­theoretic optimal strategies for full­scale poker[C]//IJCAI. 2003: 661.

[16] SCHAUENBERG T C. Opponent modelling and search in poker[D]. Edmonton: University of Alberta, 2009.

[17] ZINKEVICH M, JOHANSON M, BOWLING M, et al. Regret minimization in games with incomplete information[C]//Advances in Neural Information Processing Systems. 2008: 1729­1736.

[18] JOHANSON M B. Robust strategies and counter­strategies: from superhuman to optimal play[D]. Edmonton: University of Alberta, 2009.

[19] SCHNIZLEIN D. State translation in no­limit poker[D]. Edmonton: University of Alberta, 2009.

[20] ABOU R N, SZAFRON D. Using counterfactual regret minimization to create competitive multiplayer poker agents[C]//Proceedings of the 9th International Conference on Autonomous Agents and Multiagent Systems. 2010: 159­166.

[21] GILPIN A, SANDHOLM T, SORENSEN T B. A heads­up no­limit Texas Hold’em poker player: discretized betting models and automatically generated equilibrium­finding programs[C]//Proceedings of the 7th International Joint Conference on Autonomous Agents and Multiagent Systems, 2008: 911­918.

[22] BROWN N, GANZFRIED S, SANDHOLM T. Tartanian7:a champion two­player no­limit texas hold’em poker­playing program[C]//Twenty­9 AAAI Conference on Artificial Intelligence. 2015.

[23] GANZFRIED S. Reflections on the first man vs. machine no­limit Texas Hold'em competition[J]. ACM SIGecom Exchanges, 2016, 14(2): 2­15.

[24] BROWN N, SANDHOLM T. Baby Tartanian8: winning agent from the 2016 annual computer poker competition[C]//IJCAI. 2016: 4238­4239.

[25] BILLINGS D, BURCH N, DAVIDSON A, et al. Approximating game-theoretic optimal strategies for full-scale poker[C]//Proceedings of the Eighteenth International Joint Conference on Artificial Intelligence. 2003: 661-668.

[26] STURTEVANT N, BOWLING M. Robust game play against unknown opponents[C]//Proceedings of the fifth International Joint Conference on Autonomous Agents and Multiagent Systems. 2006: 713-719.

[27] JOHANSON M B. Robust strategies and counter­ strategies: building a champion level computer poker player[D]. Edmonton: University of Alberta, 2007.

[28] ZINKEVICH M , JOHANSON M , BOWLING M H, et al. Regret minimization in games with incomplete information[C]//International Conference on Neural Information Processing Systems. 2007.

[29] ABOU RISK N, SZAFRON D. Using counterfactual regret minimization to create competitive multiplayer poker agents[C]//Proceedings of the 9th International Conference on Autonomous Agents and Multiagent Systems. 2010 1: 159­166.

[30] BOWLING M, BURCH N, JOHANSON M, et al. Heads­up limit hold’em poker is solved[J]. Science, 2015, 347(6218): 145­149.

[31] LOCKHART E, LANCTOT M, PEROLAT J, et al. Computing approximate equilibria in sequential adversarial games by exploitability descent[J]. arXiv preprint arXiv:1903.05614, 2019.

[32] BROWN N, SANDHOLM T, AMOS B. Depth-limited solving for imperfect-information games[C]//Advances in Neural Information Processing Systems. 2018: 7663-7674.

[33] BROWN N, LERER A, GROSS S, et al. Deep counterfactual regret minimization[C]//International Conference on machine learning. PMLR. 2019: 793-802.

[34] PASSOS N M S. Poker learner: reinforcement learning applied to Texas Hold’em poker[D]. Porto: The University of Porto, 2011.

[35] ZHANG L, WANG W, LI S, et al. Monte Carlo neural fictitious self-play: achieve approximate nash equilibrium of imperfect-information games[J]. arXiv preprint arXiv: 1903.09569v2, 2019.

[36] ZHANG J, WANG X, YAO L, et al. Using risk dominance strategy in poker[J]. Journal of Information Hiding and Multimedia Signal Processing, 2014, 5(3): 546-554.

[37] 滕雯娟. 基于虚拟遗憾最小化算法的德州扑克机器博弈研究[D]. 哈尔滨: 哈尔滨工业大学, 2015.

TENG W J. Research on texas poker game based on counterfactual regret minimization algorithm[D]. Harbin: Harbin Institute of Technology, 2015.

[38] 代佳宁. 基于虚拟遗憾最小化算法的非完备信息机器博弈研究[D].哈尔滨: 哈尔滨工业大学, 2017.

DAI S N. Research on imperfect information game based on counterfactual regret minimization algorithm[D]. Harbin : Harbin Institute of Technology, 2017.

[39] SKLANSKY D. The theory of poker[M]. Two plus two publishing LLC, 1999.

[40] SKLANSKY D, MALMUTH M. Hold'em poker for advanced players[M]. Two Plus Two Publishing LLC, 1999.

[41] JOHANSON M. Measuring the size of large no-limit poker games[J]. arXiv preprint arXiv:1302.7008, 2013.

[42] BORGHETTI B J . Opponent modeling in interesting adversarial environments[M]. Minnesota: University of Minnesota, 2008.

[43] WRIGHT J R. Modeling human behavior in strategic settings[D]. COLUMBIA: University of British Columbia, 2016.

[44] PLONSKY O, APEL R, ERT E, et al. Predicting human decisions with behavioral theories and machine learning[J]. arXiv preprint arXiv:1904.06866, 2019.

[45] 高巍, 罗俊仁, 袁唯淋, 等. 面向对手建模的意图识别方法综述[J].网络与信息安全学报, 2021, 7(4): 86-100.

GAO W, LUO J R, YUAN W L, et al. A survey of intention recognition for opponent modeling[J]. Chinese Journal of Network and Information Security, 2021, 7(4): 86-100.

[46] HOEHN B, SOUTHEY F, HOLTE R C, et al. Effective short-term opponent exploitation in simplified poker[C]//AAAI. 2005: 783-788.

[47] GANZFRIED S, SANDHOLM T. Game theory-based opponent modeling in large imperfect-information games[C]//The 10th International Conference on Autonomous Agents and Multiagent Systems-Volume 2. 2011: 533-540.

[48] NORRIS K, WATSON I. A statistical exploitation module for Texas Hold'em: and it's benefits when used with an approximate Nash equilibrium strategy[C]//2013 IEEE Conference on Computational Inteligence in Games (CIG). 2013: 1-8.

[49] GANZFRIED S, SANDHOLM T. Safe opponent exploitation[J]. ACM Transactions on Economics and Computation (TEAC), 2015, 3(2): 1-28.

[50] SANDHOLM T. The state of solving large incomplete­information games, and application to poker[J]. AI Magazine, 2010, 31(4): 13­32.

[51] SANDHOLM T. Solving imperfect­information games[J].Science, 2015, 347(6218): 122­123.

[52] SANDHOLM T. Abstraction for solving large incomplete­information games[C]//29 AAAI Conference on Artificial Intelligence. 2015.

[53] GILPIN A, SANDHOLM T. Lossless abstraction of imperfect information games[J]. Journal of the ACM (JACM), 2007, 54(5).

[54] GILPIN A, SANDHOLM T. Better automated abstraction techniques for imperfect information games, with application to Texas Hold’em poker[C]//Proceedings of the 6th International Joint Conference on Autonomous Agents and Multiagent Systems. 2007: 1­8.

[55] NOAM B, GANZFRIED S, SANDHOLM T. Hierarchical abstraction, distributed equilibrium computation,and post­processing, with application to a champion no­limit Texas Hold'em agent[C]// Workshops at the 29 AAAI Conference on Artificial Intelligence. 2015.

[56] BROWN N, SANDHOLM T. Safe and nested subgame solving for imperfect­information games[C]//Advances in Neural Information Processing Systems. 2017: 689­699.

[57] NESTEROV. Excessive gap technique in nonsmooth convex minimization[J]. SIAM Journal of Optimization, 2005, 16(1): 235-249.

[58] HART S A, MAS D, COLELL A. A simple adaptive procedure leading to correlated equilibrium[J]. Econometrica, 2000, 68(5): 1127-1150.

[59] GREENWALD A, LI Z, MARKS C. Bounds for regret-matching algorithms[C]//Proceedings of the 9 International Symposium on Artificial Intelligence and Mathematics. 2005.

[60] GIBSON R G, LANCTOT M, BURCH N, et al. Generalized sampling and variance in counterfactual regret minimization[C]//Proceedings of the Twenty­Sixth Conference on Artificial Intelligence. 2012: 3690­3706.

[61] LISY V, LANCTOT M, BOWLING M. Online monte carlo counterfactual regret minimization for search in imperfect information games[C]//Proceedings of the 2015 International Conference on Autonomous Agents and Multiagent Systems. 2015:27­36.

[62] GANZFRIED S, SANDHOLM T. Endgame solving large imperfect-information games[C]//Workshops at the Twenty-Ninth AAAAI Conference on Artificial Intelligence. 2015.

[63] BROWN N, SANDHOLM T. Solving imperfect­information games via discounted regret minimization[C]//AAAI Conference on Artificial Intelligence (AAAI). 2019.

[64] BROWN N, SANDHOLM T. Regret­based pruning in extensive form games[C]//Advances in Neural Information Processing Systems. 2015: 1972­1980.

[65] BROWN N, SANDHOLM T. Strategy­based warm starting for regret minimization in games[C]//Proceedings of 30 Conference on Artificial Intelligence. 2015:432­438.

[66] LANCTOT M, WAUGH K, ZINKEVICH M, et al. Monte Carlo sampling for regret minimization in extensive games[C]//Advances in Neural Information Processing Systems. 2009: 1078-1086.

[67] LI H, HU K, GE Z, et al. Double neural counterfactual regret minimization[J]. 2018.

[68] NOAM B, LERER A, GROSS S, et al. Deep counterfactual regret minimization[J]. axXiv Preprint arXiv: 1812.10607, 2018.

[69] ERIC S. Single deep counterfactual regret minimization[J]. arXiv Preprint arXiv: 1901.07621, 2018.

[70] FARINA G, KROER C, BROWN N, et al. Stable­predictive optimistic counterfactual regret minimization[C]//International Conference on Machine Learning. 2019: 1853-1862.

[71] 陈学松, 杨宜民. 强化学习研究综述[J]. 计算机应用研究, 2010(8): 40­44, 50.

YANG X S, CHEN Y M. Reinforcement learning：survey of recent work[J]. Application Research of Computers, 2010(8): 40-44, 50.

[72] HEINRICH J, SILVER D. Deep reinforcement learning from self-play in imperfect-information games[J]. arXiv preprint arXiv:1603.01121, 2016.

[73] LI K, XU H, ZHANG M, et al. OpenHoldem: an open toolkit for large-scale imperfect-information game research[J]. arXiv preprint arXiv:2012.06168, 2020.

[74] ZHA D, LAI K H, CAO Y, et al. RLCard: a toolkit for reinforcement learning in card games[J]. arXiv preprint arXiv:1910.04376, 2019.

[75] NIKOLAI Y, CAO L, RAFFEL C, et al. Poker-CNN: a pattern learning strategy for making draws and bets in poker games using convolutional networks[C]//30 AAAI Conference on Artificial Intelligence. 2016.

[76] KORB K B, NICHOLSON A, JITNAH N. Bayesian poker[J]. arXiv preprint arXiv:1301.6711, 2013.

[77] GANZFRIED S, SANDHOLM T. Endgame solving in large imperfect information games[C]//Proceedings of the 2015 International Conference on Autonomous Agents and Multiagent Systems. 2015: 37-45.

[78] SOUTHEY F, BOWLING M P, LARSON B, et al. Bayes' bluff: opponent modelling in poker[J]. arXiv preprint arXiv:1207.1411, 2012.

[79] LI H, WANG X, JIA F, et al. RLCFR: minimize counterfactual regret by deep reinforcement learning[J]. arXiv preprint arXiv:2009.06373, 2020.

[80] YANNAKAKIS G N, TOGELIUS J. Artificial intelligence and games[M]. New York: Springer, 2018.

Survey on intelligent game of computer poker

YUAN Weilin, LIAO Zhiyong, GAO Wei, WEI Tingting, LUO Junren, ZAHNG Wanpeng, CHEN Jing

College of Intelligence Science and Technology, National University of Defense and Technology, Changsha 410073, China

Computer game is the drosophila in the field of artificial intelligence, which has attracted the attention of researchers in artificial intelligence, and has become an advantageous testbed for the research of cognitive intelligence. Poker game can be modeled as dynamic games with imperfect information, definite boundaries and fixed rules. Computer poker AI needs such abilities as dynamic decision-making with incomplete information, identification of misleading and fraudulent behaviors by opponents, and multi-round chips and risk management. Firstly , the development of computer poker game was introduced, which represented by Texas Hold’em poker. Then, typical intelligence game model algorithm, key techniques and existing main problems of computer poker were reviewed analysis. Finally, the future development trends and application prospect of computer intelligent poker game were discussed for cognitive intelligence.

computer poker, cognitive intelligence, imperfect information game, Texas Hold'em poker, Counterfactual regret minimization

TP18

A

10.11959/j.issn.2096−109x.2021087

2020−11−19；

2021−03−06

张万鹏，wpzhang@nudt.edu.cn

国家自然科学基金（61702528，61806212）

The National Natural Science Foundation of China (61702528, 61806212）

袁唯淋, 廖志勇, 高巍, 等. 计算机扑克智能博弈研究综述[J]. 网络与信息安全学报, 2021, 7(5): 57-76.

YUAN W L, LIAO Z Y, GAO W, et al. Survey on intelligent game of computer poker[J]. Chinese Journal of Network and Information Security, 2021, 7(5): 57-76.

袁唯淋（1994−），男，云南曲靖人，国防科技大学博士生，主要研究方向为认知决策与智能博弈、对手建模、强化学习、多智能体系统。

廖志勇（1995−），男，湖南永州人，国防科技大学硕士生，主要研究方向为知识图谱、智能决策、网络通信。

高巍（1996−），女，辽宁开原人，国防科技大学硕士生，主要研究方向为对手建模、意图识别、弹道规划。

魏婷婷（1997−），女，内蒙古鄂尔多斯人，国防科技大学硕士生，主要研究方向为智能体建模、智能博弈、多智能体强化学习。

罗俊仁（1989−），男，湖北大冶人，国防科技大学博士生，主要研究方向为智能体建模、对抗团队博弈、多智能体强化学习。

张万鹏（1981−），男，四川邛崃人，国防科技大学副研究员，主要研究方向为智能决策、任务规划、自动化和控制、人机协同。

陈璟（1972−），男，江西南昌人，国防科技大学教授、博士生导师，主要研究方向为人工智能、智能决策、任务规划。