基于CFD的洗扫车水力系统的喷嘴分析与优化
朱玉伦,郝淑英,刘 君,张琪昌
(1.天津理工大学a.天津市先进机电系统设计与控制重点实验室,b.机电工程国家级实验教学示范中心,天津300384;2.郑州宇通重工有限公司,郑州450001;3.天津大学天津市非线性动力学与控制重点实验室机械工程学院,天津300072)
随着城市化进程加快,对高清洗效率洗扫车的需求日益增加[1]。洗扫车结合了扫路车、高压清洗车和洒水车的多重功能,对路面清扫的同时还可实现对路面的高压冲洗,清洁效果好,作业无扬尘,特别适用于城市道路等的深度清扫[2]。扇形喷嘴是洗扫车清洗设备的重要组件,其结构及结构参数直接影响射流性能、清洗质量、功率损耗和清洗成本[3]。
为更有效地提升扇形喷嘴的清洗性能,国内外学者分别采用数值模拟和试验分析两种方法对结构参数影响射流性能进行了研究。梁博键等[4]研究了出口扩张角等结构参数对射流性能的影响,得出了能够使喷嘴获得较好的清洗效果的结构参数。欧阳联格等[5]采用数值模拟的方法研究了射流过程中入口压力等参数对清洗效果的影响规律。王国志等[6]研究了切槽形状和加工方式对清洗效果的影响。于兰英等[7]运用Fluent的流体体积(volume of fluid,VOF)两相流模型对不同出口直径的扇形喷嘴在不同压力下的打击力和动压进行了比较分析,研究发现喷嘴直径和压力的增大都会使打击力增大。李喆等[8]分析了打击距离和打击角度对清洗效果的影响,从而确定了更为合理的射流参数。高传昌等[9]运用正交试验方法对自激吸气脉冲射流喷嘴的吸气性能和冲击性能进行了试验研究,并通过极差和方差分析研究了喷嘴面积比和相对腔内面积等因素及其交互作用对装置的工作性能的影响。SHEN等[10]以锥形收敛喷嘴为研究对象,进行正交试验设计,对喷嘴出口速度的质量特性进行了研究。
目前将试验设计引入到扇形喷嘴研究中的人越来越多,但多数情况下,只是考虑单因素结构参数对于射流性能的影响[11-12],很少有研究全面的考虑多个结构因素及其交互作用对扇形喷嘴的射流性能的影响。
本文采用正交试验的方法对某洗扫车所使用的某型号的喷嘴进行了优化设计,研究了扇形喷嘴的收缩段角度、相贯深度、出口扩张角这3个结构参数及其交互作用对扇形喷嘴的射流性能的影响,确定出扇形喷嘴的结构参数的最优组合;应用有限元分析的方法对优化结果进行了仿真和验证,验证了优化结果的有效性。研究结果为喷嘴结构参数的优化,提升扇形喷嘴的射流性能,从而提升洗扫车的清洗效果提供了理论依据。
1 扇形喷嘴的结构与清洗原理
图1为某洗扫车用扇形喷嘴结构剖面图,该扇形喷嘴安装在作业喷杆上,洗扫车水箱中的水在高压泵的作用下通过作业喷杆流向该扇形喷嘴,该喷嘴的结构参数对水帘形状、打击力以及流量等有着重要的影响。
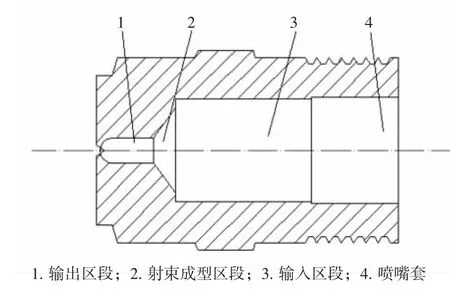
图1 扇形喷嘴结构剖面图Fig.1 Sectional drawing of sector nozzle structure
图2 为喷嘴结构参数示意图。喷嘴出口由V形槽与半球收缩段相贯而成,该出口结构使得水射流形成扁平的扇形流束,其结构参数决定了喷嘴外部射流形状以及性能。选取了收缩段角度α、相贯深度h、出口扩张角θ作为需要优化的结构参数,喷嘴的其他结构尺寸均由所切开的喷嘴实物模型测量得到。

图2 喷嘴结构参数示意图Fig.2 Schematic diagram of nozzle structural parameters
洗扫车的清洗原理是高压水从扇形喷嘴射出,打向地面,通过高压水的打击力来剥离地面上的污垢,再通过车厢底盘中央的吸口将污垢吸走。因此,水射流打击力是衡量喷嘴射流性能的一个很重要的评价指标。另外,由于洗扫车作业时的载水量一定,为了使一次作业的清洗效率尽可能达到最大,喷嘴出口处水流量也是一个需要考虑的重要指标。
2 喷嘴结构参数优化设计
由于洗扫车作业的载水量一定,因此为了使一次作业的清洗效率尽可能达到最大,将打击力和流量作为评价指标,对影响该指标的结构参数进行改进,使用试验优化设计的方法进行寻优,得出提升清洗效率的结构参数,达到既提升清洗效率又节省能源这一目标。
2.1 试验水平的选取
试验因素及水平如表1所示。
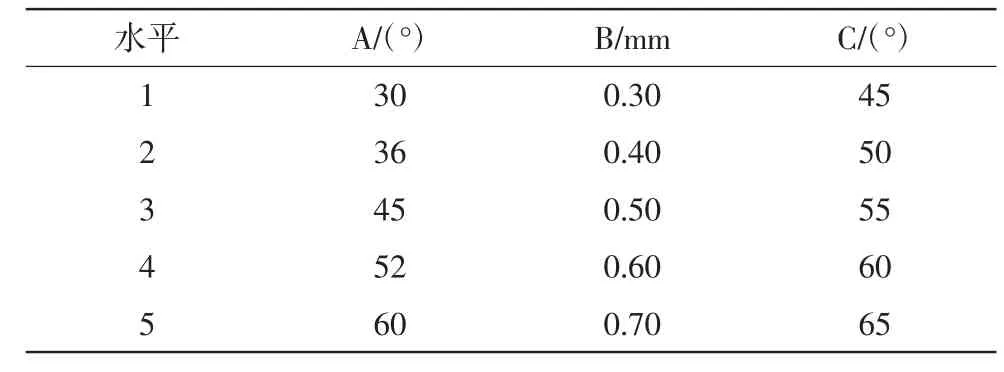
表1 试验因素及水平Tab.1 Test factors and levels
为了反映出各个结构参数对扇形喷嘴的射流性能的影响,采用正交试验设计,用A表示收缩段角度的变化,B表示相贯深度的变化和C表示出口扩张角的变化等3个因素,从实物喷嘴的量级范围内对这3个因素分别选取5个水平。
2.2 试验设计
正交试验是一种研究多因素多水平的设计方法,它根据正交性从全面试验中挑选出部分有代表性的点进行试验,使试验点在试验范围内均匀分散,能反映出全面的情况。文中试验是三因素五水平正交试验,根据正交试验表设计出试验组数,再通过Fluent进行试验仿真获取打击力和流量,得到的部分有代表性的正交试验方案及仿真结果如表2所示。

表2 正交试验方案及仿真结果Tab.2 Orthogonal test scheme and simulation results
2.3 结构参数方差分析
2.3.1 打击力方差分析
方差分析在多因素试验中,可以帮助人们发现起主导作用的因素,从而确定试验中各因素影响作用的主要性及次要性。影响清洗效率的因素有收缩段角度、相贯深度和出口扩张角3种,为了探索各因素对清洗效率的影响作用,使设计工作简单化,因此对打击力和流量进行了方差分析。
根据试验设计的方差,表3为打击力方差分析,p-value<0.05的时候,代表此因子显著,即对结果的影响大;3个结构参数对打击力影响强弱的顺序为:B>C>A,3种结构参数两两之间的交互作用对打击力的影响很小。
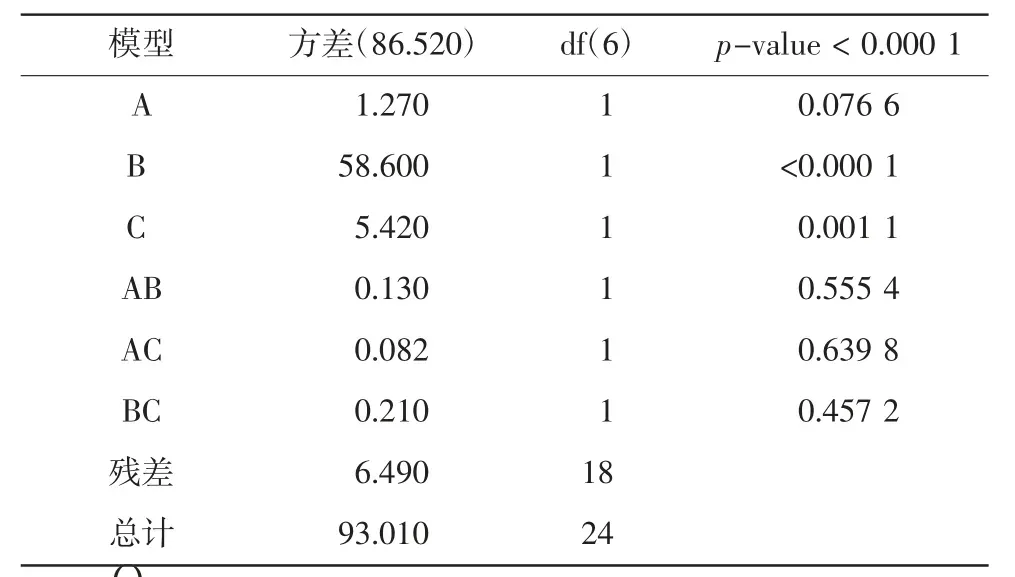
表3 打击力方差分析Tab.3 Variance analyses of strike force
正交试验法可以通过极差反映各因素及其交互作用对评价指标的影响,极差越大说明该因素对指标的影响越大。将各水平所对应的试验结果之和记为ki,i为各水平的代号,各水平从小到大排列,记为1~5,例如A因素所在的第2列中,第1、5和10号实验中因素A的水平是30,记为k1,所以k1为第1、5和10号实验结果之和,即:k1=2.713+1.831+7.863=12.407。
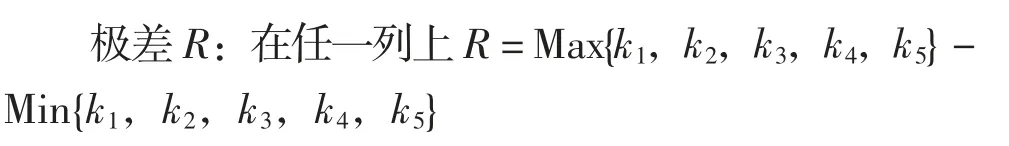
同理可以计算出其他列中的R,打击力试验方差如表4所示。

表4 打击力试验方差Tab.4 Impact test variance
各列的极差是不相等的,说明各因素的水平改变对试验结果影响是不相同的。极差越大,表示该列因素的数值在试验范围内的变化会导致试验指标在数值上有更大的变化,所以极差最大的那一列,就是因素水平对实验结果影响最大的,由3个因素的极差,可以看出RB>RC>RA,因此各因素从主到次的顺序为:B(相贯深度),C(出口扩张角),A(收缩段角度),这也验证了前面依据p-value值所得出的结构参数对打击力影响的分析结果。
在试验中,试验指标是打击力大小,指标越大越好。显然,对于因素A来说,水平1是最好的,即收缩段角度应选取30°;对于因素B来说,水平4是最好的,即相贯深度应选取0.600mm;对于因素C来说,水平5是最好的,即出口扩张角应选取65°。
2.3.2 流量方差分析
根据表5流量方差分析可知,3个结构参数对流量的影响顺序是:B>C>A,比较p-value,3种结构参数两两之间的交互作用对流量虽有影响,但影响较小,考虑到试验及人工的成本,此处忽略交互作用的影响。
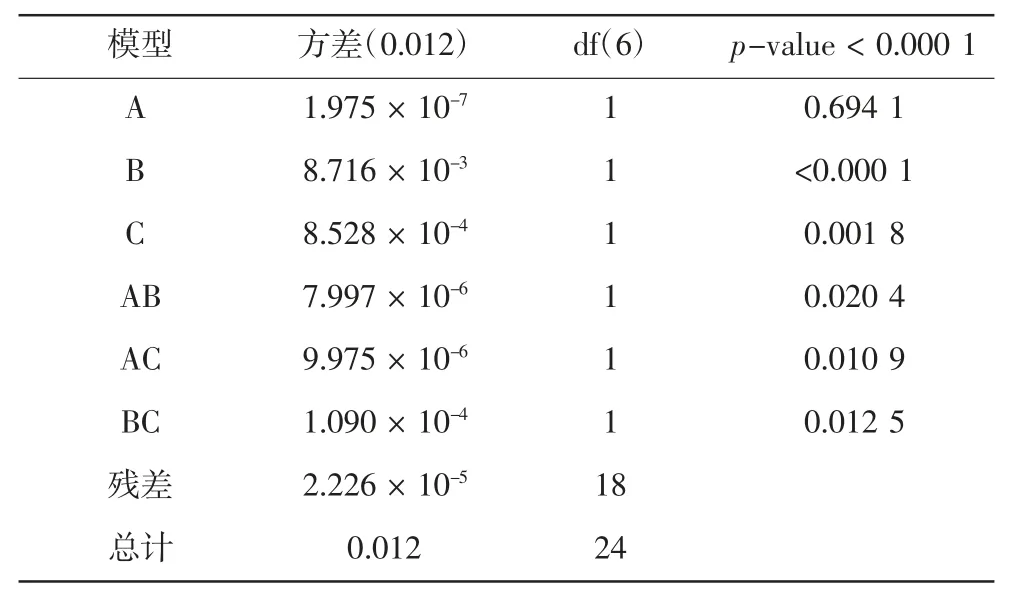
表5 流量方差分析Tab.5 Analysisofflowvariance
极差的计算过程与分析打击力时类似,流量试验方差分析如表6所示。由3个因素的极差,可以看出RB>RC>RA,因此各因素从主到次的顺序为:B(相贯深度)、C(出口扩张角)、A(收缩段角度),这也验证了前面依据p-value值所得出的结构参数对流量的影响大小。
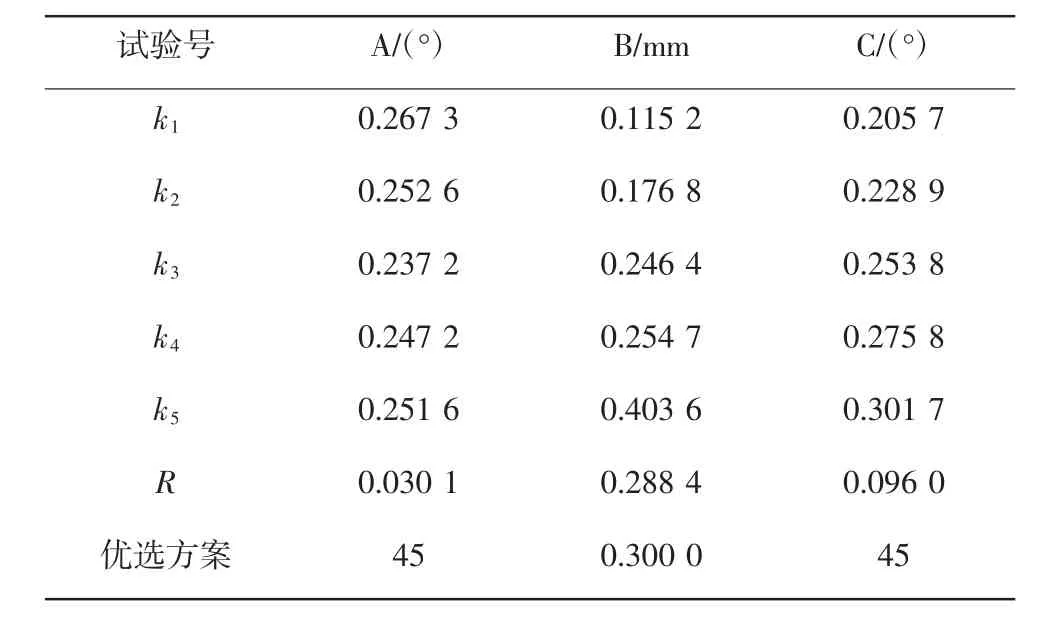
表6 流量试验方差分析Tab.6 Flowtestvarianceanalysis
对于流量来说,显然方差越小越好,所以应选取每个因素的k1,k2,k3,k4,k5中最小值对应的水平,显然,对于因素A来说,水平3是最好的,即收缩段角度应选取45°;对于因素B来说,水平1是最好的,即相贯深度应选取0.30mm;对于因素C来说,水平1是最好的,即出口扩张角应选取45°。
2.3.3 多指标试验择优方案
对于该问题,衡量清洗效果优劣的指标出现了两个,导致该问题产生了一定的复杂性,表现在这两个指标之间出现了相互矛盾的现象,选择一个指标好的水平组合对另一个指标来讲可能是不好的,例如大的相贯深度对打击力是择优而选,但对流量这个评价指标就算是一个劣势选择。该问题中,所选取的打击力优选方案对于流量并非优选方案,这时就需要兼顾各个指标,寻找使得每个指标都尽可能好的生产条件。为解决这个问题,可依据综合评价的准则进行综合平衡。
收缩段角度A:对于打击力和流量来讲,A对试验结果的影响较小,因此对于A指标的选取可依据显著性的大小。对于打击力,A的p-value为0.0766;对于流量,A的p-value为0.6941,而pvalue越小,表明该指标对结果影响越显著。因此,这里依据对打击力的影响来选取指标,选取水平1,即收缩段角度应选取30°。
相贯深度B:对于打击力来讲,B的极差最大,是影响最大的因素,取最大值的水平,即水平4最好;但对于流量来讲,B也是影响最大的因素,但评价指标是越小越好,需要选取最小值的水平,即水平1最好,这两者之间相互矛盾,洗扫车在清洗过程中,清洁率占优先地位,若是不能将地面清洗干净,则说明该产品并不合格。根据综合平衡法的原则,这时候应满足相对重要的指标,以打击力优先,选取水平4,即相贯深度为0.6mm。
出口扩张角C:对于打击力和流量来讲,C是对两者影响较为重要的因素,这里依据C指标显著性的大小选取,对于打击力,A的p-value为0.0011;对于流量,A的p-value小于0.0001,可依据对流量的影响来选取指标,这样也可在满足较大打击力的情况下,做到尽可能地节省水资源,降低损耗,因此,选取水平1,即出口扩张角应选取45°。
综上所述,对于该类型的扇形喷嘴,收缩段角度应选取30°,相贯深度为0.60mm,出口扩张角应选取45°。
3 优化结果的仿真分析及验证
3.1 喷嘴结构的有限元仿真
使用三维建模软件UG建立扇形喷嘴的三维模型及外流域场,如图3所示。喷嘴的端面为水流入口,大圆柱的端面作为水射流打向的靶面,将建立好的模型导入到ICEM CFD流体网格划分软件中,由于喷嘴相对于外流场尺寸较小,为了对扇形喷嘴的射流流场准确地仿真模拟,特对扇形喷嘴的内部流道进行了网格局部加密处理,对模型分3部分进行网格划分,喷嘴和外流场部分采用六面体单元,喷嘴与外流场交接处的三棱柱部分采用正四面体单元,交界面处进行节点合并,扇形喷嘴及外流场网格如图4所示。使用有限元软件Fluent模拟水流从喷嘴进入到打向地面的这一过程,扇形喷嘴的端面为压力进口边界条件,压力值设为6 MPa;扇形喷嘴的内表面采用壁面条件;外部流场区域设为压力出口边界条件,压力值为1个标准大气压。湍流模型采用k-ε两方程模型,计算过程采用VOF两相流模型模拟气液两相流作用,主项设为水,第二项为空气。
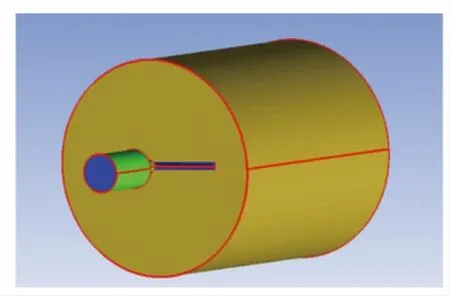
图3 扇形喷嘴的三维模型及外流域场Fig.3 Three dimensional model of fan-shaped nozzle and drainage field

图4 扇形喷嘴及外流场网格Fig.4 Grid diagram of sector nozzle and outflow field
3.2 打击力及流量分析
喷嘴原结构中收缩段角度α=45°、相贯深度h=0.5 mm、出口扩张角θ=45°,经过Fluent的迭代求解,得到原扇形喷嘴中面处的速度云图和优化后喷嘴中面处的速度云图,分别如图5和图6所示。
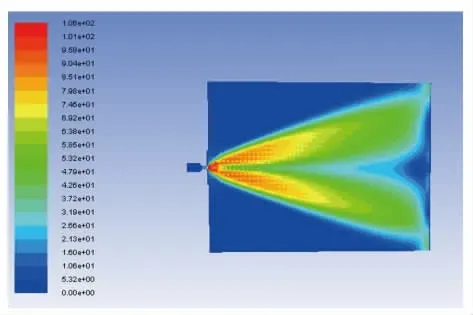
图5 原扇形喷嘴中面处的速度云图Fig.5 Velocity nephogram in the middle of the original sector nozzle

图6 优化后喷嘴中面处的速度云图Fig.6 Velocity nephogram at the middle surface of optimized nozzle
高压水从喷嘴喷出后,逐渐形成扁平状的扇形流束。在水射流范围内存在射流核心区,射流核心区内射流水的速度最大,对清洗表面的冲击力最大,喷嘴清洗的效果最为显著。同时在射流的纵向区域内,水射流的速度分布均匀。同样对优化后的喷嘴模型进行有限元仿真。根据后处理的结果,查看喷嘴靶面的打击力以及喷嘴出口处的质量流量,分别如表7和表8所示。

表7 喷嘴靶面的打击力Tab.7 Strike force of nozzle target
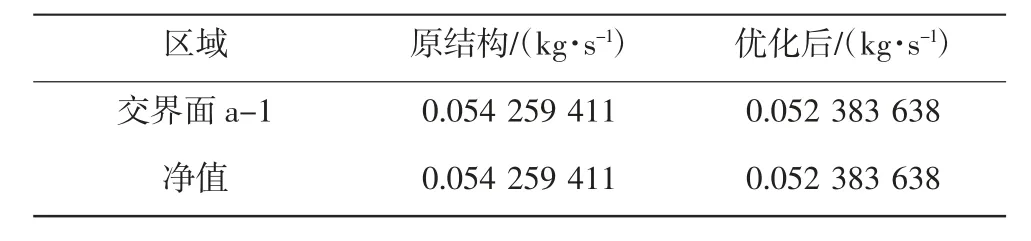
表8 喷嘴出口处的质量流量Tab.8 Mass flow at nozzle outlet
对比原喷嘴结构和优化后喷嘴结构的仿真结果可知,优化后的喷嘴在相同的入口压力条件下,射流速度更大,在打击力提高的情况下,流量也有一定的减小,打击力相较原结构提升了13.5%,流量相较原结构减小了3.7%,作业效率和清洗效率都有了一定的提升。
4 结论
文中以某重工所生产的系列洗扫车上水力系统的执行元件——扇形喷嘴为研究对象,运用正交试验法进行多目标优化设计,研究了某型号扇形喷嘴的结构参数的变化对其射流性能的影响,提出了一套系统研究扇形喷嘴的结构参数优化的分析设计方法。本文对收缩段角度、相贯深度和出口扩张角3个扇形喷嘴的结构参数进行了优化,发现相贯深度对打击力和流量影响最大。根据综合平衡法的原则,以打击力优先考虑的因素,通过正交试验设计得出,当收缩段角度是30°、相贯深度为0.60 mm,出口扩张角为45°时可获得最佳的打击力,且质量流量也在一定程度上有所减小。仿真分析结果验证了优化设计结果的有效性。该方法也为洗扫车其他型号喷嘴的优化设计提供了理论指导。

