锂电池能量状态与功率状态的联合估计

范汝新，张宵洋，张振福，毛顺永

(山东科技大学海洋科学与工程学院，山东青岛266590)

SOE是电池组实时剩余可用能量状态；SOP是电池组峰值功率状态，是在预定时间间隔内电池所能释放或吸收的最大功率。准确估算SOE和SOP有利于电动汽车稳定可靠运行。

安时积分法的电池荷电状态(SOC)是对电流的线性积分，只是描述了电池的剩余容量状态信息，事实上并不能将SOC等同于SOE。而SOE不但包含了电流变化信息，还充分考虑了电池工作过程中电压的变化。功率积分法是对SOE的标准定义，也是SOE最基本的估计方法，即在有限时间内对电池电压与电流的积分[1]。然而，由于电流或电压传感器的测量噪声以及直流漂移，易导致误差积累现象，并且严重受初始值准确性的影响。文献[2]通过大量的测试数据描述了开路电压(OCV)、SOE与电池能量之间的关系，并采用查表法的形式将其存储在电池管理系统中。文献[3]分析了不同温度和不同老化程度下的电池数据。文献[4-5]介绍了采用神经网络算法来化简电池工作过程中电化学反应的复杂机理的方法，该方法是开环方法。它依赖数据的测量精度，需要训练大量参数，估算结果受参数规模和训练方法的制约。文献[6]基于双极化模型和扩展卡尔曼滤波算法估计了SOE，但是精度一般。文献[7]考虑了电池老化对SOE的影响，并将开路电压拟合成关于老化和SOE的函数，然后运用了自适应无迹卡尔曼滤波算法进行SOE估计。尽管卡尔曼滤波及其衍生算法能够实现较好的效果，但是它们依然只适用于高斯白噪声的条件。文献[8]建立SOC和SOE之间定量关系，解决了SOE估计算法复杂度和精度之间的矛盾。但该方法忽略了内阻耗能，仅适用于小倍率电流条件。

SOP估计方法通常分为插值法[9]、模型法[10]和数据驱动法[11]。HPPC 插值法是在电池测试过程中离线标定不同SOC、温度和老化的峰值功率，得到峰值功率的解析公式或多维图。虽然这种方法原理简单可靠，但是该方法需要做大量的实验来提前测试标定，再将其存储在电池管理系统中，并且其动态特性较差[12-13]。基于BP 神经网络等数据驱动的方法需要将影响量作为输入，通过大量的训练数据来获得SOP的实时估计[14]。虽然该方法具有较高的精度，但是计算量大、计算复杂的问题也难以避免。模型法需要考虑电流、电压、SOC和温度等限制条件对SOP的影响。文献[10]提出的基于Rint 模型的方法的估计精度较低，并且不能用于估计持续功率。近年来，一阶RC 模型[11]和改进的RC 模型[12]等多种模型被用来估计动态条件下的SOP，以获得更高的估计精度。在电池限制条件的选择上，单独使用基于SOC的方法会造成估计峰值电流过大，存在安全隐患问题。文献[13]同时考虑多重限制条件。但是以上基于模型法的研究都没有考虑SOE对持续SOP估计的约束影响，实际上，SOE相比SOC能反映的电池状态信息更加全面。如果单独估计SOP和SOE，模型计算和模型参数辨识就成为一项重复的任务。因此，SOE和SOP的联合估计是提高估计精度的主要途径。

基于上述研究现状，本文采用扩展卡尔曼粒子滤波算法(EPF)估计SOE，以提高SOE的估计精度和对噪声影响的鲁棒性。另外，为了避免单独估计SOE和SOP的模型辨识重复性，结合SOE的估计结果，在端电压、SOE和电池自身设计的多约束条件下实现对持续峰值SOP的联合估计。本研究有利于提高电池多状态联合估计的精度和鲁棒性，改善电池管理系统的可靠性。

1 锂电池等效电路模型

1.1 SOE 的定义

功率积分法是在已知SOE初值的前提下，通过对端电压与电流乘积累计求得当前的能量，进而实现当前状态SOE的计算，其表达式为:

式中：SOE0为电池能量状态的初始值；η1为充放电效率；En为额定能量；I为电池负载电流；Ut为电池端电压。

1.2 等效模型

锂电池在放电静置过程中，对外表现出回弹电压特性。RC 环能够充分体现电池的极化效应，理论上RC 网络的阶次越高，对电池的外特性描述越符合电池的实际工作情况，但参数辨识就会越复杂，并且还会增加SOC估计的计算量。文献[15]测试了多种等效模型，指出二阶RC 模型表现最佳，对此建模如图1所示。

根据基尔霍夫定律，可得电池模型的连续状态空间方程：

式中：R0为欧姆内阻；R1、R2为电化学极化内阻；C1、C2为浓差极化电容；U1、U2为两个RC 环的电压；OCV为开路电压；Ut为端电压。

将连续状态方程离散化为：

采用HPPC 放电制度对锂电池进行实验测试，然后运用脉冲过程法进行离线辨识，相应的辨识结果如表1所示。

表1 锂电池等效模型参数

1.3 OCV-SOE非线性关系

OCV-SOE和OCV-SOC关系相关数据的获取采取小电流插值法，如图2所示。由图可以看出，开路电压相同时SOE与SOC却不相同，说明了两者存在差异并不能完全等效。

图2 开路电压和SOE以及SOC的非线性曲线

其中六阶多项式拟合相对来说能够准确地体现OCVSOE的非线性特性，如式(5)所示：

式中：z为SOE；a1= -6.502；a2= 34.65；a3= -69.48；a4=67.95；a5= -33.22；a6= 7.921；a7= 2.875。

2 基于扩展卡尔曼粒子滤波算法估计SOE

与扩展卡尔曼滤波算法(EFK)相比，粒子滤波算法(PF)的优点在于既不需要忽略泰勒展开式高阶项，也不会受到噪声分布的影响，但是粒子滤波算法在运行过程中会存在粒子退化的问题。因此本文将EKF 作为PF 算法的建议分布函数，即扩展卡尔曼粒子滤波算法(EPF)。

根据式(3)，对于锂电池的状态方程和测量方程可统一表示为：

EPF 算法的具体步骤包括七步：

3 多约束条件下的持续峰值SOP 估计

持续峰值SOP主要受当前端电压值、当前SOE大小以及电池本身的设计限值三种条件共同限制，若仅在单一限制条件下将会导致误差过大。

3.1 端电压约束条件

3.2 SOE 约束条件

锂电池的SOE需要满足一定的限制条件，即SOEmin≤SOE≤SOEmax。那么在当前时刻SOE的限制条件下，未来时间段L×T的持续峰值放电电流和持续峰值充电电流可分别表示为：

3.3 峰值电流和峰值功率

结合上述两种限制条件并同时考虑电池本身设计限制(放电峰值电流Idis和充电峰值电流Ich)，如表2所示，可分别得到多约束条件下的持续放电峰值电流与持续充电峰值电流。

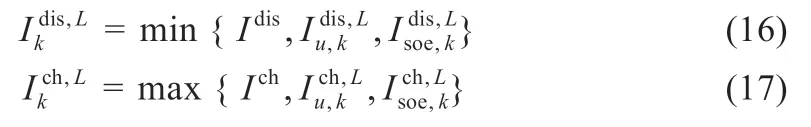
表2 锂电池充电和放电极值条件

结合式(10)可以分别得到持续峰值放电功率与持续峰值充电功率：

4 仿真测试结果分析

本文所用单体锂电池的额定能量为6.858 Wh，额定容量为2.1 Ah，截止电压为4.2 V/2.75 V，标称电压为3.7 V。

本文所提出的锂电池SOE和多约束条件下持续峰值SOP联合估计算法的具体实现步骤如下所示：

(1)对锂电池特性进行实验测试，得到动态应力工况(DST)的真实电流、电压和SOE数据，然后离线辨识模型参数；

(2)在Matlab/Simulink 环境下，将上述电压、电流数据注入到EPF 算法中以估计SOE值；

(3)运用上述多约束条件和SOE的估计数据以进一步估计持续峰值电流和持续峰值功率。

4.1 SOE 估计测试结果

图3 是不同算法放电的电池SOE和端电压的测试结果。由图(a)和(b)可知，EKF 虽然收敛速度较快，但对于SOE的估计误差较大，最大估计误差为6.29%。而PF 算法SOE的估计误差小于2%，即使存在初始误差，PF 算法仍然能够及时跟踪并稳定收敛，平均估计误差仅为1.7%。并且PF 算法能够解决EKF 算法仅适用于高斯白噪声条件的问题。EPF 不但比EKF和PF 的估计精度高，而且具有很快的收敛速度，也解决了PF算法粒子退化的问题。三种算法的最大绝对值误差、平均绝对值误差和方差的比较结果如表3所示，其中EFK、PF 和EPF的最大绝对值误差分别为6.29%、1.7%和0.013 2%，EFK、PF和EPF的方差分别为0.027 7%、0.001 7%、6.94×10-8%。

图3 DST工况下放电的测试结果

表4 不同算法对于SOE 估计精度的比较 %

端电压观测值始终跟踪于真实值，且EPF 的估测误差比PF 的更小，有效保证了算法对于状态变量的准确估计。另外，实际上过多的粒子对于降低估计误差的效果并不显著，反而会增加计算量和计算时间。经过多次测试，本文最终采用的是100 个粒子。

4.2 持续峰值电流估计测试结果

5、20 和60 s 下的持续峰值放电电流如图4(a)所示。持续峰值放电电流可分为三个阶段：第一阶段在高SOE区间，是由锂电池本身最大放电电流决定；第二阶段在中SOE区间，主要由端电压限制条件决定；第三阶段为低SOE区间，主要是由当前SOE限制条件决定，这是由于当锂电池实际的SOE值过低时甚至接近SOE限制条件时，基于SOE值的峰值电流估计条件将会降低放电的电流，避免对锂电池过放电。

持续放电的时间越长，第一阶段的时间就越短，越容易进入第二阶段。这是由于在相同放电电流下，放电时间越长，锂电池就会越容易达到截止电压。由于本文所采用的18650 型号锂电池自身设计条件的电流限制值实际较大，所以在高SOE区域的约束效果并不明显。就测试结果整体来说，在电池放电的前中期主要受端电压的限制条件的影响，持续峰值电流的整体走势较缓，而在电池放电的后期主要受SOE的限制条件影响，持续峰值电流的整体走势变陡。

图4(b)为持续峰值充电电流的结果。持续充电的时间越长，第二阶段的长度就会越长。这是因为持续充电时间越长，同时刻要达到充电截止电压所需要充电的电流就越小，所需要的充电电流就会以更慢的速率达到电池设计最大充电电流，第二阶段就会越长。

图4 持续峰值电流

4.3 持续峰值功率估计测试结果

5、20 和60 s 持续放电时间的DST 工况下的持续峰值放电功率的曲线如图5(a)所示。持续峰值放电功率在三种持续时间下的整体走势基本一致，但纵向对比而言，持续放电的时间越长，同时刻的持续峰值放电功率越低。这是因为持续时间越长，持续峰值放电电流会降低，端电压就会越低，从而使得持续峰值放电功率越低。

图5(b)是相应的持续峰值充电功率的结果。在第二和第三阶段中，持续充电时间越长，同时刻的持续峰值充电功率的数值越小。随着持续充电时间越长，同时刻要达到SOE充电限制条件或端电压充电截止条件所需要的充电电流就越小，持续峰值充电功率就越低。持续峰值充电功率的数值在第一阶段时会先增大，在后续阶段再减小。第一阶段中持续峰值充电电流为一个恒定值。随着动态工况的运行，电池的SOE和OCV逐渐减小，以恒定电流进行持续L×T时间充电后的端电压也逐渐减小，因此持续峰值充电功率数值逐渐减小。

5 结论

由于SOE的估计精度影响着持续峰值SOP是否可以准确估计，所以本文基于二阶RC 等效模型，运用了扩展卡尔曼粒子滤波算法来实时估计SOE，从而保证了SOE具有较低的估计误差。然后结合SOE的估计结果，在端电压、SOE和锂电池本身设计的多重限制条件下对持续峰值SOP进行了联合估计。DST 放电的测试结果表明了所提出联合估计算法的有效性和鲁棒性，并且具有较高的估计精度。另外，需充分考虑温度和老化对锂电池模型参数的影响才能更充分地表达锂电池系统复杂的等效机理，这是后续的研究重点。