钢-聚丙烯纤维增强人造花岗岩机床立柱结构设计及其性能仿真*
乔雪涛 杨 泽 王 朋 李 放 周世涛
(中原工学院机电学院,河南 郑州 450007)
立柱是数控机床的关键基础件和导向元件,其静、动态特性直接影响到机床的加工精度。但现阶段立柱结构设计多采用传统的经验设计,材料多选择铸铁材料,无法实现立柱结构的轻量化、高稳定性。采用新型结构和新型材料成为提高立柱静动态特性、高稳定性和抗振的有效手段之一。近年来,国内外学者深入研究了碳纤维、玻璃纤维、钢纤维、玄武岩纤维以及钼纤维作为增强相增强树脂基混凝土的新材料代替传统混凝土材料应用于机床基础件的可能性[1-6],虽然混杂纤维混凝土相对于未添加纤维混凝土的力学性能有所提升,但相对于数控机床而言仍有所不足。于英华等人为改善机床稳定性、可靠性将玄武岩纤维应用于机床基础件,同时采用遗传算法对机床基础件结构尺寸进行最优化设计,优化后性能有所提升,但是并未对机床基础件材料体积分配进行拓扑优化获取最佳材料分配布局[7-8]。刘江等人基于能量平衡原理来改善机床结构动态特性,优化后的仿真结果表明结构动态特性得到了提升[9]。Twu M J采用先进优化算法对机床结构进行优化,优化结果表明机床性能有所提升,但是其并未将新材料与优化算法相结合同时应用于机床基础件上[10]。Wang Y X 等人采用有限元法中模态分析获取了机床立柱的前20阶频率,基于模态分析对机床立柱的结构进行改进,提高了机床整体的动态性能[11]。黄华等人提出了一种混凝土与铸铁材料结合使用的新型床身结构设计,仿真结果表明组合材料床身的静刚度与纯铸铁床身基本相同,但动态性能有着显著提升[12]。Sun P C采用多目标优化方法针对机床结构中的元结构进行优化,其不足之处在于只是单纯改善了以经验法设计的元结构尺寸[13]。钢-聚丙烯纤维增强人造花岗岩(steel-polypropylene fiber reinforced synthetic granite,SPFG)通过在人造花岗岩中按一定配比加入钢纤维与聚丙烯纤维制备而成,钢-聚丙烯纤维增强人造花岗岩融合了钢纤维的高初裂强度、高模量以及聚丙烯纤维高韧性和抗冲击性[14]。本文研究钢-聚丙烯纤维增强人造花岗岩机床立柱结构设计及其性能仿真,为下一步SPFG材料在机床基础部件中的应用提供参考。
1 SPFG机床立柱结构设计
以某数控机床立柱为新型机床立柱的设计原型,主要设计参数及横截面尺寸如图1及表1,材料为铸铁[15]。

钢-聚丙烯纤维增强人造花岗岩相对于铸铁具有高阻尼、小振动和热稳定性好等特性,但是其抗压、抗弯等静态特性相对于铸铁较低,因此采用等价断面设计原则将SPFG材料立柱初步设计为矩形空心梁结构,主要设计参数及其横截面尺寸参照图2及表1。
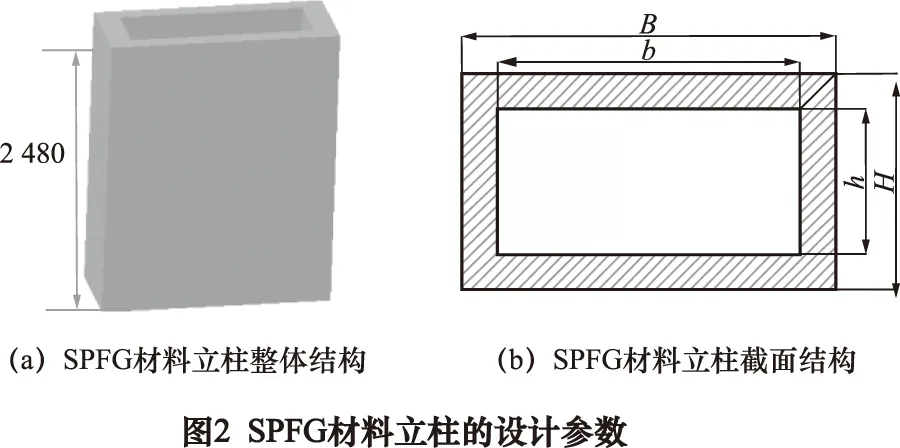
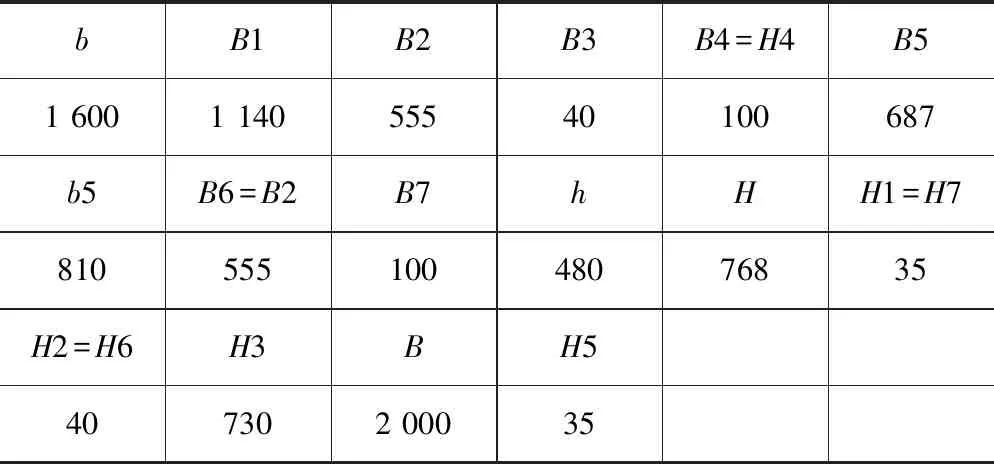
表1 原型铸铁立柱与SPFG材料立柱的关键参数
分别计算铸铁立柱与SPFG材料立柱的轴惯性矩,惯性矩是反映截面抗弯特性的一个量[16]。首先将铸铁立柱划分为图3所示的7个部分截面,然后运用平移轴定理分别计算上述截面的轴惯性矩,计算之和即为铸铁立柱的总惯性矩。
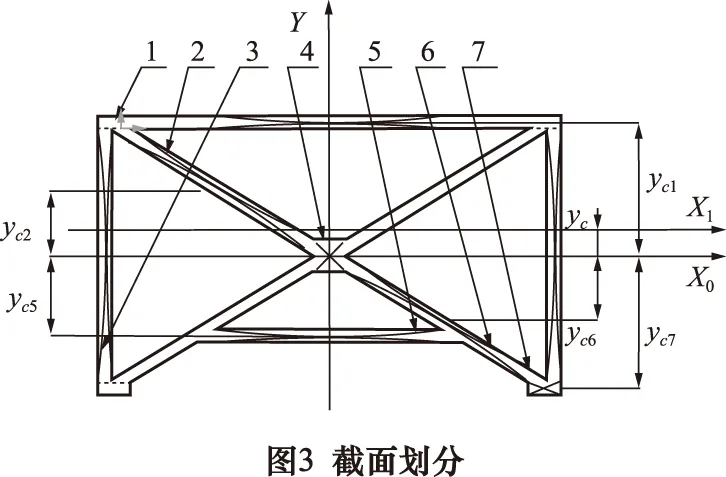
Tc=T1c+2T2c+T3c+2T4c+T5c+2T6c+2T7c
(1)
T5c=T5x+A5(yc5-yc)2
(yc5-yc)2
(3)
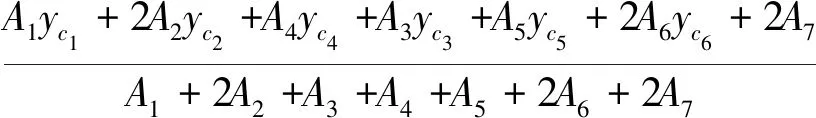
(4)
式中:yc为原型铸铁立柱截面形心距,mm;Tix为第i部分截面对坐标轴X0的惯性矩,mm4;Ai为第i部分截面的面积,mm2;yci为第i部分截面的中心距,mm;Tic为第i部分截面对形心轴X1的惯性距,mm4;i为1~7;其余为原型铸铁立柱截面主要尺寸。
因SPFG材料立柱截面为常见矩形截面不用重新划分截面,如图2b所示,因此可由表1中SPFG材料立柱截面尺寸计算出SPFG材料立柱截面的截面惯性矩TB为
(5)
式中:B、H、b、h为表1中SPFG截面尺寸。
经计算,在质量相等的情况下,铸铁立柱的抗弯刚度系数为1.963 N/m,SPFG材料立柱的抗弯刚度系数为2.673 N/m,提高了36.1%。
2 SPFG立柱的静态特性分析
2.1 立柱模型的建立
由Creo软件建立两种材料立柱的三维模型,并赋予如表2所示的材料属性[14]。
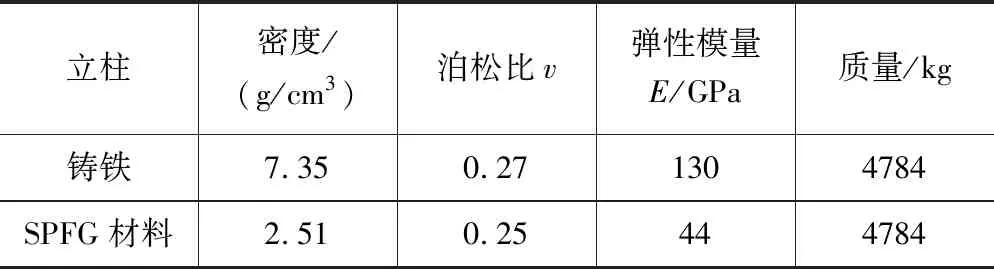
表2 两种立柱的材料属性
2.2 网格划分
对两种立柱的划分均采用20 mm网格划分,原型铸铁立柱模型划分后得到490 064个节点,92 132个单元。SPFG材料立柱模型划分后得到1 052 080个节点,238 576个单元。
2.3 边界载荷设置
因机床立柱上方垂直刀架和导轨横梁的作用,分别在立柱顶端施加垂直向下大小为0.05 MPa均布面载荷、导轨面上施加0.08 MPa水平分布面载荷,以及自身所受重力和立柱底部的固定约束,两种材料立柱所受载荷大小及约束类型一致。
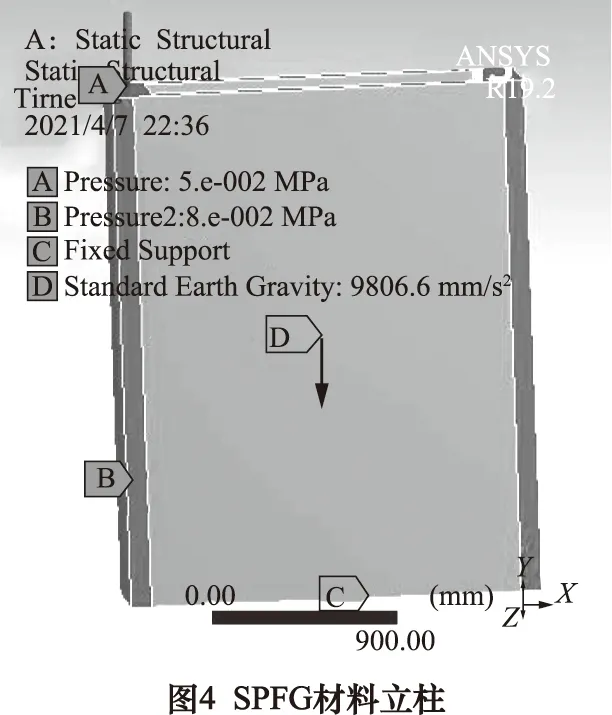
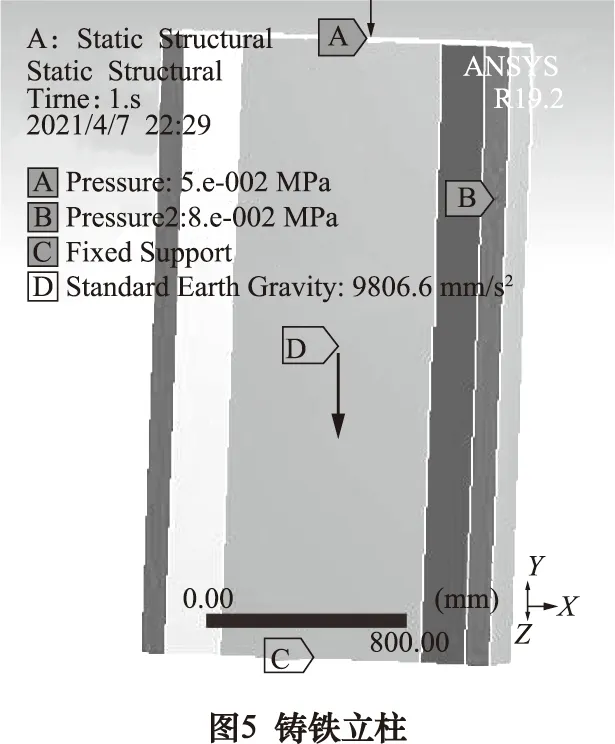
2.4 结果分析
在经过上述网格划分、边界载荷设置后,可得到两种立柱的应力和位移云图如图6、图7所示。


由图6、图7可知,在质量相同的情况下,铸铁立柱最大应力为2.5 MPa,SPFG材料立柱的最大应力为0.73 MPa,减小了70.8%;铸铁立柱的变形位移为0.061 mm,SPFG材料立柱的变形位移为0.046 mm,减少了25.5%。SPFG材料立柱的静态特性优于铸铁立柱。
3 SPFG立柱的动态特性分析
3.1 模态分析
通过模态分析可以得到机床立柱前六阶的固有频率及振型,下面使用Workbench中的Model模块对两种立柱进行模态分析。由于其振型相同,所以只列出SPFG材料立柱前6阶模态振型图,如图8所示,以及2种立柱不同的固有频率,见表3。

表3 2种立柱的6阶固有频率 Hz
3.2 谐响应分析
使用Workbench谐响应模块进行分析,对两种立柱施加振幅为1 000 N,频率变化为0~400 Hz的外部激振力,同时选定迭代次数为20次,分别得到立柱在X、Y、Z方向上的振幅-频率图,如图9~11所示。
由图9~11可知,SPFG材料立柱在X、Y、Z方向的最大响应振幅比原型铸铁立柱分别减小了91%、80%、63%。


4 SPFG立柱结构优化
4.1 拓扑优化
为满足轻量化的设计要求,在保持原有立柱的静动态性能情况下,以材料体积比为约束,以立柱的材料分布密度为设计变量,以结构柔度最小为设计目标的试验方案。通过Topological optimization模块,对立柱进行拓扑优化后处理,结果如图12所示。



4.2 尺寸优化
经拓扑优化后,SPFG材料立柱具有较好的结构布局,再采用直接优化法对SPFG材料立柱的内部尺寸进行优化。
4.2.1 基于Neural Network函数法的响应面模型
借助于Creo软件构建立柱参数化模型,如图13所示。并通过中心响应复合试验(central composite design,CCD)建立响应面模型[17],试验点及其数据如表4所示。
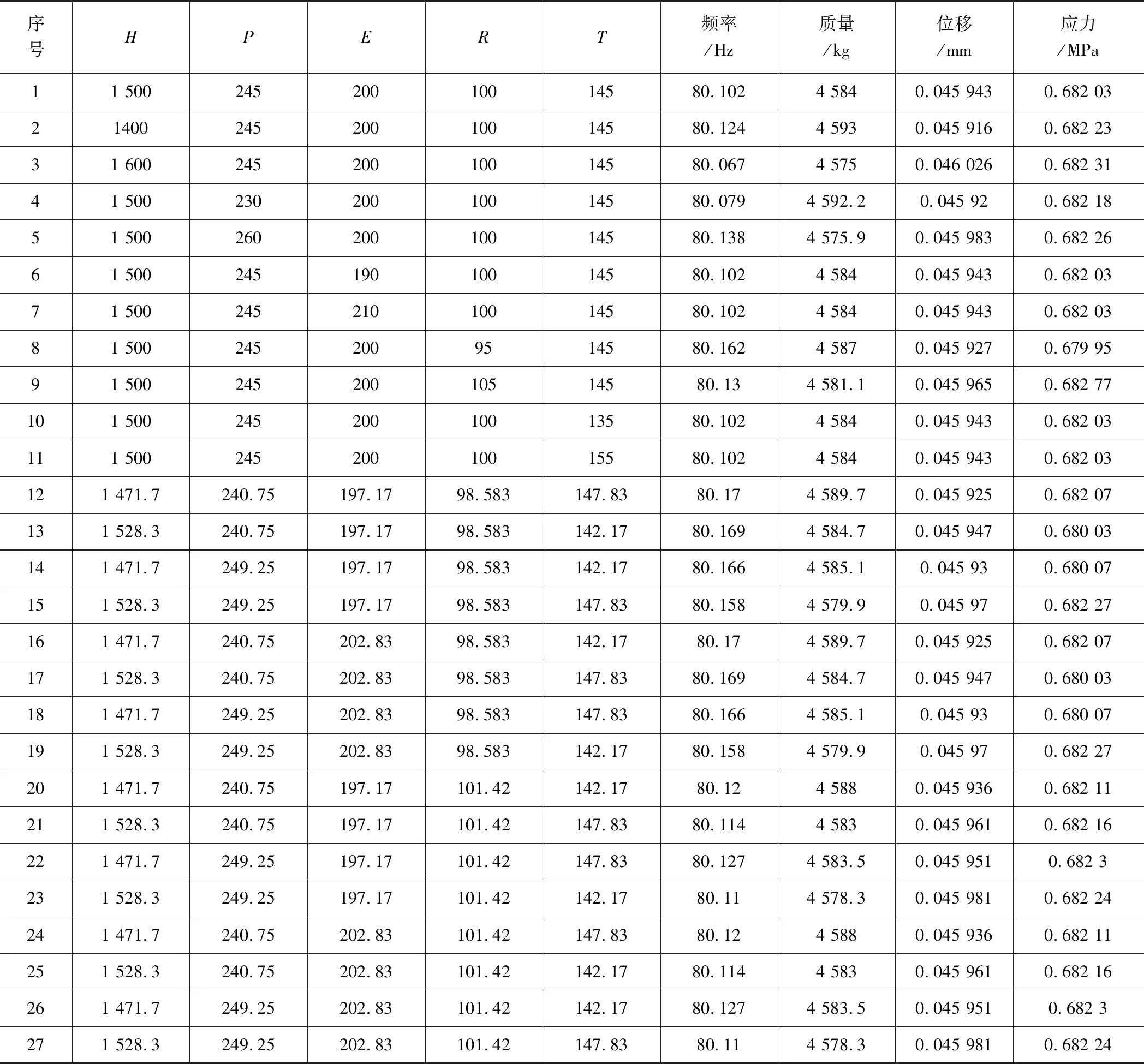
表4 CCD试验点及其数据

对Neural Network(神经网络)函数响应面模型的拟合度曲线的求解,神经元细胞个数对模型精度有很大影响[18]。基于公式(6)选定本模型神经元细胞数量为8(单元格数量区间为5~10),求解得如图14所示拟合度曲线。
(6)
式中:y为神经元细胞数量;m为输入层神经元数量为立柱的设计变量;n为输出层神经元数量为立柱的约束变量;a为取值范围0~10的常数。
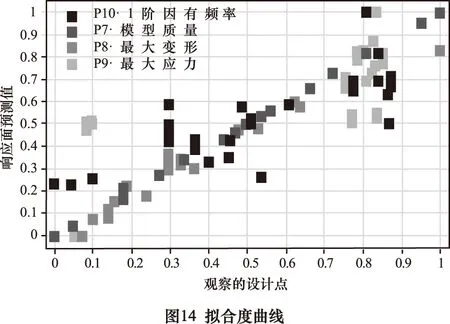
4.2.2 基于MISQP算法立柱的目标优化
以立柱质量为目标函数,立柱的变形位移、最大应力、1阶固有频率为约束函数,内部尺寸为自变量。差分方式设置为前向差分,迭代次数50次,筛选出最优的3组候选点,如图15所示。
4.3 立柱优化结果分析
经两级优化后,SPFG材料立柱材料分布发生改变,壁厚DS_T由145 mm增大为155 mm,拓扑结构三视图如图16所示。
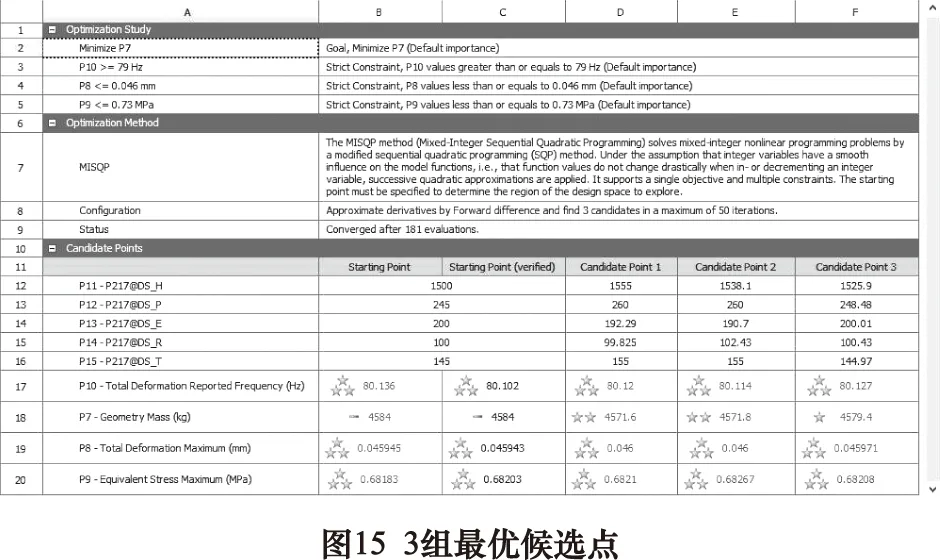
选取相同约束下目标函数最小的第1组尺寸与原型立柱进行相同边界条件下的静动态性能对比,可得到SPFG材料立柱相对于原型铸铁立柱静动态性能大幅度提升,具体参数如表5所示。

表5 立柱优化结果
经计算,2级优化后SPFG材料立柱的抗弯刚度系数为2.753 N/m,相对于未优化SPFG材料立柱的2.673 N/m提升了3%,但比原型铸铁立柱的1.963 N/m提升了40%。

5 结语
(1)在结构设计合理的情况下,SPFG材料立柱的抗弯刚度系数较同等质量的铸铁材料立柱提升了40%。
(2)经拓扑优化、尺寸优化2级综合优化,SPFG材料立柱较传统铸铁立柱质量减轻4.5%,最大应力减小72%,变形位移减小25%,1阶固有频率提升27%。
(3)经有限元分析与理论计算,二者结果基本一致,表明本文提出的结构优化设计方法是有效、可行的,采用SPFG材料制作机床立柱乃至其他机床基础件,可提高机床立柱及机床整体的静动态特性。

