F-P标准具结构设计及加工误差补偿方法研究
李 路,邢昆明,赵 明
(1.皖西学院 机械与车辆工程学院,安徽 六安 237012;2.中国科学院合肥物质科学研究院 大气光学重点实验室,安徽 合肥 230031)
Fabry-Perot(F-P)标准具是一种高精度光学仪器,可用于超精细结构的光学锁频、光学鉴频和光谱测量测量等高精度检测中。近年来,对F-P标准具的应用需求越来越大,已被广泛运用在测风激光雷达、星载云-气溶胶激光雷达、光纤通信、材料光谱测量以及高功率GHz窄线宽固态激光等超窄带光波滤波技术中[1-7]。F-P标准具可分为固态和气体标准具两大类。光束入射到标准具腔体后,在两个平行反射膜之间来回反射,形成多光束干涉效应,形成干涉仪。由于入射光束以不同波长通过标准具腔的相位厚度,可以实现不同波长的激光传输。随着涂层沉积技术的发展不断,固体标准具的应用技术也得到了研究人员的青睐。为了提高星载云气溶胶激光雷达的信噪比,固体标准具被用作窄带滤波器的核心部件532 nm探测通道,因此本文重点研究了标准具厚度制造误差对中心波长(532.12 nm)性能的影响,最后给出了标准具厚度误差补偿的定量计算结果。
1 F-P标准具滤波原理
两个互相平行的反射平面构成为常见F-P标准具,不考虑反射相移,设反射面振幅反射率分别为R1和R2,透射率分别T1和T2,之间的介质折射率为n,厚度为h。当两个面的反射率相等且透射率相等时,设R=R1=R2,T=T1=T2,则标准具透过率可简化为[8-9]:
其中,nh为标准具的光程;θ为入射角;λ为波长。
由上式,可以推导出F-P标准具的主要特征参数如下:
1)中心波长λ0
(3)
2)峰值透过率Tmax
在中心波长λ0处,可推导出:
(4)
3)半波宽FWHM
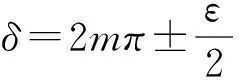
(5)

(6)
4)自由光谱范围FSR
(7)
5)精细因子Finesse
(8)
2 F-P标准具结构参数设计
2.1 标准具结构设计
根据项目设计要求,米散射激光雷达出射波长为532.12 nm,F-P标准具设计指标为FWHM为35±5 pm;自由光谱范围FSR为750±50 pm;折射率n0为1.461。通过公式计算出:反射率R约为 85%±1.4%;入射角为0时,F-P标准具厚度约为129.6±9 μm。本文所设计的F-P标准具中,取发射率R为85%;直径为30 mm。不考虑损耗时,在中心波长532.12 nm,计算出厚度与透过率曲线关系,如图1所示。由图1可知,随着厚度的变化,中心波长的透过率发生漂移,其规律如下:当F-P标准具中心波长为532.12 nm时,FSR为182.1 pm,FWHM为9.4 pm。在选择F-P标准具的厚度时,中心波长及折射率一定时,本文在中心波长为532.12 nm时,选择厚度为131.1179 μm。确定F-P标准具厚度后,在不考虑损耗的情况下,计算出不同波长与透过率曲线的关系,并获得主要性能参数,如图2所示。
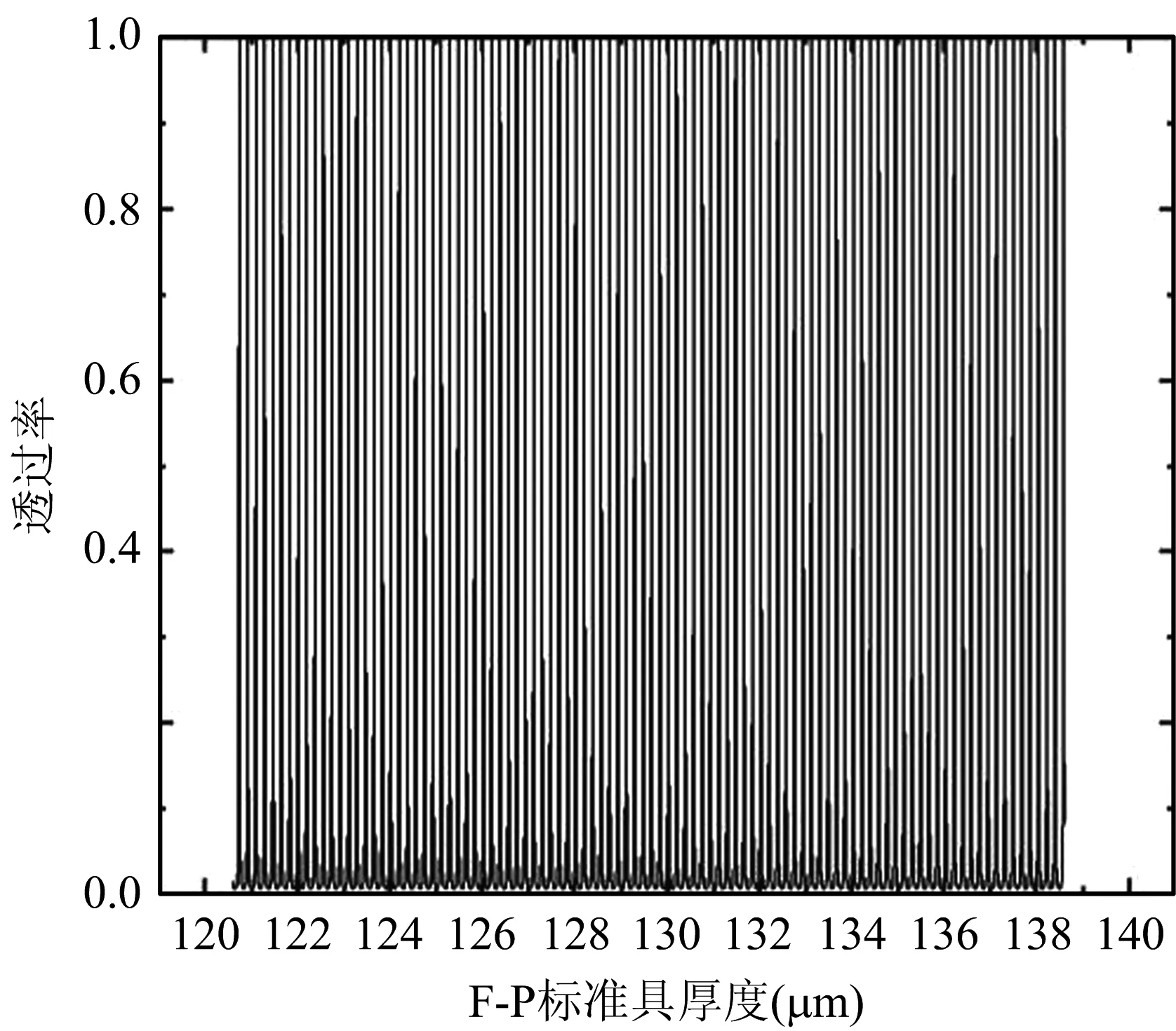
图1 F-P标准具厚度与透过率的关系曲线

图2 波长与透过率的关系曲线
由图2可知,在中心波长为532.12 nm时,F-P标准具厚度为131.1179 μm,FSR为738 pm,FWHM为38.2 pm,符合设计要求。由于设计的F-P标准具厚度相对于径向尺寸非常小,其结构强度不够,本文所设计的F-P标准具光学组件采用“夹层式结构”,即利用两个保护玻璃将F-P标准具夹在中间,增加其机械强度和光学面型,且保护玻璃外出涂有高透膜。这种结构简单,稳定性好,适用于星载激光雷达,如图3所示。

图3 F-P标准具光学组件
2.2 误差对F-P标准具滤波性能影响
在实际的加工过程及安装调试过程中,所选的标准具厚度存在误差,决定了中心波长的位置和透过率的大小。不考虑耗损的情况下,模拟了F-P标准具厚度误差对中心波长透过率大小的影响。当标准具厚度误差较大时,如图4所示,标准具厚度误差值以kλ0/2n(k为整数)变化时,中心波长的最大透过率值以λ0/2n为周期交替出现。当标准具厚度误差较小时,如图5所示,在中心波长为532.12 nm时,标准具厚度相对误差超过0.0133 μm时,透过率小于10%。由此可见,F-P标准具厚度误差需要控制在纳米量级,但实际加工过程很难确保其加工精度。如果将F-P标准具误差控制在微米量级时,需要对其进行补偿,校正中心波长达到最大透过率的位置。
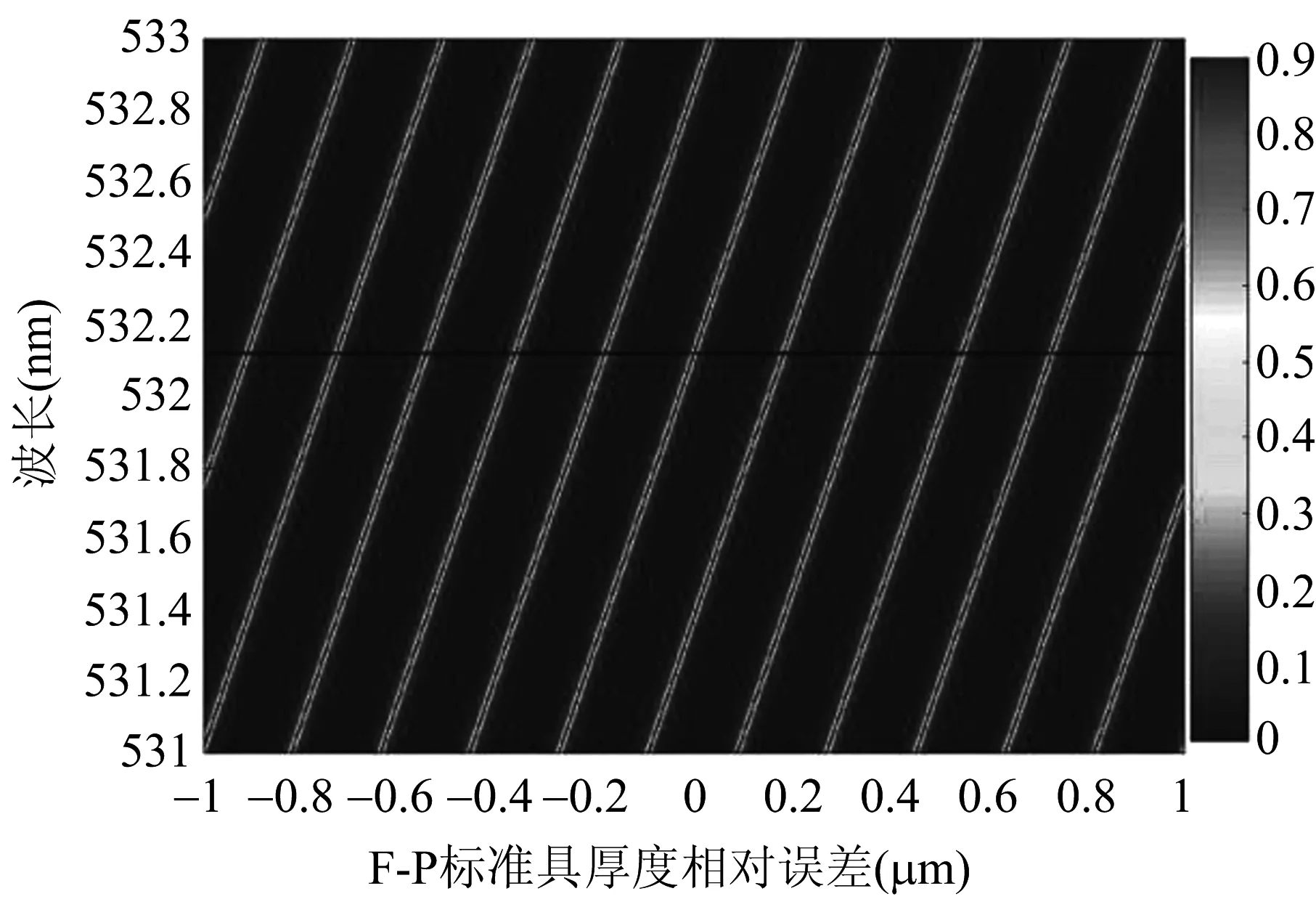
图4 F-P标准具厚度相对误差对中心波长附近光谱影响
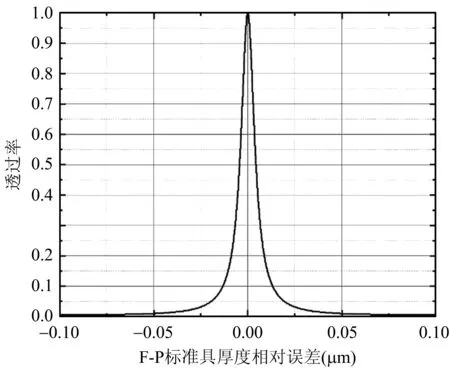
图5 F-P标准具厚度相对误差对中心波长透过率影响
最终设计出F-P标准具光学组件结构参数,如表1所示。
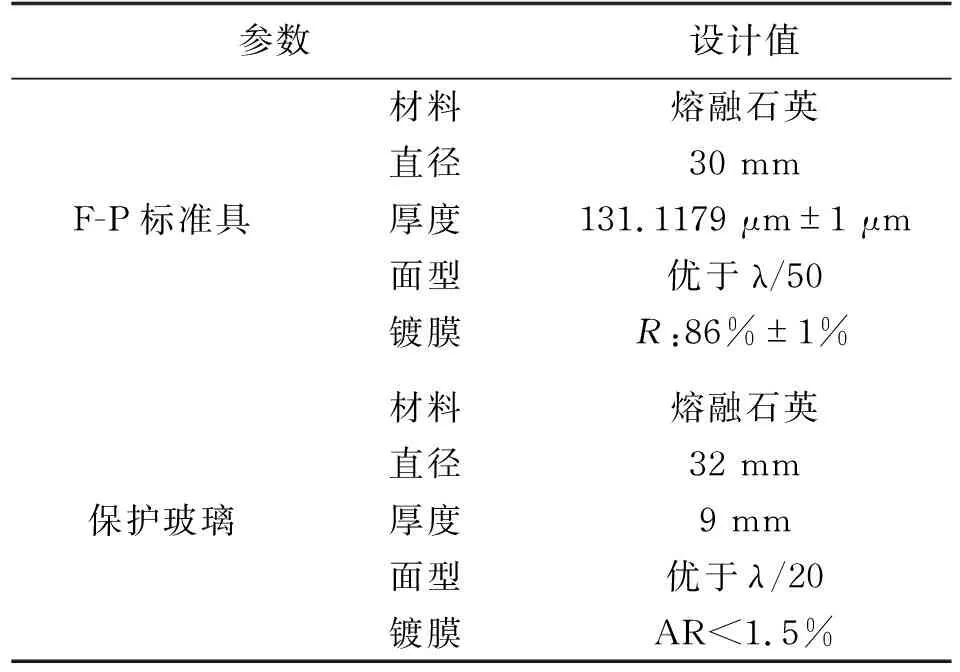
表1 F-P标准具光学组件结构参数
3 加工误差补偿方法
当F-P标准具厚度存在误差时,可通过改变其有效的光学厚度来实现中心波长调整到最大透过率的位置。显然,如果实现中心波长达到最大透过率的位置,需要将F-P标准具厚度在最大透过率的位置的光学厚度相对误差控制在纳米量级,但是精确测量这种纳米量级的厚度误差很难实现,因此选择间接等效补偿的方法对F-P标准具厚度进行补偿。目前,对于补偿方法的研究,主要由入射角度补偿和温度补偿两种方式。角度补偿主要通过改变FP标准具有效光程的方式进行补偿;温度补偿主要通过改变F-P标准具的折射率及几何厚度的方式进行补偿。随着温度的变化,F-P标准具的折射率及几何厚度变化关系式为:
(9)
上式中,h0为初始的标准具几何厚度;αt为线膨胀系数,为5×10-7/℃;βt为折射率温度系数,为10×10-6/℃;Δt=t-t0为温度变化值(t为工作温度;t0为参考温度)。
考虑入射角和温度因素的影响,将透过率公式变换为:
(10)
3.1 入射角补偿
F-P标准具厚度相对误差取值范围为-1~1 μm,入射角取值范围为0~50 mrad,在中心波长532.12 nm,模拟计算在不同误差下入射角补偿效应,如图6所示。从结果可知,入射角为0时,中心波长的最大透过率值以λ0/2n为周期交替出现。F-P标准具厚度正向误差和负向误差通过入射角补偿的角度不同的,即没有对称性。在同样的误差绝对值下,负向误差补偿角度大于正向误差补偿角。

图6 F-P标准具厚度相对误差与入射角匹配
3.2 温度补偿
假设F-P标准具厚度相对误差取值范围为-1~1 μm,取参考温度t0为22 ℃,工作温度取值范围为22~122 ℃,在中心波长532.12 nm,模拟计算在不同误差下温度补偿效应,如图7所示。从结果可知,工作温度为22 ℃时,中心波长的最大透过率值以λ0/2n为周期交替出现。F-P标准具厚度正向误差和负向误差通过入射角补偿的角度不同的,即没有对称性。

图7 F-P标准具厚度相对误差与温度匹配
4 结论
根据米散射激光雷达出射波长为532.12 nm对F-P标准具的滤波要求,确定F-P标准具的光学组件的结构参数。基于多光束干涉理论,深入研究F-P标准具的厚度加工误差对FP标准具滤波性能的影响,得出结论:厚度加工误差以kλ0/2n(k为整数)为周期变化时,可获得峰值透过率,无须补偿。厚度加工误差以一个周期内变化时,必须采用入射角或工作温度两种补偿方法,可高精度的定位由于加工误差带来的中心波长,实现高精度滤波。
5 感谢
感谢中国科学院合肥物质研究院大气光学重点实验室激光雷达研究室提供平台和数据支持。

