具有预先给定跟踪精度的机械臂固定时间控制
杨亚东,吴 健
(安庆师范大学 计算机与信息学院,安徽 安庆 246133)
近几年,有限时间控制因其具有高跟踪精度、快速响应和良好的抗干扰性能而受到越来越多的关注,并成为研究的热点[1-7]。文献[1]对有限时间控制的相关问题进行了综合性描述。有限时间控制的方法也逐渐被用于各种系统,包括航天器系统[2]、非仿射纯反馈系统[3]等。文献[4]研究了一类不确定仿射非线性系统的跟踪控制问题,提出了一种基于非对称模糊小脑模型干扰观测器的有限时间收敛backstepping控制策略。传统的有限时间控制方法,其驻留时间函数受系统初始状态的影响,阻碍了该方法的实际应用。
为了解决上述传统有限时间控制方法存在的缺陷,提出了一种新的有限时间控制方法,称之为固定时间控制,其优势在于驻留时间函数的上界与系统初始状态无关,只与设计参数有关。由于固定时间控制在理论和实践上的重要性,关于固定时间控制的研究成果不断涌现[8-12]。文献[8]针对多电机位置同步控制系统,提出一种自适应非奇异固定时间位置同步控制方法。文献[9]提出一种新的控制方法,将模型参数不确定及海洋扰动看作复合扰动,设计扰动观测器,实现固定时间内对扰动的精确估计。文献[10]针对不确定线性系统,提出了基于稳定多项式反馈的二阶滑模控制算法,确保控制系统是固定时间有界的。文献[11]研究了一类严格反馈非线性系统的固定时间跟踪控制问题。文献[12]针对具有自由滚转目标的航天器系统,提出了一种滑模流形控制方案,保证控制系统是固定时间稳定的。
随着科学技术的不断发展,机械臂系统被广泛地用于工业制造、医学治疗、娱乐服务、半导体制造以及太空探索等领域[13-20]。文献[13]基于backstepping控制策略和有限时间李雅普诺夫函数的方法,研究了机械臂的固定时间跟踪控制问题。在文献[17]中,提出了一种基于时变障碍李雅普诺夫函数的预设性能自适应控制方法,解决了带有输出约束的柔性关节机械臂的控制问题。
基于以上分析,本文研究一类单链路机械臂系统的固定时间控制问题。本文的主要工作如下:(1)针对单链路机械臂系统,提出具有预先给定跟踪精度性能的固定时间控制策略。(2)与文献[13]相比较,本文所提出的控制策略确保闭环系统均固定时间稳定,同时使系统的跟踪误差收敛于预先给定的精度。
1 问题描述及预备知识
1.1 系统描述
本文的研究对象为单链路机械臂,系统模型表示如下[13]:
(1)
其中θ(t)为角度,u(t)为输入扭矩,g为重力加速度,M为瞬时惯性,m为连杆质量,l为长度。
(2)
本文的控制目标是设计控制器u使机械臂角度y(t)在固定时间内跟踪上参考信号yr(t),且跟踪误差在固定的时间内渐近收敛于用户预先给定的区间。
注1 针对单链路机械臂系统(1),文献[13]提出了实际的固定时间跟踪控制策略,确保闭环信号在固定时间内收敛到原点的一个任意小的邻域内,但是该邻域的精确范围是无法预先确定的。为了解决这一问题,本文通过引入一类切换函数,构造新的类李雅普诺夫函数,提出一种新的固定时间控制方案,使得所有闭环信号是固定时间稳定的,且跟踪误差在固定的时间内渐近收敛于用户预先给定的区间。
为了设计出合适的控制器,相关的预备知识如下所示。
1.2 重要引理和假设
引理1[13]对于任意xi≥0和常数i=1,2,3,…,n,有
(3)
引理2[21]考虑系统
(4)
其中,x为状态变量,f(·)为连续光滑的函数,如果存在正定函数V(x),其导数满足:
(5)
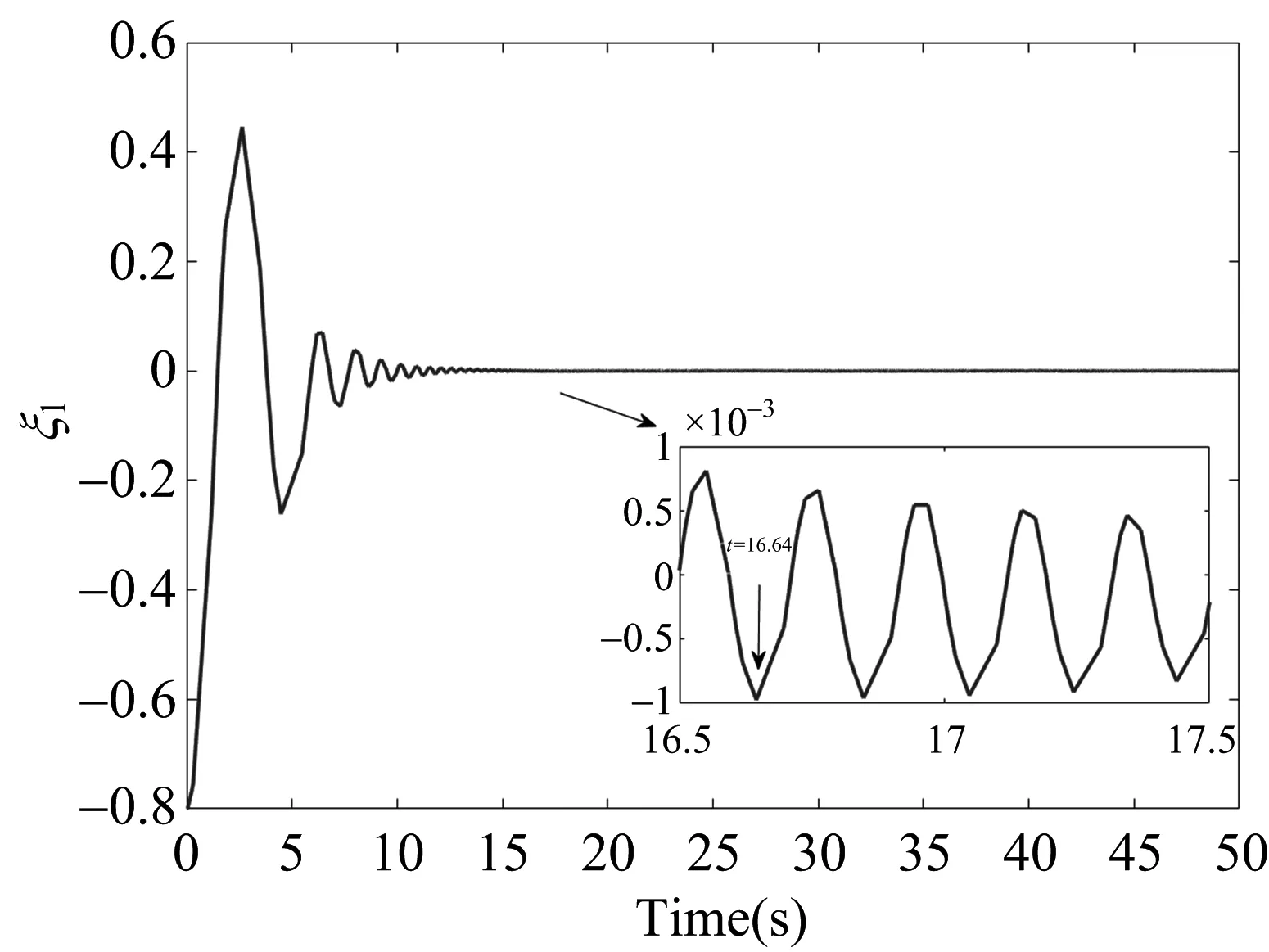
则系统(4)是固定时间稳定的,其中μ1,μ2>0,p>1,0 (6) 2.1 固定时间控制器设计 定义变量误差如下 ξ1=x1-yr (7) ξ2=x2-α (8) 其中α是虚拟控制器(15)。首先介绍如下两类切换函数[21] (9) 和 (10) 其中πi是设计参数,i=1,2。由(9)和(10),我们可以得到如下性质 (11) 基于反推法的设计过程如下 Step 1.由(2)和(7),我们可以得到 (12) 构造如下Lyapunov函数 (13) V1对时间t的导数如下 (14) 设计虚拟控制器α (15) 其中,a1和b1表示正的设计参数。于是可得 (16) Step 2.由(2)和(8),我们可以得到 (17) 构造Lyapunov函数如下 (18) 计算出V2的导数为 (19) 其中,控制器u设计为 (20) 式中,a2和b2表示正的设计参数, (21) 将(16)和(20)代入(19)中可得 (22) 式中 (23) 如果|ξ2|≤π2+1,则(|ξ1|-π1)φ1(|ξ2|-π2-1)≤0,所以ω≤0,如果|ξ2|>π2+1,则 (24) 即ω≤0。 将ω≤0代入(22)式可得, (25) 由引理1和引理2可得 将(26)和(27)代入(25)式,可得 (28) 注2 针对系统(1),文献[13]提出的实际固定时间跟踪控制策略,只能保证闭环信号在固定时间内收敛到原点的一个任意小的邻域内,但是其具体的收敛范围是无法确定的,也未给出具体收敛时间。本文提出的新的固定时间控制方案,不仅使得闭环信号在固定时间内稳定,而且保证误差在时间上限内收敛于预先给定的范围[-π1,π1]内。 2.2 稳定性分析 定理 1 针对系统(1),若假设1成立,基于构造的虚拟控制器(15)以及实际控制器(20),则在固定时间T0内 (1)所有闭环信号有界。 为了验证本文所提出的控制方案的可行性,利用MATLAB对系统(1)进行仿真,为了实现控制目标,选择设计参数如下a1=0.1,a2=0.2,b1=0.1,b2=0.2,π1=0.001,π2=0.2,g=9.8 m/s2,M=0.6,m=5 kg,l=1 m,系统初始状态x1(0)=x2(0)=0.2,参考轨迹yr=0.2sin(t)+cos(0.5t)。 仿真结果如图1~4所示,图1展示了系统输出y和参考轨迹yr,保持了良好的跟踪效果。图2给出了跟踪误差ξ1的时间轨迹,可以看出稳定后的跟踪误差在预定时间T0=16.64 s收敛于用户定义区间内,即|ξ1|≤0.001。图3 给出了响应曲线x1,x2。控制输入u如图4所示。 图1 系统输出y和参考轨迹yr(x1(0)=x2(0)=0.2,M=0.6) 图2 跟踪误差ξ1(x1(0)=x2(0)=0.2,M=0.6,π1=0.001) 图3 响应曲线x1,x2 图4 控制输入u 为了表明本控制方案的泛化能力,本文取值参考文献[13]中参数x1(0)=0.1,x2(0)=0.2,M=1, 实验结果如图5、图6所示,图5展示了系统输出y和参考轨迹yr,且依然能够保持良好的跟踪效果。图6给出了跟踪误差ξ1的时间轨迹,可以看出系统依然可以达到稳定状态。此外,我们将参数π1取值修改为0.1,实验结果如图7所示,闭环系统依然可以达到稳定状态,误差在预定时间内收敛于用户定义区间,即|ξ1|≤0.1。 图5 系统输出y和参考轨迹yr(x1(0)=0.1,x2(0)=0.2,M=1) 图6 跟踪误差ξ1(x1(0)=0.1,x2(0)=0.2,M=1,π1=0.001) 图7 跟踪误差ξ1(x1(0)=x2(0)=0.2,M=0.6,π1=0.1) 本文针对单链路机械臂系统,在反推控制策略和李雅普诺夫稳定性理论的基础上,通过引入一类切换函数,构造新的类李雅普诺夫函数,研究了系统(1)的固定时间跟踪控制问题。所提出的控制策略确保机械臂系统的输出信号在固定时间内跟踪上期望轨迹,并且跟踪误差收敛于用户预先定义的精度,并通过仿真验证了此方法的有效性。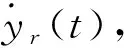
2 主要结果

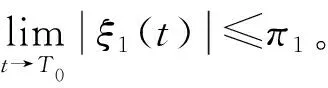
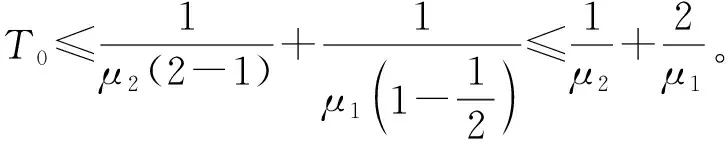
3 仿真与验证






4 结论

