一种基于均值法的无磁芯电流互感器设计及误差研究

项宇锴 郑茂华 吕阳星 吴勇海 曹沁婕

(国网龙岩供电公司，福建 龙岩 364000)

1 概述

基于磁传感技术的电流传感器因具有非接触测量、精度高、成本低等特点，广泛应用于电力电子系统中。在新能源系统中，如光电、风能、电动汽车等，基于磁传感技术的电流传感器使用量逐年增加[1-2]。

在过去的几十年里，霍尔电流传感器(Hall Current Transformer)已经在直流测量中广泛使用[3]。近年来随着新型磁阻传感器AMR元件[4]、GMR元件[5]、磁通门元件[6]和TMR元件[7]的发展，这些新技术因其高灵敏度和良好的线性度逐渐被应用于制作电流传感器。霍尔电流传感器灵敏度低、功耗高、线性度差等固有缺陷能够在这些新型磁阻传感器中被克服。在现有研究中，AMR的灵敏度远高于Hall，但线性范围较窄，并且基于AMR的磁传感器需要通过复位线圈进行复位操作，这导致了制造过程复杂。GMR的灵敏度也高于Hall，但线性范围同样较窄。此外，磁通门结构复杂且频率响应较低，不适用于成本低的高频响应系统。近年来，具有更高温度稳定性的TMR磁阻传感器被设计出来，相比于霍尔传感器具有灵敏度高、功耗低、线性度好、频率响应高等特点，被认为是具有前景的新一代磁场传感器。

在圆形传感器阵列的研究中，文献[8]提出采用印刷电路板(Printed Circuit Board,PCB)的设计来测量电流，并将传感器安装成圆形阵列 (近似于安培环分布)的设计有利于减少测量误差。文献[9]利用3个无磁芯霍尔传感器组成的阵列实现了0～10A电流值范围的测量，Mlejnek等对8个AMR传感器组成的圆形阵列进行了实验，实现了较高精度的测量[10]。而在上述方法中，载流导线须与圆形阵列平面保持垂直，且导线须被固定在圆形阵列的圆心。这些限制条件在工业应用中有许多不便之处，特别是在电力测量方面。

实践发现，当传感器被安装在PCB制成的圆形阵列时，均值法能够补偿因位置变化导致的测量误差，补偿效果取决于圆形阵列与载流导体的尺寸和位置信息。因此，本文的研究重点是基于圆形阵列均值法，关注圆形阵列与载流导线的位置关系，通过位置关系来评估载流导线的尺寸与圆形阵列的尺寸对测量误差的影响，在此基础上研究传感器数量(图1)对位置信息的抗干扰性，并希望抗干扰性研究能够给予工程人员在设计无磁芯电流传感器时提供参考。

图1 圆形阵列模型

本文首先对传感器与载流导线的位置关系进行数学建模，并选择圆形阵列的均值法来评估位置信息与传感器数量之间的关系。在实验过程中，将磁传感器安装在导体周围的PCB上，最后对实验结果进行讨论与总结。

2 载流导体的空间磁场分布

根据毕奥-萨伐尔定律，电流值不随时间而改变，电荷不会在任意位置累积或消失。采用国际单位制，用方程表示：

(1)

当载流导线为长直导线时，其磁感应强度BS可表示为：

(2)

其中，μ0为真空磁导率(μ0=4π×10-7A/m)，r为传感器与载流导体的最短距离，I为载流导体上流过的电流值，α为载流导体与圆形阵列平面的垂线(z轴)的倾角。根据式(2)，传感器感测得到的磁感应强度取决于载流导线和传感器的位置关系。

由图2可得，载流导体可以在圆形阵列内部发生倾斜和平移两种位置关系变化。由于机械结构的限制，其倾斜角无法一直增大，且当倾斜角逐渐增大时，平移的范围逐渐减小。因此，本文将最大倾角定义为αmax。

图2 载流导体与圆形阵列的位置关系

需要说明的是，圆形阵列上每个磁传感器感测的磁场强度是由载流导线上不同电流元产生的，这就导致圆形阵列上的每个磁传感器相对于导线的位置信息都是不同的。因此，本文采用向量法和数值法结合求解每个传感器感测到的磁场强度，如图3所示。

图3 传感器感测磁场值计算方法

测量误差δ表示为:

(3)

其中，Bavg为传感器感测磁场平均值，Br是无位置误差时的传感器感测得的磁感应强度。此外，各磁传感器根据等半径、等角度的原则平均安装于圆形阵列上，因此，每个传感器感测到的磁场值之间是存在一定联系的，其值变化与传感器阵列结构的设计是相关的。

3 位置关系对圆形阵列的影响

当载流导线存在倾角α时，交点在圆形阵列内的偏移区域将变为椭圆形。倾角较小时，载流导体在圆形阵列的移动范围如图4(a)所示；随着倾角逐渐增大，椭圆形的移动范围逐渐变窄，这使得载流导体在椭圆长边的移动位置受到限制，如图4(b)所示。因此，载流导体的移动范围可以被描述为：

图4 偏移系数范围

(4)

其中，kmax1为椭圆长边的偏移系数范围，kmax2为椭圆短边的偏移系数范围,D为载流导线的直径，R为圆形阵列的内径。ks为图4(b)载流导体在椭圆长边的移动范围，能够通过式(5)来求解。

可见，在满足αmax的情况下，载流导线的倾角α会影响kmax1和kmax2。为了更好地说明椭圆区域内各参数之间的关系，本文仿真了不同αmax下交点的可偏移区域，如图5所示。随着α增大，圆形阵列的偏移区域逐渐减少。可见，通过合理选择αmax能够限制kmax1和kmax2的范围。

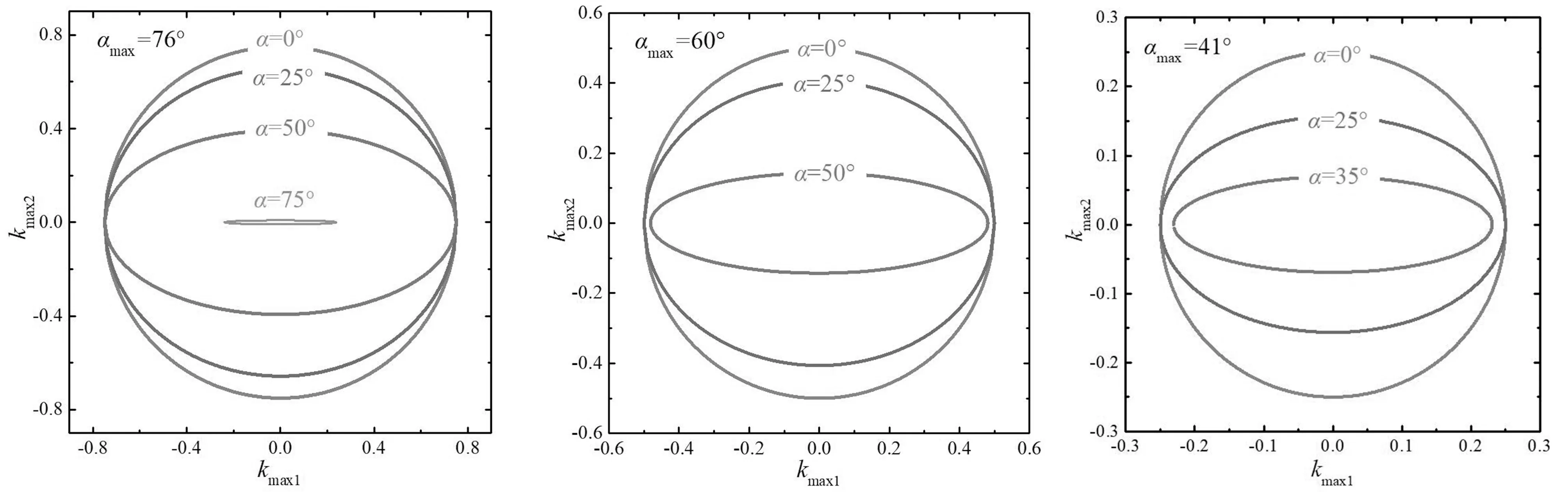
图5 交点偏移区域

(5)

4 仿真研究及硬件设计

4.1 仿真研究

上文分别揭示了当载流导体与圆形阵列平面的交点偏离圆形阵列圆心的情况和载流导线与圆形阵列垂线存在倾角情况下对测量误差的影响。但在工业应用中，两种情况是同时存在的。

测量误差δ受到各个位置因素的影响，各个位置因素之间又互相影响。αmax作为最大倾角，其限制了载流导体和圆形阵列之间的位置关系。因此，下文将探讨αmax对δ的影响。

图6 仿真算法

在Matlab计算软件上编写算法，用于分析αmax和δ的关系。在初始化阶段，n、δ将会被设置，并通过循环的方式，不断选择合适的αmax值带入，从而会获得偏移范围kmax1、kmax2，并在获得的范围内循环取值，从而得到多个传感器感测的磁场平均值Bavg与无位置误差的理想值Br进行对比。若在该αmax值限定条件下所有的Bavg均满足，则输出αmax值。若不满足条件，改变αmax，再一次进入求解程序。

求解结果如图7所示，在满足测量精度要求的情况下，传感器数量n(以下简称n)与倾角范围αmax之间的关系。当所有比例系数α小于αmax时，测量误差都能满足要求。

图7 求解结果

整体来看，n的增加，αmax增大，测量误差的增幅呈现由小变大再变小的趋势。具体来说，当偏移范围过小时，容易造成如图4(b)的特殊情况，载流导体在空间内的移动范围将受到限制，因此导致n的增加对αmax的增幅较小。随着n的增加，当增加到一定量后，增幅减弱。特别是在δ≤±0.2%的情况下，当n>7时，αmax的增幅骤减至0。具体来看，在满足δ≤±1%的情况下，n为3个时，αmax被限制在26°以内。n=10时，αmax被扩大至49°。在满足δ≤±0.2%的情况，n=3时，αmax被限制在17°以内。n=10时，αmax被扩大至37°。可见，在圆形阵列均值法中，传感器数量n的增加可以减少位置信息对测量误差的影响(敏感性)。

4.2 硬件设计

图8为硬件电路图，主要包括多个TMR磁传感器、一个加法器和一个滤波器。在电路中利用加法器将传感器的输出电压进行叠加求和，并在后端电路中增加一个RC滤波器，以降低噪声的干扰。在实际设计中，R1,R2阻值为1 kΩ，R3阻值为20 Ω，C电容值为470 nf。

图8 硬件电路图

本文根据上述仿真结果，选择了满足δ≤±1%情况下的曲线进行研究，选择了传感器数量n=7的情况进行实物制作(在这个区间段内，随着传感器数量的逐渐增加，倾角范围依旧有增大的趋势)。传感器型号为多维科技的TMR2104，灵敏度为3.1mV/V/Oe，供电电压为5 V。

5 实验与讨论

本文搭建了一个测量系统(如图9所示)，导体的直径2.0 cm，额定电流为500 A。

图9 测量系统

设计的传感器阵列电子式电流互感器(ECT)放置在位置调节器的顶部，Fluke i1000s被用作参考CT。参考CT和设计的ECT测量的所有电流均由NI DAQ采集卡组成的测量系统进行监视，以估算测量精度。基于上述系统开展了一系列实验，包括：①没有位置偏差；②有位置偏差：导体移位；③有位置偏差：导体偏斜；④有位置偏差：导体移位和导体倾斜，所得测量结果列于表1～表3。可以看出，根据IEC标准60044-8[11]，设计的ECT可以满足测量CT的0.2级准确级。对比导体偏移和导体倾斜对测量误差的影响，可以看出导体倾斜引起的误差比导体偏移引起的误差大。如果同时存在导体倾斜和导体偏移，则误差是最严重的，但也可以满足1.0级准确级。

表1 设计ECT的测量误差(无倾角情况)

表2 设计ECT的测量误差(无偏移情况)

表3 设计ECT的测量误差(含倾角、偏移情况)

6 结论

本文针对载流导体在圆形阵列中的位置信息对测量误差的影响进行了详细分析，验证了在圆形阵列的均值法中结合限制载流导体的位置偏差范围可以起到良好的效果，使其具有较高的测量精度。为了满足不同的精度等级要求，分析并给出了ECT与被测导体之间的尺寸关系。该数据可以作为功率测量应用的参考。最后，设计并实现了一个新的ECT(7个单轴TMR传感器组成的圆形阵列)，设计的ECT在各种位置偏差中均可以达到1.0的准确级。