从一道高考题谈试题命制
山东 孙 浩
圆锥曲线问题是历年高考的主力军,也是高三复习备考的重头戏.但是在高三复习备考中却体现为用时多、收效低的特点,学生在历次考试中都作答不理想,试题得分率极低.下面笔者基于多年参与统考试题命制工作,从试题命制的角度谈谈看法,期望能给读者以启迪.
1.高考试题为命制试题提供优秀蓝本
命制试题经常会参考往年全国卷及各省市的高考试题,高考试题出题严谨,无论是考查的知识点、考查能力,还是命题角度都能给命制试题提供好的思路和想法,因此在命制试题时经常以高考试题为蓝本进行改编命制.

(1)求椭圆E的方程;
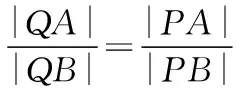
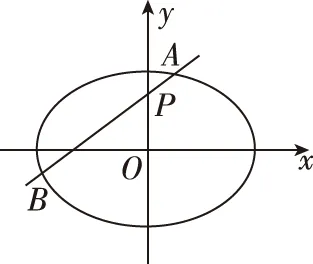
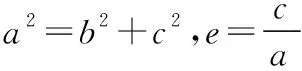
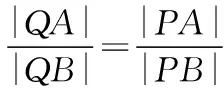
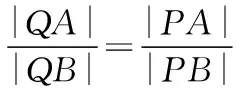
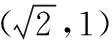

(2)当直线l与x轴平行时,设直线l与椭圆相交于C,D两点.

∴Q点在y轴上,可设Q点的坐标为(0,y0).
当直线l与x轴垂直时,设直线l与椭圆相交于M,N两点,
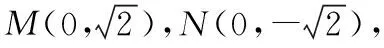

∴若存在不同于点P的定点Q满足条件,则Q点的坐标只可能为Q(0,2).
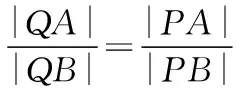
当直线l的斜率不存在时,由上可知,结论成立.
当直线l的斜率存在时,可设直线l的方程为y=kx+1,A,B的坐标分别为(x1,y1),(x2,y2).
其判别式Δ=16k2+8(2k2+1)>0,
∴kQA=-kQB,
∴∠PQA=∠PQB.
过点A,B向y轴分别作垂线AM,BN,垂足分别为M,N,则Rt△QMA∽Rt△QNB,
又Rt△PMA∽ Rt△PNB,
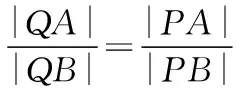

从这道高考试题的分析和解答过程可以看出,本题设置了求椭圆方程和两直线的斜率关系两个落脚点,试题命制围绕这两个落脚点而展开.下面谈谈依据这两个落脚点如何进行试题命制的.
2.以求椭圆的标准方程为落脚点进行试题命制
椭圆的标准方程含有a,b两个量,这两个量与c,e有直接关系,因此在试题命制中,一般是围绕a,b,c,e四个量来建构两个方程,思考这几个量与哪些知识点有关联,如何建立联系,围绕其中一个或几个量进行问题设计、建构关系式,从而达到考查有关知识和能力的目的.
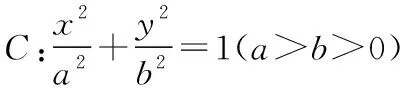

(1)求椭圆C的方程;
(2)略.
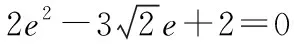
【详解】(1)由题意可得,
∴a=2.
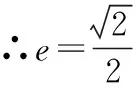
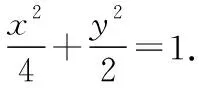
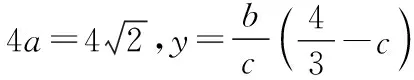
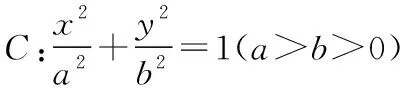
(1)求椭圆C的方程;(2)略.
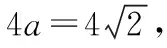
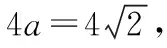

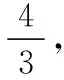
解得c=1或c=2(舍去),
∴b2=1,

通过上面两道试题的命制,发现以求椭圆的标准方程为落脚点的试题命制,先确立要求的椭圆标准方程是什么,然后根据a,b,c,e的具体值,从这些值中选取两个,围绕这两个值结合其他相关知识来设计问题,完成试题的命制.
3.以斜率为落脚点来命制考查直线与圆锥曲线位置关系试题
试题命制就是寻找一个问题有什么不同的说法,把这个问题延伸拓展一下,向前走几步或者向后退一退,寻找合适的说法进行化归与转化,把旧问题转化为新问题、新情境,实现新瓶装老酒,灵活考查知识、能力和数学核心素养.
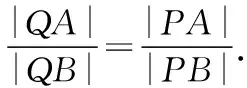
3.1 直接以斜率之间的关系来命制试题
命制试题时,考虑学生对知识掌握的程度,有时需要降低试题难度,直接给出斜率之间的关系,来考查学生的知识熟练度.
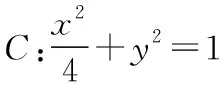
(1)略;
(2)在x轴上是否存在定点,使得直线TA与TB的斜率互为相反数?
【分析】(2)由题意可知,直线l的斜率存在且不为0,先假设存在定点并设为T(x0,0),用坐标直接表示出kTA,kTB,然后借助韦达定理就能求出满足条件的x0.
【题目1(2)改编题1】(2)在y轴上是否存在与点P不同的定点Q,使得直线QA与QB的斜率互为相反数?若存在,求出点Q的坐标;若不存在,请说明理由.
题目1经过这样改编,就成为一道直接考查两直线斜率关系的基础题.这种追根逐源,透过现象看本质的命题办法,在命制试题时经常使用.
3.2 以角度关系为切入点来命制试题
直线的倾斜角与斜率有着密切的联系,斜率问题向前走一步可以转化为角的问题来呈现,进而考查学生的化归与转化能力.
3.2.1直接给出角度关系
【题目1(2)改编题2】(2)在轴上是否存在与点P不同的定点Q,使得∠PQA=∠PQB?若存在,求出点Q的坐标;若不存在,请说明理由.
3.2.2 用线段比值设置问题,暗含角度关系
如果两个三角形相似,则对应角相等,对应线段成比例.因此,在命制试题时,可以以线段成比例为视角,通过恰当的化归与转化把问题转化为对应角相等,在问题中经常以构建直角三角形实现转化与沟通.
题目1第(2)问就是用线段比值的视角来命制的斜率问题.
3.2.3 借助面积比转化为角度问题

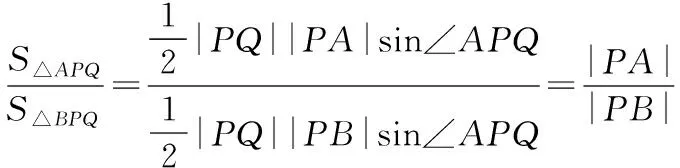
3.3 以直线过定点为切入点来命制试题
直线过定点可以转化为定点与两个动点连线的斜率相等,因此在命制试题时,可以用直线过定点来变相考查斜率问题.
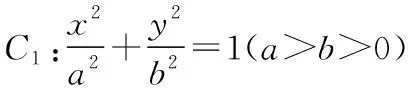
(1)略;
(2)过点A(-4,0)的直线l与椭圆C1交于M,N两点,点M关于x轴的对称点为E.当直线l绕点A旋转时,直线EN是否经过一定点?请判断并证明你的结论.
【分析】(2)当直线l的斜率为0时,直线l与椭圆C1交于M,N两点,则M,N两点为椭圆C1的左、右顶点,因此点M关于x轴的对称点E是点M本身,所以直线EN与x轴重合,由此可得直线EN若经过一定点,定点一定在x轴上,可设为T(x0,0).由题意可知,kTM=-kTE,然后根据kTE=kTN,结合韦达定理求出x0的值.
4.结束语
以考查椭圆的标准方程为落脚点命制试题时,围绕a,b,c,e四个关键基本量如何建构两个方程上下功夫,通过建构不同的方程来考查学生对基本知识和基本方法的掌握程度,不断变换考查角度,灵活设置问题,考查学生的数学核心素养.命制此类试题可以从以下几个方面思考如何设置问题,建立方程式:
①从考查椭圆定义的角度来命制试题;
②从考查椭圆性质的角度来命制试题;
③从考查点与椭圆的位置关系的角度来命制试题;
④从考查直线与椭圆的位置关系的角度来命制试题;
⑤从与其他曲线相结合的角度来命制试题.
以斜率为落脚点来命制考查直线与圆锥曲线位置关系命制试题时,可以直接考、间接考、变换考,把斜率、倾斜角、线段成比例和三角形面积等知识有机结合,不断变化命题角度,灵活设置问题考查学生知识的迁移度和数学核心素养.


