基于ADAMS根基土样破碎器的设计与仿真研究
李亚丽 湛小梅 崔晋波 曹中华


摘 要 针对目前在农业土壤研究中土壤超细粉碎技术难、相应机械缺乏等问题,本研究设计了一种根基土样破碎机,通过四杆运动机构驱动粉碎罐进行往复运动,其核心装置破碎罐半径为60 mm,碎土研磨球直径为25 mm,且通过弹簧卡位安装在摇杆上。借助MATLAB自带的fsolve函数得到了破碎罐的实时线速度方程,并基于ADAMS对该四杆机构进行仿真分析,得到该机构呈现垂直方向呈现抛物线式往复运动,运动周期为0.5 s,振幅为60 mm,运动轨迹较为理想,可为物理样机的研制提供参考。
关键词 根基土样;破碎器;ADAMS;设计;三维建模;仿真分析
中图分类号:S-3 文献标志码:A DOI:10.19415/j.cnki.1673-890x.2021.28.016
植物根基土样的研究需要土壤颗粒直径在0.1~10 μm的超细粉体,将土壤破碎为所需的超细粉体及相应的破碎技术可称超细破碎[1]。随着工业的快速发展,超细破碎作为一门新技术也在迅速发展。超细破碎大多用在药物的使用,药物可通过超细破碎机械使其超细化,使物质的界面性能和表面性能同时发生变化,但物质的化学成分不会被改变,从而达到一般物质粉体所无法达到的超常使用效果[2]。
目前在生态技术领域所采集的植物根部土样或者是各种试样等都是采集完送到实验室进行各种分析和技术处理以获取相应的实验数据,这其中许多的试样需要进行粉碎处理,许多实验室所采用的破碎机械都是利用垂片式刀具或者是旋转的锤子敲击的粉碎方法,采用这种方式进行粉碎的机具结构比较复杂,维修起来比较困难,而且对整机的密封条件要求极高,因此这种结构的破碎机械价格普遍较高,并且这种破碎机械对刀具的材料要求极高,这些问题给实验带来了许多的不便,造成不必要的经济损失。国内外制备超细粉体的机械粉碎设备主要有高速机械冲击式磨机、气流磨、介质搅拌磨、振动磨等[3-8]。其中,高速机械冲击式磨机和气流磨属于干法超细粉碎设备,而介质搅拌磨和振动磨既可用于干法超细粉碎也可作为湿法超细粉碎[9]。陈宇红进行的黄芪超细粉碎试验,使用功率为1.5 kW、频率为90 Hz的REGAKU高频振动磨,主要是通过正向压力和剪切力的联合作用对黄芪进行破碎[10],由于初期破碎时的速度较快,物质的分布范围会收缩,破碎后期分布范围会加大,且高频振动磨的成本较高。李成华和曹成奎进行的黑木耳超微粉碎试验,采用额定功率为1.5 kW的ZM-2型振动磨,主要是将物料和磨介质装于由弹簧支承的粉碎筒体内,电机通过挠性联轴器驱动偏心激振器产生扰动力,驱动粉碎筒体高频振动,使筒体内的物料和磨介质产生抛射、冲击、剪切、摩擦和旋转运动而被粉碎[11]。由于以上的超细破碎机械,破碎物质的过程中机械会受到强烈的冲击、碰撞、摩擦等作用,不仅降低了设备的使用寿命,又对产品造成了污染,且大多数破碎机械被广泛应用于高档涂料、医药、高技术陶瓷、微电子及信息材料、高级耐火及保温材料、填料和新材料产业等[12],价格较高,目前暂缺适宜用于小型科研如土壤研究等的价格不高的超细破碎机械。
本文设计一种根基土样破碎器,以解决目前生态技术领域对土壤分析时土壤粒度问题。采用CATIA软件对根基土样破碎机进行三维建模,并借助ADAMS软件对所建模型进行仿真分析,提高根基土样破碎器的铰链四杆机构可靠性,合理匹配破碎器,达到根基土样破碎的标准。
1 结构组成及工作原理
1.1 设计思路
1)偏心板和摇臂的长度均不能太大,尽量减小根基土壤破碎器的整体结构尺寸;
2)要保证破碎器在破碎根基土壤时偏心板不能反转,以免破坏电动机;
3)要保证碎土罐中的钢珠高速往复运动将根基土壤超细破碎;
4)要保证偏心板转动灵活;
5)偏心板和摇臂要有足够的强度和硬度;
6)要保证其结构简单,方便维修维护;
7)要适用于各种物料,粉碎比大,能干法生产也能湿法生产;
8)要保证有很好的密封性,可防止粉尘飞扬;
9)尽量减小整体的能量消耗。
1.2 结构组成
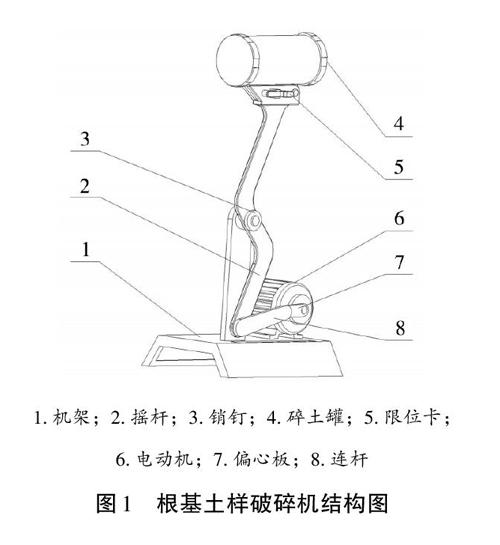
如图1所示,根基土壤破碎器主要由机架、电动机、偏心板、连接板、摇杆和碎土罐等部件组成,其中碎土罐由密封盖、托网和碎土研磨球等部件组成,且密封盖与碎土罐之间采用螺纹连接。机架与摇杆通过摇杆中部的孔连接由挡圈限定其位置,摇杆的一端与碎土罐通过销钉连接,碎土罐可以活动其通过限位卡与摇杆固定,摇杆的另一端与连接板的一端相连,连接板的另一端与偏心板的一端连接,偏心板的另一端与电动机连接,电动机通过螺栓连接于机架后部。
1.3 工作原理
生态要素采集器采集的根基土样放入碎土罐中,当电动机通电运转的时候,偏心板作旋转运动,偏心板带动连接板作往复式运动,连接板带动摇杆作往复式摆动,由于碎土罐与摇杆连接,因此碎土罐往复运动,钢球在碎土罐里高速往复运动,在碎土罐内与土块碰撞以达到粉碎的作用。碎土罐的一個连接孔与摇杆通过销钉连接,另一个连接孔由限位卡固定。当要粉碎土块时,首先按下限位卡,将碎土罐转到竖直方向,然后加入土块,盖紧密封盖,将其恢复到原始的位置,放开限位卡,在弹簧的作用下使限位卡回到原来的位置固定碎土罐,粉碎完采取同样的方式,只是在此时打开下方的密封盖,由于有托网,钢珠不会落出。
2 关键零部件的设计
2.1 碎土罐设计
碎土罐是根基土样破碎器的关键部件,其主要作用是将生态要素采集器采集的根基土样放入碎土罐中,作往复运动可将土块超细破碎。如图2所示,碎土罐主要由密封盖、托网和碎土研磨球等组成,碎土罐的两端设置密封盖,密封盖上设有托网,密封盖与碎土罐体之间采用螺纹连接,其内部设有碎土研磨球,碎土罐可以活动其通过限位卡与摇杆固定。
碎土罐的罐体材料为45钢,其半径为60 mm。为了保证土块在碎土罐中能够快速有效地被粉碎,碎土罐中放有大小相等的碎土研磨鋼球,钢球的直径为25 mm。钢球的直径太小与土块的接触面积小,不利于土块的超细粉碎;钢球的直径太大,钢球之间及钢球与罐体之间的碰撞面积增大,碎土罐的损伤就增加。密封盖上托网的作用是漏掉被粉碎的土壤,使钢珠不会下落及对其往复运动时有弹力,可以加快钢球往复运动的速度,使钢球与土块高速碰撞,可加快土块的粉碎。
2.2 摇杆设计
如图3所示,摇杆为“S”形,其头部为“ㄈ”形,设有与碎土罐连接的孔,在头部设有限位卡和复位弹簧。
3 建立数学模型对破土器进行分析
所研制的根基土样破碎器是一个四杆机构,采用矿山机械中利用钢球粉碎的原理,将其运用到小型粉碎机械上来从而研制出的一种新的小型粉碎机械。如图4所示为根基土样破碎器的运动分析简图,在图中OA杆为偏心板,作为主动件且角速度为ω,AB杆是连杆,一端与偏心板铰接,另一端与摇杆BC中间部分铰接,对于破土罐安装在摇杆BC的端部,分析破土罐作往复运动时的最大速度,在最大速度时破土钢珠的运动最快,且对土块的破碎效果最好。
依据图4进行设定,四杆机构中各杆的长度分别为l1=72 mm,l2=160 mm,l3=260 mm,l=320 mm,l4=300 mm,偏心板以角速度ω=180 rad·s-1作匀速转动。可将铰链四杆机构看作为一个封闭多量多边形[13-16],分别以l1、l2、l3、l4表示各构件的矢量,θ1、θ2、θ3表示图4中的三个角,该机构的封闭矢量方程式以复数形式表示为:[l1eiθ1+l2eiθ2=l4+l3eiθ3] (1)
规定角θ应以x轴的正向逆时针方向度量,按照欧拉公式[eiθ=cosθ+isinθ]展开可得
[l1(cosθ1+isinθ1)+l2(cosθ2+isinθ2)=l4+l3(cosθ3+isinθ3)] (2)
方程式(2)的实部和虚部应分别相等,即
[l1cosθ1+l2cosθ2=l4+l3cosθ3l1sinθ1+l2sinθ2=l3sinθ3] (3)
消去θ2后可得
[acosθ3+bsinθ3+c=0] (4)
方程式(4)中的系数分别为[a=l4-l1cosθ1],[b=-l1sinθ1],[c=a2+b2+l23-l222l3],又因[sinθ3=2tan(θ3/2)1+tan2(θ3/2)],[cosθ3=1-tan2(θ3/2)1+tan2(θ3/2)],分别将其代入方程(4)中可得关于tan(θ3/2)的一元二次方程式,由此可解出摇杆BC的角位移θ3,即
[θ3=2arctanb±a2+b2-c2a-c] (5)
(5)式中θ3有两个值,说明摇杆BC在作往复运动时会与x轴有两个不同的夹角,是根据摇杆BC的初始位置和连续运动条件来决定的[17]。
将式(1)对时间求导可得
[l1ω ieiθ1+l2ω2ieiθ2=l3ω3ieiθ3] (6)
为了消除θ2,将式(6)的两边同时乘以[e-iθ2]可得
[l1ω iei(θ1-θ2)+l2ω2iei(θ2-θ2)=l3ω3iei(θ3-θ2)] (7)
按照欧拉公式展开后,取实部可得摇杆BC的角速度ω3,即
[ω3=ω l1sin(θ1+θ2)l3sin(θ3-θ2)] (8)
将式(6)对时间再求导数可得
[-l1ω2eiθ1+l2α2ieiθ2-l2ω22eiθ2=l3α3ieiθ3-l3ω23eiθ3] (9)
为了消除α2,将式(9)两边同时乘以[e-iθ2]可得
[-l1ω2ei(θ1-θ2)+l2α2i-l2ω22=l3α3ieiθ3-l3ω23eiθ3] (10)
对上式中两边分别取实部可得摇杆BC的角加速度α3,即
[α3=l2ω22+l1ω2cos(θ1-θ2)-l3ω23cos(θ3-θ2)l3sin(θ3-θ2)] (11)
角加速度的正、负号可表明角速度的变化趋势,角加速度与角速度同号时表示加速,反之则为减速[18]。
应用数学方式对以上各式进行求解,方法如下:
[dsinθdt=dθdtcosθ=ωcosθdcosθdt=dθdtsinθ=ωsinθ(uv)'=u'v+v'u] (12)
由角位移方程式组(3)可求得非线性方程组,即
[ f1(θ3,θ4)=l1cosθ1+l2cosθ2-l4-l3cosθ3f2(θ3,θ4)=l1sinθ1+l2sinθ2-l3sinθ3] (13)
借助MATLAB自带的fsolve函数分别绘出BC摇杆的角速度ω3、角加速度α3与时间t的关系图。
则有BC端点F点处碎土罐的位移方程
[xF=l1cosθ1+l2cosθ2+(l3+l)cosθ3xF=l1sinθ1+l2sinθ2+(l3+l)sinθ3] (14)
将方程(13)对时间求一阶导数,得BC端点F点的速度方程,即
[xF·=-l1ωsinθ1-l2ω2sinθ2-(l3+l)ω3sinθ3yF·=l1ωcosθ1+l2ω2cosθ2+(l3+l)ω3cosθ3] (15)
则F点碎土罐的线速度为
[vF=xF·2+yF·2=l12ω2+l22ω22+(l3+l)2ω23+2l1ωl2ω2cos(θ1-θ2)+2(l3+l)ω3l1ωcos(θ1-θ3)+l2ω2cos(θ2-θ3)] (16)
4 ADAMS仿真分析
为了提高根基土样破碎器的铰链四杆机构在ADAMS中仿真分析[19-20]的可靠性,建模时应该遵循的原则如下。
1)采用从简单到复杂机构分析的渐进模式方法。在仿真建模的初始阶段,要保证铰链四杆机构中各铰点位置、质心位置及各部件质量的正确性。
2)对复杂机构进行仿真分析时,应将整个系统分解为若干个子系统,首先对各子系统进行仿真分析,最后进行整体系统的仿真分析。
3)ADAMS软件对虚拟样机仿真分析[21-22]应该尽量降低其规模,只考虑影响根基土样破碎器性能的构件。
在ADAMS环境中建立根基土样破碎器四杆机构ADAMS模型,其主动曲柄长度为72 mm,角速度为180 rad·s-1,主动曲柄长与水平地面的初始夹角为83.72°;连杆长度160 mm,机架杆长300 mm,摇杆BC长度260 mm,CF长度320 mm。整个机构有四个转动副和1个马达,分别在主动曲柄与机架之间建立转动副,在主动曲柄与连杆之间建立转动副,在连杆与摇杆之间建立转动副及摇杆与机架之间建立转动副,在主动曲柄与机架之间的转动副上建立马达[23]。
根基土样破碎器通过与破碎罐接触的摇杆末端来反应该四杆机构的运动特性,其随时间摇杆末端的垂直方向位移变化曲线如图5所示。可知四杆机构破碎运动曲线先下滑,在0.18 s处达到极值,随后开始上扬,整体呈现往复式运动规律[24],完成一个周期时间为0.50 s。其整体在垂直方向的位移量变化较为平缓,最大高度差为60 mm,避免了碎土研磨球将土壤夯实在托网上,难以分筛。
5 结论
1)根据对碎土标准和便于维护等方面的考虑,本文设计了根基土样破碎器,并重点对碎土罐、摇杆等关键零部件进行了分析,认为能够解决根基土壤超细粉碎的要求,可为破碎机的研发提供依据。
2)根据根基土样破碎机四杆机构的设计,借助MATLAB自带的fsolve函数分别绘出摇杆的角速度、角加速度与时间的关系,也确定了其线速度方程,得到最大线速度。
3)仿真结果证明,该破碎罐垂直方向进行抛物线式往复运动,一个运动周期为0.5 s,最大运动高度差为60 mm,趋势较为平缓,可有效降低土壤夯实过紧的问题。基于ADAMS参数化分析法对复杂运动机构的优化设计更加高效和便捷,为物理样机的研制提供了参考。
参考文献:
[1] 李凤生主编.超细粉体技术[M].北京:国防工业出版社,2003.
[2] 郭天德.振动磨的发展及降低能耗途径[J].中国非金属矿工业导刊,1999(5):79.
[3] 郑水林.超细粉碎原理、工艺设备及应用[M].北京:中国建材工业出版社,1993.
[4] 张少明.粉体工程[M].北京:中国建材工业出版社,1994.
[5] 杨伏生,周安宁,葛岭梅.我国超细粉碎技术现状与发展趋势[J].化工矿物与加工,2001(5):1-6.
[6] 盖国胜.超细粉碎与分级技术进展[J].中国粉体技术,1999,2(1):22-26.
[7] 张国旺.破碎粉磨设备的现状及发展[J].粉体技术,1998,9(3):37-42.
[8] 尹邦跃,王零森,边立刚,等.B4C粉末的滚动球磨、振动球磨和气流粉碎[J].粉末冶金技术,2001,19(6):361-364.
[9] 张更超,应富强.超细粉碎技术现状及发展趋势[J].2003(5):35-37.
[10] 陈宇红.高频振动磨超细粉碎黄芪试验研究[J].中国粉体技术,2008(1):33-35.
[11] 李成华,曹成奎.振动磨超微粉碎黑木耳的试验研究[J].农业工程学报,2008,24(4):246-250.
[12] 张更超,应富强.超细粉碎技术现狀及发展趋势[J].煤矿机械,2003(5):35-37.
[13] 赵勾.机构数值分析与综合[M].北京:机械工业出版社,2005.
[14] 刘天祥,杨丽,范武君,等.基于MTLAB插秧机分插机构运动轨迹分析[J].黑龙江八一农垦大学学报,2006,18(6):47-19.
[15] Guo L S,Zhang W J. Kinematic analysis of a rice transplanting mechanism with eccentric planetary gear trains[J]. Mechanism & Machine Theory, 2001, 36(11-12):1175-1188.
[16] 何岳平.自走式大蒜栽植机关键部件研究与设计[D].南京:南京农业大学,2009.
[17] 王知行,邓宗全主编.机械原理(第二版)[M].北京:高等教育出版社,2006.
[18] 郑文纬,吴克坚主编.机械原理(第二版)[M].北京:高等教育出版社,2012.
[19] 顾佳.基于虚拟软件的收割机割台建模和运动仿真研究[J].农机化研究,2021,43(3):128-132.
[20] 赵玲亚,王英健,赵子开.圆形水果采摘机械手运动学分析与仿真[J].中国农机化学报,2020,41(3):24-29.
[21] 张莉,郭巧惠,徐嘉.基于ADAMS的花生收获机清选装置设计与仿真研究[J].农机化研究,2017,39(3):53-57.
[22] 赵亮,薛忠,王凤花,等.基于ADAMS的木薯茎秆切割过程虚拟仿真研究[J].中国农机化学报,2018,39(4):21-24.
[23] 赵武云.ADAMS基础与应用实例教程[M].北京:清华大学出版社,2012.
[24] 杨亚洲,顾炳龙,刘宽厚,等.基于Adams的花生脱壳机转速的优化研究[J].中国农机化学报,2017,38(9):55-59.
(责任编辑:丁志祥)

