基于度中心性局部扩展的社区划分算法∗

柳曾雄 施化吉 李 雷 施磊磊 孙祥瑜

（江苏大学计算机科学与通信工程学院 镇江 212013）

1 引言

随着通信技术和互联网的高速发展，移动智能设备日渐普及，社交网络作为移动互联的核心应用，已成为人们日常沟通交流的重要渠道。根据新浪官方发布的2019年Q2财务报表显示，新浪微博第二季度营收4.318亿美元，六月活跃用户高达4.86亿。社交网络具有实时性强、数据庞大、覆盖用户广泛和关系维度复杂等特点，吸引了学术界大量学者的关注，成为热门的研究方向。

社交网络作为人类社会在虚拟网络中的延伸，在人们日常生活中扮演了愈加重要的角色，它弱化了空间的概念，使得世界上任何位置的两个人都可能在社交网络中相遇。因此社交网络也具备了社区属性，它是社交网络模块化［1］特性的一种体现。目前学术界没有对社交网络的社区属性作一个统一定义，如若把社交网络映射到图结构：用户实体对应节点，用户关系对应节点间链接，社区则是子图结构，社区内部节点链接相比于社区之间更为密集。社区结构在一定程度上反映了真实的社会关系，不同的社区往往代表了不同的用户群体，如亲友、同城交友、明星粉丝等群体，该群体内的用户往往具有相同兴趣或属性特征。社区划分的研究为网络演化、链接预测、影响力分析以及信息传播等方向提供了理论依据，在优化基础网络设施、好友推荐、商业营销，舆情监测等领域有着重要的实际应用价值。

社交网络规模的进一步扩大，对社区划分研究提出了更高的挑战。由于高昂的时间复杂度原因，一些经典的社区划分算法［1］已无法满足性能要求，而基于局部扩展思想的社区划分算法［2］从局部出发，逐步扩展，而非考虑整个网络信息，能快速发掘出社区结构，适用于大规模的网络中。然而，基于局部扩展思想的社区划分算法存在稳定性问题，随着选择初始种子和扩展方向的不同，算法运行可能得到截然不同的结果。

针对基于贪婪优化Surprise函数的社区划分算法［3］（AGSO）初始种子链接随机选择策略而导致不稳定性问题，本文以AGSO算法为基础进行改进，提出了一种基于度中心性局部扩展的社区划分算法（Community Detection Algorithm Based on De⁃gree-Centralized Local Extension，DCLE）。在初始链接选择阶段，计算每个节点的度中心性［4］（De⁃gree Centrality），其次将网络链接两端节点的度中心性之和作为链接的度中心性并降序排序，将度中心性最大的链接作为初始链接加入网络结构中。避免了AGSO算法随机选择而带来的不稳定性问题，提高算法性能和生成社区的质量。

2 相关工作

近些年，诸多学者在社区划分方向作出大量探索和研究工作，涌现了一大批优秀的科研成果，诸多社区划分算法已经应用到了实际。其中最为经典的是由Newman和Grivan［1］提出的基于分裂思想的GN算法。GN算法不断删除网络中具有最大边介数的链接，直至网络中所有的链接都被删除。GN算法的时间复杂度为O（m2n），其中m为网络中链接的数量，n为网络规模，因此GN算法不适用于大规模的网络结构，但其开创了社区划分领域的先河，具有重要意义。为了优化GN算法时间复杂度问题，Newman等［6］随后提出了基于聚类思想的CNM算法，首先将网络中每个节点初始为社区，其次按照模块度Q增量进行社区合并，直至整个网络结构的模块度Q值无法增大。但CNM算法存在分辨率问题［7］，在大社区和小社区的共存网络结构中性能不佳。Reghavan等［8］首次提出了LPA算法，通过向邻居节点传递标签，最终拥有相同标签的节点属于同一个社区。LPA算法拥有将近线性的时间复杂度，已被广泛应用。Gregory［9］提出了COPRA算法以识别重叠社区问题，允许一个节点携带多个标签和隶属度，并随机选择节点更新标签。刘世超等［10］提出了基于标签传播概率的重叠社区发现算法LPPB，通过网络结构信息计算标签传播的概率。冷作福［3］提出了一种基于贪婪优化Surprise函数的社区划分算法［3］（AGSO），该算法从局部扩展，将Surprise增量最大的边依次加入到网络中，每次扩展迭代过程中，该算法不考虑剩余全部候选链接，而是将已加入链接的邻近链接加入到网络中，直至候选链接集合为空或所有候选链接都使网络的Surprise值增加时，算法结束。该算法基于贪婪思想进一步降低了时间复杂度，且不存在分辨率问题，但算法选取初始链接时使用随机策略，不同的初始链接直接导致不同的精度和性能，多次执行将得到不同的结果，最终取最优值作为社区划分结果。

3 概念及定义

3.1 社交网络

社交网络作为真实社会在网络世界中的延伸，可以抽象为图结构G=（V，E），其中V=｛v1，v2，v3，…，vn｝为网络中节点集合，n=|V|表示网络节点的数量，E=｛eij|，vi，vj∈V，i≠j｝表示链接关系集合，其中表示节点vi和vj之间存在链接关系。

3.2 社区结构

社区是网络拓扑图中的子图结构，如图1所示，社区结构内部节点链接的密度高于社区之间链接的密度，意味着社区内部关系更为密切，也符合对现实社会社区的认知。

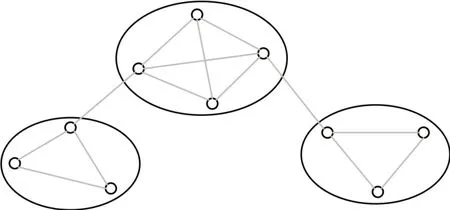
图1 社区结构

3.3 度中心性

在无向图中，度（Degree）表示该节点的邻边的个数。度越大表示该节点在网络中越重要，而大型网络中节点的度往往很大，无法直观地度量节点的重要程度，因此采用度中心性［4］（Degree Centrality）作为节点在网络中重要程度的直接度量。一个节点的度中心性越大，表示该节点在网络中邻边越多，影响力越大。度中心性是社交网络中影响力的一种度量方式，其测量和节点的度直接相关，计算公式为

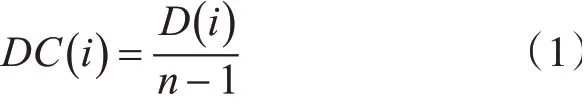
式中：D（i）为节点vi的度，n-1表示节点vi和其它所有节点最大可能产生的链接数。节点vi度中心性DC（i）取值在0～1之间，DC（i）=0表示节点vi和其他任何节点都没有链接，DC（i）=1表示节点vi和其他所有节点都有链接关系。

3.4 评价指标

3.4.1 模块度Q函数

模块度Q函数最早由Newman和Girvan提出，定义为网络结构中社区内部链接所占比例与随机网络中社区内部链接比例期望的差值。通常用模块度Q值衡量社区划分的质量，Q值越大，表明划分的社区结构准确性越高。模块度Q函数公式为

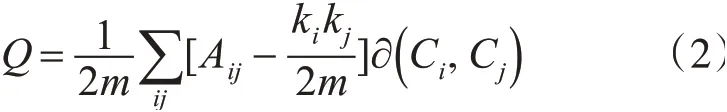
式中：m为网络中链接总数，Aij表示网络对应邻接矩阵的一个元素，当vi和vj之间存在链接关系时，Aij为1，否则为0；ki表示节点的度；∂（Ci，Cj）表示社区Ci和Cj是否相同，Ci=Cj时为1，否则为0。

3.4.2 Surprise函数

Surprise函数［7］是一种区别于传统Q函数的模块化评价指标，它描述了在给定该随机模型的情况下，网络的某个划分与社区节点和链接的期望分布之前的距离。其公式为

式中：F表示网络结构中最大的链接数；n表示网络中实际的链接数；M表示网络中社区之间最大的链接数；p表示社区内部实际的链接数。实验表明，Surprise函数不存在分辨率问题。Surprise值越大表示社区划分的结果越接近真实的社区结构。

3.5 AGSO算法

AGSO算法［3］是一种基于Surprise函数的局部扩展社区划分算法，其根本出发点在于网络结构的模块度特性，即社区内部的链接紧密，而社区之间的链接较为稀疏。如若l是社区内部的一条链接，那么l周围链接也很有可能是社区内部的链接。因此将链接l加入到网络中后，不必考虑剩下全部的候选链接，仅仅考虑链接l附近的候选链接，这样能减少搜索空间，极大程度上降低时间复杂度，提升社区划分的效率。但是AGSO算法存在分辨率问题，原因在于AGSO算法第一步，无论将哪条链接加入到网络中，Surprise增量都是相同的，因此文献作者在初始链接选择阶段，随机选择一条链接加入到网络中，多次实验后取最优值作为最终结果。

4 DCLE算法

4.1 算法思想

DCLE算法是一种基于度中心性局部扩展的社区划分算法，针对AGSO算法初始链接选择随机而导致的稳定性问题，DCLE算法在初始种子链接选择阶段，引入节点和链接的度中心性概念，根据社区结构内部链接较为密切这一特性，节点度中心性越高，则节点处于社区内部的概率越大，在扩展阶段，每次将链接加入网络结构中后，不再考虑剩下所有的链接，仅仅将该已加入网络中的链接的邻近链接作为候选链接。依次计算所有候选链接加入网络后的Surprise增量，将Surprise值增量最大链接加入到网络中，并将该链接从候选集合中删除，直至所有链接都无法使网络Surprise值增加或候选链接集合为空时，算法结束，得到社区划分结果。

算法步骤如下。

输入：节点集合V，链接集合E，已加入网络链接集合added_edges，其邻近节点集合added_nei⁃bor_vertices，以及邻近链接集合added_neibor_edges

输出：社区集合C

1）初始化网络为n个节点和0条链接；

2）根据式（1）计算所有节点v的度中心性；

3）将链接e两端节点的度中心性之和作为链接的度中心性，并降序排序；

4）将度中性最高的链接作为种子链接，加入到网络中，计算当前Surprise增量，并依次更新added_edges，added_neibor_vertices和added_neibor_edges集合，执行步骤5），直至added_neibor_edges集合为空；

5）依次计算added_neibor_edges中链接加入到网络中的Surprise增量，将增量最大的链接从add⁃ed_neibor_edges中移除并加入到added_edges，依次更新added_neibor_vertices和added_neibor_edges，并保存当前网络的Surprise值。循环执行步骤5），直至所有链接都无法使网络的Surprise值增大或added_neibor_edges集合为空。

4.2 算法复杂度分析

给定节点数为n和链接数为m的网络，DCLE算法时间复杂度如下。

1）计算所有节点度中心性需要时间复杂度为O（n）；

2）计算所有链接度中心性需要时间复杂度为O（m）；

3）迭代过程中，链接扩展需要时间复杂度为kclink2d，其中k为社区数量，clink为社区内部加入链接的平均个数，d是网络节点平均度。

综合上述分析，DCLE算法的时间复杂度为m+n+kclink2d，略高于AGSO算法，但由于AGSO算法不稳定性问题而采用多次运行取Surprise最优值策略，DCLE算法最终运行时间低于AGSO算法。

5 实验结果与分析

DCLE算法在理论上有较好性能，解决了AG⁃SO算法不稳定性问题，为了验证算法在真实网络上的可行性，本节分别在Zachary Karate Club网络和多个LFR人工生成网络上对DCLE算法进行实验，并将其与AGSO算法在相同实验条件下对比分析。其中AGSO算法对初始种子选择敏感，因此分别运行十次取最优值作为最终运行结果，并将模块度Q函数值和Surprise值作为评价指标。

5.1 Zachary Karate Club数据集

Zachary Karate Club网络［11］为社会学家Zachary历时两年观察美国某一空手道俱乐部34名成员之间社会关系得到的关系网络，包含34个节点和78条链接，其网络结构如图2所示，该数据集是社区发现领域中的经典数据集。

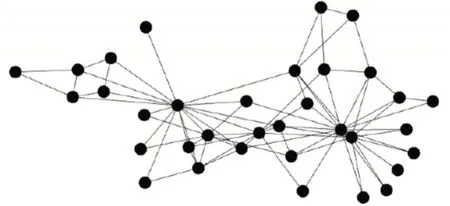
图2 Zachary Karate Club网络结构

表1 Zachary Karate Club数据集

DCLE算法和AGSO算法在Zachary Karate Club数据集上的实验结果如表2所示。由于AGSO算法初始链接选择随机，因此运行十次，得到十组模块度Q值和Surprise值。从表2可以看出，AGSO算法在Zachary Karate Club网络上运行得到模块度Q值和Surprise值处上下波动状态。

表2 Zachary Karate Club数据集实验结果

其中第四次结果最为理想，同DCLE算法实验结果一致，即AGSO算法初始链接选择为度中心性最大链接时，可以得到最优模块度Q和Surprise值；当初始链接选择为社区内部链接时，AGSO算法也能得到较好的结果；而当初始链接选择为社区之间链接时，AGSO算法得到的模块度Q和Surprise值较低。DCLE算法和AGSO算法的模块度Q值和Sur⁃prise值曲线分别如图3和图4所示。

图3 模块度Q值曲线

图4 Surprise值曲线

在小概率（同链接规模成反比）情况下，DCLE算法结果和AGSO算法一致；其他情况下DCLE算法的社区质量要优于AGSO算法，能稳定且准确地发觉社区结构。

5.2 LFR人工网络数据集

LFR网络［14］是同真实数据集极为相似的人工生成数据集，可以通过配置参数以模拟各类场景，配置参数包括节点个数N、混杂参数μ、节点平均度k、节点最大度kmax、最小社区规模cmin和最大社区规模cmax。为了验证DCLE算法在大型网络结构中的性能，本文生成如表3所示的多个人工网络结构。

表3 LFR网络数据结构

图5展示了DCLE算法和AGSO算法在不同规模LFR网络上的实验结果对比情况。左侧为DCLE算法运行得到的Surprise值，而右侧为AGSO算法多次运行后取Surprise最大值。在初始种子链接选择阶段，相比于AGSO算法的随机选择，DCLE算法初始选择社区内部链接，直接导致DCLE算法运行最终得到的Surprise值要高于AGSO算法。表明在大型网络结构上，DCLE算法的性能也要优于AGSO算法。

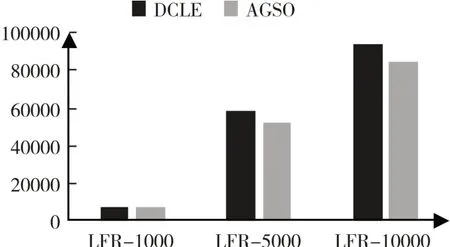
图5 LFR数据集实验结果

综上所述，DCLE算法拥有良好的运行性能，解决了AGSO算法的稳定性问题，可以快速而准确地发掘复杂网络中的社区结构，提升了所划分社区的质量。

6 结语

针对AGSO算法由于初始链接选择使用随机策略而导致的社区划分结果不稳定问题，本文提出一种基于度中心性的局部扩展DCLE算法以对其进行改进。通过计算网络节点的度中心性，并将链接两端节点的度中心性之和作为链接的度中心性并排序，将度中心性最高的链接作为初始链接并加入到网络中。在局部扩展过程中，仅考虑已加入链接邻近的链接作为候选链接，不再考虑剩下所有的链接，提高了社区划分的时间效率，保证了社区划分结果的稳定性。基于Zachary Karate Club和LFR人工生成网络数据集上的实验表明，相比于AGSO算法，DCLE算法的运行时间低，而稳定更高，验证了基于度中心性局部扩展的社区划分算法在社区划分方向的可行性和有效性。当然，本文仍然存在需要提高的部分，如每次加入链接后，都要计算一次Surprise增量，如何提出一种更高效的方式去衡量链接扩展的效果，有待进一步的研究。