部分主要构造对斜拉桥自振特性的影响分析

薛家伟 文坡 董世赋

摘 要：斜拉桥的动力特性分析是研究斜拉桥动力行为的基础，本文以全福河大桥为背景，使用ANSYS软件建立了空间有限元模型，详细分析了索塔单元划分、辅助墩、边界约束条件对斜拉桥自振特性的影响。

关键词：斜拉桥;自振特性;有限元法

中图分类号：U448 文献标识码：A

0 引言

斜拉桥的动力特性分析是研究斜拉桥动力行为的基础，其自振特性决定其动力反应特性，分析斜拉桥自振特性意义重大。结构的动力特性取决于结构的组成体系、刚度、质量和支承条件等。因此建立理想的大跨度斜拉桥动力分析模型，并进行自由振动分析，掌握其动力特性，具有十分重要的现实意义。

1 桥梁概况

全福河大桥跨径组合为156.5+324+156.5 m，上塔、中塔、下塔柱高分别为52.832 m、41.118 m、25 m。设计行车速度60 km/h;设计荷载为公路-Ⅰ级;设计洪水频率为1/300;通航等级为Ⅳ级。

2 有限元模型

大跨度斜拉桥的斜拉索在主梁上锚固点一般不会通过主梁扭转形心，当考虑斜拉桥同时受到多个方向的荷载时，一般需进行空间分析。本文将斜拉桥结构离散为杆、梁单元模型和索膜、梁单元模型两种模型。

3 斜拉桥部分主要构造对自振特性的影响分析

3.1 索塔单元划分对斜拉桥自振特性的影响

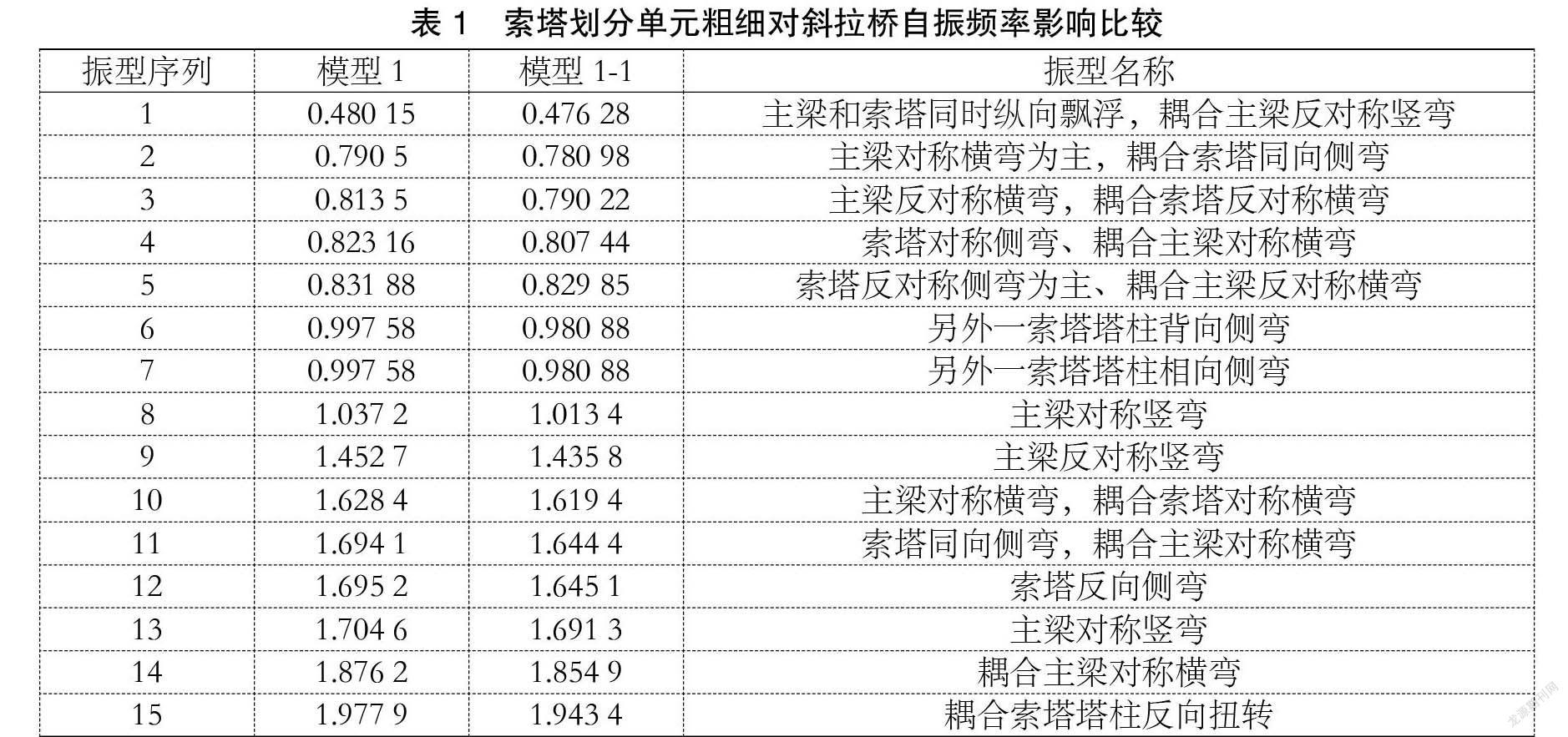
现对塔的模型划分粗细两种进行自振频率比较，第一种情况把单个主塔划分为87个单元，所用模型是基本模型1;第二种情况把每个索塔划分64个单元，采用的模型称为模型1-1。两种情况的振型和频率见表1。

从上表比较可见，两者振型出现顺序相同，但模型1-1较基本模型1的各阶频率要稍小，表明基本模型结构堆聚质量分配和节点位移更合理，计算结果更精确。也可从各阶频率数值可见，两者在桥梁结构自由振动时影响差异不大，平时在动力特性计算时可以忽略这部分的影响。但有关文献提到，索塔单元划分得粗對塔中间单元弯矩的分布影响较大，因此建议对塔单元的划分不宜太粗。

3.2 辅助墩对斜拉桥自振特性的影响

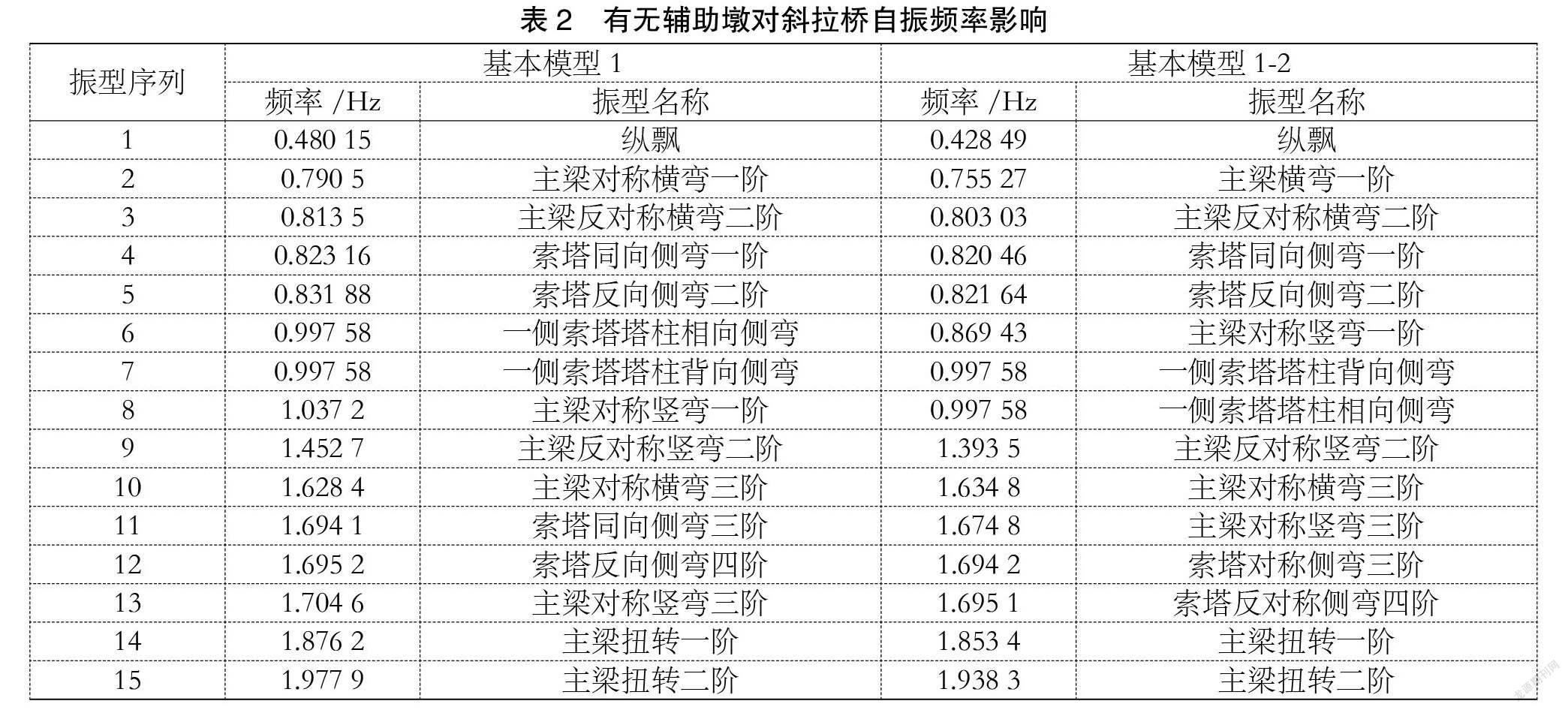
全福河大桥在边跨接近交界墩处各设计了一座辅助墩，现分析辅助墩的有无对桥梁自振特性的影响。在无辅助墩情况下的模型称为模型1-2，其与基本模型1的振型和频率比较见表2。

从表中可见，有无辅助墩对斜拉桥各振型的序列、对应振型的频率值均有影响。模型1-2各阶振型频率较基本模型1几乎都有所降低，这表明辅助墩对斜拉桥的自由振动影响较大。另外，模型1-2的竖向振幅比基本模型1大，竖向振动较基本模型提前两阶出现，可见辅助墩对斜拉桥竖向刚度提高具有显著影响。

3.3 边界约束条件对斜拉桥自振特性的影响

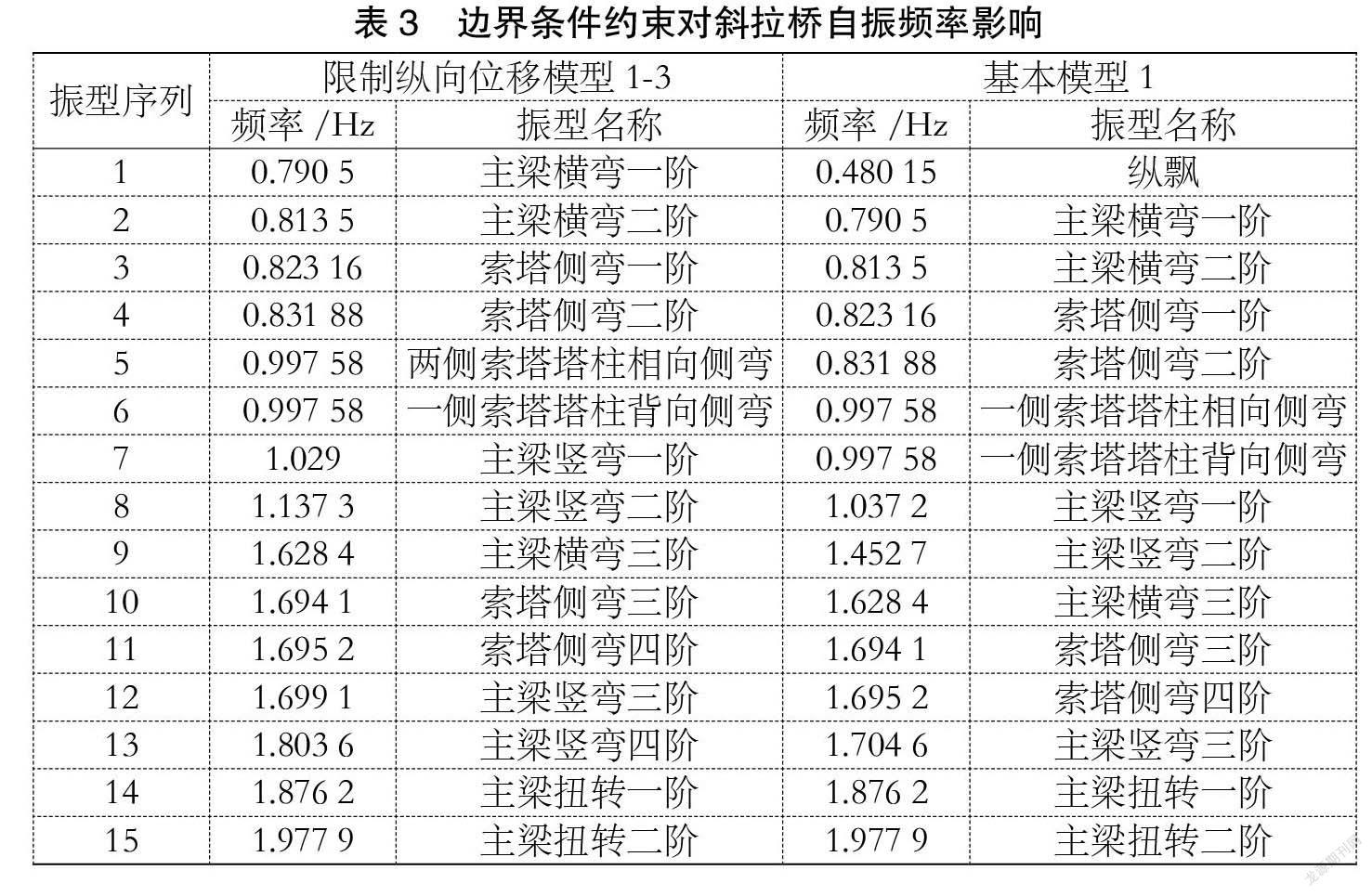
分两种情况分析约束条件对斜拉桥自振特性的影响：一种模型在主梁的一端设置一纵向约束，限制主桥的纵向位移，为模型1-3;另一种模型采用上述的基本模型1。两者计算所得的振型和频率比较见表3。

由上表可见，由于主桥纵向位移受到限制，斜拉桥第一阶振动为主梁对称横向弯曲，基频0.790 5 Hz，大于模型1的基频0.480 15。而对于基本模型1，由于纵向主桥位移约束解除，桥面的第一阶振动为纵向飘浮，斜拉桥结构的基频降低，地震反应随之减小。从上表还可以看出，两种情况下斜拉桥的横弯和竖弯、扭转基频几乎相同，可知，限制桥梁纵向位移对斜拉桥横向、竖向及扭转刚度影响不大，桥梁抗震性能得到一定改善。

4 结论

（1）索塔单元划分的粗细程度对斜拉桥自振频率影响不大，但对静载计算过程中索塔单元弯矩影响较大，建议不宜划分太粗。

（2）辅助墩对斜拉桥竖向自由振动影响明显，使斜拉桥竖向刚度明显提高。

（3）解除纵向约束的全飘浮体系斜拉桥，第一阶振动由横向对称弯曲变为纵向飘浮，该桥基频也由0.790 5变为0.480 15，桥梁抗震性能得到了较大改善。

参考文献：

[1]易日.使用ANSYS6.1进行结构力学分析[M].北京大学出版社，2002.

[2]姚令森.桥梁工程[M].人民交通出版社，1999.