积累数学活动经验，寻求知识建构衔接

麦满棠

【摘要】在《比例尺的应用》教学中，如何在教学中引导学生对前后知识进行有效的沟通与联系，帮助学生走出问题解答时“算法正确，就是难对”的怪象。本文将通过“沟通联系——巧设冲突——破构重建”三个层面，寻求知识建构的无缝衔接，帮助学生打通知识之间的隔断墙，追寻数学知识的本质。

【关键词】小学数学;知识建构;深化理解;积累经验

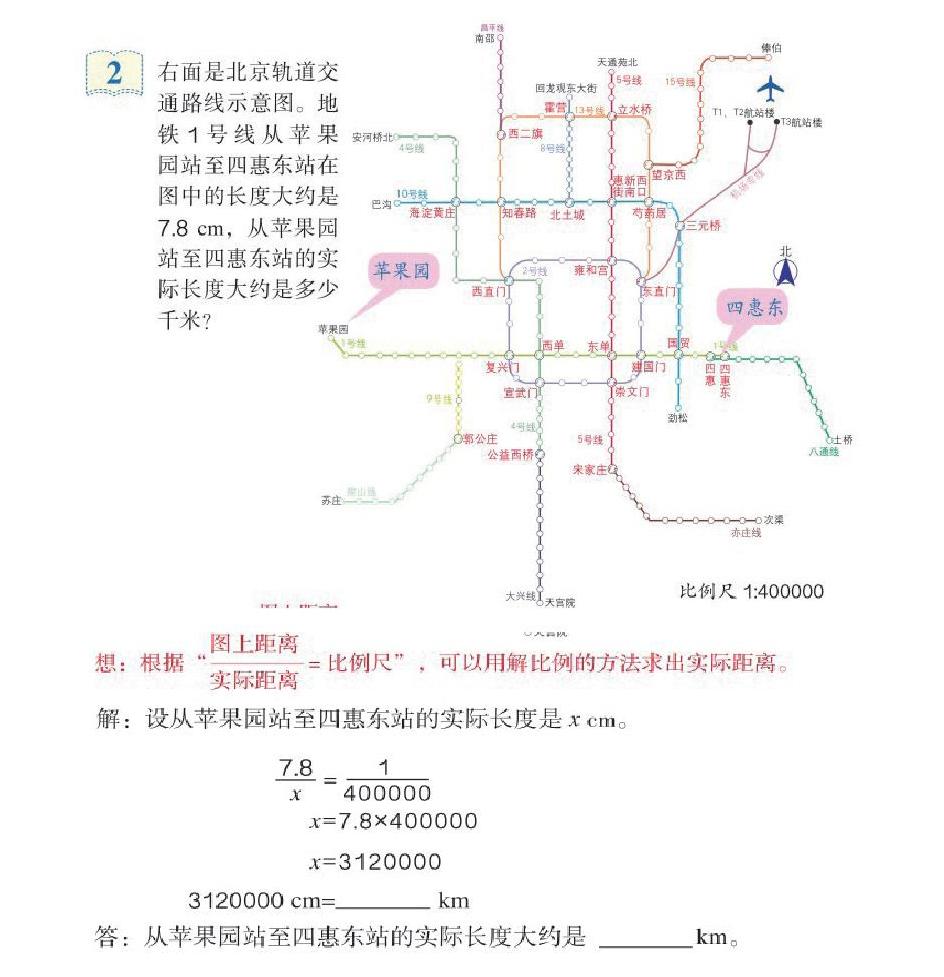
《比例尺的应用》是人教版数学六年级下册第四单元的教学内容，教材第54页呈现了如下的例题，教材还提供了解题的思路与方法。

从以往教学情况来看，学生会效仿书本提供的方法，根据比例尺的含义——“图上距离：实际距离=比例尺”进行解比例。按照教材呈现方式进行教学，原理学生容易理解，方法也容易掌握，但学生往往容易出现如下的问题：一是计算错误。对于数值比例尺，形如1：60000000，往往图上1cm代表实际距离过大，导致学生在计算实际距离时，容易出现多“0”或少“0”的现象。二是解决问题的方法单一，难与已学的内容建构联系。学生难以在解答问题时联系数值比例尺与线段比例尺的关系，不会根据题目的要求灵活选择方法进行解答。究其原因，一方面学生运算能力需加强，另一方面教材“提示”过多，限制了学生运用多样计算方法的能力。如果教师没有及时引导学生对前后知识进行有效的沟通与联系，学生解答问题的思路与方式势必局限在课时的内容，没有整体的观念，自然就没有算法的多样、思维的灵活，也就很难帮助学生走出解答“比例尺的应用”问题时的怪象——算法正确，就是难对。

一、沟通联系，找准经验的生长点

数学活动经验的积累必须基于学生原有的经验。学生学习这一内容的困惑还体现在前一课时的学习中。比例尺有数值比例尺和线段比例尺两种形式，而在本教学内容的学习中，教材按照数值比例尺的含义进行解比例，单位统一为厘米，题目经常要学生求实际距离是几米或几千米？例如“1：60000000的比例上，图上距离3厘米代表实际距离多少千米？”也就是在计算出结果后，还需要进行单位的转换，给学生计算带来一定的麻烦。既然比例尺有数值比例尺和线段比例尺两种形式，数值比例尺计算比较麻烦，能不能用线段比例尺的方法进行计算？在例题教学时，还有学生出现这样的方法“解：设两地的实际距离为x千米，列式：7.8：x=1：4，得出x=31.2。”学生这种做法是不是巧合？符合比例尺的含义吗？如果不是巧合，那它的依据又是什么？因此，教学本课内容时，除了加强学生运算能力的培养，有必要引导学生沟通数值比例尺、线段比例尺之间的联系，并让学生学会辩证地看待比例尺与比、除法之间的关系，从而找准新经验的生长点，促进学生已有经验和新的学习内容之间的沟通转化，达到自主建构的目的。

二、巧设冲突，找准经验的转换点

学生已积累的数学活动经验有时能帮助学生对新知识的学习，有时也会对新知识的学习产生负迁移作用。教师要在新旧经验的冲突与迁移中，促进已积累的数学活动经验进行一步深化与发展，形成新的经验，充实原有知识结构。结合“比例尺的应用”教学，作以实践。

师：刚刚大家读了题，下面请同学们动手试一试？

生1：解：设从苹果园站至四惠东站的实际距离是xcm。

x=7.8×400000

x=3120000

3120000cm=31.2km。

师：同意他做法的同学请举手？

师：看来，大多数同学都是用这种方式进行计算的。请大家想想，联系到以前所学的知识，还有不同的方法吗？

生2：题目告诉我们比例尺是1：400000，说明实际距离是图上距离的400000倍，当图上距离为7.8cm时，图上距离就是7.8个400000，因此图上距离为7.8×400000=3120000（cm）=31.2km。

生3：比例尺是1：400000，把图上距离当作比的前项是1份，图上距离有400000份。每份长：7.8÷1=7.8（cm），实际距离有400000份，因此长：7.8×400000=3120000cm=31.2km。

生4：图上距离：实际距离=比例尺，知道了图上距离是7.8cm、比例尺是，比号相当于除号，因此用图上距离除以比例尺就可以算出实际距离，

7.8÷  =7.8×400000=3120000（cm）=31.2km。

师：大家不仅运用了今天所学的知识，还把比例尺与按比例分配、比与除法的关系、比与倍数的关系都联系上了，非常好。请大家观察：上面的几种方法有相同的地方吗？

生5：都有7.8×400000。

师：是偶然吗？

生6：无论哪一种表示方式，都是要表示实际距离是图上的400000倍。因此，会要用7.8×400000。

师：看来大家在不同算法的背后，找到了相同的本质，所谓“殊途同归”就是这个意思。大家想一想，上堂课在学习比例尺的时候，我们学习了数值比例尺与线段比例尺。我们再来看看第一种方法？

生7：是用数值比例尺的含义，用解比例的方法进行运算的。

师：很好，如果从上述的做法中能不能得到什么启发，还有别的计算方法呢？（学生讨论）

生8：刚刚老师提醒我们比例尺有数值比例尺与线段比例尺，图上距离400000cm转换成4km，线段比例尺就是图上1cm代表实际距离4km，那么图上7.8cm就有7.8个4km，也就是实际距离是：7.8×4=31.2（km）。

生9：我们小组也是先把图上距离400000cm转化成4km，线段比例尺就是图上1cm代表实际距离4km，就可以用解比例的方法进行思考。解：设从苹果园站至四惠东站的实际距离是xkm。     ，x=7.8×4，x=31.2。

生10：我们不同意你们（生9）的做法，在上一课时化简比例尺的时候，要求单位统一，但是你们没有统一单位，图上距离单位为cm，实际距离单位为km。是不是巧合？

师：问得很好。虽然答案是正确的，这种做法会不会是一种巧合？

生9：不是巧合。我们只是用了线段比例尺的知识，用了解比例的形式。图上1cm代表实际距离4km，那图上7.8cm代表实际距离多少km，都是同一图中，比值是不变的，因此用解比例的方法进行计算。

生11：哦！明白了，两种方法（生9、生10）都是用线段比例尺的方法进行计算。也就是1cm代表4km，7.8cm就有7.8个4km。

师：看来大家已经找到两种方法相同的本质是一致的。在解答此类问题中，我们要善于联系以前所学的知识，灵活地选择方法进行计算。

……

在这一教学过程中，教师有意让不同学生的解决方法进行充分地汇报，巧妙的一问“这种做法会不会是一种巧合？”制造认知冲突，再让学生进行充分的讨论，从而丰富知识建构与完善的体验过程，使学生对新旧知识迁移有了深刻的认识，在此基础形成的新的数学活动经验。

三、破构重建，找准经验的深化点

在后续的练习中发现，学生的正确率明显比以往提高;计算的方法也多样，不再局限于用数值比例尺的方式进行解比例，会依据题目的要求把数值比例尺中图上距离转化成题目的要求（米或千米）进行计算。可知，通過课中的多种算法的呈现与比对，让学生对比例尺数值比例尺与线段比例尺的转化、比的含义、与除法的关系进行有效的梳理与联系，学生对比例尺应用的知识理解更为透彻。此次教学也为学生后续学习利用比例尺解决实际问题（作图）埋下伏笔，为学生学习下一课时打好基础。

以本课的教学为例，按照书本呈现的进行教学，不利于学生思维的发散以及对知识的整合与联系，零散、单一课时方法的掌握，还容易造成学生学习的负担。在教学中，教师应该在读懂教材的基础上，适当的跳出教材教学，不囿于教材所呈现的方法，跳出课时教学，思考本课知识在整个小学阶段知识中的联系，有利于学生对知识之间的联系理解更为清晰，减少学生对知识的记忆的负担。放眼小学阶段知识之间的内在逻辑与联系，构建前后知识之间的联系。关注课时教学，但不局限在课时的教学，有利于学生更好地掌握和理解知识，从而提升学生综合运用知识解决问题的能力。