试论数学之美

夏国海 柳 瑛

（重庆市巫山大昌中学校 重庆巫山 404700）

一、对称美

作为美学中的不变的基本法则之一——对称美，在数学之中，数学的美同样也体现在它的对称性，例如我们熟知的轴对称图形和中心对称图形，其中的对称性和平衡性，让我们直观的感受到数学图形的对称魅力。诚然，不是任何人都喜欢对称美，但在数学中，能给人心情愉悦的感觉的美，往往都是朴实无华的对称。就如数学中常见的一些概念：奇数对偶数，曲线对直线，正比例与反比例等等概念，无一不充分的显示出对称在数学中的稳定、和谐、平衡之美。

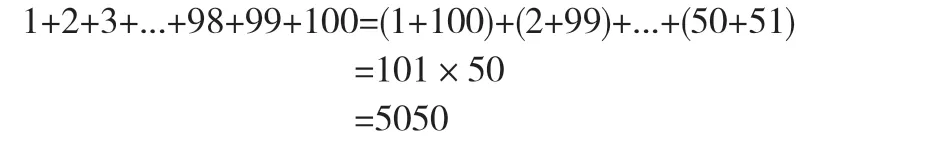
在数学上有这么一个被传颂至今的佳话，运用构思巧妙以及简捷方法的解题思路，这就是人们熟知的高斯问题：通过简简单单的数字之间结合，方便快捷的运算出数据结果，并且给人一种赏心悦目的既视感，这无疑是一种美的享受。

又如这样一个公式：

只是一串从1-9的数字，当用简简单单的运算法则将其联系到一起时，无论是数字还是运算过程，一切都是显得那么工整对称，不仅令人赏心悦目，而且美妙绝伦！

二、和谐美

因为按照黄金分割比例制造出来的事物十分和谐美丽，所以人们也把黄金分割叫作中外比。

黄金矩形的本质是通过黄金分割数设计出来的平面矩形。首先假设一个两边之比为1:∮的矩形，再由这个矩形的最短边为边，在原矩形内部做一个正方形，剩下的矩形部分两边之比仍是1:∮，这样的过程可以无限进行。这种矩形就称为黄金矩形。而1:∮的比值就是黄金分割数。欧几里得曾构造黄金矩形：

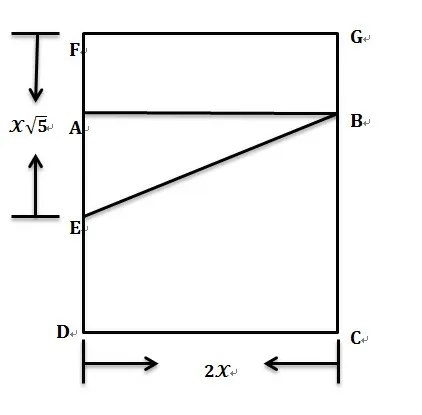
图1

延长EA于点F，使得EF=BE=，延长DB于点G使得GF||AB，得到矩形CDGF，则有

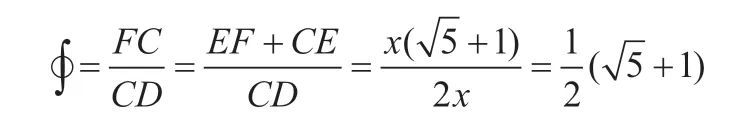
∮的导数正好就是黄金分割数。

数学中的和谐美并不只是在数学领域中才显得美丽，在我们的日常生活中也是随处可见的，例如人们的膝盖骨居然是大腿与小腿的黄金分割点；许多名画的主题都是提在整个画面的618:1000处……在日常生活中对于黄金分割的运用十分广泛，不仅仅只有黄金分割在实际生活中运用广泛，还有许许多多数学公式、运算法则等都在日常生活中有着相当重要的作用。

三、奇异美

奇异性是数学的一个基本属性。普遍地说，奇异美是很新颖的，有种出人意料的意味。在数学中有许多被称为很奇异的东西（如数学中的公式定理、方法等），引起了许许多多的赞叹和诧异。

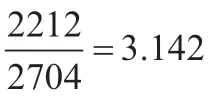
数学中关于奇异美的案例多不胜数，其中最为典型的莫过于欧拉求自然数平方的倒数之和了，他运用类比的方法解决出这个令贝努利头疼万分的无穷级数和的问题

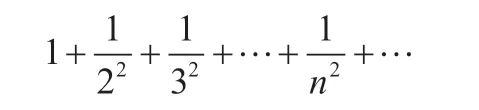
对于这个令人头疼的无穷级数问题，欧拉用发散性思维将这个问题进行三角代换，然后用三角函数和代数的方程进行解答，欧拉运用类比的方法，极其完美的解答出答案。这是欧拉在数学研究中第一次使用类比法，虽然并不严格，但为数学的另类解题思路具有启发性作用。

我们学习的过程若是细心就可以很容易找到数学的奇异美，对于一个问题始终无法用传统的方法解决时，不妨试试换个角度换个思维，往往能带来不一样的效果。

四、结束语

数学美学是对于数学进行审美活动的一种科学，数学审美无处不在，它不仅是数学家在数学创造的过程中被发现，更存在于对数学的学习与传授过程之中。数学之美不是一个笼统的概念，它具有客观的丰富的内容，对于数学美学的讨论不能只停留在口头上的感慨，而是应该用数学的观点去探究分析数学内容，这才是数学之美研究的重点。数学之美多种多样，发现数学之美需要我们在学习数学的过程，仔细品味其中的魅力。